四参数2×n 阶LC 矩形网络电特性的研究

罗礼进，陈蜀媛，罗烽华，谭志中

(1.南通大学理学院，江苏 南通 226019；2.防城港市城市建设投资有限责任公司，广西 防城港538001 3.广西大学资源环境与材料学院，广西 南宁 530004)

0 引言

在科学研究及工程技术领域，许多实际问题可以通过构建电阻网络模型进行模拟研究[1-7]，这已成为一系列科学问题研究的基本方法。随着电阻网络研究的发展，研究者已经建立了研究电阻网络的数个主要方法，如格林函数技术方法[1]、拉普拉斯矩阵方法[2]、等效变换方法[3]、递归—变换方法[4-7]等。其中的递归-变换方法具有更广泛的适用性，可适用于研究含有任意边界的有限和无限的电阻网络问题,弥补以往方法的不足[4-7]。

矩形电阻网络问题一直是电阻网络研究关注的热点之一，近年来取得较大进展，尤其在少参数（一个或两个）电阻网络问题得到了比较好的解决，如含有2参数的m×n阶矩形电阻网络的等效电阻问题[6]。在多参数电阻网络问题的研究上也取得一定的进展，如含有3参数的2×n阶纯电阻网络的等效电阻问题[5]。在复阻抗网络研究方面，少参数复阻抗网络的研究取得了一定的进展[7]，但在多参数复阻抗网络方面少有研究。本文将以含有4参数的2×n阶LC矩形网络为例，研究多参数的复阻抗网络模型的等效复阻抗问题。

1 四参数2×n 阶LC 矩形网络的研究

我们称图1为一类含有4参数的2×n阶LC矩形网络模型，该模型包含有4个电路参数Ca、Cb、L、L0。本文将研究a、b两节点间的等效复阻抗Z ab（n）和a、c两节点间的等效复阻抗Z ac（n）的普适公式和基本特性。为解决此问题，依据上述的递归-变换方法，分建立差分方程模型、求差分方程模型的通解、求边界电流特解、计算节点间的复阻抗四个步骤进行。下面首先求解a、b两节点间的等效复阻抗Z ab（n）。

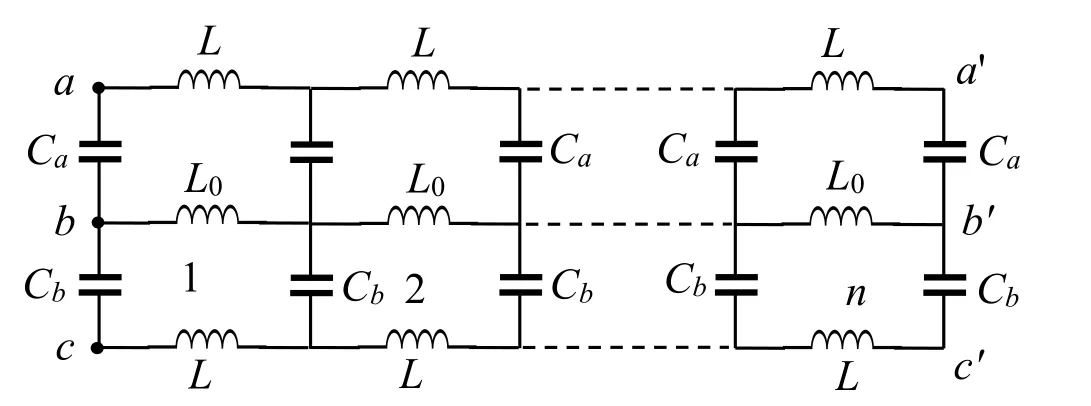
图1 含有4参数的2×n阶LC矩形复阻抗网络模型

1.1 建立差分方程模型

在图1所示的LC网络中，设输入电流的圆频率为ω，则电感L、L0的阻抗分别为z=jωL、，电容Ca、Cb的阻抗分别为，j2=-1。设电流I从a输入至b输出。不失一般性，选取图1所示网络中的任意子网络结构进行研究，如图2所示。设在第k个子网络中，水平方向的三个电感中通过的电流分别为Iak、Ibk、Ick（1≤k≤n），竖直方向的两个电容中通过的电流分别为Ik、（1≤k≤n+1）。各LC网络元中的电流方向如图2所示。

图2 子网络电流参数

在图2 的子网络中应用基尔霍夫电流定律得到节点电流方程

在图2 的子网络中应用基尔霍夫电压定律得到第k个回路的电压方程

同理得到第k-1 个回路的电压方程

取差运算，分别由式（4）-（6）和（5）-（7）得到

将式（1）、（2）、（3）分别代入（8）、（9）化简整理得

为便于研究，将方程（10）、（11）写成矩阵形式

方程（12）就是本文推导出的关键的差分方程模型，但是如何求解该方程是解决问题的关键。如果用传统的方法求解该方程是很困难的事情，本文将采用矩阵变换的方法解决该问题。

1.2 求差分方程模型的通解

为了求解差分方程（12）的通解，根据文献[3]的解法，先通过矩阵变换，将矩阵方程（12）变换为一个简单的矩阵方程，然后求此简单矩阵方程的特征方程的特征根，最后由特征根求出矩阵方程（12）的通解。

将方程（12）中Ik、的系数矩阵左乘一个二阶矩阵A，使得

其中设待定的二阶矩阵A为

并且其中λ1、λ2和t1、t2均为待定系数。将式（13）展开并且根据式（13）的矩阵左右相等得

把（16）代入（15）消去t得到

将矩阵方程（12）两边左乘矩阵A变换为如下成简单的方程

其中k=1,2,3……，且

由矩阵方程式（20）得差分矩阵方程的特征方程

设关于x的方程的两根分别为α、β，关于y的方程的两根分别为γ、δ，解（22）得到

根据文献[3]的解法，方程（20）的解为

1.3 求边界电流的特解

当电流从a输入至b输出时，根据电流的连续性方程由图3 可得

图3 边界网络电流参数

将式（25）分别对k从1 到n+1 求和并应用式（26）得

根据文献[3]的分析方法，由图3 得到边界电流参数方程

将方程（29）两边左乘一个前文已经求出的二阶矩阵A，并且应用式（18）、（19）的关系化简整理得

将式（31）分别代入式（27）、（28）化简整理得

第二，教学点逐步健全档案，完善制度。中心校的规章制度在教学点上墙，且各种计划及作息要和中心校要求保持一致。

式（32）、（33）即为4 参数2×n阶LC矩形网络中左边界的电流特解。

1.4 求等效复阻抗

又由图3 可知：Uab=I1za，根据欧姆定律

把式（34）代入（35）得到

其中α、β和γ、δ分别由式（23）、（24）确定。式（36）即为a、b二节点间的等效复阻抗Z ab（n）的普适公式。

用同样的方法可计算出a、c两节点间的等效复阻抗Z ac（n）。

其中α、β和γ、δ分别由式（23）、（24）确定，t1、t2由式（19）确定，。式（37）即为a、c二点间的等效复阻抗Z ac(n)的通项表达式。

2 等效复阻抗特性的讨论

特征方程（22）的判别式分别为

将（19）代入（23）、（24）得到

2.1 情形1：ω ＞（q ＞ 0）

当ω＞2q时，有 Δ1＞ 0，Δ2＞ 0。此时，α、β、γ、δ分别如（40）、（41）所示，均为实数，因λ1、λ2都是实数，所以由（42）可知Z ab（n）为纯虚数。

图4 是Ca=1.2 ×10-3F、Cb=4.7 ×10-3F、L=2.6 ×10-2H、L0=7.2 ×10-2H，且n分别取1 至50 时，Z ab（n）/ j 随ω（ω∈[300,30000]）变化的三维曲线图。从图中可看出，n取不同的值时，Z ab（n）/ j 随ω的变化都有相同的趋势，即都随ω的增加单调增加，并且Z ab（n）/ j在低频区（ω∈[300,2300]）的变化梯度较大，而在高频区（ω∈[2300,∞]）的变化梯度较小。ω→∞时，Z ab（n）/ j → 0。

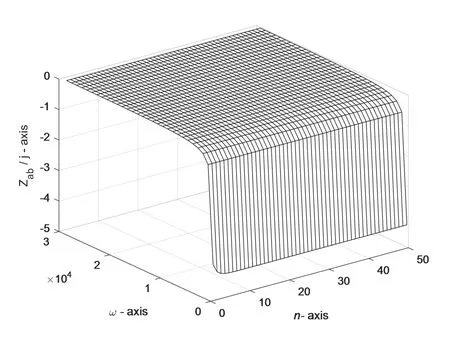
图4 Z ab（n）/ j 随ω（ω ∈[300,30000]）和n(n∈[1,50])变化的三维曲线图

2.2 情形2：ω=（q ＞ 0）

此时，Z ab（n）也为纯虚数。

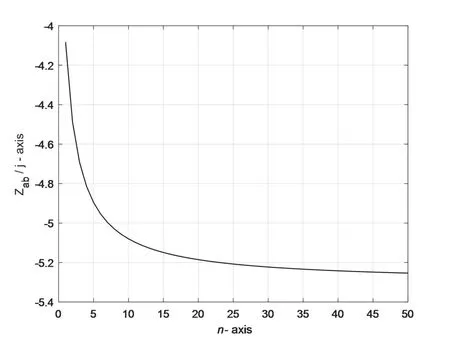
图5 ω=时 Z ab（n）/ j 随n(n∈[1,50])变化的曲线图

2.3 情形3：（p ＞0、q ＞0）

将（48）代入（42）得

由此可见，Z ab（n）仍为纯虚数。

图6 是Ca=1.2 ×10-3F、Cb=4.7 ×10-3F、L=2.6 ×10-2H、L0=7.2 ×10-2H，且n分别取1 至50 时，Z ab（n）/ j 随ω（ω∈[90,290]）变化的三维曲线图。从图中可看出，对应每一个n值，Z ab（n）/ j 随ω的变化不再是单调变化，而是在Z ab（n）/ j=0两则正负振荡变化。

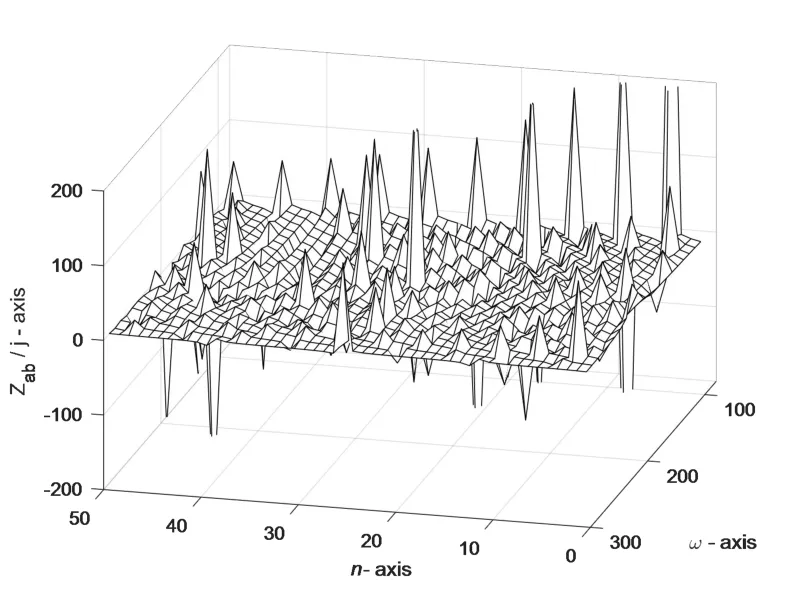
图6 Z ab（n）/ j 随ω（ω∈[90,290]）和n(n∈[1,50])变化的三维曲线图

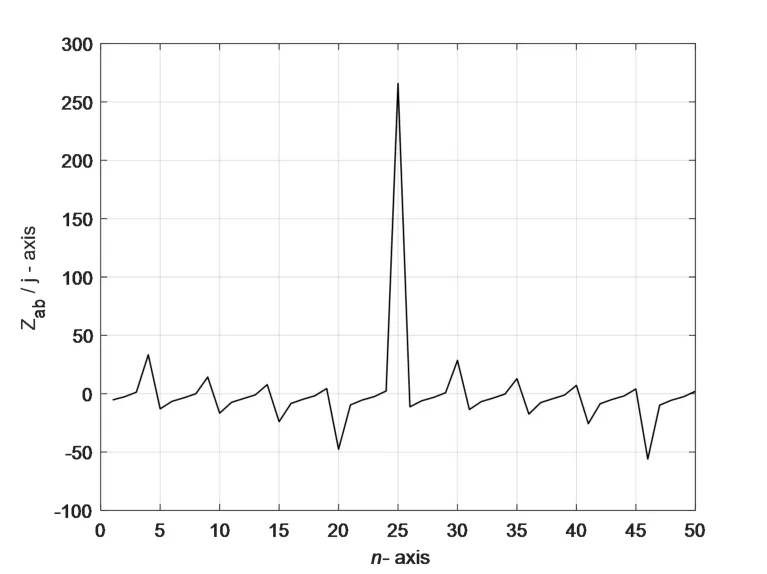
图7 ω=时 Z ab（n）/ j 随n(n∈[1,50])变化的曲线图

2.4 情形4：ω=（p ＞ 0）

而γ、δ仍为（46）、（47）所示，并有（48）的结果，所以将（48）、（51）代入（42）得

由此可见，Z ab（n）仍为纯虚数。

2.5 情形5：0＜ ω＜（p ＞ 0）

所以将（55）、（48）代入（42）得

由此可见，Z ab（n）仍为纯虚数。

图8 是Ca=1.2 ×10-3F、Cb=4.7 ×10-3F、L=2.6 ×10-2H、L0=7.2 ×10-2H，且n分别取1 至50 时，Z ab（n）/ j 随ω（ω∈[1,85]）变化的三维曲线图。从图中可看出，对应每一个n值，Z ab（n）/ j 随ω的变化是在Z ab（n）/ j=0两则正负振荡变化。

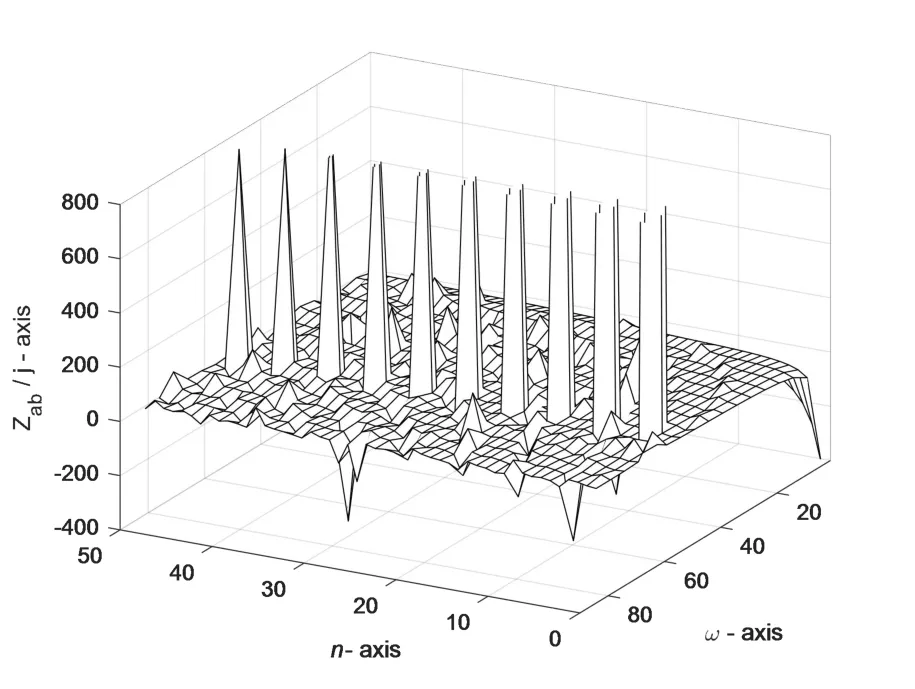
图8 Z ab（n）/ j 随ω（ω∈[1,85]）和n(n∈[1,50])变化的三维曲线图

3 总结