谈数列复习需要关注的四个问题

2022-03-31辉特级教师

高中数理化 2022年5期

关键词：项数通项关联性

张辉特级教师赵涛

(北京市陈经纶中学)

数列的特点在于数字排列的有序性和规律性,数列问题的研究是要找出数列背后本质关系.数列是特殊的函数,除了有自身的研究方法,从函数角度研究数列是高考重点考查的内容之一,内容多并且与其他知识关联性强.本文主要谈数列复习中四个值得关注的问题.

1 寻找项an 与项数n 的关系是探求数列特点的关键

1.1 归纳是寻找项an 与项数n 关系的根本方法

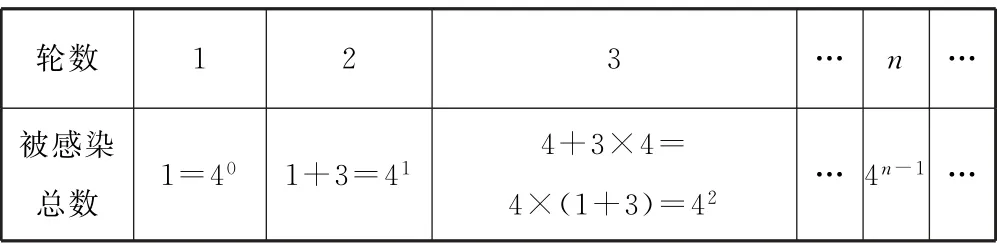
表1

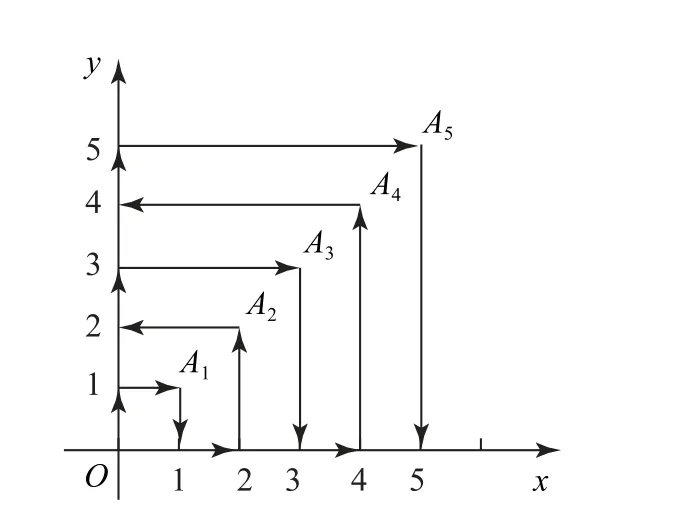
图1

表2

因为an＝n(n＋1),且44×45＝1980,所以运动了1980秒时到点A44(44,44),又由运动规律知,A1,A2,…,An中,奇数点处向下运动,偶数点处向左运动,到达A44(44,44)时,再向左运动42秒到达点(2,44),即运动2022秒这个粒子所处位置为(2,44).

上面两个例子都是通过归纳找出一般性规律,再去解决特殊问题,归纳是发现数列一般规律的重要方法.例2中,观察前后项关系由a1＝2,a2＝6,a3＝12,a4＝20,….a2－a1＝2×2,a3－a2＝2×3,a4－a3＝2×4,…,an－an－1＝2n(n≥2,n∈N*),将以上各式相加有an－a1＝2×(2＋3＋4＋…＋n),所以an＝n(n＋1).

1.2 递推是寻找项an 与项数n 关系的常用方法

解决数列问题时,有时也可以找到前后项的关系,利用它们的关系求出数列的特殊项,有时甚至能求出数列的通项公式.例2点评中就是利用递推关系求数列通项公式的累加法.这种方法源于课本等差数列通项公式的推导,课本中推导等比数列通项公式所采用的方法是累乘法.

例3 正整数按如图2所示的形式排列,位于对角线位置的正整数1,3,7,13,…构成数列{an},则a7＝_________,通项公式an＝_________.

图2

2 运用函数思想分析项an(前n 项和Sn)与项数n 的关系是解决数列问题的有效路径

数列是一种特殊的函数,等差(比)数列的通项公式以及前n项和公式都可以看作是特殊的函数,所以借助数列的复习可以再一次学习和体会函数思想在解题中的作用.

例5 数列{an}的通项公式为an＝n2＋kn＋2,且满足a1＜a2＜a3＜…＜an＜an＋1＜…,求实数k的取值范围.

当4n－34＝0时,n＝8.5,即当n≤8时,an＜0;n＞8时,an＞0,所以Sn的最小值为S8,即当n＝8时Sn取得最小值.

3 明确Sn 与an 的关系,重视求和时的分类与整合思想

数列{an}的前n项和为Sn＝a1＋a2＋a3＋…＋an,其中S1＝a1,S2＝a1＋a2,S3＝a1＋a2＋a3,….任给一个n,都有唯一的Sn与之对应,所以Sn是n的函数,{Sn}也是数列,其中a1＝S1,a2＝S2－S1,a3＝S3－S2,…,an＝Sn－Sn－1.所以,an＝Sn－Sn－1是在n≥2,n∈N*的条件下才能成立的.

例8 已知等差数列{an}的首项a1＝1,公差d＞0,且第2 项、第5 项、第14 项分别为等比数列{bn}的第2项、第3项、第4项.

(1)求数列{an}与{bn}的通项公式;