关于指数丢番图方程(an-1)((a+s)n-1)=x2可解性的研究

罗永亮,杨海,李恒

(西安工程大学理学院,陕西 西安 710048)

1 引言及结论

设Z,N∗分别表示全体整数和正整数的集合,且a,b均是大于1的正整数,近些年来,对方程

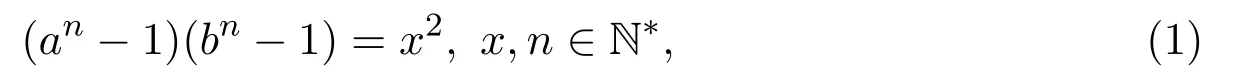
正整数解的讨论是一类很具有研究价值的指数丢番图问题,数论及其相关领域中有关数列的平方类等问题都可以转化为该方程的求解.

当s=1时,文献 [1]证明了:当a=2时,方程 (an−1)((a+1)n−1)=x2无正整数解(n,x).文献[2]证明了:当a=3时,方程(an−1)((a+1)n−1)=x2无正整数解(n,x).文献[3]对此进行推广,证明更具有一般性的以下结果:当a≡2,3(mod 4)时,方程(an−1)((a+1)n−1)=x2无正整数解(n,x).并给出对于任何大于1的正整数,方程(an−1)((a+1)n−1)=x2无正整数解(n,x)的猜想.

文献[4-10]对相关问题进行了深入的探究,并给出了许多很有价值的结论和研究方法.此外,文献[11-15]从不同角度对a,b的限定条件和方程中的常量进一步拓展,得出了一些具有创新性的结论,这些都为推动解决这一类指数丢番图指数方程做出了贡献.

本文将运用初等数论中的一些方法技巧,并与现有结论相结合,得出了更具有一般性的结果.

定理1.1设a,n,s,x∈N∗,当s≡1(mod 2),n≡0(mod 2),1≤s≤a,n>1时,则方程(2)没有正整数解.

定理 1.2设a,n,s,x∈N∗,当n≡s≡1(mod 2),n>1时,则对于以下三种情况:(i)a≡0(mod 4),s≡3,7(mod 8);(ii)a≡2(mod 4),s≡1(mod 4);(iii)a≡3(mod 4),其中任意一种成立时,方程(2)无正整数解(n,x).

定理 1.3设a,n,s,x∈N∗,当n≡s≡1(mod 2)时,则对于以下两种情况:(i)当a≡1(mod 2)时,且 (a−1)|x;(ii)当a≡0(mod 2)时,且 (a+s−1)|x,其中任意一种成立时,方程(2)无正整数解(n,x).

看何东快被逼休克了，何西何北只好把他拉到一边，他们俩对他为什么不结心里有数，现在只想知道这人活过来了，何东下一步准备怎么办。

显然,文献[1-3]的结论可由定理1.1和定理1.2推导得出,而且进一步给出了拓展的结果.总之,上述三个定理给出了判定方程(2)的正整数解(n,x)不存在的充分条件,将方程(2)有正整数解的范围进一步缩小,并提出了以下猜想.

猜想 1.1当1≤s≤a,s≡0(mod 2),n>1时,方程(2)只有有限个正整数解(n,x).

2 引理

引理 2.1[4]方程

无正整数解(n,X,Y).

引理 2.2[3]设d是非平方正整数,(u1,v1)是Pell方程u2−dv2=1,u,v∈N∗的最小解,则(uk,vk)满足,是该Pell方程全部解,并且满足以下结论:(i)当 2k时,u1|uk;(ii)当 2|uk时,有 2k以及 2|u1;(iii)当 2|u1时,如果 2uk,则必有

引理 2.3[2]丢番图方程(an−1)(bn−1)=x2,x,n∈N∗在n≡1(mod 2)条件下,如果v(a−1)和v(b−1)具有相反的奇偶性,则该丢番图方程没有正整数解(n,x).其中v(a−1),v(b−1)分别表示a−1,b−1的质因数分解中2的次数.

3 定理证明

3.1 定理 1.1的证明

3.2 定理 1.2的证明

定理1.2可分以下三种情况证明.

当a≡0(mod 4),s≡3,7(mod 8)时,可设a=4t1,s=8t2+3或8t2+7,则在方程(an−1)((a+s)n−1)=x2,x,n∈N∗中,可得

v(a−1)=v(4t1−1)=0,v(a+s−1)=v(4t1+8t2+2)=v(4t1+8t2+6)=1.

因此v(a−1)和v(a+s−1)具有相反的奇偶性.根据引理2.3可知,方程(2)在满足定理条件(i)时,没有正整数解(n,x).

当a≡2(mod 4),s≡1(mod 4)时,可设a=4t1+2,s=4t2+1,则在方程(an−1)((a+s)n−1)=x2,x,n∈N∗中,可得

v(a−1)=v(4t1+1)=0,v(a+s−1)=v(4t1+4t2+2)=1.

因此v(a−1)和v(a+s−1)具有相反的奇偶性.根据引理2.3可知,方程(2)在满足定理条件(ii)时,没有正整数解(n,x).

当a≡3(mod 4)时,由s为奇数,则可设a=4t1+3,s=2t2+1,则在方程(an−1)((a+s)n−1)=x2,x,n∈N∗中,可得

v(a−1)=v(4t1+2)=1,v(a+s−1)=v(4t1+2t2+3)=0.

因此v(a−1)和v(a+s−1)具有相反的奇偶性.根据引理2.3可知,方程(2)在满足定理条件(iii)时,没有正整数解(n,x).

定理1.2得证.

3.3 定理 1.3的证明

定理1.3可分以下两种情况证明.

情形1:设a,n,s,x∈N∗,s≡n=1(mod 2),从方程(2)可得

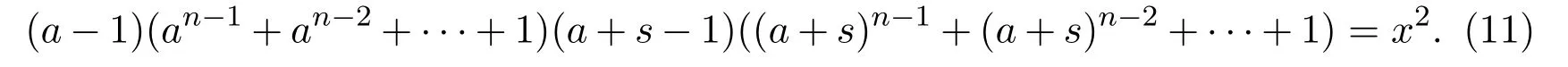
如果(a−1)|x,则(a−1)2|x2,从而可得

显然易得ns((1+s)n-1+(1+s)n-2+···+1)是奇数.而当a≡1(mod 2)时,a−1为偶数.因此(13)式不可能成立,得出矛盾.此时方程(2)无正整数解(n,x).

情形2:设a,n,s,x∈N∗,s≡n=1(mod 2),从方程(2)可得

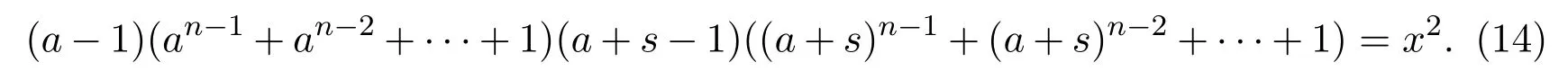
如果(a+s−1)|x,则(a+s−1)2|x2,从而可得

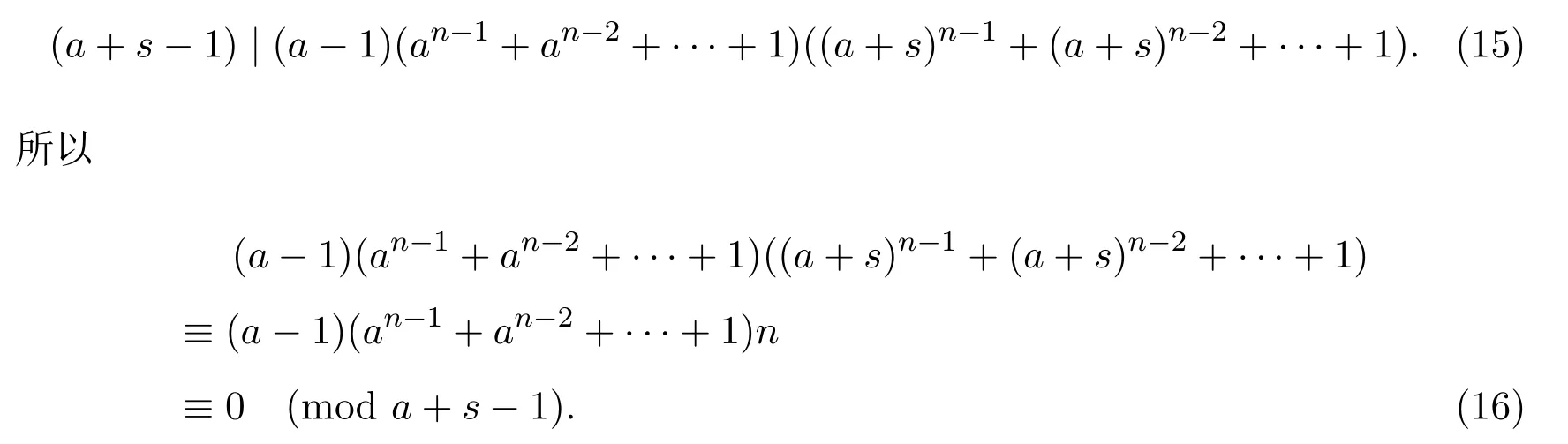
显然当a≡0(mod 2)时,易得(a−1)(an-1+an-2+···+1)是奇数.a+s−1为偶数.因此(15)式不可能成立,得出矛盾.此时方程(2)无正整数解(n,x).

定理1.3得证.

4 结束语

众所周知,缩小解的范围是丢番图方程研究方法的重要内容之一,本文运用初等数论的方法和技巧,得到了当a,b在给定条件下,方程(an−1)(bn−1)=x2没有正整数解,三个定理的结果很大程度的缩小了判定方程可解性的范围.文中的研究方法可以进一步拓展应用到此类型的方程求解中,在今后的工作中,仍将继续致力于这类指数丢番图方程求解的研究与推广.