带有对数非线性源的p-Kirchhoff方程解的整体存在性和衰减估计
2022-03-31杨雨杨晗
杨雨,杨晗
(西南交通大学数学学院,四川 成都 611756)
1 引言
本文考虑如下带有对数非线性源的p-Kirchhoff方程的初边值问题
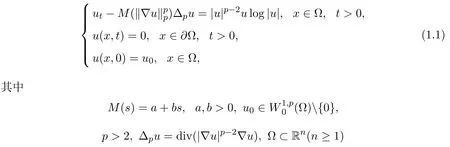
是具有光滑边界∂Ω的有界区域.
近年来,关于具有不同非局部项的偏微分方程的研究越来越多,由于它在物理学和生物学上的重要作用,吸引了许多学者的注意.例如,文献[1]介绍了如下的具有非局部系数的双曲线方程

它在有限域Ω⊂Rn中就是一个关于在均匀密度ε下弹性字符串小阻尼横向摆动的模型.通过令ε=0,得到如下的p-Kirchhoff抛物方程

这类方程的特点就是系数 Δpuε或 Δpu依赖于未知函数u的梯度,即方程不再是点态恒等式.由于这类模型是由Kirchhoff(基尔霍夫)首次提出的,故将这类方程称为p-Kirchhoff方程或非局部方程,当p=2时,简称为Kirchhoff方程.关于非局部的其他理由是基于这样一个事实:测量不是点态的,而是通过一些平均量得到的.
尽管Kirchhoff方程已经被提出很长一段时间了,但是在基于文献[2]之后,它的解的存在性,唯一性,正则性等性质才得到了很好的研究.例如,关于上述方程的椭圆对应方程
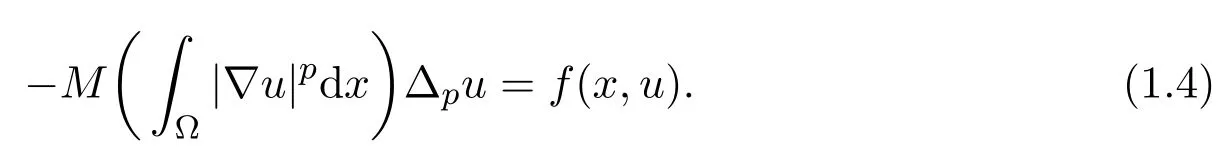
当p=2时,文献 [3]利用最小化参数和变分法研究了方程 (1.4)正解的存在性.文献 [4]利用截断参数和先验估计研究了在M(s)是一个非增函数并且f(x,u)满足Ambrosetti-Rabinowitz条件时,方程(1.4)的正解的存在性,关于此方程的更多研究可见文献[5-9].
与Kirchhoff方程有关的研究还有很多.例如,文献[10-11]研究了当p=2并且扩散系数M(s)满足:对所有的s≥0,有
0 以及源项f(x,t,u)≡f(x)时,方程(1.3)的解的存在性,唯一性以及强解或弱解的渐近形态等问题.随后文献[12]将结果扩展到p-Kirchhoff方程中.文献[13]利用修正势井以及变分法研究了方程(1.3)在p=2,M(s)=a+bs,a,b>0,以及f(x,t,u)=|u|q-1u,q∈(3,2∗−1]的条件下,关于不同初值条件的解的整体存在性,衰减估计以及有限时间爆破.文献[14]扩展了文献[13]的结果,研究了如下的p-Kirchhoff方程 得到了其在一般非线性项的条件下解的有限时间爆破. 文献[15-16]中通过势井理论研究了对数源问题后,对数非线性源便成了当下非线性发展方程的热点.文献[15]研究了如下具有对数非线性源的抛物方程的初边值问题 其中 Ω⊂Rn(n≥1)是一个具有光滑边界∂Ω的有界区域.利用势井理论,他们在J(u0) 文献[17]中研究了如下带有对数非线性源的拟线性扩散方程 其中φp(u)=|u|p-2u,得到了在J(u0) 从上述文献可知,关于带一般非线性源的p-Kirchhoff方程的研究已经逐渐成熟,但带对数非线性源的p-Kirchhoff方程的研究结果还较少.基于此,本文拟在文献[14]和文献[17]的启发下:研究一类带有对数非线性源的p-Kirchhoff方程的初边值问题,讨论当初值满足不同条件时,其解的整体存在性以及衰减估计. 本节中首先给出文中会用到的符号. 首先构造问题(1.1)的局部解,再以此证明当初值属于W+时,问题(1.1)的全局弱解的存在性.最后进一步得到‖u(t)‖2的衰减估计.为了得到衰减估计,需利用下面的引理.


2 预备知识及引理
2.1 符号和不等式
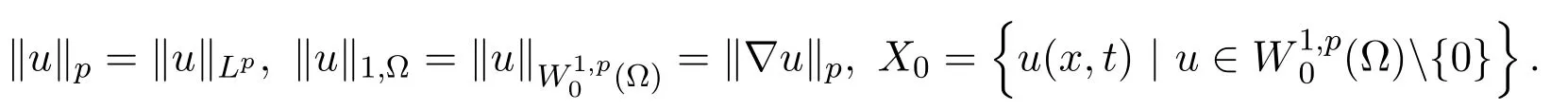

2.2 势井以及相关引理


3 整体解和衰减估计










