三维数字图像相关法在带孔洞试件力学行为研究中的应用
2022-03-31喻苏婷
喻苏婷,蒋 明
(苏州科技大学 土木工程学院,江苏 苏州 215011)
在实际工程用中,由于日常使用和制作工艺的原因,材料总会存在一定的瑕疵,这些瑕疵与孔洞会对构件的承载能力及变形产生一定的影响,因此,为了提高工程寿命,优化工程结构,研究孔洞边缘区域的应变集中现象至关重要。吴晓等人[1]采用弹性理论研究了不同弹性模量薄板上圆孔的孔边应力集中问题;谭林等人[2]研究了板宽与圆孔边应力集中程度的关系;Hoang等人[3]利用复变函数法分析了孔边应力分布;王岩等人[4]确定了含椭圆孔的有限大矩形板在承受拉伸和剪切载荷时的应力分布。目前常用粘贴应变片和数值模拟的方式来分析孔洞周围区域的应变。由于受到应变片尺寸及数量的限制,采用应变片测量无法获得完整的孔洞边缘区域应变分布。数值模拟虽然可以模拟全场应变,但和实验结果有一定的误差。Sutton等人[5-6]学者提出的三维数字图像相关法,具有非接触性、全场高精度等优点。运用此方法可精确测得试件在一个完整的拉伸过程中孔洞边缘区域表面的全场应变。陈亚军等人[7]探讨了三维数字图像相关技术在材料形变研究中的应用。杨立云等人[8]运用三维数字图像相关法研究了圆孔在拉应力下的力学行为。笔者研究基于三维图像相关技术,测量分析了带椭圆形孔洞和菱形孔洞在拉伸试验下,孔洞周边的应变分布及不同高宽比对孔边应变集中的影响。
1 三维数字图像相关法原理
三维数字图像相关法是基于计算机双目立体视觉原理和数字图像相关匹配技术的三维变形测量方法。如图1所示,由两个互成一定角度的相机同步拍摄被测物表面,通过分析左右相机记录的散斑图像,运用图像相关运算获得以被测点为中心的图像子区在左右图像中对应的位置,根据相机标定获得的左右相机的内外参数,建立空间几何关系,从而实现试件表面的三维重建[9-10]。

图1 三维数字图像相关原理图

式中,m为图像子区域半宽;f(x,y)、g(x′,y′)分别为参考图像子区域变形前后的灰度值;fm、gm分别为参考图像子区域变形前后的灰度平均值,即有
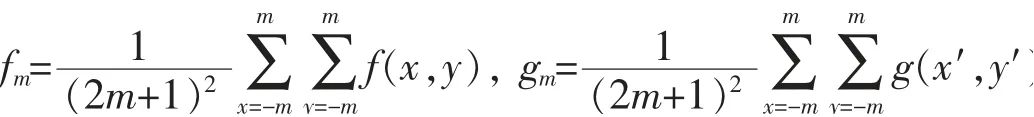
2 试验及结果分析
选取工程中经常使用的304钢板作为试件材质,屈服强度Rp0.2=289 MPa,抗拉强度Rb=945 MPa。弹性模量E=193 GPa,泊松比ν=0.3。设计板厚2 mm,宽度12.5 mm,平行段长度45 mm,原始标距为30 mm。试件中心开孔,孔洞宽度b=3 mm,高度h分别为1.5 mm、3 mm、6 mm,菱形孔洞试件按照孔洞高度从小到大依次编号为D1-D3;同样椭圆形孔洞试件为E1-E3。试件尺寸及孔洞形状如图2示。
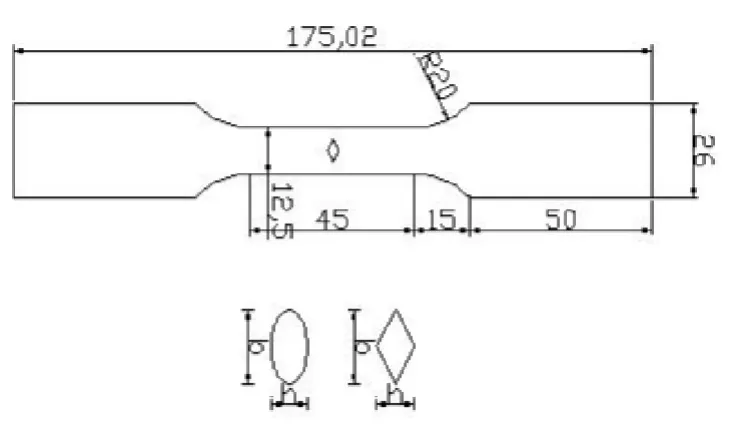
图2 结构尺寸图
实验装置包括拉伸试验机、两个工业相机、两个50 mm镜头、光源及控制系统,其中相机分辨率参数为550万像素,物像倍率为0.14,图像相关计算精度为0.03。图3为实验现场。加载模式参照规范《GB/T 228.1-2010金属材料拉伸实验第1部分:室温实验方法》。试验过程中采用PCIE8620数据采集卡同步控制试验机力传感器[11],实现CCD图像与力值数据的同步采集。每采集一组图像记为一个stage,记录的第一组图像记为stage0。每个stage对应一个力值数据。

图3 实验环境图
2.1 拉伸状态下孔边应变分析
图4给出了试件在拉伸过程中荷载分别为4 kN、10 kN、12 kN时,试件表面的纵向应变分布图及截面AB上各点的应变值。当荷载为4 kN时,材料处于弹性阶段,孔洞周围出现剪切带;荷载为10 kN时,试件处于塑性阶段,试件出现颈缩,孔洞左右两端应变集中现象明显;由于试件D1的极限荷载为12.5 kN,则取荷载为12 kN时进行分析,此时孔边应变更加集中,颈缩现象更加明显。

图4 试件在不同荷载阶段孔洞周边应变分布图
为研究应变集中的区域,观察各带孔洞试件在拉伸过程中的应变分布图可得,整个过程中各孔洞左右两端的一个扇形区域内都存在应变集中现象。取试件D1荷载为10 kN时进行分析,各孔洞的宽度都为b,在与孔边为距离为1b、2b、3b处取截面,如图5所示。计算得到同一时刻3个截面的应变曲线,如图6所示。当截面与孔边距离为b时,截面处应变分布不均匀,最大应变比最小应变大0.119。当截面与孔边距离为2b时,截面处最大应变比最小应变大0.031。当截面与孔边距离为3b时,截面处最大应变比最小应变大0.004。应变集中主要发生在与孔边距离2b范围之内,与孔边距离超过3b时,截面外各点应变受孔洞影响可忽略不计。

图5 选取截面分布图

图6 选取截面处应变曲线
为研究应变集中程度随时间的变化规律,如图7所示,取试件D1为例,在孔洞边缘区域取点1-6,在截面3b上取点7。计算分析得到各点的应变-时间曲线,如图8所示。观察D1各点的应变-时间曲线。在材料处于弹性阶段初期,各个带孔洞试件的孔边就出现应变集中现象,但孔洞左右两端的应变只略大于其他区域,应变集中程度非常小,此时点1-3的荷载与应变不再成线性关系。进入塑性阶段后,点1-7的应变迅速发展,但孔边横向的点1-3应变远大于纵向的点4-7。点1-3中越靠近孔洞的点应变越大,但纵向分布的点4-7越靠近孔洞应变越小。

图7 选点分布图

图8 D1各点的应变-时间曲线
2.2 孔洞的高宽比对孔边应变集中的影响
图9给出了在拉伸试验中不同高宽比的菱形孔洞试件,在断裂前最后一刻的应变分布图,可以明显的观察到,高宽比越大,可观察到的裂缝越短。由于孔洞的高宽比不同,孔洞周围应变集中程度也不同。取图5中的点3进行分析,得到图10所示的点3的应变-荷载曲线,可以看出试件拉伸过程中,各试件的点3在弹性阶段应变集中程度差异不大;在塑性阶段,应变曲线分散开来。在荷载条件相同时,试件D1的应变集中程度最大,试件D2的应变集中程度次之,试件D3的应变集中程度最小,见表1。菱形孔洞的高宽比越小,孔边应变集中程度越大,越容易破坏。

图9 菱形孔洞断前一刻表面应变分布图

图10 菱形孔洞点3应变-荷载图

表1 带菱形孔洞试件点3应变表
图11给出了在拉伸试验中不同椭圆形孔洞,在断裂前最后一刻试件表面的纵向应变分布图。根据图12及表2可以看出在相同荷载条件下,各试件点3的应变在弹性阶段应变集中程度差异较小,在塑性阶段初期,试件E1-E3的应变集中程度依然差异不大,随着试件的拉长曲线开始分散,在荷载为12 kN时,可以观察到试件E1的应变集中程度略大于试件E2、E3,试件E3的应变集中程度最小。在荷载为14 kN时,试件E1的应变集中程度已经明显大于试件E2、E3。椭圆形孔洞的高宽比越小,孔边的应变集中程度越大。

图11 椭圆形孔洞颈缩阶段表面应变分布图

图12 椭圆形孔洞点3应变-荷载图

表2 带椭圆形孔洞试件点3应变表
2.3 菱形与椭圆形孔边应变集中程度的对比
图13给出了孔洞高度同为1.5 mm的试件D1与试件E1上点3的应变图。在弹性阶段,试件D1与试件E1的点3应变集中程度相似,进入塑性阶段后,曲线开始分散。在塑性阶段前期,荷载为10 kN时,菱形孔洞的应变只略大于椭圆形孔洞。随着荷载的增加,菱形孔洞的应变与椭圆形孔洞的应变差越来越大,荷载为12 kN时,菱形孔洞的应变明显大于椭圆形孔洞。在荷载相同时菱形孔洞应变更加集中,极限荷载小,容易破坏。
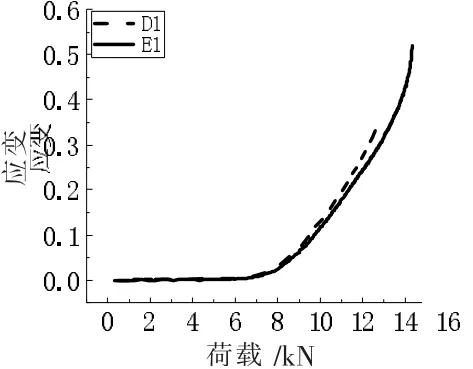
图13 试件D1、E1点3的应变-荷载图
由表3可得在高宽比相同时,带菱形孔洞试件的极限荷载小于带椭圆形孔洞试件的极限荷载。带菱形孔洞试件的极限荷载与菱形孔洞的高度有关,且极限荷载相差明显,菱形孔洞高度越小,极限荷载就越小。椭圆形孔洞的高宽比越小,其试件极限荷载也越小。试件D1与试件D3的极限荷载相差2.6 kN,试件E1与试件E3的极限荷载仅相差0.9 kN,相对于带椭圆形孔洞试件而言,孔洞的高宽比对带菱形孔洞试件的极限荷载影响更大。

表3 各带孔洞试件所能承受的极限荷载
3 结语
基于三维数字图像相关方法对带不同菱形及椭圆形孔洞试件拉伸试验进行了测量,获得了试验不同时刻带不同形状孔洞试件表面的全场应变分布;对孔洞边缘区域表面的应变规律进行分析,带不同形状孔洞试件均存在应变集中现象。
各个孔洞的应变集中主要发生在孔边2b范围之内,在孔洞左右两端呈扇形分布。在垂直于荷载的方向,越靠近孔洞,应变集中程度越大。
孔边应力集中程度受孔洞形状及高宽比影响较大。同种形状下,高宽比越小,孔边应变集中程度就更大。在相同高宽比条件下菱形孔洞应变集中程度大,极限荷载小,更容易破坏。
