基于松鼠搜索算法与IHS变换的遥感图像融合
2022-03-31阮理念
阮理念,董 燕
(昆明理工大学 国土资源工程学院,云南 昆明 650032)
随着遥感技术快速发展,人们获取了大量的遥感图像,其被广泛应用于城市规划和灾害监测等方面。为了得到信息更加丰富的图像,常采用融合技术对多光谱(multispectral,MS)和全色(panchromatic,PAN)图像进行融合。图像融合作为遥感图像预处理的重要环节,为后续的分类和变化检测等提供了重要数据保障[1]。图像融合可分为像素级、特征级和决策级3个层次。由于像素级图像融合最大程度地保留了原始信息,融合效果较好,一直是研究的热点。像素级融合方法包括IHS(intensity-hue-saturation,强度-色调-饱和度)变换[2-3]、PCA(principal component analysis,主成分分析)变换[4-5]和小波变换[6-7]等。
文中针对IHS变换的光谱失真现象进行研究,根据文献[8]提出的空间保真和光谱保真项,并结合边缘信息保持策略建立优化目标,采用一种群体智能优化算法——改进的松鼠搜索算法(improved squirrel search algorithm,ISSA)求解控制参数,经过IHS逆变换后得到融合图像,旨在使融合后的图像在保留原始空间信息的同时,最大程度地减少光谱失真。
1 IHS模型改进
1.1 IHS模型
传统的基于IHS变换的图像融合方法因其简单高效的特点被广泛应用到遥感软件中[9],其步骤为[10]:首先,对全色影像和多光谱图像进行几何校正,并对多光谱影像重采样,使其宽高与全色影像一致;其次,选择多光谱图像的红、绿、蓝波段进行IHS正变换,得到I0、H、S3个分量;再次,采用融合规则将全色图像与I0融合,得到新的亮度分量Inew;最后,用Inew替换I0,再进行IHS逆变换得到融合后的图像。
全色图像和I0的融合规则常采用直接替换法和直方图匹配法。直接替换法就是将全色图像作为Inew;直方图匹配法就是将全色图像和I0的直方图匹配结果作为Inew。
1.2 改进的IHS模型设置
传统的基于IHS变换的融合图像存在一定的光谱失真,RAHMANI等[11]提出了AIHS(adaptive intensity-hue-saturation,自适应IHS)方法对IHS变换进行改进,主要包括以下改进策略:
1)提高空间策略
根据IHS变换,可以在多光谱和亮度分量I之间建立线性关系:
I=∑nαnMn
(1)
其中:M为待融合的多光谱图像,n为多光谱波段数。同时,认为全色影像PAN能近似替代I,并结合公式(1)可建立线性关系:
P≈∑nαnMn
(2)
其中,P为全色图像。为了求解α,建立了如下函数:
minG(α)=∑i,j(∑nαnMn(i,j)-P(i,j))2+λ∑n(max(0,-αn))2
(3)
式(3)等号右边第二项为α的非负约束。在融合之前,对全色图像进行直方图匹配,保证全色图像和多光谱图像的均值和标准差在同一范围内。
(4)
2)提高光谱策略
在IHS变换中,融合后的图像会丢失边缘和纹理信息。为避免这个问题,可以从全色影像中提取边缘和纹理信息,再和多光谱影像进行IHS融合。
Fn(x,y)=Mn(x,y)+h(x,y)(Pnew(x,y)-I(x,y))
(5)
(6)
其中:F(x,y)表示融合后图像,h(x,y)为边缘检测函数,λ=10-9,ε=10-10,▽Pnew(x,y)是经过直方图匹配后的全色图像在(x,y)处的梯度。
1.3 边缘信息保持
为了保持边缘信息,LEUNG等[12]提出利用全色图像和多光谱图像各通道的边缘检测矩阵的加权和作为融合图像的检测矩阵,再按各个通道间的比例提取信息。其公式如下:
(7)
其中:βi由公式(8)求解;WMi和WPnew分别表示多光谱和全色图像的边缘检测矩阵。可由公式(6)计算。
(8)
本文中采用多光谱图像的亮度分量的边缘检测矩阵WI替换WM,则β和h(x,y)由下式求解:
(9)
(10)
(11)
最后,可得到融合后图像F:
Fi=Mi+hi×(Pnew-I)
(12)
1.4 本文的模型设置
融合图像是由全色图像和多光谱图像互补合成,其空间信息来自全色图像,光谱信息来自多光谱图像,据此可以提出两种假设:1)全色图像是融合图像各波段的线性组合;2)多光谱图像是融合图像经过低通滤波再下采样后的图像[8]。基于这两个假设提出了一种优化目标,通过对目标进行优化,得到最优控制参数,利用具有最优控制参数的自适应模型重构出融合图像。两个假设的数学表达如下:
(13)
Mn(x,y)≈∑i,jK(i,j)Fn(x-i,y-j)
(14)
其中,K是3×3的低通滤波模型。结合两个假设和公式(8),建立的目标函数如下:
minH(α,θ,β,K)
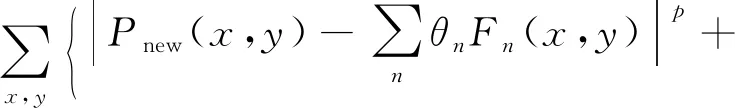
‖WPnew-βWI‖2
}
s.t.β≥0
0≤αn≤1,n=1,2,…,N
0≤θn≤1,n=1,2,…,N
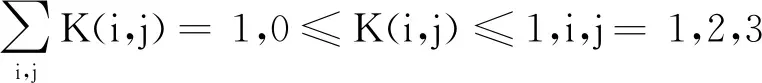
(15)
2 改进的松鼠搜索算法
2.1 松鼠搜索算法
JAIN等[13]于2018年提出的一种模仿松鼠动态觅食行为和有效运动方式的群体智能优化算法,即松鼠搜索算法(squirrel search algorithm,SSA)。松鼠是一类栖息在树上的啮齿目动物,其主要靠滑行进行移动。松鼠滑翔被认为是最复杂的空气动力形式,也是最节能的[14]。它的动态觅食行为也使食物资源得到最有效的利用[15]。在SSA中,有4个必要的假设:
1)在森林中,有n只松鼠和n棵树,1棵树上有1只松鼠。
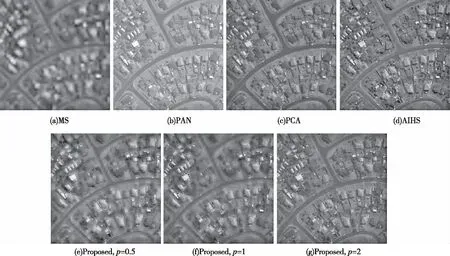
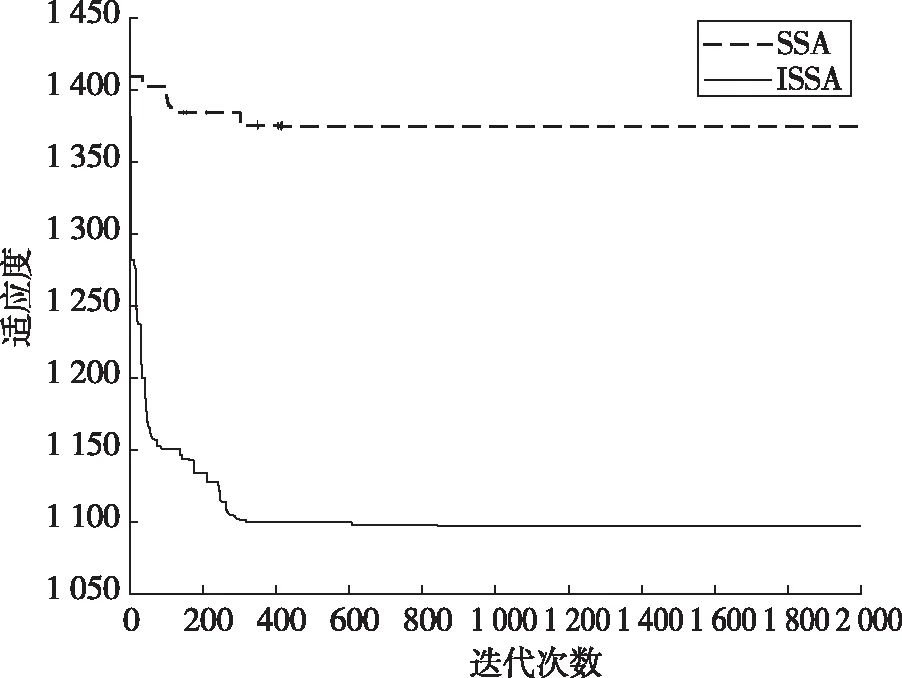
2)这n棵树包括1棵山核桃树和NS(1 3)森林里只有3种树木。山核桃树有最好的食物(山核桃),橡子树有较一般的食物来源(橡子),而普通的树没有食物。 4)每只松鼠都单独寻找食物,并通过动态的觅食行为来寻找可利用的食物资源。 2.1.1种群初始化 在算法中每个松鼠依据下面的公式进行初始化: Si=SL+rand(1,d)×(SU-SL) (16) 其中:Si表示第i个个体的适应度值,SL和SU分别表示搜索空间的下界和上界,rand(1,d)表示大小为1×d的范围为0到1的随机数矩阵,d为解的维度。 2.1.2对个体进行分类 每个松鼠位置的优劣由适应度值评价。每个松鼠的位置被输入适应度函数f,计算每个松鼠当前的适应度值:f(Si)=f(Si,1,Si,2,…,Si,d),i=1,2,…,n,适应度值越小代表食物质量越高。之后,对种群个体依据适应度值从小到大排序,将排序第1位的个体代表山核桃树上的松鼠(Sh),排序第2到NS+1位的个体代表位于橡子树上的松鼠(Sa),其余的代表位于普通树上的松鼠(Sn)。 2.1.3更新个体位置 在SSA算法中,个体更新位置的方式是模拟松鼠滑行运动。位于普通树上的松鼠可能有一部分会朝山核桃树移动,另一部分朝橡子树移动;位于橡子树的松鼠会朝着山核桃树移动。在这些情况下,可以得到松鼠更新个体位置的公式: (17) (18) (19) 其中:t为迭代次数,R为0到1之间的随机数,Pdp为捕食者存在的概率。如果R≥Pdp,松鼠不会被捕食;否则松鼠处于危险中,必须要在周围寻找藏匿地点。Gc是松鼠滑行常量,在原文中Gc=1.9。dg代表滑行距离,计算公式为 (20) 其中,φ表示滑行角度,计算公式如下: (21) D是牵引力,L为升力,可按下式计算: (22) (23) 其中:ρ为空气密度,ρ=1.204 kg/m3;v=5.25 m/s,表示松鼠滑行速度;s=154 cm2,表示松鼠身体表面积;cD、cL表示牵引力和升力的摩擦阻力系数,cD=0.6,cL∈(0.675,1.5)。 2.1.4季节变换 在SSA算法中,模拟季节变化对种群内个体进行检测,有助于算法跳出局部最优。在每次迭代开始时,算法要求种群处于冬季状态,这意味着每个个体按照2.1.3节更新后,季节开始转换,季节的变化由下面两个公式决定。 j=1,2,…,Nfs (24) (25) (26) (27) ra、rb为[0,1]之间的随机数,β=0.5,σ可以用下面的公式计算: (28) 在本节中,引入自适应步长策略[16]、适应性捕食者概率[17]、高斯算子和柯西算子来改善SSA。采用自适应步长策略和适应性捕食者概率来更新位置,平衡个体的探索能力。在此基础上,引入高斯算子和柯西算子,增加种群的多样性。 2.2.1自适应步长策略 在原算法中,需要对Gc不断调整来得到相应的探索能力。Gc越大,探索能力越强,却不利于解决各种复杂的优化问题。因此,引入了一种自适应步长策略,能较有效地解决这个问题。 rha=2logsig(ωha)-1 (29) rhn=2logsig(ωhn)-1 (30) ran=2logsig(ωan)-1 (31) 其中,ω为个体间的欧式距离,可由下式计算: (32) (33) (34) 在这里,d是优化问题解的维度。 2.2.2适应性捕食者存在概率 在算法迭代刚开始时,种群内松鼠分布较为分散,不能有效防止捕食者的捕食。随着迭代进入后期,种群内松鼠离最优位置越来越近,分布也越来越集中,更能减小被捕食的概率[18-20]。因此,引入适应性捕食者存在概率,其计算公式如下: (35) 其中,Pdp,max、Pdp,min分别表示捕食者出现的最大、最小概率。 2.2.3两种算子 当捕食者出现时,待在原位置的松鼠有被捕捉的危险,需要立即找寻最近的藏身地点。在本文中,引入高斯算子和柯西算子来产生新位置。通过分析,柯西算子步长较大,探索能力较强,对于具有较小适应度值的位于橡树上的个体采用柯西算子更新位置,能引导种群跳出局部最优;高斯算子步长较小,探索能力相对较弱,位于普通树上的个体采用高斯算子更新位置。结合自适应步长策略可得个体更新位置的公式: (36) (37) (38) 其中:G和C分别表示服从高斯和柯西分布的随机数,两种分布的概率密度函数如图1所示;T为最大迭代次数,t为当前迭代次数,y=logsig(x)的图像如图2。改进的松鼠搜索算法伪代码如表1所示。 图1 高斯和柯西分布的概率密度函数 图2 logsig函数 表1 改进的松鼠搜索算法伪代码 主观评价法是一种简单、快速的评价方法,评价人能快速地对融合质量的优劣进行判断。本文中选择从颜色特征和轮廓特征两个方面对融合质量进行评价。然而,主观评价方法具有一定的片面性,所以再选择常用的无参考图的融合质量评价指标QNR[21]对融合效果进行评价,其公式为 QNR=(1-Dλ)×(1-Ds) (39) (40) (41) 其中:QNR为联合光谱和空间质量指数;Ds为空间扭曲指数;Dλ为光谱扭曲指数;M、P和F分别表示多光谱图像、全色图像和融合后图像;PL表示低空间分辨率的全色图像;Q(·)表示计算UIQI[22]的函数,公式为 (42) Ds和Dλ越小,QNR越大,融合质量越好。Ds和Dλ最优值为0,QNR最优值为1。 3.2.1主观对比分析 对结果进行直观的比较,MS图像、PAN图像以及融合后的图像分别如图3和图4所示。这些方法都可以有效地融合PAN和MS图像,但融合效果存在差异。可以看出,本文方法比其他算法获得了更好的空间信息,PCA和AIHS方法存在光谱失真。在图3和图4中:(c)光谱信息丰富,但光谱分辨率较低;(d)空间信息保持较好,但存在光谱失真;(e)边缘信息丢失严重,图像较模糊;(f)比(e)更清晰,空间分辨率有所提高,但仍然存在模糊现象;(g)空间信息和光谱信息保持较好,视觉相对平滑。 图3 QuickBird卫星源图像及融合结果 图4 IKONOS卫星源图像及融合结果 3.2.2客观对比分析 各种方法的QNR值如表2和表3所示。首先,从空间扭曲指数Ds和光谱扭曲指数Dλ两项来看,本文中所采用方法的空间畸变和光谱畸变值都较小,表明空间细节和光谱保持较好。AIHS方法性能不佳,它的一个主要缺点是光谱失真。以将边缘从PAN图像转移到融合图像为目标,AIHS方法中的加权矩阵,是PAN图像边缘的函数。由于在PAN图像中出现的边缘可能不会出现在每个MS波段中[12],因此不适合在不同波段中注入相同数量的细节。本文中采用的模型由于考虑了融合后图像与原始多光谱图像的光谱一致性,以及波段间比例一致性,从而减小了融合后图像的光谱失真,融合效果较好。然后,整体考虑空间和光谱畸变,从QNR指标来看,对于两组图像,文中所采用的方法QNR值最大,表明空间信息和光谱信息保持最好,融合效果最好。最后,观察原始的松鼠搜索算法和改进的松鼠搜索算法的收敛性,从图5可以发现,改进的松鼠搜索算法由于引进了自适应策略和两种算子,相对原始算法,收敛速度有所提高。 表2 图3和图4客观评价指标 表3 25组图像均值 图5 SSA和ISSA最优个体适应度变化 通过实验对比分析可知,本文中采用的图像融合方法融合效果显著,同时改进的松鼠搜索算法相对于原始的松鼠搜索算法具有较强的收敛性和寻优能力。但是,单目标优化相对于多目标优化存在一定缺陷,在以后的研究中,将考虑建立多目标优化模型,同时将SSA算法与Pareto支配原理结合[23-25]用于控制参数的优化。
2.2 改进方法


3 实验对比与分析

3.1 融合质量评价方法
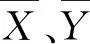
3.2 主观及客观分析



4 结语
