基于普通匿名区域生成的改进算法
2022-03-31王智明
王智明
(莆田学院 机电与信息工程学院,福建 莆田 351100)
基于位置的服务(location based services,LBS)集成了测绘、卫星导航、GIS等技术,为我们提供诸如地图导航、网约车、广告推送等各式各样便利的服务。然而作为硬币的另一面,这些海量数据中不可避免会包含一些企业或个人的隐私数据[1]。早在2002年,SWEENEY提出k-匿名(k-anonymity)模型[2],2006年,MACHANAVAJJHALA[3]对该模型进行改进,提出了L-diversity,规定每个信息属性等价类不能少于L个敏感属性值。2016年,LI等[4]通过删除最远足迹的方式提高了LBS服务质量。PALANISAMY等[5]要求用户离开Mixzone区时使用假名,以通过区域关联性的攻击。
匿名区域切换过程中常见的三种攻击:(1)中心点攻击,计算切换前后匿名区域的中心点,如果重合,则攻击者认为是来自同一用户的请求,不重合则放弃攻击;(2)等比缩放攻击,攻击者在服务器上获取切换后的匿名区域,保持中心点不变按前后隐私度k比例进行等比缩放,计算切换前的匿名区域。(3)线性偏移攻击,攻击者在服务器上对用户发来的匿名区域中心点进行记录,通过一段时间的观察,推测出匿名区域切换前后的线性关系,破解线性偏移函数。
普通匿名区域生成算法依据匿名区域切换前后的隐私度k的比值,保持中心点不变等比缩放原匿名区域,这样很容易被中心点攻击者攻破,而切换前后的匿名区域存在较大的交集,不能很好对付对等比缩放攻击。线性偏移攻击虽然前期无法对普通匿名区域生成算法构成威胁,但随着用户申请次数的增加,线性偏移方程被破解的可能性加大。综上,普通匿名区域生成算法不能很好应对三种类型攻击。
1 基于普通匿名区域生成的两种改进算法
1.1 迭代搜索线性偏移区域切换算法(算法1)
普通匿名区域生成算法在切换匿名区域时,保持区域中心点不变或简单进行线性偏移,容易为恶意者所攻击,不能有效抵御中心点攻击和线性偏移攻击,本节对普通匿名区域生成算法进行改进,提出迭代搜索线性偏移区域切换算法(算法1),具体步骤如下:
(1)将原匿名矩形区域中心点O作为坐标原点,将矩形区域分为I、II、III、IV面积相等的4个子矩形区域,从左上子矩形顺时针方向依次记为R1、R2、R3、R4,计算各子矩形的用户数Ni=c(Ri),选取Ni值最大的区域Ri作为迭代矩形,进一步划分为四个子矩形,直到MAXNi≤3,划分结束。
(2)从Ri区域随机选一用户U,连接O、U两点的直线y=ax+b作为偏移函数。如图1(a)所示,迭代搜索的矩形编号依此为2、7、10,则从10号矩形中随机选用户。
(3)依据切换前后的隐私度k的比值,中心点不变等比例缩放原匿名区域,生成初步匿名区域CK1。区域4个顶点依次记为(xLeft,yTop)、(xLeft,yBot)、(xRight,yTop)、(xRight,yBot)。
(4)根据用户确定的横坐标位移量△x,由偏移方程y=ax+b可得△y=a△x,令xLeft=xLeft+△x、xRight=xRight+△x、yTop=yTop+a△x、yBot=yBot+a△x。
(5)将(xLeft,yTop)、(xLeft,yBot)、(xRight,yTop)、(xRight,yBot)作为四个顶点分别映射到x、y坐标轴,生成线性偏移切换后的区域CK2,如图1(b)所示。
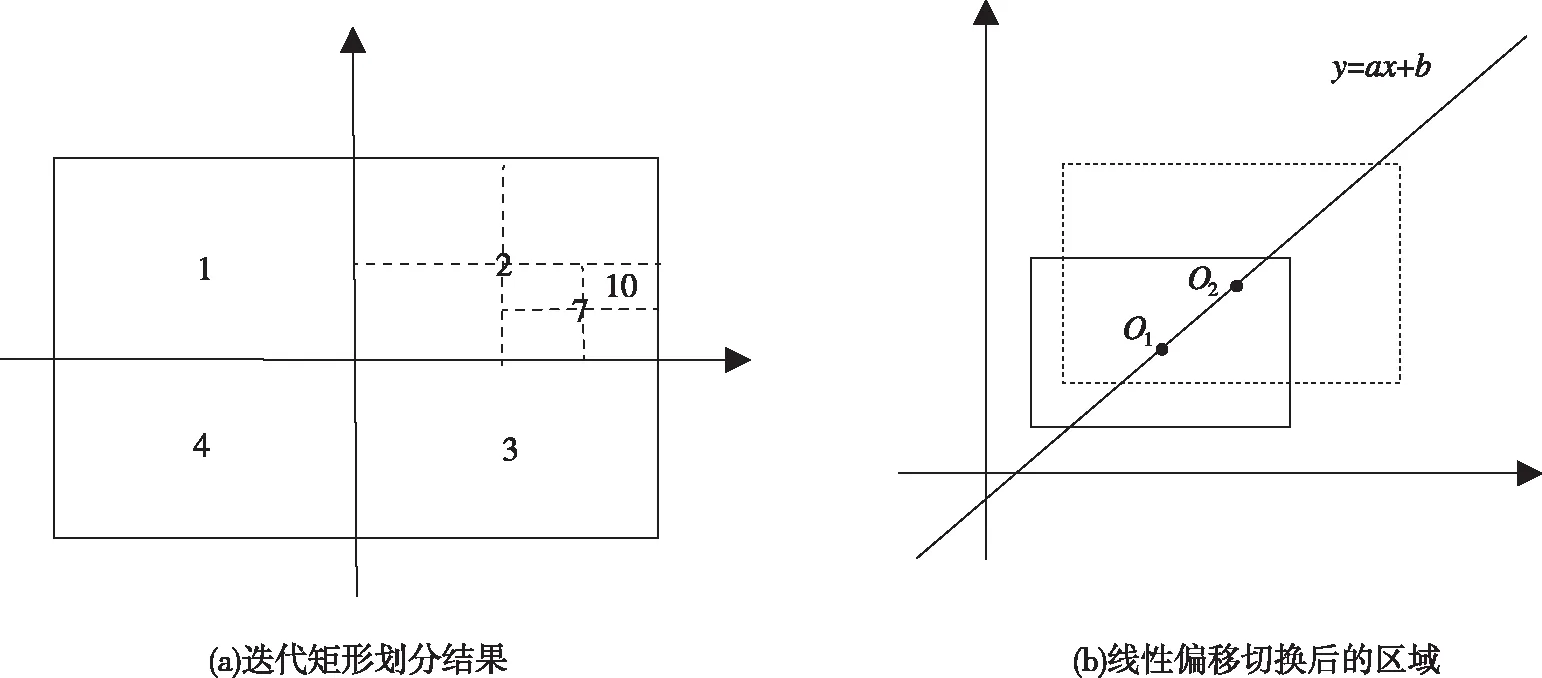
图1 迭代搜索线性偏移区域切换算法
(6)为匿名区域CK2构建用户集合U2,并计算集合用户数N=C(U2)。
(7)若N≥k,且CK2的面积SCK2≤Smax,则匿名区域切换成功,跳到步骤(10)。其中k表示切换后隐私度,Smax表示用户可接受的最大隐私区域面积。
(8)若N (9)若SCK2>Smax,则保持区域中心点不变等比缩小匿名区域CK2至Smax,即SCK2=Smax,返回步骤(6)重新计算用户数量。 (10) 返回线性偏移后的匿名区域CK2,算法结束。 迭代搜索线性偏移区域切换算法针对普通匿名区域生成算法的中心点不变进行优化,对等比缩放后的匿名区域进行线性偏移,偏移方向依据用户密度具有随机性,其区域偏移的规律难被攻击者捕获,能很好应对中心点和线性偏移的攻击,系统综合开销也比较小,但该算法不足是存在被等比缩放攻击的风险。 迭代搜索线性偏移区域切换(算法1)基于用户密度进行线性偏移,具有一定动态性和随机性,能较好抵抗攻击,但当切换区域前后偏移位移较小时,仍然存在被等比缩放攻击的风险。本节通过对算法1改进,提出分布式匿名区域外溢切换算法(算法2),具体步骤如下: (1)对原匿名矩形区域CK的4个顶点做两对角线,从上矩形边顺时针方向将区域分为I、II、III、IV四个三角形子区域,依次记为T1、T2、T3、T4,四条矩形边依次相应记作L1、L2、L3、L4。计算T1、T2、T3、T4各区域内的用户数Ni=c(Ti),选取用户密度值ρ=Ni/STi(STi表示Ti区域面积)最大的两个区域,生成这两区域对应i值的集合{m,n}。分别令i=m、n,重复执行(2)至(12)步骤两次,最终得到两个分散的匿名区CKm、CKn。如图2(a)所示。 (3)以Li的中点O作为圆心,r为半径画圆,如图2(b)所示,以边Li(包括延长线)为中线,选取位于匿名区域外侧的半圆区域CKr。 图2 分布式匿名区域外溢切换算法 (4)初始化空用户集U={∅} ,生成半圆区域CKr的用户集U。 (5)将U内所有用户点映射到x、y坐标轴,得到区域边界用户点相应的x、y轴极值xmin、xmax,ymin、ymax。 (6)以(xmin,ymin)、(xmin,ymax)、(xmax,ymax)、(xmax,ymin)为4个顶点,生成切换后的匿名区域CKi,计算集合用户数N=c(U)和CKi区域的面积SCKi。 (12)匿名区域切换完成,返回匿名区域CKi,算法结束。 分布式匿名区域外溢切换算法利用了用户的分布密度,同时对原匿名区域做了外溢处理,攻击者很难获取用户真实地址,区域切换的成功概率高。切换后的匿名区域是由两块区域(CK1、CK3)组成如图2(a),这样能有效提高用户的服务满意度[6],因为在单匿名区域情况下,如果用户需要的服务点刚好落在新匿名区域中或者靠近原匿名区附近,用户可以达到较高的满意度;但是如果用户需要的服务点落在新匿名区远离原匿名区那一侧,而用户真实位置刚好又位于原匿名区中远离新匿名区的那一侧,则服务质量差,用户满意度低。 综上,分布式匿名区域外溢切换算法能很好应对中心点、线性偏移、等比缩放三类攻击,安全性和用户服务满意度显著提升,但算法开销相对较大。 普通匿名区域生成算法存在问题:当用户请求区域切换次数越大时,中心点线性偏移函数被攻破的压力就越大;算法2安全性、用户服务满意度高,但算法较复杂,时间开销较大。算法1的系统开销与安全性介于上述两算法之间。因此在LBS的实际应用中,可在用户请求切换的次数N值较小时,使用普通匿名区域生成算法,当N值较大时,依据安全性和用户服务质量需求选择算法1或算法2,充分做到扬长避短,具体步骤如下。 PROCEDURE: Ni=c(USERi); IFNi≤5 THEN DO 普通匿名区域生成算法; IFNi>5 AND RISK(等比缩放攻击)=0 THEN DO本文算法1; ELSE DO 本文算法2; END PROCEDURE 试验环境为处理器Intel(R) Core(TM)i3-4170@3.70 GHz CPU,8 GB内存,1 TB硬盘,Python 2.7.12。 匿名区域切换的耗时会直接影响到用户的体验,是衡量算法的重要指标之一。3种匿名区域切换算法的耗时试验结果见表1。可以看出:普通匿名区域生成算法耗时明显小于另外两算法,这是由于普通匿名区域生成算法仅依据切换前后隐私度k值等比例扩大原匿名区域,算法简单,生成新匿名区域的速度比较快。当切换前隐私度k=1时,切换后隐私度k值越大其所对应的耗时随之呈增加的趋势,但并不是呈成正比例增加。耗时与切换前后△k值变化有关,当△k较小时切换耗时较少,△k值较大时迭代搜索线性偏移区域切换算法和分布式匿名区域外溢切换算法的耗时增加较多,但其总耗时能够控制在用户可接受的范围之内[7]。在时间消耗方面,普通匿名区域生成算法耗时最少优势明显,然后依次是迭代搜索线性偏移区域切换算法、分布式匿名区域外溢切换算法[8]。 表1 不同算法的匿名区域切换耗时 由以上结果可知,在注重时间效率而对安全性不敏感的场景下可以优先采用普通匿名区域生成算法进行匿名区域的切换。 匿名区域切换成功率是生成新匿名区域的成功概率,它间接影响了用户位置的泄露概率,是区域切换算法安全性的重要指标之一。在中心点与等比缩放两种不同攻击情况下,3种算法区域切换的成功率分别见表2和表3。可以看出,在两种攻击情况下,普通匿名区域生成算法的切换成功率均维持在[0.00%,0.05%]之间的低水平。这主要归因于普通匿名区域生成算法切换前后中心点保持不变,容易遭受中心点和等比缩放攻击而导致用户真实位置泄露[9-10]。 表2 中心点攻击下不同算法的匿名区域切换成功率 表3 等比缩放攻击下不同算法的区域切换成功率 由表2得知,迭代搜索线性偏移区域切换算法在中心点攻击时,能够保持很高的切换成功率,大多数情况非常接近100%,这是由于该算法针对中心点攻击的特点,对匿名区域的中心点进行了线性偏移[11]。而表3数据显示,在面对等比缩放攻击时,该算法的表现就不尽人意,最高的成功率只有34.96%,有的情况只是个位数,究其因主要是切换前后的隐私区域存在一定的重叠面积,若用户真实位置刚好处于其中,则会导致位置泄露[12-13]。 由表2、表3看出,分布式匿名区域外溢切换算法在面对中心点攻击和等比缩放攻击时,都有良好表现,切换成功率达到了100%。这是由于该算法在区域生成时,按用户密度来决定切换后区域的方位,同时对原匿名区域做了外溢处理来减少用户真实位置泄露的风险,所以有效抵御了各类攻击[14-15]。 随着LBS服务应用的纵深发展,个人位置隐私泄露的风险越来越大。通过对个人位置隐私保护技术的分析和研究,改进了普通匿名区域生成算法,提出的迭代搜索线性偏移区域切换算法保留了时间开销小、响应速度快的优点,能有效抵御中心点和线性偏移攻击;分布式匿名区域外溢切换算法进一步引入了用户密度与分布式概念,能进一步有效抵御等比缩放攻击。在不同的应用场景,依据用户申请切换的次数,将两种算法结合起来使用能达到更好效果。1.2 分布式匿名区域外溢切换算法(算法2)


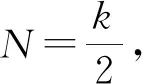

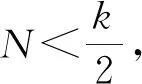

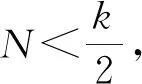
1.3 算法1和算法2的综合应用
2 试验和结果分析
2.1 3种匿名区域切换算法的耗时比较

2.2 3种匿名区域切换算法匿名区域切换成功率


3 结语
