深空网干涉测量数据对嫦娥五号定轨能力分析

孔 静，张 宇，任天鹏，欧阳琦，李翠兰，段建锋，慎千慧，陈 明

(1. 北京航天飞行控制中心，北京 100094；2. 航天飞行动力学技术重点实验室，北京 100094)

0 引 言

航天器精密轨道确定是空间探测活动的一项关键性技术，关系着探测任务的成败，科学数据的应用成效。在深空探测方面，测控系统经过了十多年的努力，跟踪测量能力得到了大幅提升。在嫦娥一号任务中，测控系统采用了统一S频段(Unified S-band, USB)与中国VLBI网(Chinese VLBI network, CVN)的甚长基线干涉测量技术(Very long base interferometry, VLBI)跟踪测量模式完成探测器的测轨工作。嫦娥一号任务实施期间，中国深空网(China’s deep space network,CDSN)尚未建成，为了月球探测任务的顺利实施，测控系统对USB设备进行改造，采用三程开环测量模式，由位于青岛与喀什的12 m天线发射上行信号，18 m天线接收下行信号，获取三程测距与测速数据。CVN由位于上海、北京、昆明与乌鲁木齐的4个VLBI站及位于上海的数据处理中心组成。嫦娥二号任务中，上海天文台采用数字基带转换器取代传统的模拟基带转换器，改善带通非线性效应，将VLBI测量的时延精度提升至3 ns。嫦娥三号任务VLBI测量技术得到进一步提升，并实现了利用X频段双差单向测距的多信号处理能力。嫦娥四号任务实现VLBI系统分时快速转换跟踪处理技术，确保了多目标的实时跟踪处理，有力保障了任务的实施。CDSN于2012年建成投入使用，目前包括佳木斯(66 m)、喀什(35 m)、位于南美的阿根廷站(35 m)，以及位于纳米比亚的深空天线。深空网近乎全球的分布，极大地提升了深空探测器的跟踪覆盖能力。深空站虽然主要用于USB/UXB跟踪测量，北京航天飞行控制中心也尝试利用深空网开展VLBI跟踪试验，相关跟踪测量得到了实战应用验证，多次试验任务获取了优于3 ns的时延观测值。CE-5采样返回试验中，深空网干涉测量系统(Deep space VLBI Network,DVN)利用深空网有效获取了干涉测量数据。

月球探测任务采用USB/UXB+VLBI测量模式，主要是考虑VLBI测量对于视线垂直方向上的轨道变化敏感，可以弥补传统测距、测速技术只对轨道提供视向约束的不足。历史数据的处理分析显示，VLBI测量对于地月转移轨道解算的贡献较环月飞行段更为显著。在地月转移阶段，VLBI测量的系统差会对轨道解算精度产生显著影响，而由于观测几何相对较差，该系统差一般难以在定轨计算中进行解算。因而，VLBI测量的系统误差标校与消除对于测控系统尤为重要。CVN采用射电源-航天器-射电源(Q-S-Q)跟踪模式，通过跟踪射电源标校基线间的设备时延，极大程度的消除设备延迟影响，对于对流层传播介质延迟则采用水汽辐射计进行修正。

CE-5由轨道器、上升器、着陆器和返回器4部分组成，其中轨道器和上升器携带有VLBI信标机，满足VLBI跟踪测量要求。本文对DVN发布的VLBI跟踪数据进行处理，分析DVN时延的引入对不同飞行阶段轨道精度的提升，为后续深空网跟踪测量数据对探月任务的支持提供依据。

1 深空网干涉测量系统

1.1 测量原理

VLBI测量的基本原理是航天器发射下行信号后，地面2个测站接收航天器下行的同一波前信号，并对同源信号进行相关处理，结合航天器先验的位置信息提取同源信号到达两测站的时延差。时延测量本质是差分单向测距，根据VLBI测量机理可知，时延观测值不仅仅取决于航天器与测站的几何位置关系，还与航天器下行信号穿过的空间环境、设备链路时延的修正精度密切相关。

DVN利用中国深空网跟踪接收航天器下行信号，进行相关处理获取时延观测。深空站的主要职责仍然是负责航天器的测轨、数传与遥控工作，因而深空站在航天器测控弧段内必须全时段指向航天器，以确保测控及遥测工作的顺利完成，短时间内的Q-S-Q交替观测模式不适用。为了最大限度的利用射电源标校设备链路延迟，DVN采用稀疏交替射电源标校技术完成射电源的标校，部分实现了设备链路延迟的标校。

1.2 测量误差分析

VLBI测量获取的是航天器下行信号到达2个地面站的时间差，包括信号传播路径中的对流层、电离层延迟，地面站设备之间信号传输延迟，以及基线间的时间同步差异。

深空网都配备了水汽辐射计、GNSS双频接收机以及气象仪等大气参数测量设备，以完成目标视向传播介质时延误差的近实时修正，设备测量对传播介质产生的延迟修正精度为厘米级。

站间时间同步误差主要采用GPS共视法处理，通过接收GPS时间信号测量位于两地测站时钟的时差，实现高精度站间时间同步,多站联合的站间时间同步精度优于20 ns。再通对本地时钟与GPS标准时钟的长期比对，可以构造钟差随时间变化的模型，通过多项式构建钟差模型进一步提升测站间时间同步精度。

设备链路延迟的标校需要结合射电源标校技术，深空网干涉测量系统采用稀疏交替射电源标校技术标校设备延迟和残余的钟差，但由于深空网在跟踪弧段内必须全时段指向航天器，射电源标校的时间间隔可达数小时至十几个小时，存在残余的标校误差，而且由于链路误差与空间环境密切相关，呈非线性变化，射电源标校后的残余系统偏差也呈现非周期性抖动，难以通过数学建模进行进一步消除，这是DVN试验观测的主要误差源。

2 DVN时延数据质量分析

嫦娥五号任务中，DVN主要使用了2条基线接收VLBI信标机下行信号：基线1(佳木斯——喀什)，基线2(纳米比亚——阿根廷)。其中，基线1在国内测控区，与CVN测轨分系统的跟踪弧段基本重合，基线2的测控弧段则可以有效补充国内测控区无法覆盖的跟踪弧段。

整个任务阶段，DVN共进行了约20组跟踪，本节选取CVN跟踪覆盖较好的弧段，利用地基UXB与CVN数据解算精密轨道，标校深空干涉测量系统VLBI的数据误差。图1所示为选取的跟踪弧段，共计15组数据，其中前4组为转移阶段，后11组为环月飞行阶段。

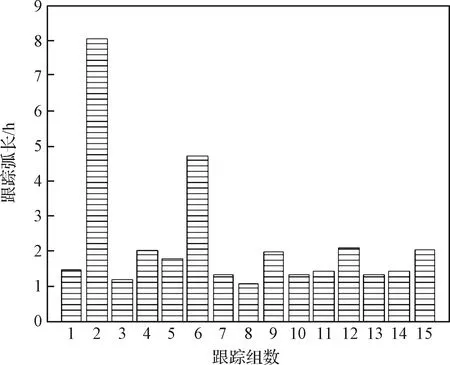
图1 跟踪弧长统计Fig.1 Arc length statistice

表1为精密轨道计算使用的基本策略。基于该策略对所选取弧段的地基UXB与CVN数据进行处理。解算轨道结果通过重叠弧段轨道比较，可以实现地月转移段优于百米的轨道解算精度，近月制动前期可优于50 m，环月阶段轨道精度可优于50 m。

表1 精密轨道解算策略Table 1 Orbit Determination Strategy

图2～图5给出了几组典型的试验数据的残差情况，转移阶段与环月飞行阶段各给出了2组，残差结果相对之前探月数据的处理稍差。由于频繁的姿控调整、卸载喷气、点频切换等因素的影响，测量数据的残差呈非白噪声，增加了轨道解算的难度，一定程度上降低了轨道精度。

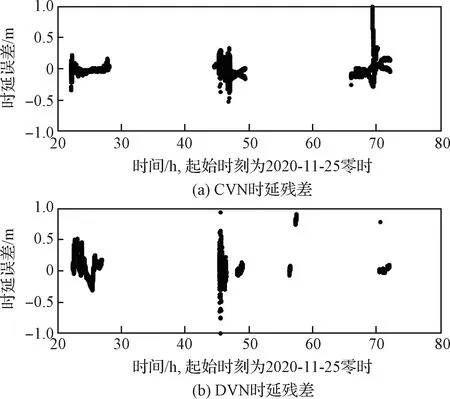
图2 11月25日VLBI数据定轨残差Fig.2 Post fit VLBI Residuals on 2020- 11- 25

对所有弧段的DVN时延数据残差进行统计，考虑到DVN数据存在一定的系统偏差，首先进行系统偏差的标校。利用解算的精密轨道计算DVN观测弧段对应的理论值，再计算观测值与理论值的偏差，并剔除残差绝对值大于3倍方差的观测数据，最后统计残差的均值作为DVN数据的系统偏差。进行系统偏差标校后的DVN试验数据RMS(Root mean square)大约为0.45 m。图6给出了每个DVN跟踪弧段统计的系统偏差，最大偏差近1.4 m。

图3 12月13日VLBI数据定轨残差Fig.3 Post fit VLBI Residuals on 2020- 12- 13

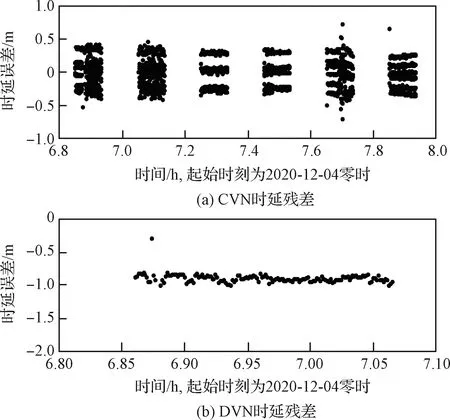
图4 12月04日VLBI数据定轨残差Fig.4 Post fit VLBI Residuals on 2020- 12- 04

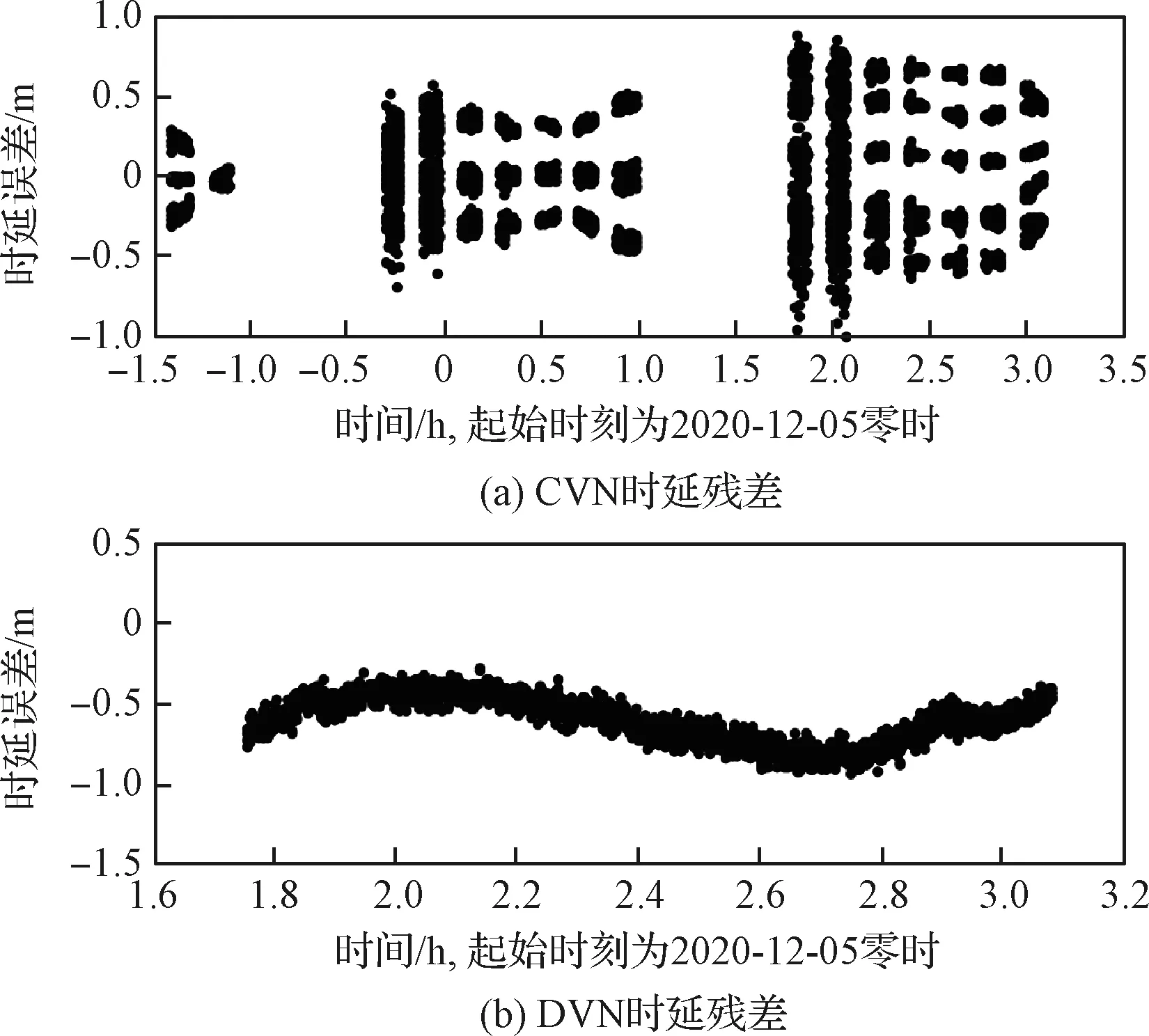
图5 12月05日VLBI数据定轨残差Fig.5 Post fit VLBI Residuals on 2020- 12- 05

图6 DVN时延标校误差Fig.6 Delay calibration error of DVN

3 基于深空网数据的轨道解算

针对上述选取的弧段分别采用不同策略进行定轨计算，以分析DVN数据对轨道解算的贡献，CVN分系统的测量数据用于基准轨道的建立。深空网所提供的数据包括测距、测速数据以及DVN提供的时延数据，本节选取3种数据组合与使用方式：1)深空网测距、测速数据；2)深空网测距、测速数据+DVN数据；3)深空网测距、测速数据+系统差标校后的DVN数据。利用基准轨道评估解算轨道的精度，定轨策略同表1。

3.1 利用测距与速度的轨道解算

单独利用深空网测距、测速数据进行定轨计算，定轨策略同表1。将定轨计算的结果与基准星历进行比较，并统计星历偏差(图7～图8)。转移飞行阶段，轨道偏差均超过1 km，对于环月飞行阶段轨道小于200 m(超过100 m的算例有3组)。转移阶段，相对融合UXB与VLBI解算的百米级轨道，仅利用UXB数据的定轨精度大幅降低，该结果与早期探月任务的分析相一致，虽然深空站测量精度的提升可以在一定程度上改善定轨精度，对于地月转移阶段，仍然只能实现千米级的轨道精度，精确稳定轨道的解算仍然依赖VLBI测量数据的融合处理。

图7 转移段轨道解算偏差统计Fig.7 Statistics of orbit deviation for transfer segment

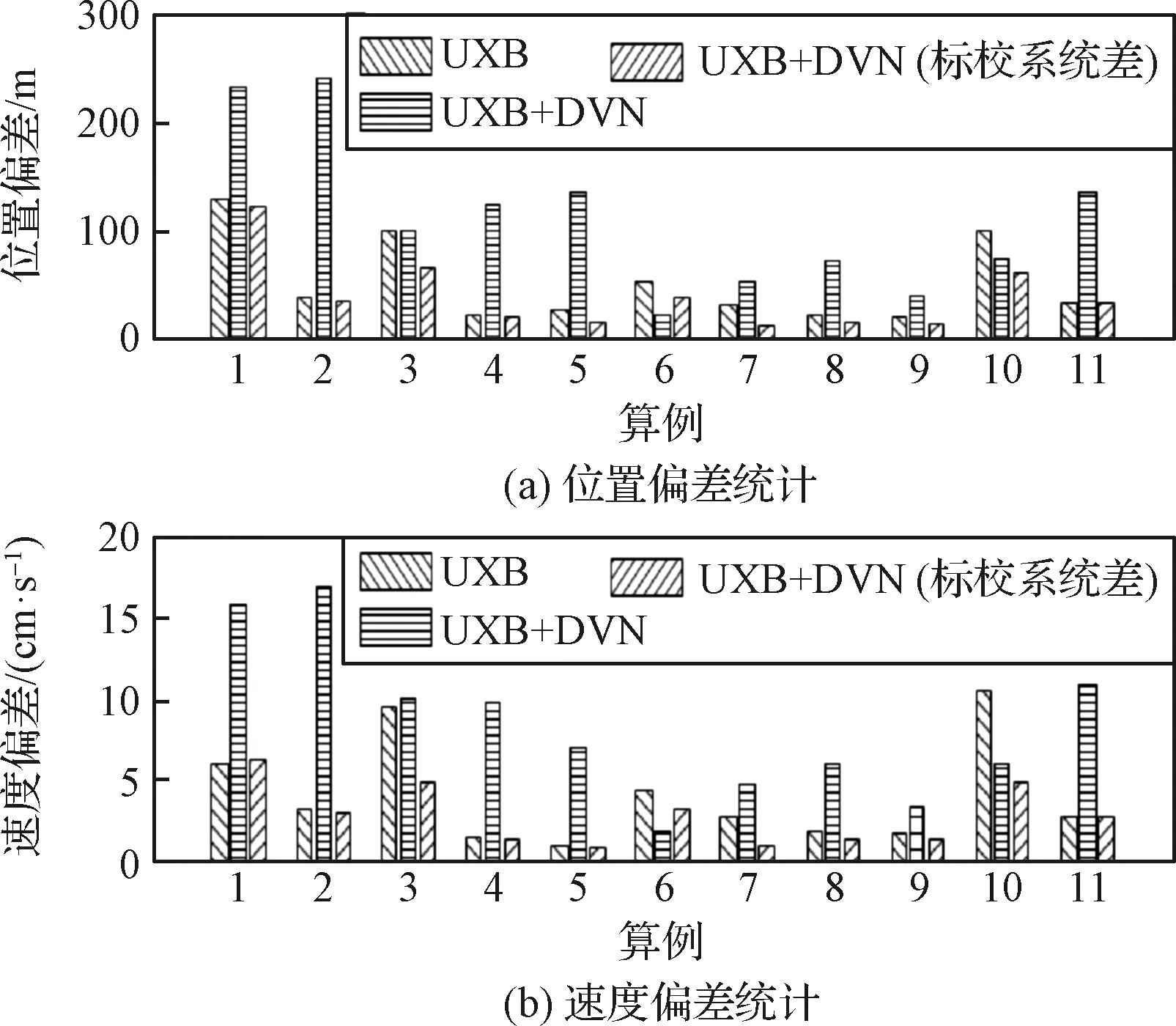
图8 环月段轨道解算偏差统计Fig.8 Statistics of orbit deviation for orbiting phase

3.2 深空网测距、测速及时延数据的轨道解算

引入DVN数据参与定轨，以改善观测几何，提升轨道精度。考虑到部分DVN的时延数据存在一定的系统偏差，分析考虑2种策略：1)定轨计算不解算时延系统差，解算轨道包含系统误差的影响；2)利用基准轨道标校时延数据的系统偏差，再进行轨道改进。

统计两种策略解算的轨道与基准轨道的偏差(图7-8)。转移阶段的4组算例轨道精度均能优于1 km，标校系统偏差后轨道偏差均小于500 m,相对单独UXB数据定轨精度有近1倍的提升；环月阶段，DVN数据的引入并没有显著改善轨道精度，部分算例轨道精度反而下降，标校DVN数据系统差后，定轨精度有一定改善，但仍与UXB定轨精度相当。

3.3 基于协方差理论的精度分析

协方差分析理论是评估测量误差、观测几何以及考察参数等对解算参数精度影响的重要数学工具。Tapley最早将协方差分析理论应用于精密定轨技术的研究。本节基于协方差分析理论分别计算基于深空站测距、测速数据，以及融合测距、测速、时延数据进行定轨计算，解算得到位置速度协方差。分析仅考虑观测误差及观测几何对轨道精度影响，评估DVN单基线时延的引入对观测几何的改善能力。

图9为上述15组算例对应的协方差分析结果。转移阶段DVN单基线时延的融合使用，可以大幅改善观测几何，形式误差有近1倍的提升；环月阶段，单基线的融合使用，虽然观测几何有一定改善，但从形式误差的表现，改善非常有限，一般不足10%，该结论与实测数据分析一致。

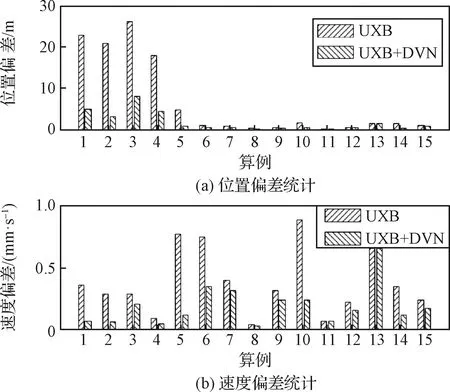
图9 形式误差统计Fig.9 Statistics of formal error

4 结 论

对嫦娥五号任务DVN时延数据进行处理，利用CVN与UXB数据解算的精密轨道对DVN时延数据的系统偏差进行标校，进一步分析DVN时延数据的引入对探测器观测几何的改善和定轨能力的提升,结论如下：

1)受限于测控系统跟踪模式，DVN时延数据无法充分利用射电源跟踪进行系统偏差的标校，采用稀疏交替射电源标校技术后仍然存在最大约1.4 m的系统差。

2)对于转移飞行阶段，由于观测几何的原因，单独利用UXB数据仅能实现千米级的轨道精度，DVN时延数据融合使用可以提升轨道精度近1倍，约为500～1000 m，若能标校残余的系统偏差，可以实现优于500 m的轨道精度。

3)对于环月飞行阶段，单独利用UXB数据可以实现优于百米的轨道精度，DVN单基线时延数据的引入不会明显改善定轨精度，由于系统偏差的存在可能在一定程度上降低定轨精度。

4)基于协方差分析，DVN时延数据的引入对于转移阶段可以显著改善观测几何，降低了形式误差，但对于环月飞行阶段，形式误差的提升有限，与实测数据的处理结论一致。