基于强化学习的大规模天线阵天线选择算法

柴新新刘 建

(中国船舶集团有限公司第八研究院,江苏 扬州 225101)

0 引言

以用户为中心的大规模多输入多输出(UCMMIMO)系统被视为能够应对5G 时代移动通信的庞大移动流量、低延时、高能效和高成本效率需求的关键技术。由于接入点天线数量大幅增加,传统天线选择算法不再能够应对。由此,研究人员对天线选择问题展开了广泛研究。

针对天线选择问题,实验证明,信号强度随着信号传播距离的增大而减小。所以根据用户分布的时间特性、不平衡性,对通信质量的需求不同等原因,系统内的天线不需要全部都处于工作状态,而仅是选择出部分天线执行信号收发任务即可。对于多输入多输出(MIMO)系统,基于穷搜的天线选择方法被广泛使用,但是在Massive MIMO 中,穷搜方法的计算复杂度就会达到不可忍受的地步。

基于凸优化和优势子矩阵搜索的方法计算复杂度也会随着天线数量的增多而增大。为了降低计算复杂度,一个贪婪搜索算法被提出,虽然计算复杂度较低,但此方法只能获得次优解。

对于Massive MIMO系统,基于信道矩阵的范数和相关性的两步选择方法也被提出,取得了较好的效果,但是这个方法是基于完备信道状态信息(CSI)的。不依赖于完备CSI的天线选择方法会造成较大的容量损失。研究人员也尝试使用机器学习算法解决天线选择问题,他们将天线选择问题建模为一个分类问题,但此做法不适用于UC-MMIMO。

综上,大多数传统天线选择算法都依赖完备CSI的获取,不依赖完备CSI的算法会导致较大的容量损失。而现实问题是,超大型天线阵列的完备CSI通常是不可得的。所以,如何在非完备CSI情况下进行天线选择成为了亟待解决的问题。

近年来,机器学习技术蓬勃发展,强化学习作为机器学习技术的一部分,对解决通信系统的自动探索、自决策、自组织、自优化问题都有着极大的帮助。本文率先将强化学习引入到天线选择问题中,与基于常规机器学习方法的工作不同的是,本文将天线选择问题建立了一个新的问题模型,仿真结果表明所提算法在非完备CSI情况下依然表现良好,并且在复杂度上也优于传统算法。

1 系统模型

本文考虑一个UC-MMIMO 场景如图1所示,其中天线数量为,用户数量为。≫,则接入点天线和用户的信道系数g ,可以表示为:

图1 UC-MMIMO 系统拓扑图

式中:,为接入点天线和用户的大尺度衰落系数,考虑了路径损耗和阴影效应,而且变化缓慢;h 为接入点天线和用户的小尺度衰落系数。

本文采用COST Hata模型,对大尺度衰落系数可以被表示为:

式中:σ=8 d B,表示阴影衰减偏差;z ～N(0,1);d 表示第个接入点天线与第个用户之间的距离;常有,是固定值,会在参数中提到;为子载波频率,单位表示为MHz;h 表示接入点天线高度,单位为m;h 表示用户天线高度,单位为m。

经分析,分布式Massive MIMO 系统中收发天线之间有直射路径,是莱斯信道。第个用户与第个接入点天线之间的小尺度衰落信道元素可以表示为:

式中:K 表示第个用户与第个接入点天线之间的莱斯因子;h～CN(0,)表示信道的非直射径分量;h表示直射径分量,可以表示为:

式中:表示接入点天线间距;表示波长;θ∈(-π/2,π/2),表示第个用户与第个接入点天线之间的到达角。

为了便于分析且不失一般性,天线间距假设为波长的一半,即/2。为了方便起见,本文将莱斯因子设定为6。

本文使用共轭波束成形技术将信号发送给用户,可知第个接入点天线传输的信号可以表示为:

式中:φ,1,…,为发射信号,{|φ|}1;为每个传输信号的正则化后的信噪比(SNR);η为能量分配系数。

则第个用户接收到的信号被表述为:

式中:z 代表第个用户的高斯白噪声。

而第个用户的可到达率可被表示为:

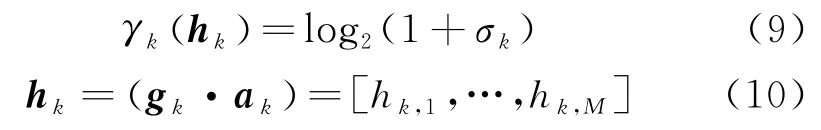
式中:h 为与第个用户相连的所有天线信道系数组成的向量;g 为第个用户和所有个接入点天线的信道系数组成的信道向量;a 为第个用户和所有个接入点天线的连接状态,元素为1表示两者处于连接状态,为0表示两者处于断开状态。

第个用户的信干噪比(SINR)为:

2 天线选择问题建模

在移动通信系统中,当用户设备在通信过程中从一个基站覆盖区移动到另一个基站覆盖区,或者由于外界干扰而造成通信质量下降时,必须改变原有信道而转接到空闲信道上去,以继续保持通信的过程。但是由于分布式Massive MIMO 系统特点导致移动中的用户频繁切换接入点天线。在切换过程中,系统中海量数据的传输与处理工作以及信令开销均大幅增加,导致较大的传输能耗和计算能耗。但是假如当前接入点天线能够满足新位置的通信需求,则没必要被重新分配接入点天线的。

为此,本文设定了用户容量阈值。只有当前连接的接入点天线带来的容量γ小于时,系统才会为用户重新选择接入点天线,适当增大或减小容量阈值γ可以调整容量和能耗之间的tradeoff关系。为了不失一般性,规定了每个用户最多只能连接个接入点天线。

由于接入点天线能量的有限性,设置了每个接入点天线的最大用户连接数为,当天线服务用户人数等于时就不能为额外用户服务了,此类接入点天线被称为“满载天线”。则整个优化问题可被整理为:

式中:第1个约束表示当前容量和容量阈值之间的大小关系,第2个约束表示为每个接入点天线用户连接数目限制,第3个约束表示每个用户的接入点天线连接数限制,第4个约束表示每个接入点天线的用户连接数,第5个约束表示每个用户的接入点天线连接数,第6个约束表示第个接入点天线和第个用户之间的连接状态。

由于优化问题是个NP-hard问题,强化学习方法作为求解NP-hard问题的有力工具,被很多研究人员广泛采用,本文也采用此方法求解NP-hard问题。

3 基于A3C的天线选择算法

强化学习方法是以马尔可夫决策过程为基础的。在本文中,使用A3C算法解决UC-MMIMO 系统中的天线选择问题。A3C(multi-threaded asynchronous advantage actor-critic)被称为策略-评论家算法中的一种,可以有效地利用计算机资源,提升训练效用,成倍提高运行速度,并且有利于减少数据之间的相关性,有利于程序收敛。首先需要将其转化为马尔科夫决策过程,需要定义状态空间、动作空间和奖励机制。

状态空间:为了降低对CSI的依赖,本文采用用户位置作为输入,为了避免产生过大的状态空间,本文将区域进行栅格化划分,将每个栅格的坐标视为其重心坐标,用户的坐标被视为栅格坐标。则状态空间元素可被表示如下:

式中:l []为此用户在第个时间节点的轴坐标;l []为此用户在第个时间节点的轴坐标。

动作空间:因为解决的是天线选择问题,所以本文定义的动作空间的每个元素都是一个天线组合。根据用户连接接入点天线数量限制,系统需要为每个用户选择个天线,则本文将动作空间设定为一个列的行向量,向量元素由0或者1组成,元素为1的数量等于。元素等于1表示此用户与该天线连接,否则表示断开。则动作空间的每个元素可被表示如下:

奖励机制:本文的优化目标是最大化一段时间内用户总容量,因此奖励机制应被设置为所选天线为用户带来的瞬时容量。但瞬时容量的计算和被选择天线组合中的满载天线相关。当被选择的接入点天线都不满载时,将此时的容量设定为即时奖励,即时奖励可被表示为:

式中:[]表示用户在第个时间节点的即时奖励;σ表示用户在第个时间节点的信干噪比。

当选择到满载天线时,将给予惩罚,惩罚被设定为一个负值。因为本文设定的目标函数是长期时间内的容量最大化,则长期奖励被表示为:

式中:为折扣因子,表示对未来奖励的重视程度。

根据定义的状态空间、动作空间和奖励机制,优化问题被转化为了马尔可夫决策问题,它可以被强化学习算法求解。被转化后的问题可以表示为:

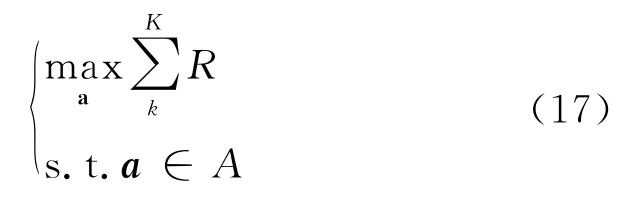
然而,在某些情形下,模型不可避免地会选择到满载天线,满载天线并不能为用户提供通信服务,需要对选择的天线进行调整。为此,本文基于最近距离原则设计了天线调整机制。其设计思想是当满载天线被选择后,系统根据用户的位置选择距其最近的几条非满载天线替换掉满载天线,替换天线的数目等于为此用户分配的满载天线数量。

本文采用最大欧几里得范数天线选择算法和两步选择算法作为对照算法。为了公平性,所提算法和对照算法均采用相同的系统模型、环境配置和参数设置,并且也将其改成以用户为中心的形式。下面对对照算法进行简要概述。

(1) 两步选择算法:顾名思义,此算法是根据其原理经过两次筛选才最终选定服务天线的天线选择算法。在第1步选择中,此算法根据空间相关性从全体天线中选出N 个备选天线;在第2步中,通过最大化奇异值从N 个备选天线中选择出N 个天线作为最终选定的天线。

(2) 最大欧几里得范数选择算法:对于每个用户,此算法通过对所有天线对此用户的信道系数求解欧几里得范数并排序,选择最大的几根天线。的配置如表1所示。

表1 仿真参数表

首先,本文对比了所提算法和2个对照算法的算法复杂度。所提算法由选择阶段和调整阶段组成,则算法复杂度也由两部分构成。选择阶段的复杂度可被表示为(),第二阶段的复杂度为(),因此所提算法的总算法复杂度为((1))。最大欧几里得范数选择方法的复杂度为()。所提算法和最大欧几里得范数选择算法的复杂度大小仅与用户数和天线数量相关,当用户数量和接入点天线数量都确定后,其复杂度也随之确定。

4 仿真分析

本文考虑了一个1 km×1 km 的正方形区域,个用户和个接入点天线随机分布,区域被划分为多个20 m×20 m 的子区域。本文仿真时各参数因此,随着N 的增长,两步选择算法的复杂度会急剧增长,当N 增加时,算法复杂度缓慢增加,达到最高点时,如果N 继续增加,算法复杂度会以同样的速度缓慢下降。而N 才是影响两步选择算法复杂度的主要因素,因为在第2步选择中,算法需要遍历所有天线组合的奇异值。当N 增大时,天线组合数量会急剧增加,导致算法复杂度同样急剧增加。

值得一提的是,因为两步选择算法有2个自变量,分别是第1步选择天线数量和第2步选择天线数量。对算法复杂度产生最大影响的是第1步选择的天线数量,所以不能将3个算法的复杂度用1 张图表示,而是需要用2 张图进行表示。对比图如图2所示,本文设定用户人数=6,接入点天线数目=105,第1步选择出的备选接入点天线数目N =10,第2 步选择出的接入点天线数目N =5。

图2中,最大欧几里得范数算法的复杂度略微小于两步选择算法,两步选择算法的复杂度随着第1步选择数目的增加而呈指数增长,并且其单位的数量级远远大于所提算法和最大欧几里得范数算法的复杂度的数量级。可知,所提算法在计算复杂度上相较于传统算法占有优势。

图2 算法复杂度对比图

在表2中,本文给出了3 种算法的运行时间。两步选择算法运行时间是最长的,且远高于其他2个算法。两步选择算法和最大欧几里得范数天线选择算法均不需要事先训练,而所提算法需要事先进行30 min的训练,但这个训练时长是可接受的。

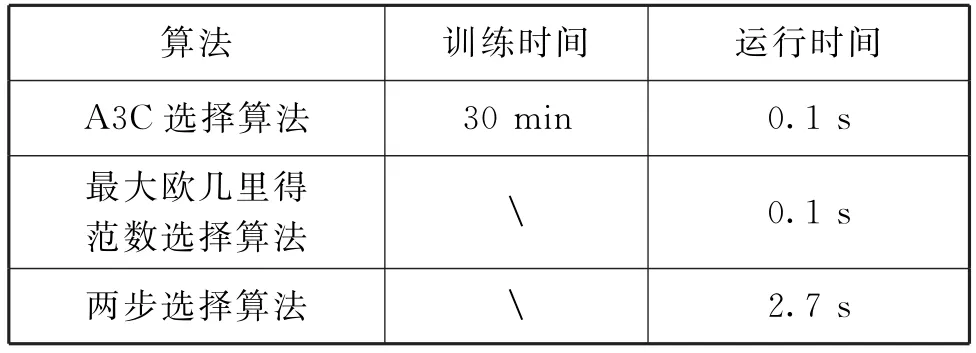
表2 算法运行时间表

当完备的CSI可以获得时,设定第1次选择出的备选接入点天线N 数量为10,变化最后选择出的接入点天线数量、系统容量对比图如图3 所示。两步选择算法取得了最高的系统容量,最大欧几里得范数算法的取得效果总体弱于两步选择算法,但是相差无几,所提算法略低于2个对照算法。

图3 系统容量在完备CSI下的影响图

一个可信的解释是本文提出的基于强化学习的天线选择算法不能利用CSI信息,从环境中获得的信息最少,所以性能差于2种对照方案;3种算法随着选择的接入点天线数量的增大而先增大后减小,这可以解释为干扰信号的增长速度超过了有用信号的增长速度。

在传输端仅可知大尺度CSI,一个天线选择和波束成形算法被提出用以最小化能量损耗。受此论文启发,本文采用类似方法,探索小尺度衰落信息不能获取时的系统容量变化,如图4所示。

图4 系统容量在非完备CSI下的影响图

同样,设置N =10,可以看出,依赖于CSI信息的两步选择算法和最大欧几里得算法的容量下降剧烈。当CSI信息不完备时,此算法已经不能有效地解决天线选择问题了。而本文所提出的算法由于不依赖于CSI,所以性能没有变化。可以得出结论,本文所提算法在CSI不可得时,依然表现良好。

5 结束语

本文提出了一种基于A3C 算法的天线选择算法,为了进一步提高算法性能,提出了基于最近距离算法的天线调整机制。为了证明所提算法在性能方面的优势,选择了2个传统天线选择算法作为对照方案。

通过此3种算法仿真结果表明:在完备CSI情况下,所提算法性能劣于传统算法,但性能差距不大;在非完备CSI情况下,传统算法的性能大幅下降,而所提算法性能变化不大,且远优于传统算法。除此之外,所提算法在算法复杂度上也有较大优势。证明所提算法可以在UC-MMIMO 系统中有效解决天线选择问题。