二维过渡金属磷化物MnTn+1(M = V, Cr; T = P, As, Sb)的第一性原理计算研究

张亚琼 谢文辉

摘要： 采用基于密度泛函理论的第一性原理计算 ， 研究了二维过渡金属磷系化合物 MnTn+1（M = V， Cr; T = P， As， Sb）材料的結构、稳定性、电子结构和磁性质. 通过计算形成能和声子谱 ， 发现只有 V4As5、 Cr2P3、 Cr3P4、 Cr4P5、 Cr2As3和 Cr3As4是稳定的二维磁性多层膜. 计算结果表明 ， 这些稳定的二维磁性材料都是反铁磁金属. 此外 ， 还对这些材料的电子结构和磁耦合机制做了进一步的分析.

关键词：第一性原理计算;  二维材料;  磁性;  自旋电子学

中图分类号： O469    文献标志码： A    DOI： 10.3969/j.issn.1000-5641.2022.02.010

First-principles calculations investigations of two-dimensional transition metal phosphide MnTn+1（M = V， Cr; T = P， As， and Sb） slices

ZHANG Yaqiong，  XIE Wenhui

（School of Physics and Electronic Science， East China Normal University， Shanghai  200241， China）

Abstract： In this paper， the  atomic structure， stability， electronic structure，  and magnetism of two- dimensional transition metal phosphide MnTn+1（M = V， Cr; T = P， As， and Sb） slices were systematically studied  using  the  first-principles  calculations  based  on  density  functional  theory. By  calculating  the formation energy and phonon spectrum， it was determined that only V4As5 ， Cr2P3 ， Cr3P4 ， Cr4P5 ， Cr2As3 ， and Cr3As4 are stable two-dimensional magnetic multilayers. The results show that these stable two- dimensional magnetic materials are antiferromagnetic metals. In addition， the electronic structure and the magnetic coupling mechanism of these materials were further analyzed.

Keywords： first-principles calculations;  two-dimensional materials;  magnetism;  spintronics

0  引言

二维磁性材料的研究对下一代自旋电子学器件的研发极为重要 ， 因此得到了相关科研人员的广泛关注.2017年 ， 实验上第一次在 CrI3和 Cr2Ge2Te6这两种范德瓦尔斯材料中证实了二维铁磁性的存在[1-2] ， 这立即激发了科研工作者对二维范德瓦尔斯磁性薄膜的研究兴趣.随后 ， 二维过渡金属硫化物 MT2（T = S， Se， Te）、二卤化物 MX2（X = Cl， Br， I）、三卤化物 MX3（X = Cl， Br， I）、MBT3（B = Si， Ge， Sn）和 Fe3GeTe2等多种二维范德瓦尔斯磁性材料被实验报道[3-11]. 在理论计算方面 ， 基于密度泛函理论（Density Functional Theory ， DFT）的第一性原理计算 ， 进一步扩展了二维磁性材料的种类 ， 如过渡金属氮化物、碳化物或碳氮化物组成的 MXene 系列[12-14] ， 二维过渡金属磷化物 MT （T = P， As）和二氢化物 MH2（M = Co， Sc）单层膜中均存在铁磁性[15-17]. 此外 ， 运用基于大型晶体数据库的高通量计算和机器学习方法 ， 也挖掘出许多二维磁性材料[18-19]. 目前对二维磁性的研究依然在不断深入 ， 发现新的二维磁性材料并深入研究其性质是一个重要课题.

大多数二维磁性膜有类似三明治的结构：1 个过渡金属原子层的两边夹着磷族、硫族或卤族原子层. 通过掺杂、外加门电压、堆叠构建二维范德瓦尔斯超晶格、异质结等方法可以调控磁性[20-21]. 另外， 也可以通过在二维晶格中加入更多金属原子层的方法来改善磁性. 据实验报道 ， 在二维 Fe3GeTe2中加入两层铁原子可以形成二维 Fe5GeTe2磁性膜 ， 并能够显著提高其居里温度[22]. 基于同样的思路 ， 本文利用基于密度泛函理论的第一性原理计算 ， 系统地研究了具有多个过渡金属层（n）的二维过渡金属磷化物 MnTn+1（M = V， Cr; T = P， As， Sb; n =2， 3， 4）的性质. 由于较厚的多层膜（n >4）的性质更接近于块体 ， 所以本文重点研究了 n =2， 3， 4的情况 .结果表明 ， V4As5、Cr2P3、 Cr3P4、 Cr4P5、 Cr2As3和 Cr3As4是稳定的二维反铁磁金属 ， 有望被应用于自旋电子学器件中.

1  计算方法

本文计算方法采用的是基于密度泛函理论（DFT）的赝势平面波法 ， 使用 VASP （Vienna Ab-initio Simulation Package）程序包并采用 Projector Augmented-Wave （PAw）方法[23] ， 交换关联函数采用 Perdew-Burke-Ernzerhof （PBE）广义梯度近似（Generalized Gradient Approximation， GGA）[24]. 由于过渡金属中的关联电子效应 ， GGA 近似往往不能准确地描述其电子结构和磁性， 故采用计入 Hubbard 修正的 GGA + U （Hubbard 参数）方法[25-26]. 根据前人工作 ， V 和 Cr 的 U 值分别取3 eV 和2.6 eV， 这些 U 值被证实能较好地描述类似化合物的性质[27-28]. 在计算中 ， 平面波截止能量（Energy Cutoff， ENCUT）均设定为400 eV， 真空层设置为 15 Å 来模拟二维体系;布里渊区积分采用 Monkhorst- Pack 方法[29] ， 并将取样网格设为20× 20× 1;体系的能量收敛判据均设定为1 ×10–6 eV， 优化结构和原子位置的收敛判据是每个原子上的力小于0.01 eV/Å;此外 ， 使用 Phonopy 程序 ， 基于超胞方法计算声子谱[30-31].

2  结果与讨论

2.1  二维 MnTn+1多层膜的晶体结构

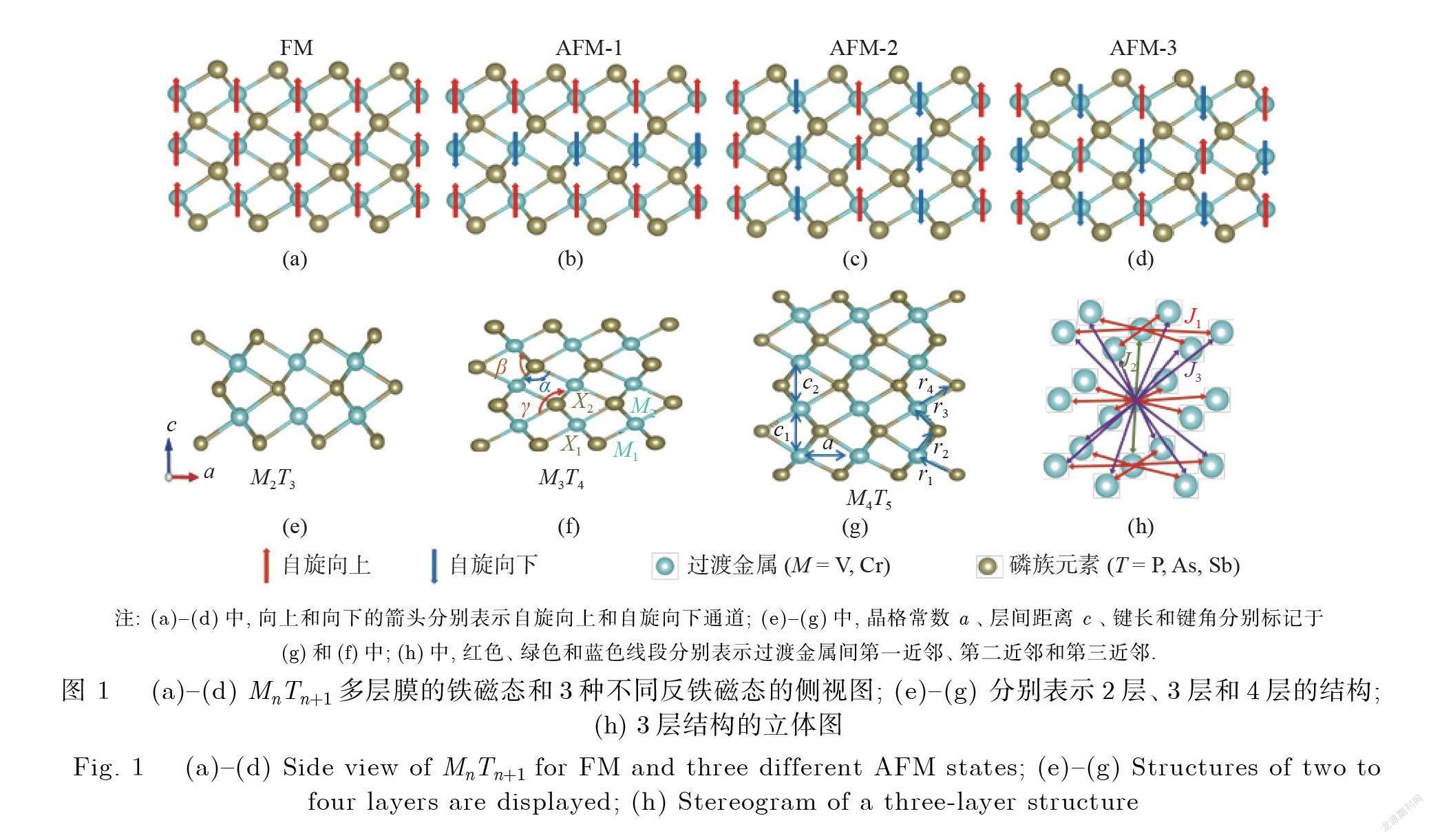
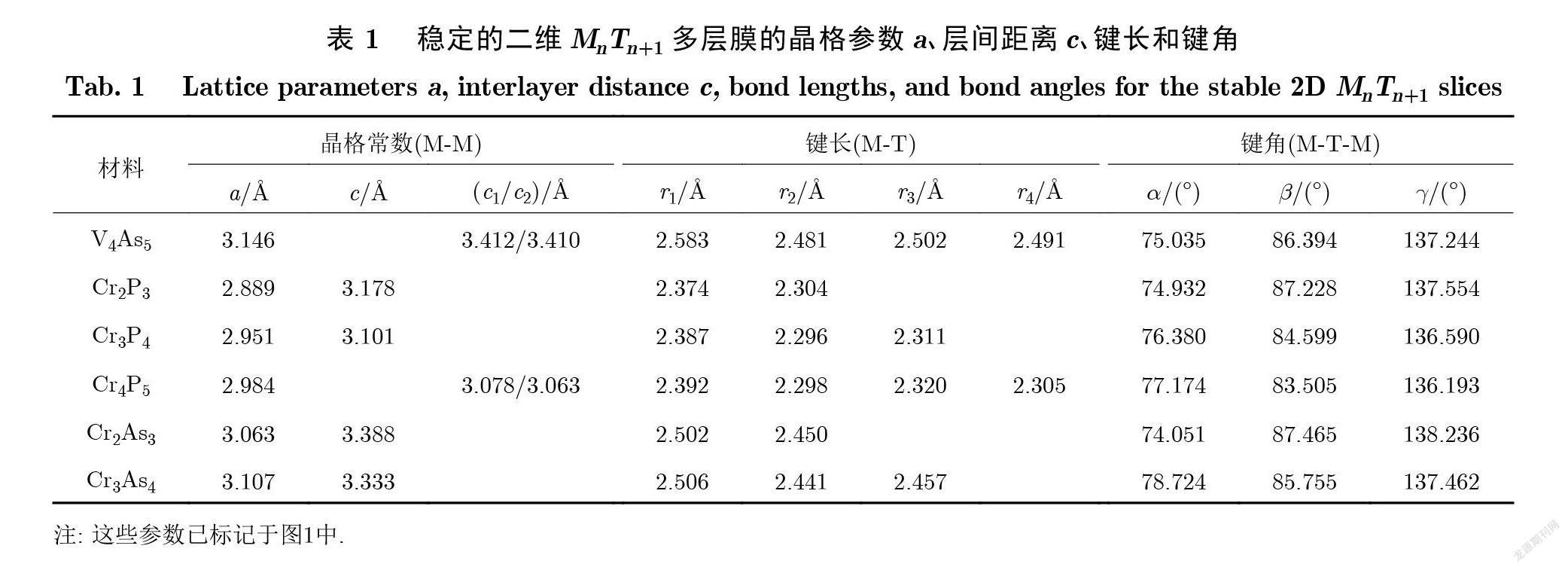
首先讨论过渡金属磷化物多层膜的晶体结构和晶格参数. 如图 1所示 ， 二维 MnTn+1薄片包括 n 层过渡金属（M）和 n +1 层磷族元素（T）. MnTn+1多层膜具有两个“外层”金属（磷族）层和 n –2 个“内层”金属层（或 n –1 个内层磷族层）.由过渡金属原子（M）和配位的磷族元素（T）构成的 MT6八面体沿 z 轴方向上共面 ， 过渡金属占据八面体中心位 ， 整体具有六角对称性. 计算得到的二维 MnTn+1多层膜的结构参数在表 1中列出 ， 其中 ， 晶格参数 a 描述的是平面内六角晶格的原子间距;参数 c 为金属层之间的垂直距离 ， 即沿 z 方向过渡金属原子间的键长. 如图 1（g）所示 ， 对于 n =2，3的多层膜 ， 只有1 个 c 参数;而当 n =4 时 ， 则有2 个 c 参数 ， 分别标注为参数 c1和参数 c2 ， 前者为外层金属与内层金属之间的间隔 ， 后者为两内层金属之间的间隔. 图 1中 ， FM （Ferromagnetism）表示铁磁态 ， AFM （Antiferromagnetism）表示反铁磁态. 表 1中给出了 M-T-M 间的角度 ， 层间最近邻金属原子间的键角 b 轻微地偏离90°， 而层内金属原子间的键角 a 和层间次近邻金属原子间的键角 g 分别轻微地偏离75°和135°， 其中 a、 b 和 g 已标于图 1（f）中.

2.2  二维 MnTn+1多层膜的稳定性

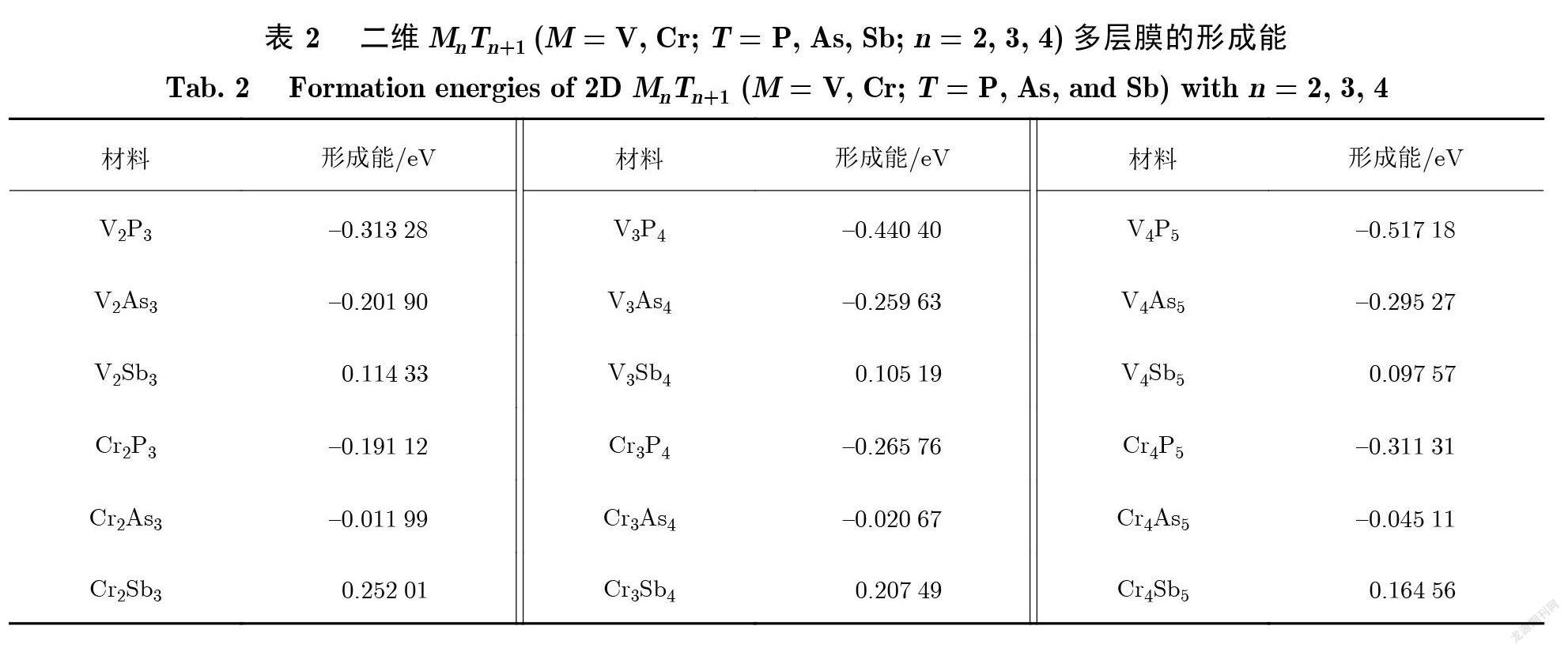
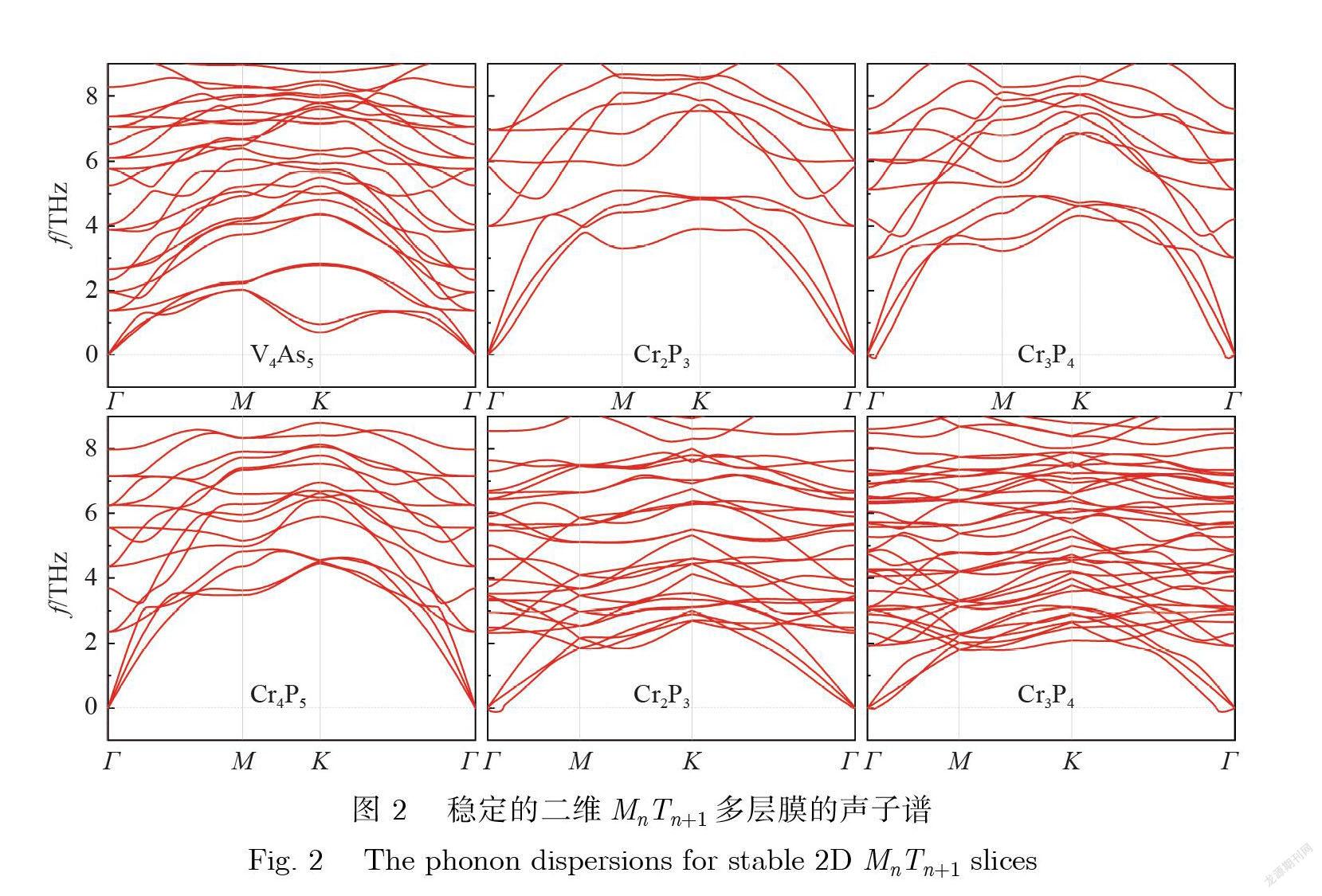
为了研究二维 MnTn+1多层膜的稳定性 ， 本文采用 PBE 泛函计算了形成能和声子谱. 形成能 （Eform）由二维材料的基态总能减去对应元素块体相的总能得到 ， 即 Eform = E2D – nEM –（n +1）ET ， 其中 ， E2D、 EM 和 ET 分别是 MnTn+1多层膜能量、 M 块体相能量和 T 块体相能量 ， 详见表 2.二维多层膜的基态对应于图 1中所示的铁磁和几种反铁磁构型的能量最低态. 从表 2可以看出 ， P 系列和 As 系列化合物的形成能均为负值 ， 而 Sb 系列化合物的形成能为正值 ， 这说明只有 P 系列和 As 系列化合物才有可能稳定存在.另外 ， 本文通过声子色散曲线是否有虚频来检验其动力学稳定性.稳定化合物沿 G（0，0，0）–M（1/2，0，0）–K（1/2，1/2，0）–G（0，0，0）的声子谱如图 2所示 ， 其中 ， 纵坐标为频率（f）.由图2可知 ， 大部分 V 系列化合物的声子谱有虚频 ， 只有 V4As5多层膜没有虚频;在 Cr 系列化合物中 ， Cr4As5的声子谱有明显虚频 ， Cr2P3和 Cr4P5完全没有虚频 ， 而 Cr3P4、C2As3和 Cr3As4的声子谱只是在 G点附近显示出很轻微的虚频 ， 因此有可能依靠衬底而存在.

2.3  二维 MnTn+1多层膜的电子结构

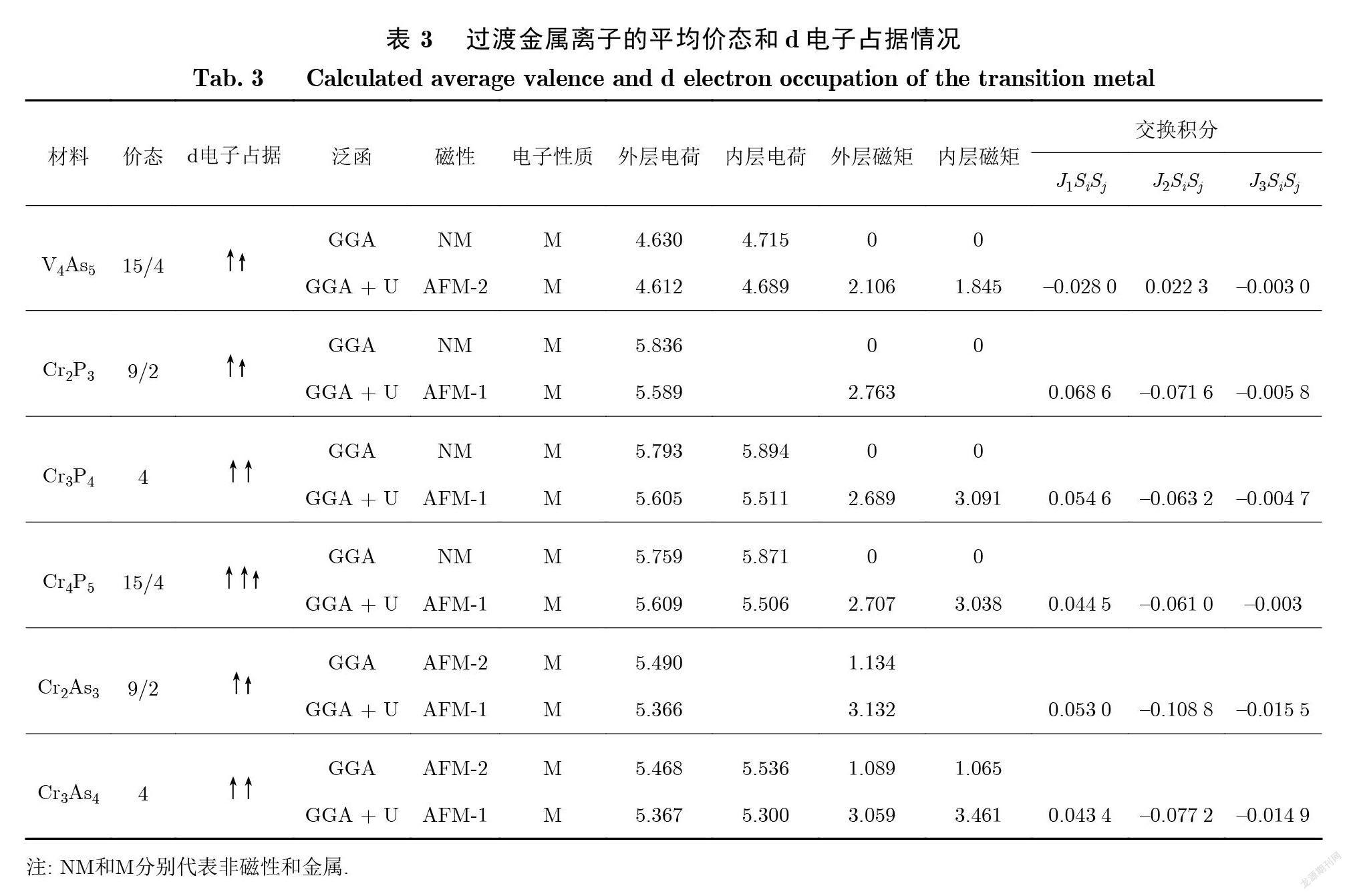
现在进一步探讨二维 V4As5、Cr2P3、Cr3P4、Cr4P5、Cr2As3和 Cr3As4多层膜的电子结构. 由前文对结构的分析可知 ， 对于 n >2 的多层膜 ， 内外层不等价 ， 内层和外层的金属离子呈现不同的化合价;而对于 n =2 的多层膜 ， 两个金属层是等价的.从离子模型出发 ， 对于两层结构的 Cr2P3和 Cr2As3 ， 可以认为金属离子的化合价均为+ 9/2;而对于 n >2 的多层膜 ， 比如 Cr3P4、Cr4P5、Cr3As4和 V4As5多层膜 ， 内外金属层电荷分布则不平衡 ， 这与只有单金属层或双金属层的二维 MT2和 M2 T3是不同的. 如果认为金属层完全被离子化 ， 则外层过渡金属的价态应为+ 9/2价 ， 而内层应为+ 3价.如果假设内层和外层离子之间没有电荷转移 ， 那么内层和外层过渡金属的化合价类似 ， 接近于3 +3/n.考虑到强的 p-d 共价成键 ， 实际的电荷分布应该介于这两者之间. 表 3给出了内层和外层金属离子的电荷数. 由表 3可以看到， 电荷数差距很小 ， 说明电荷转移较弱.

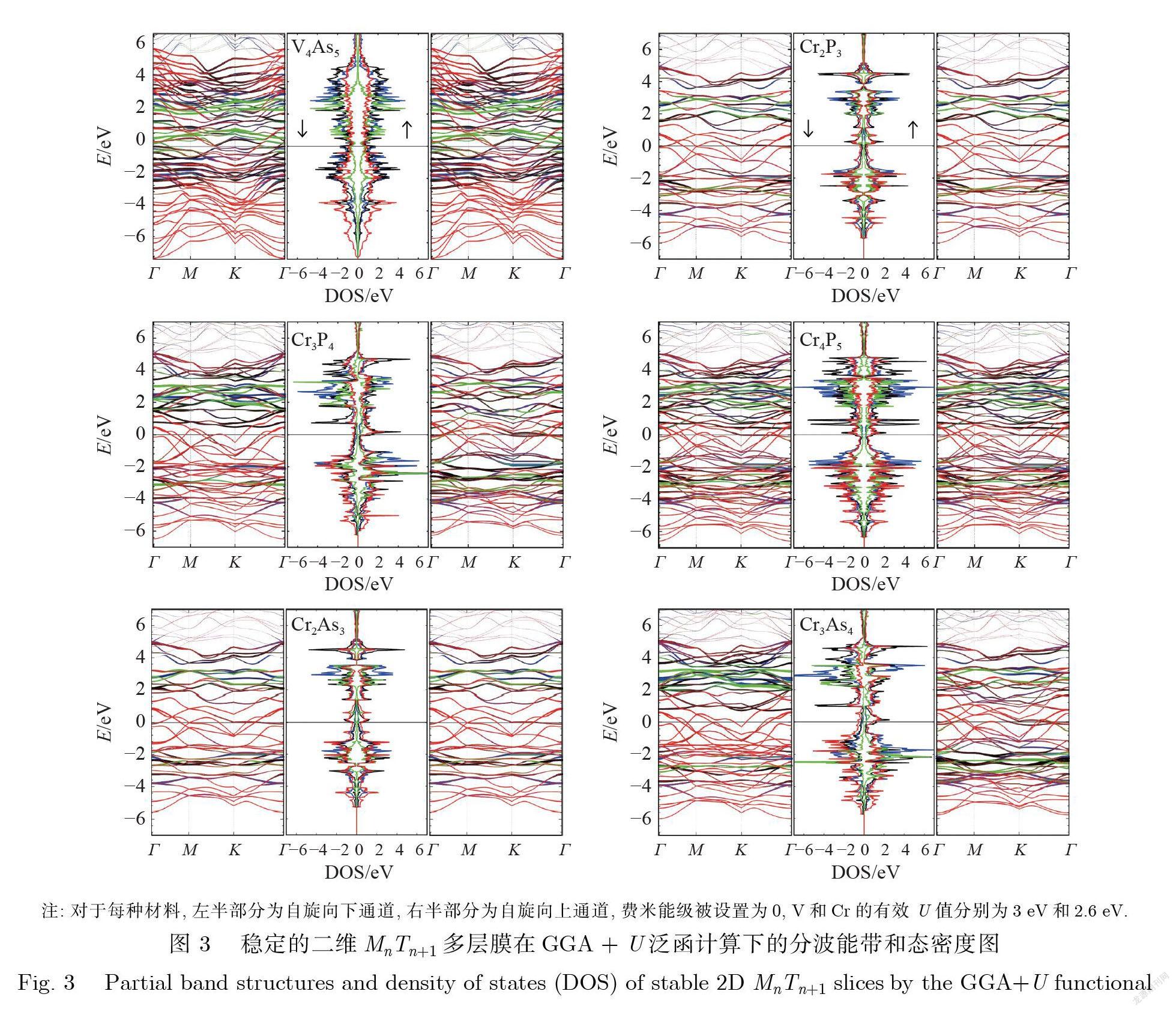
图 3为采用 GGA + U 泛函计算得到的原子轨道投影的能带（E）和态密度（Density of States， DOS）图 .由图3可以看出 ， –2 eV 左右的能級为过渡金属3d 轨道和磷族元素 p 轨道的成键态 ， 强的 p-d 轨道成键将 p 轨道推得很深;而 2 eV 附近为以过渡金属3d 态为主的反键态 ， 最终这些稳定化合物都表现为金属导电性.下面进一步分析电子结构. 由于过渡金属离子处于八面体环境， 5个 d 轨道劈裂为 t2g 和 eg 态 ， 并进一步被三角晶场分裂为单重简并的 a1g （dz2）态和二重简并的 e1（dxz; dyz）和 e2（dxy;dx2    dy2） 态. 此外 ， 不对称的 M-T键会进一步降低体系对称性 ， 导致 e1和 e2态去简并 ， 但是这个不对称性的影响很小.需要指出的是 ， 在 PBE计算中 ， 也同样得到了金属特性的能带 ， 只是对应的磁交换能较弱 ， 而 PBE + U 计算给出了更大的磁矩值. 从能带图中可以看出 ， 由于电子关联所引起的附加磁交换能量 ， 过渡金属的 d 轨道能级会被推得很深.此外 ， 内外层的原子在能带图中没有表现出明显的分布差异 ， 没有出现因为电荷不平衡导致的层依赖的轨道特性.结合表3中内外层较小的电荷和磁矩差异 ， 可以看出这类化合物的共价成键而非离子成键的特性.

2.4  二维 MnTn+1多层膜的磁性

下面对稳定化合物的磁性进行研究.首先 ， 通过比较图1中所示的铁磁态和3 种反铁磁态的总能 ， 得到 MnTn+1多层膜的基态;然后采用 GGA 泛函和 GGA + U 泛函分别计算得到磁性、电子性质、内外层金属离子的电荷和磁矩 ， 以及过渡金属元素第一近邻、第二近邻、第三近邻间的交换积分. 结果详见表3.由表3中列出的金属离子的磁矩 ， 可以发现金属离子均处在高自旋态 ， V 的磁矩大约是2 µB ， Cr 的磁矩大约是3 µB.在 MnTn+1多层膜中 ， 因为内外层电荷不平衡较小 ， 故磁矩变化也较弱. 如前文中所提到的 ， 采用 GGA 泛函和 GGA + U 泛函的计算结果有明显不同：在基于 GGA 的计算中 ， V4As5、Cr2P3、Cr3P4和 Cr4P5是非磁性的 ， Cr2As3和 Cr3As4为 AFM-2型磁基态; GGA + U 计算结果显示 ， V4As5为 AFM-2型磁基态 ， Cr 系列化合物均为 AFM-1型磁基态 ， 即层内为铁磁有序 ， 而层间为反铁磁有序.这些结果表明电子关联效应对 MnTn+1多层膜的性质影响较大.故本文研究采用不同 U 值（2～ 5 eV）对材料磁基态的影响. 铁磁态与反铁磁基态的能量差（EAFM – EFM）如图 4所示. 由图 4可知， 随着 U 值的增加 ， 过渡金属磷化物的磁基态没有改变.

下面讨论二维 MnTn+1多层膜对应的磁性微观机制.计算表明 ， V4As5是层间铁磁有序 ， Cr 系列化合物为层间反铁磁有序. 本文采用基于局域磁矩的海森堡模型来简单分析其磁相互作用. 相应公式为

H =   Ji;jSi    Sj ，

其中 ， H 为哈密顿量 ， Si、 Sj分别代表 i 位、 j 位的磁矩 ， Ji，j代表 i 位、 j 位点间的交换耦合常数. 如图1（h）所示 ， 考虑第三近邻交换耦合作用 ， 用 J1、 J2和 J3分别代表第一近邻、第二近邻和第三近邻交换耦合常数; J1为层内耦合作用， J2和 J3为层间耦合作用.通过将此模型应用到第一性原理计算中， 可以得到交换系数 J 的值. 本文中的 J1、J2和 J3可以从图 1所示的4 种不同磁构型的总能中得到.下面以 Cr3P4为例进行分析 ， 4种不同磁构型的总能可以表示为

得到的交换积分列在表3中 ， 正值和负值分别表示铁磁和反铁磁相互作用.对于 Cr 系列化合物 ， 层内交换系数 J1均为正值 ， 而层间交换系数 J2和 J3为负值. 对于 V4As5 ， 层内交换系数 J1为负值 ， 层间交换系数 J2为正值 ， 而层间次近邻交换系数 J3为负值. 不管是 Cr 系列化合物還是 V4As5 ， 层间次近邻交换耦合系数 J3相对于 J1、J2强度均很微弱.对于 Cr 系列化合物 ， 层内倾向于铁磁相互作用 ， 而层间倾向于反铁磁相互作用 ， 故表现为 AFM-1型磁基态. 对于 V4As5 ， 层内倾向于反铁磁相互作用 ， 层间最近邻交换表现为铁磁耦合; 而第三近邻交换 J3虽表现为反铁磁相互作用 ， 但强度较小 ， 故 V4As5表现为 AFM-2型磁基态.

因为内层和外层金属离子间的电荷不平衡且很小 ， 内外金属层之间没有明显的电荷转移现象 ， 所以双交换模型贡献较小 ， 而超交换模型应当起主要作用. 根据 Goodenough-Kanamori-Anderson （GKA）理论规则[32-33] ， 如果 M-T-M 的键角接近于90°， 2个过渡金属的半满 d 轨道通过磷族元素 p 轨道的相互作用趋向于铁磁超交换耦合;如果 M-T-M 的键角接近于180°， 则半满 d 轨道间的超交换作用趋向于反铁磁耦合. 如图1（h）所示 ， 通过近邻的磷族阴离子 ， 第一近邻的平面内金属离子之间有6 条交换路径;而对于相邻层间第二近邻的垂直金属离子对之间 ， 其 d 轨道间也有3 条通过 M-T-M 键的交换路径 ， 对应的 M-T-M 键角接近于90°.此外 ， 垂直原子之间的距离比3 Å略大 ， 故 d 轨道间应当也存在由直接交换引起的反铁磁相互作用.直接交换和超交换间的竞争导致 V4As5的 J2是铁磁相互作用;而 Cr 系列化合物的层间最近邻交换则为反铁磁相互作用.从表1中可以看到 ， 最近邻金属离子之间的磁性耦合 J1对应的面内 M-T-M 键角都接近于75°， 因此面内的 d 轨道间的超交换相互作用应处在铁磁和反铁磁耦合之间 ， J1具体对应于哪种磁性耦合则依赖于实际材料. 通过计算得到 ， 对于 Cr 系列化合物 ， 层内相互作用皆是铁磁性的 ， 而 V4As5则表现为层内反铁磁性.第三近邻金属离子之间的 d 轨道超交换相互作用对应于层间交换耦合 J3 ， 对应的 M-T-M 键角在135°左右 ， 半满的 d 轨道相互作用趋向于反铁磁耦合.利用海森堡模型得到的交换相互作用参数 ， 可以通过超交换相互作用对应的耦合机制进行解释 ， 且较大的交换积分也意味着这些稳定的二维材料可能具有较高的居里温度.因此， 二维过渡金属磷系化合物 MnTn+1有潜力被应用于自旋电子学中.

3  结论

本文利用第一性原理计算的方法 ， 对二维过渡金属磷系化合物 MnTn+1（M = V， Cr; T = P， As，Sb）进行了研究. 通过形成能和声子谱计算 ， 得到了 V4As5、Cr2P3、Cr3P4、Cr4P5、Cr2As3和 Cr3As4是稳定的二维磁性多层膜. 在这些稳定的二维材料中 ， V4As5为 AFM-2型金属 ， 其余的 Cr 系列多层膜均为 AFM-1型金属. 本文还进一步讨论了稳定化合物的电子结构和磁性耦合机制.近年来 ， 反铁磁自旋电子学器件由于其在纳米电子学中的应用前景而受到越来越多的关注. 因此本文通过计算发现的这些二维磁性 MnTn+1多层膜非常有价值 ， 同时也期望其能够被进一步扩展到其他相似的二维磁性材料的研究中.

[參考文献]

[1]GONG C， LI L， LI Z L， et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals [J]. Nature， 2017， 546（7657）：265-269.

[2]HUANG B， CLARK G， NAVARRO-MORATALLA E， et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit [J]. Nature， 2017， 546（7657）：270-273.

[3]O’HARA D. J， ZHU T C， TROUT A H， et al. Room temperature intrinsic ferromagnetism in epitaxial manganese selenide films in the monolayer limit [J]. Nano Letters， 2018， 18（5）：3125-3131.

[4]BONILLA M， KOLEKAR S， MA Y J， et al. Strong room-temperature ferromagnetism in VSe2 monolayers on van der Waals substrates [J]. Nature Nanotechnol.， 2018， 13（4）：289-293.

[5]LI J， ZHAO B， CHEN P， et al. Synthesis of ultrathin metallic MTe2 （M = V， Nb， Ta） single-crystalline nanoplates [J]. Advanced Materials， 2018， 30（36）：1801043.

[6]SUN X， LI W Y， WANG X， et al. Room temperature ferromagnetism in ultra-thin van der Waals crystals of 1T-CrTe2 [J]. Nano Research， 2020， 13（12）：3358-3363.

[7]HUANG B， CLARK G， KLEIN D R， et al. Electrical control of 2D magnetism in bilayer CrI3 [J]. Nature Nanotechnology， 2018， 13（7）：544-548.

[8]JIANG S， LI L Z， WANG Z F， et al. Controlling magnetism in 2D CrI3 by electrostatic doping [J]. Nature Nanotechnology， 2018， 13（7）：549-553.

[9]LIU H， WANG X S， WU J X， et al. Vapor deposition of magnetic van der Waals NiI2 crystals [J]. ACS Nano， 2020， 14（8）：10544-10551.

[10]LIU Y， WANG W， LU H Y， et al. The environmental stability characterization of exfoliated few-layer CrXTe3 （X=Si， Ge） nanosheets [J]. Applied Surface Science， 2020（511）：145452.

[11]DENG Y， YU Y J， SONG Y C， et al. Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2 [J]. Nature， 2018， 563（7729）：94-99.

[12]KHAZAEI M， ARAI M， SASAKI T， et al. Novel electronic and magnetic properties of two-dimensional transition metal carbides and nitrides [J]. Advanced Functional Materials， 2013， 23（17）：2185-2192.

[13]KUMAR H， FREY N C， DONG L， et al. Tunable magnetism and transport properties in nitride MXenes [J]. ACS Nano， 2017， 11（8）：7648-7655.

[14]HU Y， LIU X Y， SHEN Z H， et al. High Curie temperature and carrier mobility of novel Fe， Co and Ni carbide MXenes [J]. Nanoscale， 2020， 12（21）：11627-11637.

[15]WANG B， ZHANG Y H， MA L， et al. MnX （X = P， As） monolayers a new type of two-dimensional intrinsic room temperature ferromagnetic half-metallic material with large magnetic anisotropy [J]. Nanoscale， 2019， 11（10）：4204-4209.

[16]MOGULKOC A， MODARRESI M， RUDENKO A N. Two-dimensional chromium pnictides  CrX （X = P， As，  Sb）： Half-metallic ferromagnets with high Curie temperature [J]. Physical Review B， 2020， 102（2）：024441.

[17]WU Q， ZHANG Y H， ZHOU Q H， et al. Transition-metal dihydride monolayers： A new family of two-dimensional ferromagnetic materials with intrinsic room-temperature half-metallicity [J]. Journal of Physical Chemistry Letters， 2018， 9（15）：4260-4266.

[18]ZHU Y， KONG X H， RHONE T D， et al. Systematic search for two-dimensional ferromagnetic materials [J]. Physical Review Materials， 2018， 2（8）：081001.

[19]LU S， ZHOU Q H， GUO Y L， et al. Coupling a crystal graph multilayer descriptor to active learning for rapid discovery of 2D ferromagnetic semiconductors/half-metals/metals [J]. Advanced Materials， 2020， 32（29）：2002658.

[20]JIANG P， WANG C， CHEN D C， et al. Stacking tunable interlayer magnetism in bilayer CrI3 [J]. Physical Review B， 2019， 99（14）：144401.

[21]WANG C， ZHOU X Y， ZHOU L W， et al. Bethe-Slater-curve-like behavior and interlayer spin-exchange coupling mechanisms in two- dimensional magnetic bilayers [J]. Physical Review B， 2020， 102（2）：020402.

[22]MAY A F， OVCHINNIKOV D， ZHENG Q， et al. Ferromagnetism near room temperature in the cleavable van der Waals crystal Fe5GeTe2 [J]. ACS Nano， 2019， 13（4）：4436-4442.

[23]KRESSE G， FURTHMULLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set [J]. Physical Review B， 1996（54）：11169-11186.

[24]PERDEW J P， BURKE K， ERNZERHOF M. Generalized gradient approximation made simple [J]. Physical Review Letters， 1997，78（7）：1396-1396.

[25] DUDAREV S L， BOTTON G A， SAVRASOV S Y， et al. Electron-energy-loss spectra and the structural stability of nickel oxide： AnLSDA + U study [J]. Physical Review B， 1998， 57（3）：1505-1509.

[26] ANISIMOV V V， ZAANEN J， ANDERSEN O K. Band theory and mott insulators： Hubbard  U instead of stoner I [J]. PhysicalReview B， 1991， 44（3）：943-954.

[27] LI X， YANG J. CrXTe3（X = Si， Ge） nanosheets： Two dimensional intrinsic ferromagnetic semiconductors [J]. Journal of MaterialsChemistry C， 2014， 2（34）：7071-7076.

[28] DONG L， KUMAR H， ANASORI B， et al. Rational design of two-dimensional metallic and semiconducting spintronic materials basedon ordered double-transition-metal MXenes [J]. Journal of Physical Chemistry Letters， 2017， 8（2）：422-428.

[29] MONKHORST H J， PACK J D. Special points for brillouin-zone integrations [J]. Physical Review B， 1976， 13（12）：5188-5192.

[30] TOGO A， TANAKA I. First principles phonon calculations in materials science [J]. Scripta Materialia， 2015， 108：1-5.

[31] BARONI S， GIRONCOLI S D， CORSO A D， et al. Phonons and related properties of extended systems from density functionalperturbation theory [J]. Review of Modern Physics， 2001（73）：515-562.

[32] GOODENOUGH J B. Theory of the role of covalence in the perovskite-type manganites [La， M（II）]MnO3 [J]. Physical Review， 1955，100（2）：564-573.

[33] ANDERSON P W. New approach to the theory of superexchange interactions [J]. Physical Review， 1959， 115（1）：2-13.

（責任编辑：李艺）