基于综合效益的城市轨道交通票价模型研究

李 英

（浙江育英职业技术学院 民航交通分院，浙江 杭州 310018）

近十年来，在借鉴国外轨道交通定价策略的基础上，结合国内轨道交通运营的实际情况及国情，我国部分城市对轨道交通票价进行了初步改革。《关于改革完善高铁动车组旅客票价政策的通知》（发改价格〔2015〕3070 号）针对高铁动车组的票制票价的改革完善提出了要求；北京地铁结合各方面的考虑，于2014 年底对实施多年的两元单一票制进行改革，调整为按乘车距离计价的计程票制[1]；另外，深圳、武汉、南京等城市地铁票价水平也进行了调整。城市轨道交通票价问题，是交通领域专家关注的重要经济课题，已取得了一些研究成果，为制定和完善城市轨道交通票价提供了重要的理论参考[1-4]。但鲜有研究从城市轨道交通带来的综合效益的角度，探讨轨道交通定价方案。为此，笔者基于综合效益，研究城市轨道交通票价的制定和优化问题，这为轨道交通票价调整提供一种新方法，具有现实意义。

1 模型构建

1.1 假设条件

为科学分析问题，本模型构建基于以下假设条件。

假设1：城市轨道交通运营企业的内部效益仅考虑主要收益（即票务收益），其他非票务收益（如广告收益、租赁收益等）暂不进行考虑；

假设2：给城市发展带来的效益的计算过程中，涉及到的相关参数取一年的量值来计算。

1.2 企业效益

根据经济学非完全竞争市场理论，轨道交通企业收益可表示为式（1）。

式（1）中，P 为城市轨道交通平均票价(元/人次)；Q 为票价P 时的年客流量(万人次)；C 为城市轨道交通运营成本（万元）；Fr 为城市轨道交通企业收益（万元）；ε 为客流量票价弹性系数，ε＜0，θ 为成本弹性指数；α、β 为对应参数。

1.3 乘客效益

乘客效益可以通过乘客对城市轨道交通运输服务各方面指标的评价及其在乘客心中的权重系数综合评定。主要影响因素有：货币成本、舒适性、方便性、安全性和准时性。乘客效益可表示为式（2）。

式（2）中，u 为单位地铁乘客出行效益；Fu为乘客效益总量。评价指标为安全性（m1）、舒适性（m1）、方便性（m2）、准时性（m3）、货币成本（票价P）及其对应值σ1、σ2、σ3、σ4、σ5。将通过问卷调查根据乘客对地铁的票价、安全、舒适性、方便性及准时性的评价来获得。

1.4 社会效益

对比城市轨道交通与城市道路公共交通，城市轨道交通产生的外部效益表示为式（3）。

式（3）中：Fe 为城市轨道交通产生的社会效益总量；E1为轨道交通在节约时间方面产生的外部效益；E2为城市轨道交通在减少城市环境污染方面产生的外部效益；E3为城市轨道交通在减少交通事故损失方面产生的外部效益；E4为城市轨道交通在房产升值方面产生的外部效益（由于轨道交通车站距离房产所在地的空间距离是显著影响因素。所以，票价这一因素对地产升值的影响可以忽略[5]。

E1可以表示为式（4）。

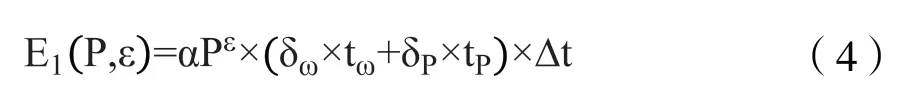
式（4）中，δω为平均每日工作客流的比例；tw为工作客流单位时间价值（元/h）；δp为平均每日休闲客流的比例；tp为休闲客流单位时间价值（元/h）；△t 为选择乘坐城市轨道交通较选择地面公交节省出行时间的平均值（h）。

E2可表示为式（5）。

E3可表示为式（6）。

式（6）中，gb为路面公交事故的年平均发生率（次/万人·km）；gr为城市轨道交通事故的年平均发生率（次/万人·km）；1b为路面公交事故的年平均损失额（元/次）；1r为城市轨道交通事故的年平均损失额（元/次）。

1.5 约束条件

1.5.1 经济水平约束

世界银行的统计数据表明，发展中国家的居民用于交通方面的费用支出占其可支配收入的比例一般为5%-10%。因此从居民用于城市轨道交通方面票价支出的经济承受力方面，城市轨道交通票价受约束的条件可表示为：5%≤MC/Mr≤10%。因此，MC=P×2×30。MC为轨道交通月出行费用；Mr 为当地居民月平均可支配收入。

1.5.2 线网客流约束

票价变化影响客流量，客流量上限为城市轨道交通系统最大承受客流量Qmax，即：αPε≤Qmax。

1.6 票价模型与求解

综上，城市轨道交通票价制定的目标函数，见式（7），应用多目标函数求解方法求解[6]。

2 算例描述与分析

2.1 算例描述

以某城市为例，本文选取2013-2020 年的客流量、成本和票价数据，运用MATLAB 最小二乘法作回归分析，对应的估计参数和拟合方程结果见表1。

表1 客流、平均票价、运营成本函数关系拟合结果

因此，该城市轨道客流量与票价之间的关系为：Q=314771×P-2.4199；运营成本与客流量的关系表示为：C=10897×Q0.1882。根据式（1）:该城市轨道交通运营企业的收益为式（8）。

影响乘客选择出行方式选择的主要因素有安全性、舒适性、便捷性、准时性、货币成本。本次调查发放问卷200 分，回收167 份，有效问卷150 份。通过乘客对于这五个影响因素按重要性进行打分，从而得到各个影响因素的权重值，得到的调查和分析结果见表2。

表2 目标函数中各评价指标值及权重系数的确定

因此，根据式（2），代入参数取值，乘客效益表示为式（9）。

研究结果表明，上班、上学乘客群体的平均出行时间价值tω为10.39 元/h，探亲访友、休闲娱乐乘客群体的出行平均时间价值tP为8.30 元/h[7]。调查数据统计表明，该城市乘客出行平均节约时间0.58h，其中通勤客流的比例为29%，休闲客流的比例71%。

参考我国其他地区不同交通方式废气的排放密度，即每人·km 废气排放量的数据可知，地铁人·km 的排放量为0g，私人汽车人·km 废气的排放量为172g，公共汽车人次排放量为51g；废气排放价格为0.1863 元／kg[8]。而由于该城市路面公交采用的是绿色环保的电动公交，因此，与路面公交比较，在环境保护方面，地铁的外部效益为0。根据调查，目前该城市地铁乘客乘坐轨道交通出行的平均出行距离在10-11km 之间。

根据城市道路交通事故损失率调查数据，平均每万人·km 发生事故导致的直接损失达到0.004万元[9]。而该城市地铁自开通运营以来实现了零运营事故。所以，对于该城市地铁，在安全性上产生的外部效益（城市交通事故损失减少值）可以表示为式（10）。

根据官方数据，该城市月平均收入Mr 取值4349 元。从居民交通消费支出结构和水平看，最近几年交通消费支出占人均可支配收入的比例达10%。因此地铁票价受居民经济承受力的约束可用以下式子表示：MC/Mr≤10%。

2.2 算例结果分析

根据式（7）和2.1 节参数说明，票价计算公式为式（11）。

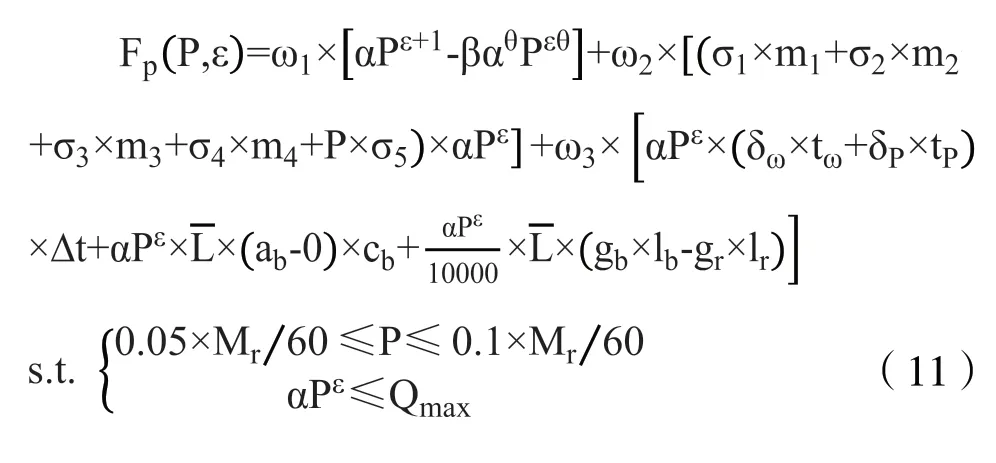
本论文邀请了该领域的相关专家，采用德尔菲法，确定了在客流培育期阶段取值，ω1=0.1，ω2=0.8，ω3=0.1。随着外界环境、轨道交通的情况等因素的改变，在充分调研的基础上，可以调整各目标的权重，以调整为与当时阶段相符合的最优票价。将相关参数代入票价模型，如式（12）。

考虑到地铁客流的不均衡性，在目前的运营管理现状下，该城市轨道交通线路可运输的年最大客流量，即Qmax可达到30000 万人次。见式（13），综合效益函数在0 ≤P ≤7.3 范围内为递减函数，采用无穷递降逐步逼近法，求出当前运营阶段，综合效益最大的平均票价为2.6 元。

根据调研，目前该城市地铁平均出行距离在10-11km 之间，按照目前的票价水平和阶梯费率，平均出行距离的车票花费在3-4 元，与实际票务数据相符。考虑到计费方式的相对稳定性，因此建议该地铁在依然采用计程票制和原有起步价、封顶价基础上，增加起步价1km 的乘车距离。建议方案如表3。

表3 地铁票价建议方案

3 结束语

本文创新研究视角，考虑企业、乘客、社会等方面效益因素，研究票价问题，构建一种使得城市轨道交通发挥最大效益的多目标票价量化模型。该定价模型在效益最大化方面具有很大的优势，将为我国处于不同运营阶段的城市轨道交通票价的制定和调整提供新的思路和方法。本研究的不足之处表现为仅考虑平均票价水平，没有对计程票制结构和费率进行深入研究，这将成为笔者进一步拓展研究的方向和内容。