结合共享近邻和共享逆近邻的密度峰聚类

周欢欢，张 征，张 琦

(西华师范大学 数学与信息学院，四川 南充 637009)

聚类分析是数据挖掘的重要研究领域之一，是一种无需先验信息的无监督学习方法[1]。聚类分析的主要目的是：根据某种相似度度量关系分析未标记数据点之间的联系，从而揭示数据内在的属性[2-4]，将彼此相似的样本点归为同一个簇，同时使不同类簇的样本点相似度尽可能小。学者基于不同理论提出了许多不同的聚类算法，这些聚类方法可分为基于划分、网格、模型、层次和密度的聚类算法[5]。

Rodriguez和Laio于2014年提出的密度峰聚类算法[6](Clustering by fast search and find of Density Peaks，DPC)能处理具有任意形状的数据集。由于该算法具有原理简单、无需迭代并且通过决策图能准确找到聚类中心等优点，自被提出以来便引起了广泛关注，在短时间内就被应用到计算机视觉[7]、医学[8]、图像识别[9]、生物学[10]等各个领域。但是DPC算法也存在缺陷：(1)基于欧氏距离和截断距离定义样本的相似度和局部密度，导致对高维数据集和分布不均数据集的聚类结果不理想；(2)分配策略容错能力差，样本点分配错误会引起链式反应进而导致一连串的样本点分配错误；(3)全局参数截断距离dc难以确定。

针对DPC算法存在的不足，学者提出了一些相应的改进算法。Du等[11]提出了基于k近邻的KNN-DPC算法，该算法引入了k近邻的概念和主成分分析法，提供了一种新的计算局部密度的方法，能反映数据的局部结构；Guo等[12]提出了基于逆近邻的NDPC算法，将DPC算法的局部密度重新定义为每个样本点的逆近邻数，能较好地处理密度不均衡数据；鲍舒婷等[13]提出了基于共享近邻相似度的DPCSNNS算法，克服了DPC算法对截断距离敏感的问题；Xie等[14]提出了FKNN-DPC算法，该算法引入了k近邻的新局部密度和基于模糊准则的分配策略；Liu等[15]提出了基于共享近邻的SNN-DPC算法，依据共享近邻的思想重新定义了相似度、局部密度和距离度量，并提出了两步分配非聚类中心的方法，该算法不仅能处理高维复杂数据集，还能避免样本点被错误分配时产生的链式反应。

目前，大部分DPC改进算法通过k近邻、逆近邻或共享近邻来构造样本之间的相似度，忽略了两个点之间的相似度与这两个点的共享近邻和共享逆近邻都有关。鉴于此，为了更好地解决DPC算法的不足，本文提出了结合共享近邻和共享逆近邻的密度峰聚类算法，同时考虑到了样本点之间的共享近邻和共享逆近邻。该算法利用共享近邻和共享逆近邻构造新的相似度，并通过该相似度提出了一种新的局部密度度量方法。同时，提出了基于近邻和逆近邻的分配策略，以从众的思想分配样本点，避免样本点被分配错误时出现的链式反应。

1 DPC算法

DPC算法的聚类中心主要具备两个基本的设定：(1)聚类中心被密度较低的近邻点包围；(2)聚类中心之间的距离相对较远，即聚类中心与具有较高局部密度的点距离相对较大。根据假设可知，聚类中心拥有较大的局部密度和距其他聚类中心相对较远。要确定数据集的聚类中心，需要计算每个样本点的局部密度ρ和距离δ。DPC算法采用两种方法计算样本点的局部密度：

当数据规模比较大时，采用截断核计算局部密度ρi，计算公式为：

(1)

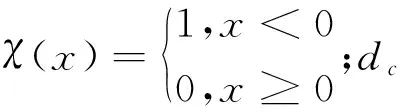
(2)

其中，N是样本点的维数。

当规模比较小时，采用指数核[16]计算局部密度ρi，计算公式如下：

(3)

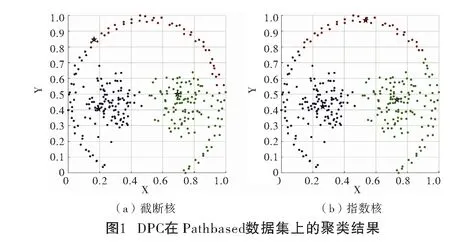
式(1)和式(3)中的截断距离都需要人为设定，并且截断距离的微小变化会引起聚类结果的剧烈波动。文献[6]认为截断距离的设定通常要满足样本平均近邻的数量为数据集的1%～2%。

样本点的距离计算公式如下：

(4)

DPC算法以每个样本点的局部密度ρ和距离δ为依据，文献[6]提出用下式来计算每个样本点的决策值，进而构造决策图。根据决策图选取较大的决策值γi为聚类中心，即聚类中心拥有较大的ρi和δi值。

γi=ρiδi。

(5)

DPC算法根据决策图选出聚类中心之后，将剩下的样本点分配到距其最近且具有更大局部密度的点所属的簇。

2 结合共享近邻和共享逆近邻的密度峰聚类

2.1 相关定义

定义1(k近邻集)样本点i与其他样本点的欧式距离最近k个点的集合，称为样本点i的k近邻集KNN(i)，数学表达如下：

KNN(i)={j∈X|dij≤diik}，

(6)

其中，dij表示样本点i和j的欧式距离，ik是样本点i到其他点欧式距离升序排序后位于第k个位置的样本点，X是数据集。

定义2(逆近邻集[17])如果样本点i在其他样本点的k近邻集中，则称这些样本点为点i的逆近邻集RNN(i)，数学表达如下：

RNN(i)={j∈X|i∈KNN(j)}。

(7)

定义3(共享k近邻集[18])样本点i和j的共享k近邻集SNN(i,j)定义如下：

SNN(i,j)=KNN(i)∩KNN(j)。

(8)

定义4(共享逆近邻集)样本点i和j的共享逆近邻集SRNN(i,j)定义如下：

SRNN(i,j)=RNN(i)∩RNN(j)。

(9)

定义5(距最近较大密度点的距离[15])样本点i的局部距离δi值公式如下：

(10)

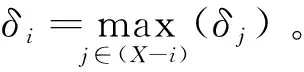
2.2 基于共享近邻和共享逆近邻改进的局部密度

由于DPC算法以欧氏距离来度量样本点之间的相似度，而欧氏距离只考虑样本点之间的局部一致性，导致DPC算法处理样本点分布不均和高维复杂数据集的聚类效果不理想。因此，本文借助共享近邻和共享逆近邻构造了相似度，包含了两个点之间的k近邻和逆近邻的信息，k近邻能反映数据的局部特征，逆近邻从全局的视角获得样本点的密度信息。

定义6(相似度)对于数据集X中样本点i和j，它们之间基于共享近邻和共享逆近邻的相似度定义为：

(11)

其中，NN(i,j)=SNN(i,j)∪SRNN(i,j)；dip表示样本点i和p的欧式距离；| |表示集合的元素数量。

高月等[19]证明了逆近邻能更好地反映样本的密度信息，所以本文提出了以逆近邻为主的局部密度，样本点的局部密度是每个样本点与其逆近点的相似度之和除以该点的逆近邻集的元素数量。

定义7(局部密度)∀i∈X，样本点i的逆近邻集中的所有样本点与该点的相似度之和除以该点逆近邻的数量，则为点i的局部密度ρi。局部密度ρi公式如下：

(12)

2.3 分配策略

算法1：样本点分配算法

Step1:初始化队列Q，将所有的聚类中心点放入队列Q中；

Step2:取队列Q头部点为xi，获得xi的k个近邻点，其集合为Ki；

Step2-1:取未分配的点x′，其中x′∈Ki；

Step2-3:重复Step2-1至Step2-2两个步骤，直至集合Ki中k个近邻点处理完成；

Step2-4:将k个近邻点处理完后，从队列Q中删除头部点；

Step3:跳转Step2反复循环，直至队列Q为空；

Step4:找到所有未分配的样本点pi，设未分配的点有b个，那么i=1，2，…，b；

Step5:构造分配矩阵A，初始值为0，其中分配矩阵行数等于b，列数等于簇数m；

Step6:对每个未分配的样本点pi，i=1,2,…,b，找到pi的所有k个近邻点qij，j=1，2，…，k。如果点qij已经被分配给某个簇c，1≤c≤m，则Aic=Aic+1；

Step7:求出分配矩阵A中所有行里的最大值max(max>0)，用最大值所在的簇来表示该行未分配点簇。

Step8:循环Step4—Step7，直至所有样本点分配完。

2.4 完整算法

至此，给出结合共享近邻和共享逆近邻的密度峰聚类的完整算法如下：

算法2：结合共享近邻和共享逆近邻的密度峰聚类算法

Step1:输入数据集X，簇数m；

Step2:根据式(6)和(7)计算每个样本点的k近邻集和逆近邻集；

Step3:根据式(11)计算每个样本点与其他点的相似度Sim；

Step4:根据式(12)计算每个样本点的局部密度ρi；

Step5:根据式(10)计算每个样本点对应的距离δi；

Step6:根据式(5)计算每个样本点的决策值γi；

Step7:对Step6得到的决策值排降序，并且自动选取排序后列表中前m个样本点作为聚类中心；

Step8:通过样本点分配算法将剩下的样本点分配到相应的簇中；

Step9:输出聚类结果。

3 实验结果及分析

为了验证算法的性能，本文在人工数据集和UCI真实数据集上进行测试。采用AMI[20]、ARI[20]和FMI[21]为评价指标，并与SNNDPC[15]、传统DPC[6]、FKNN-DPC[14]、DBSCAN[22]、OPTICS[23]、AP[24]和K-Means[25]算法进行比较。

在进行实验之前，采用最大最小归一化方法对数据集进行预处理，以消除数据的缺失和维数差异对聚类结果的影响。最大最小归一化方法如下式所示：

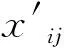
3.1 人工数据集实验结果

选取7个人工数据集进行仿真实验，数据集的详细信息如表1所示，所选数据集具有不同的样本个数和簇数。图2～图8是人工数据集的原始聚类图和本文算法获得的聚类效果图对比，其中具有不同颜色的点被分配给不同的簇，聚类中心以星号表示。Aggregation数据集包含7个形状规模不同的多密度团状簇；Flame、S2和D31数据集具有簇与簇之间距离较近的特点；R15数据集包含15个形状不一的簇；Spiral是螺旋形数据集；Pathbased数据集的特点是数据分布不均。从图2～图8可以看出，本文聚类算法借助共享近邻和共享逆近邻的概念，能准确找到数据集每个簇的聚类中心；基于近邻和逆近邻的分配策略能正确分配簇边缘区域样本点。本文算法避免了DPC算法中截断距离难以选取的问题，克服了DPC算法人工选择局部密度计算方法的缺陷，以及能处理分布不均的数据集。

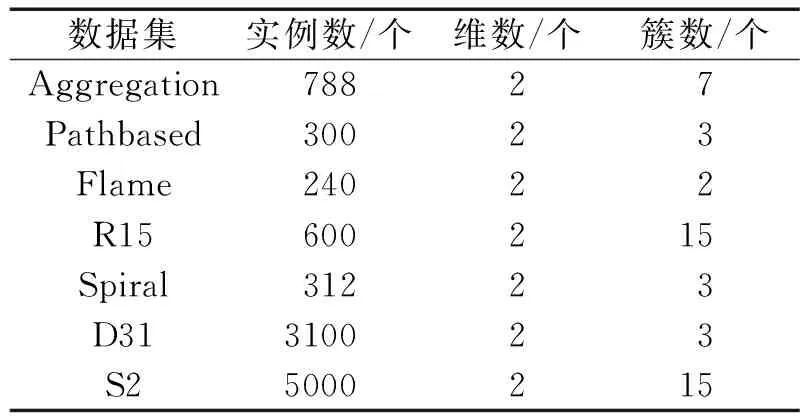
表1 人工数据集

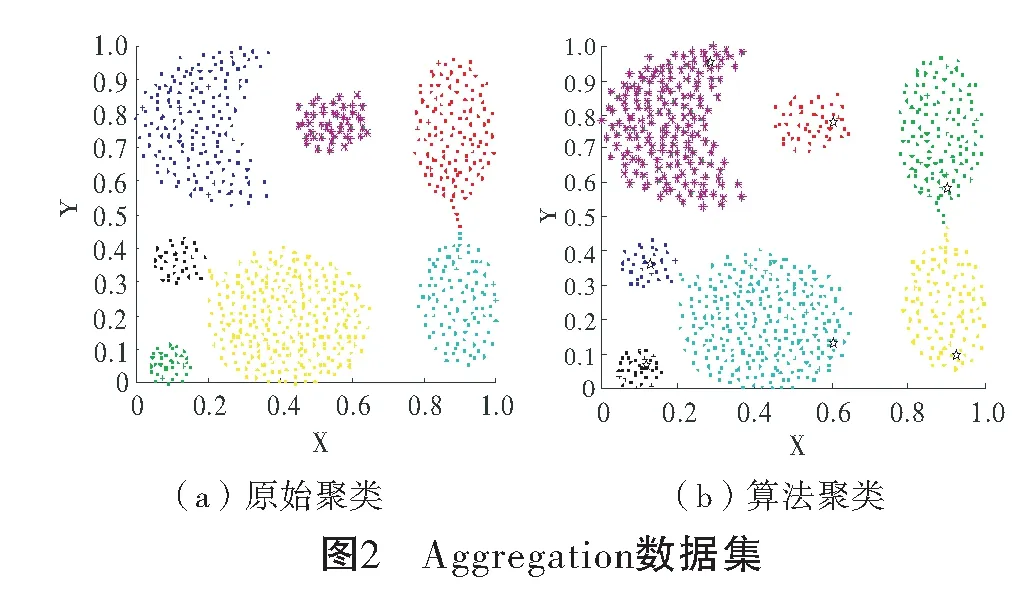
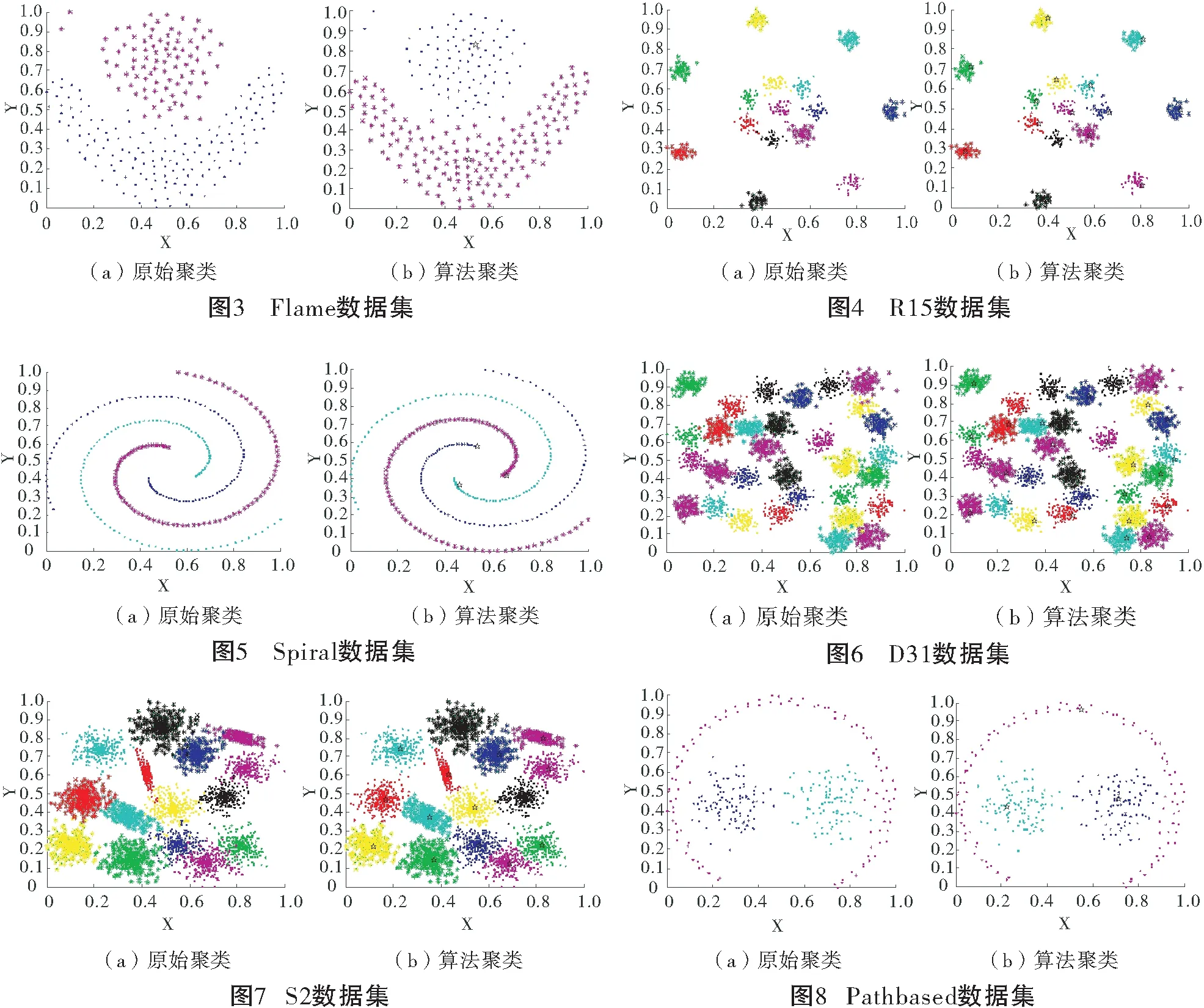
表2是本文算法与其他7种算法在7个人工数据集上的评价指标结果，表中加粗的值表示最好的聚类结果。由实验结果知，除了Aggregation和Flame数据集，在其他数据集中本文算法的AMI、ARI和FMI值均优于其他算法，尤其在Pathbased数据集上，本文算法得到的AMI、ARI和FMI值分别比DPC算法高41.44%、48.8%和30.67%。在Aggregation数据集上，比DPC算法的AMI、ARI和FMI值分别低0.44%、0.22%和0.17%；在Flame数据集上，比DPC算法的AMI、ARI和FMI值分别低7.33%、3.34%和1.55%。

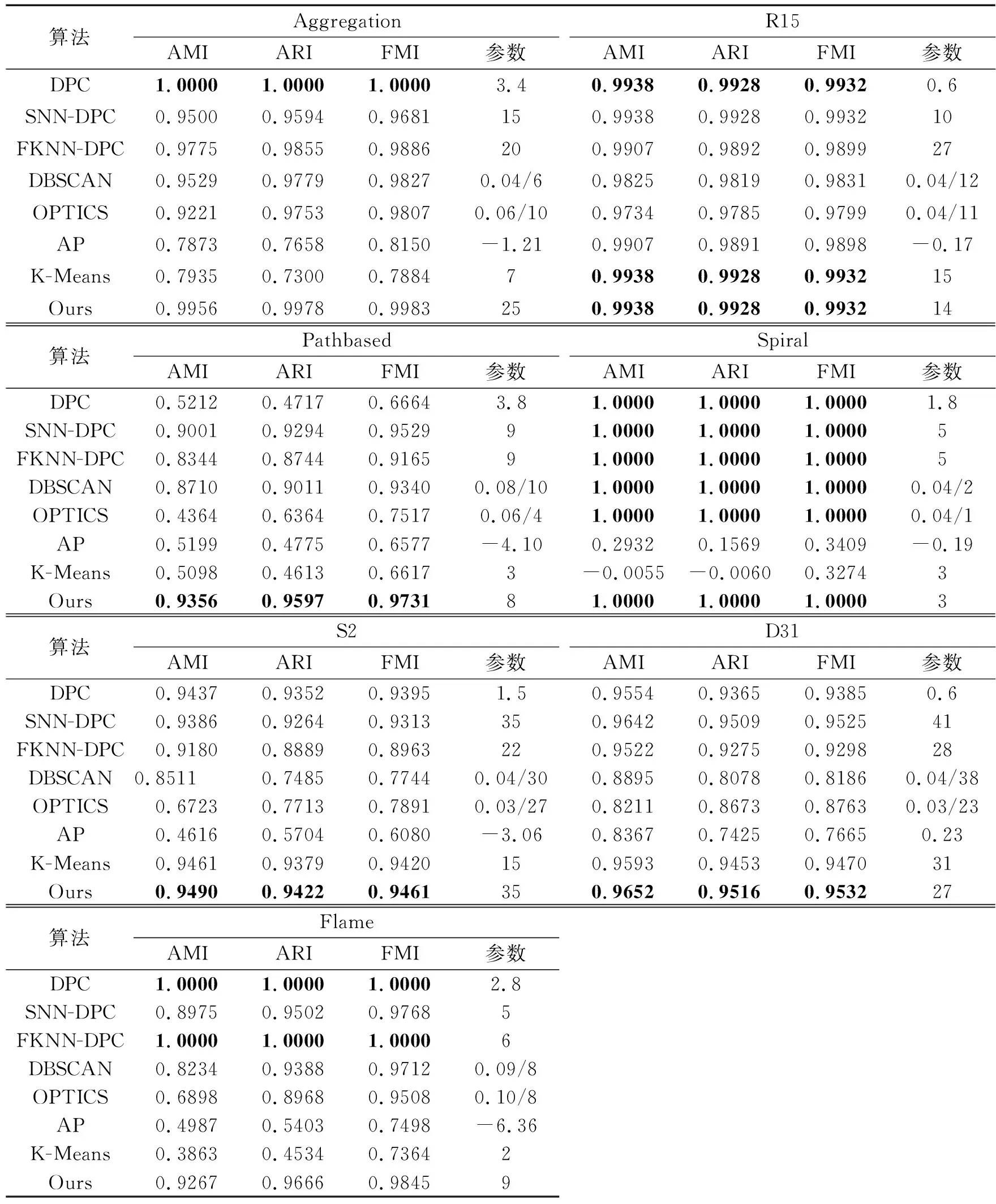
表2 人工数据集聚类结果

3.2 UCI数据集实验结果

选取4个数据分布不一样的UCI数据集进行测试，数据集的详细信息如表3所示。各算法在UCI数据集的聚类结果如表4所示。Wine数据集包含3个分布不均的簇，本文算法得到的AMI、ARI和FMI值分别比DPC算法高18.49%、24.25%和16.00%；Iris数据集包含3个规模一样的簇，本文算法得到的AMI、ARI和FMI值分别比DPC算法高5.27%、3.65%和2.46%,与SNN-DPC算法聚类结果一样；Seed数据集包含3个样本点数量相同的簇，本文算法得到的AMI、ARI和FMI值分别比DPC算法高6.30%、6.56%和5.96%；Blance Scale数据集是平衡比例尺数数据集，本文算法得到的AMI、ARI和FMI值分别比DPC算法高32.98%、32.37%和20.55%。同时本文算法的AMI、ARI和FMI值均优于其他算法。

表3 UCI数据集

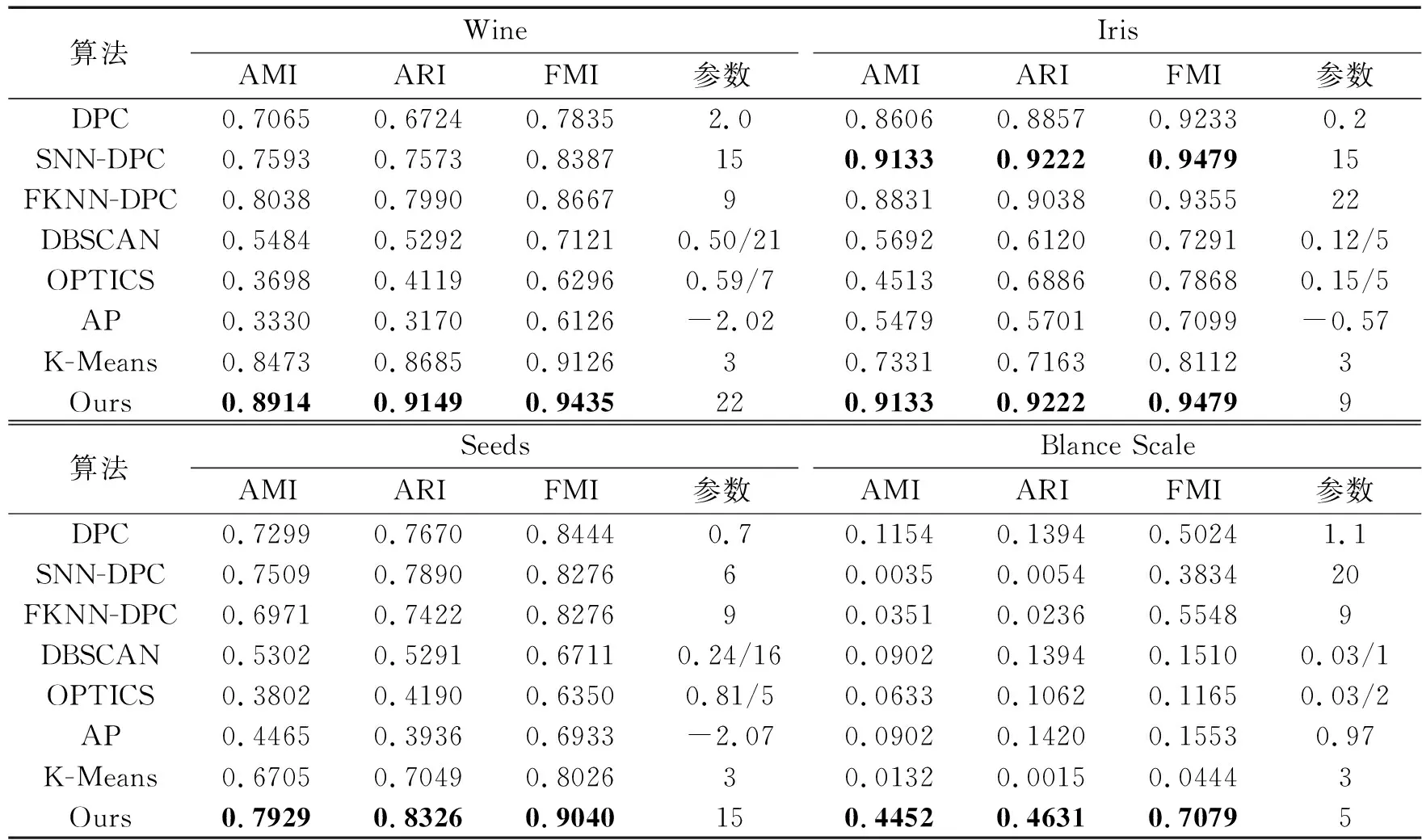
表4 UCI数据集聚类结果

4 结 语

为了解决DPC算法的局部密度定义过于简单、全局参数截断距离难以确定以及聚类分配策略容错能力差等问题，提出了一种结合共享近邻和共享逆近邻的密度峰聚类算法。该算法借助共享近邻和共享逆近邻定义了新的相似度与局部密度，能更准确反应数据的局部特征和内在联系，找到准确的聚类中心，避免了参数截断距离的选择。同时，提出了一种新的分配策略，能有效避免样本点被错误分配时导致进一步的错误。实验结果表明，与其他算法相比，本文算法可以处理更多类型的数据集，整体上具有理想的聚类效果。