斜入射非线性电离层Langmuir 扰动的电磁波传播特性*

杨利霞 刘超 李清亮 闫玉波

1) (安徽大学电子信息工程学院,合肥 230031)

2) (安徽大学,信息材料与智能感知安徽省实验室,合肥 230031)

3) (中国电波传播研究所,电波环境特性及模化技术重点实验室,青岛 266107)

1 引言

电离层作为一种时变的非均匀磁化等离子体,会与入射到其中的电磁波发生复杂的相互作用[1].一般地,利用高功率寻常波(O 波)对电离层进行加热实验,由于参量衰变不稳定性,泵波可在反射高度附近激发出电子Langmuir 波和离子声波[2],同时波粒相互作用导致O 波转换为Z 波并向电离层更高区域传播,进一步形成Langmuir 扰动[3],Langmuir 扰动的形成可引起非相干散射雷达背向散射功率增强,即离子线与等离子体线的增强现象.

电离层加热是近年来电波传播领域的热点问题,电离层局部加热性导致等离子体的非线性变化[4],可以极大地改变局部地区的电磁波传播特性,具有重要的研究价值和军事研究意义.而Langmuir扰动是电离层加热效应的重要研究方向之一[5,6],国外研究人员做了大量的Zakharov 模拟实验来研究电离层中强扰动和弱扰动的特性,并将得到的能量谱与观察到的受激电磁辐射以及雷达观测结果进行比较[7,8].Zakharov 模型对时间尺度进行了划分,得到高频电磁场的复数包络和等离子体低频响应的方程[9].Mjølhus 等[10]建立了一个两级模型来表示Langmuir 扰动和电磁波之间的耦合,对Langmuir 波使用Zakharov 模型,对电磁波使用格林函数法.Eliasson 等[11,12]进行了一系列的研究,对电离层Langmuir 扰动建立了一维(1D)广义Zakharov 数值模型.目前国内对Langmuir 扰动本身的研究尚处于起步阶段,如武汉大学的刘默然等[13]、何昉等[14]以及江苏大学的朱婷[15]都对电离层垂直加热下Langmuir 的扰动进行了数值模拟研究.

对于斜入射[16]电离层加热下Langmuir 的扰动目前国内研究较少,为此,本文基于广义Zakharov模型,通过将二维(2D)麦克斯韦方程等价地转换为一维麦克斯韦方程[17,18],避免了用传统的二维时域有限差分方法分析该散射问题,这样将节省大量内存,极大地提高计算效率,有效降低编程的复杂程度.同时,深入细致地研究计算背景为等离子体的斜入射问题,从而进一步研究基于电离层非线性等离子体扰动的电磁波传播特性的全尺度时域计算方法,并基于上述方法分析电离层扰动的电磁场分布和传播特性.

2 斜入射非线性等离子体下Langmuir扰动分析

2.1 斜入射非磁化等离子体的迭代式推导

TEz斜入射非磁化等离子体的示意图如图1所示,其中介质区间1 和3 表示真空,介质区间2表示电离层等离子体.这里选取电磁波的波数k与z轴夹角为θ,T Ez波在区间1 中以θ角度斜入射到等离子体区域中.

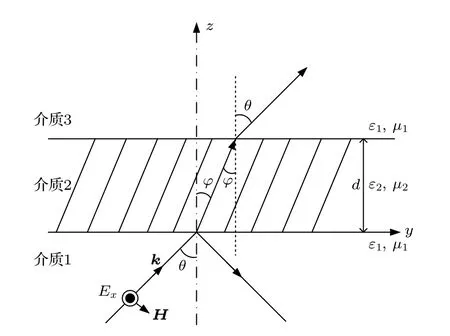
图1 TEz 波斜入射电离层等离子体的传播模型Fig.1.Propagation model of TEz wave obliquely incident ionospheric plasma.

由图1 可知,在斜入射情况下,电磁波在电离层中的传播过程是一个二维问题.从宏观角度来看,将麦克斯韦旋度方程在直角坐标系下展开,可得 T Ez波在区间1 的时域麦克斯韦方程:

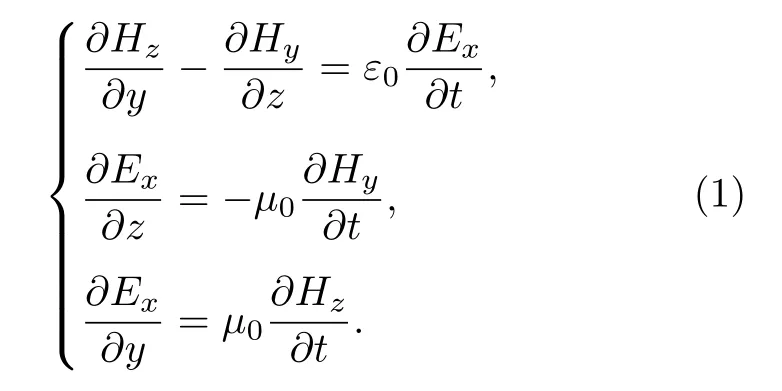
根据文献[19]中的推导方法,最终(1)式可化为时域里等价的一维形式:

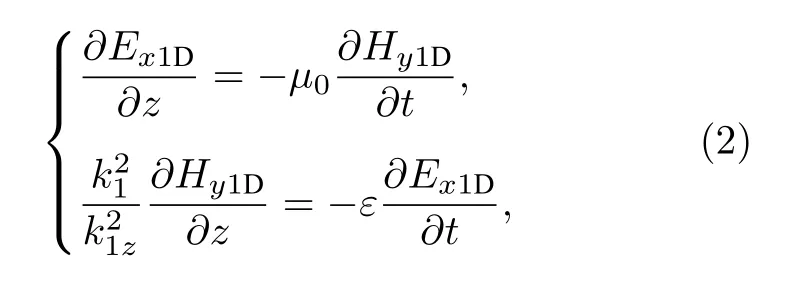
式中k1为区间1 (真空)中的电磁波波数,k1z为k1在z轴方向上的投影,即k1z=k1cosθ.

同理,在区间2 (等离子体)中,一维斜入射情况下电磁波同样满足(2)式形式的一维解,并转换到频域:

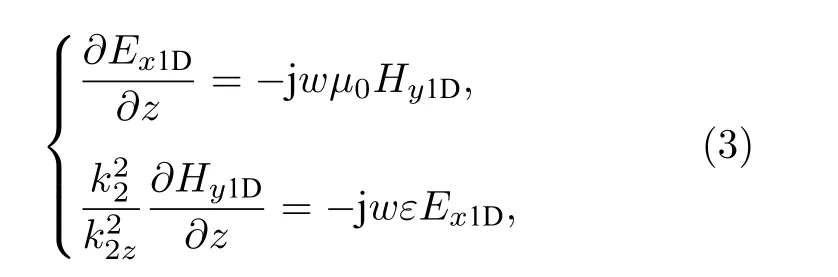
式中k2为区间2 (电离层等离子体)中的电磁波波数,k2z为k2在z轴方向上的投影,即k2z=k2cosϕ.

为了解决区间1,3 与区间2 的电磁波传播过程中遇到的相位及边界问题,由边界条件和相位匹配原理知将其代入(3)式得

对方程(4)中的第2 式进行整理,可得

式中磁化等离子体的相对介电常数为矩阵形式,可写为

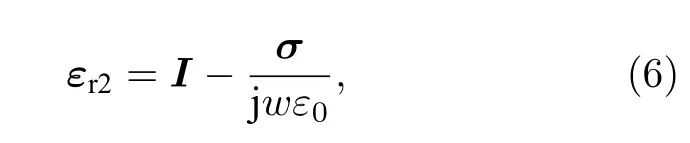
其中σ表示电导率,将(6)式代入(5)式并通过逆傅里叶变换到时域,可得

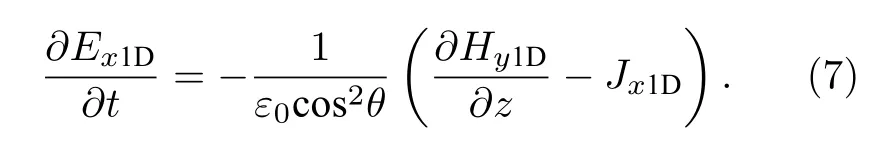
在等离子体介质中电流密度为

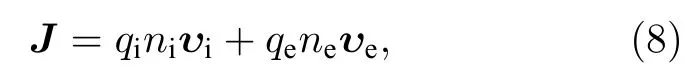
其中,下标“ i ”表示离子,下标“e”表示电子.

由于离子的质量远大于电子的质量,离子成份的流体速度远小于电子成份,离子可以被视为是静止的.忽略离子部分后将(8)式代入(7)式,最后联立(4)式的第一个式子并进行逆傅里叶变换,可得

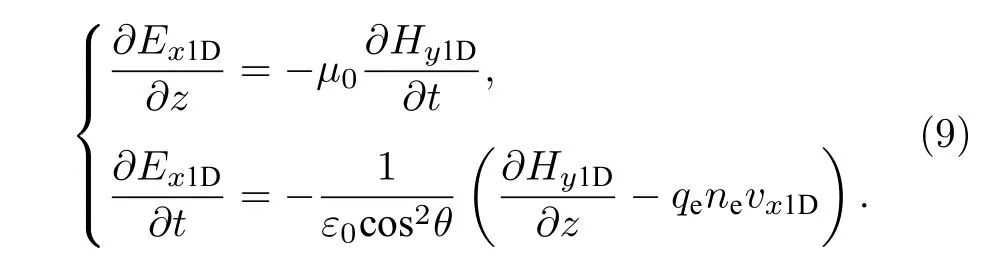
同理推导Ey1D,Hx1D具有相似的形式:

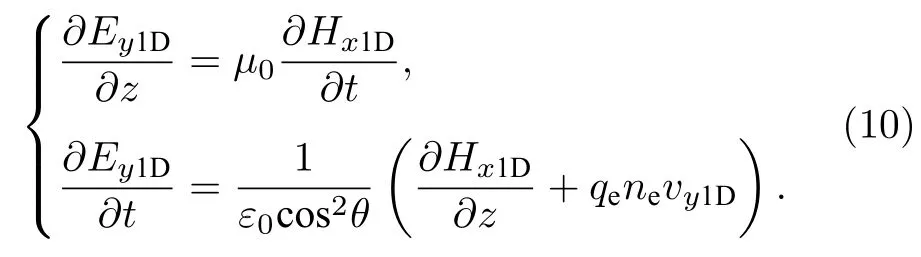
电离层等离子体可被看成是由电子流体和离子流体组成的导电的连续介质,因此描述等离子体运动采用流体力学方程.在双流体力学描述中,带电粒子的数密度和流体速度分别满足连续性方程和动量方程:

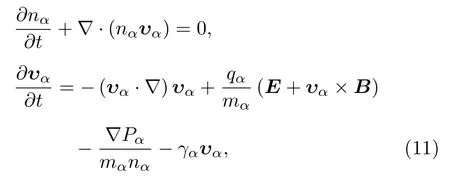
式中nα为粒子数密度,υα为粒子的流体速度,qα表示粒子电荷;磁感应强度B=B0+B1,其中B0是地磁场,B1是波磁场;mα是粒子质量;Pα是压强;γα是与粒子间碰撞等因素有关的阻尼算子.

将(11)式中的电子数密度连续性方程,经过高斯定理推导出如下形式:

对于高频波,(11)式中的电子动量方程变为

(9)式、(10)式、(12)式和(13)式构成了高频电磁波斜入射电离层等离子体的非线性耦合方程组,也是此研究的理论基础.

时域有限差分方法可以直接求出Maxwell 方程组显式下的离散形式,(9)式和(10)式进行离散后得到磁场强度的迭代方程为

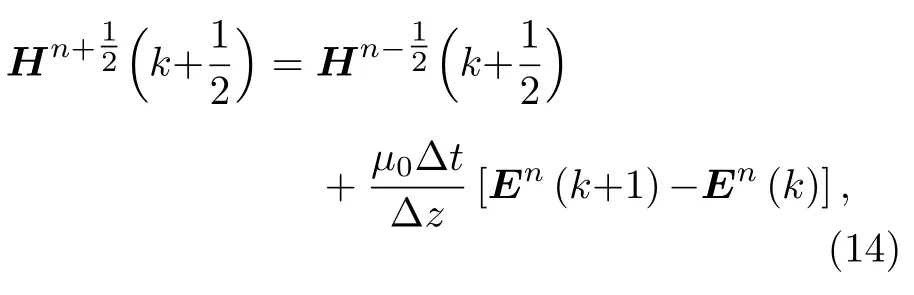
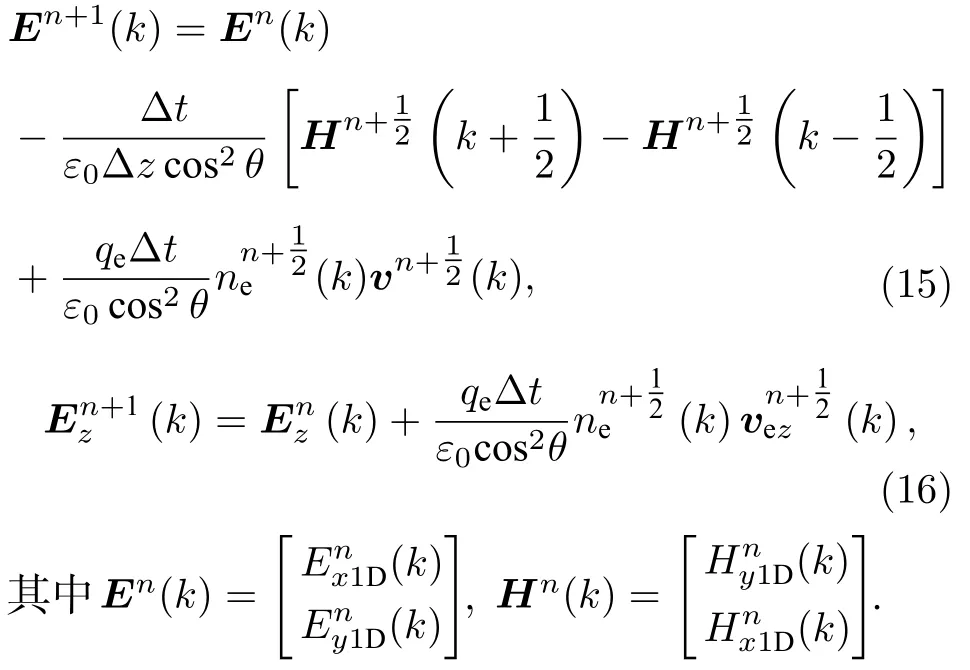
从迭代式(14)—(16)可以看出,电场的垂直分量E⊥与磁场的垂直分量以及等离子体密度、流体速度密切相关,而电场的平行分量Ez仅与其本身、电子的数密度和z方向的流体速度有关.

对(12)式关于空间的一阶偏导数选取后向差分近似,得到电子密度的离散迭代方程为

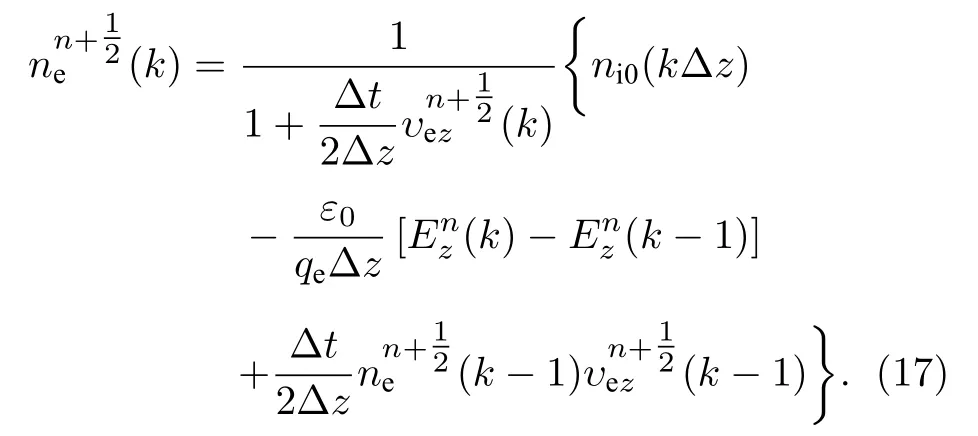
对(13)式等号右侧的第一项作近似处理,再通过矩阵求解得到电子流体速度的离散迭代方程为

电磁波在电离层中斜入射传播过程的时域数值完整迭代步骤如图2 所示.

图2 FDTD 电磁场时域的逐步迭代流程图Fig.2.Step by step iterative flow chart of FDTD electromagnetic field in time domain.

2.2 数值算法的稳定性条件

1)时间离散间隔的稳定性要求

在使用FDTD 算法对电磁波在电离层中的传播进行数值仿真时,需要考虑等离子体与电磁波相互作用的影响.等离子体中空间和时间离散间隔之间应当满足的充分条件[20]为

其中wpe为等离子体特征频率.(19)式表明一维情况下,时间间隔必须等于或小于波以光速通过Yee元胞所需的时间.

2)数值色散对空间离散间隔的稳定性要求

有限差分代替波动方程的二阶导数过程中,离散处理将会导致波的色散,此时需要对空间离散间隔做出要求来降低色散,一维情况下要求

式中λ对应介质中的最小波长.

本次数值模拟选取λ=60 m ,Δz=1 m,并使Δt满足Courant 条件,本文在50—400 km 全范围内以1 m 步进计算.

2.3 数值模型

本文建立的电磁波斜入射电离层的数学模型如图3.数值模型采取的实际参数来自EISCAT 在挪威的电离层加热实验[21,22],考虑到参量不稳定性发生的反射区域高度范围一般在200—340 km,假设沿z轴垂直向上为正方向,水平方向正北为y轴正方向,水平向西为x轴正方向.计算区域的范围在垂直方向延伸400 km.为了降低计算量对计算机内存的要求,本文的数值模拟将电离层剖面的尺寸压缩为实际尺寸的1/20.

图3 电磁波加热电离层传播模型Fig.3.Ionospheric propagation model heated by electromagnetic wave.

2.4 数值仿真参量

在z=50 km 处通过连接边界,采用线极化的调制高斯脉冲作为入射源,Ex=1.5 sin(ω0t)exp[-(z-50×103)/108]V/m.电磁波在电离层的传播过程中发生模式转换进而产生Langmuir 扰动现象,必须满足两个条件:1)入射波频率应当略小于 F2层的最大临界频率[23,24];2)在临界层内存在等离子体密度或者电场强度的扰动[25].根据所给参数,计算出 F2层最大截止频率fmax≈6.33 MHz,这里选取加热电磁波频率f0=5 MHz 以满足第1 个条件.第2 个条件是电磁波对电离层加热引起了参量的不稳定性,会使等离子体中存在静电波扰动.

在模拟计算区域中,上下边界的截断处采用一维的Mur 吸收边界.根据吸收边界原理和连接边界理论[26],在斜入射情况下空间步长改为 Δz在z方向上的投影,具体修正为如下形式:

左截断边界处

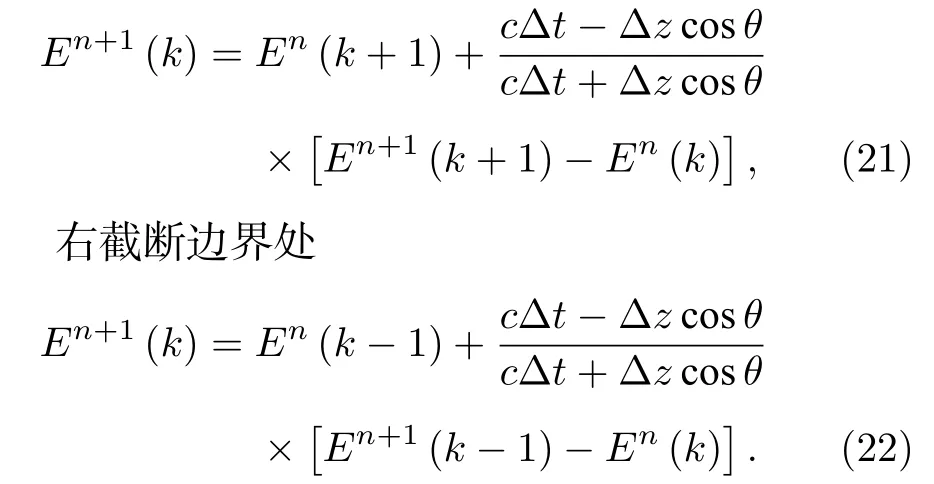
TEz波只需在原有的连接边界形式上乘以角度因子 c osθ,具体修正为如下形式:

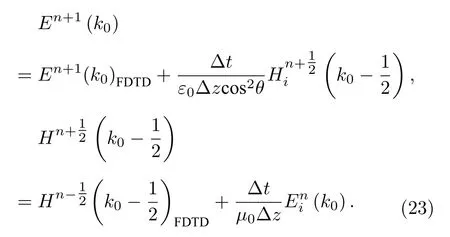
2.5 O 波、X 波和Z 波

对于高频电磁波,考虑垂直传播的波,假设电磁波传播方向k沿E1×B1方向,因此电场可能有两种基本方向(如图4 所示):E1//B0和E1⊥B0.当E1平行于磁场B0时,这种波被称为寻常(O)波[27],得到O 波的色散关系为结果表明寻常波的传播不受磁场影响.对于E1垂直于磁场B0的情况,电子响应随电场而运动,但洛伦兹力的作用使电子不能沿固定方向运动,而要产生另一方向的速度分量.为了区别于和B0无关的寻常波,把和B0有关的波动称为非寻常(X)波,非寻常波是由部分横波和部分纵波构成的电磁波.非寻常波的色散方程为

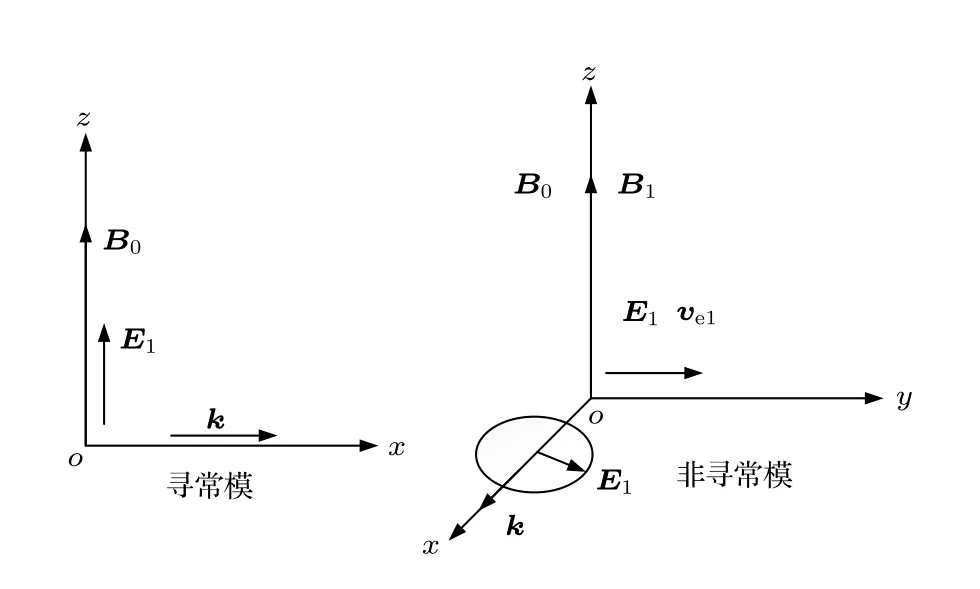
图4 O 波与X 波Fig.4.O wave and X wave.

其中n为折射率,等离子体对于扰动的响应是一个频率为的振荡,该频率称为高混杂频率.

Z 波模式是特殊(X)模式的低频分支的空间物理符号,它是等离子体的一个内模或俘获模,其频率限定在右旋截止频率WL和高混杂频率WUH之间[28].

3 模拟结果

3.1 截止和共振

为了分析波的传播特性,引入两个重要的概念:截止和共振[29].当波的折射率变为零或波数趋于零时,在等离子体中出现波的截止.由O 波的色散关系式知,波数趋于0 时其截止频率等于电子等离子体频率wpe,当w＞wpe时,O 波可以在等离子体中传播.由(24)式得,X 波在n2=0 ,k=0 情况下截止,因为n2＜0 使得波传播因子变为振幅衰减因子,意味着波在介质中传播时很快衰减,最终被截 止.而在n2→∞,k→∞条件下w与k无关,这样相速度、群速度都为0,波不能传播,出现共振.在截止点和共振点,波都不能传播,一般来说波在截止点被反射,在共振点被吸收.

令n2=0 求解(24)式,w方程应该有4 个根,其中只有两个根是合理的(w＞ 0),它们的截止频率分别称为左旋、右旋截止频率,如图5 所示.

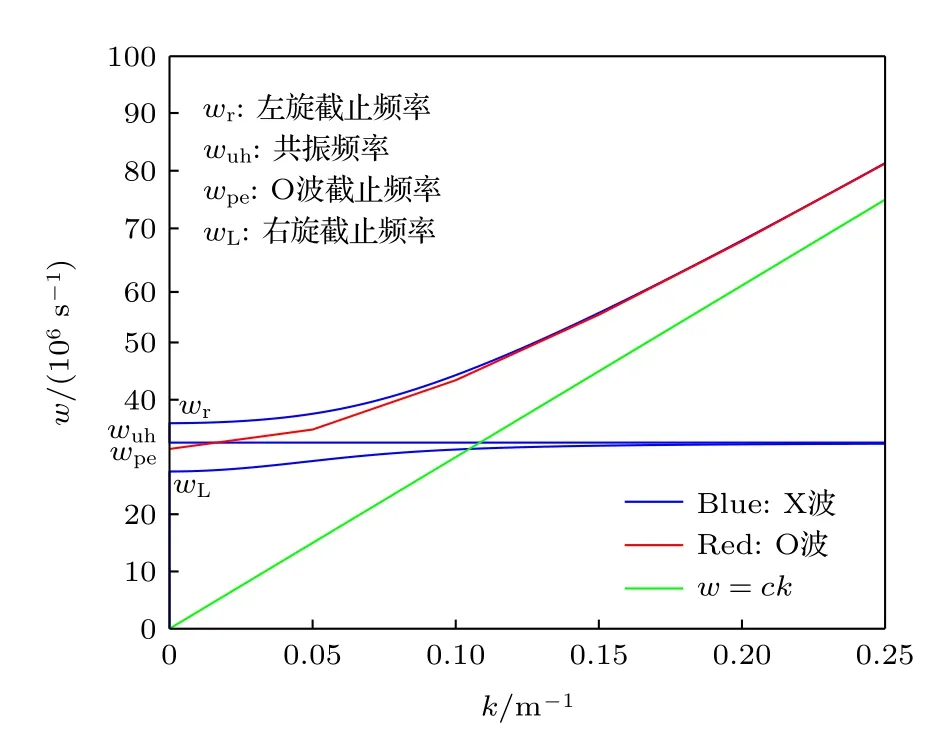
图5 w-k 色散曲线Fig.5.w-k dispersion curve.

通过对O 波和X 波的色散分析可知,对于O 波,当 0＜w ＜wpe时不能传播,w＞wpe时才能传播.对于X 波,在 0＜w ＜wL和wUH＜w ＜wR两 个频率区域不能传播,不能传播的频区称为截止带;当wL＜w ＜wUH和w＞wR时,X 波可以传播,对应的频区称为传播带.

3.2 斜入射下的电磁波传播特性

通过数值仿真模拟斜入射角为7°时的电离层传播情况,结果如图6 所示.本文数值模型的计算是在激励源(50 km,图6 粉色圆点处)加热一段时间后开始进行,电场的初始值在下边界是一个沿着x方向线性极化的波,在进入电离层等离子体区域前先经过一段中性大气(50—85 km,红色虚线区域),该传播过程中包络形状不变.

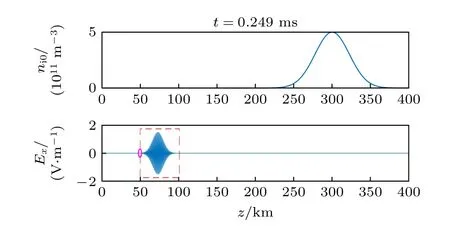
图6 背景电子密度及t=0.249 ms 时刻电场 E x 分量幅值分布Fig.6.Background electron density and amplitude distribution of electric field E x component at t=0.249 ms.

入射波在电离层等离子体中传播一段距离后出现了y方向上的分量,如图7 所示,这是由法拉第旋转现象引起的,并且电场y分量的包络形状与入射波基本一致.

图7 背景电 子密度 及t=0.821 ms 时刻电 场 E x 和 E y 分量幅值分布Fig.7.Background electron density and distribution of electric field E x and E y component amplitude at t=0.821 ms.

如图8 所示,随着等离子体密度的增加,电磁波的波形开始发生变化,X 波反射点大约在271 km处(红点所示),电磁波逐步接近X 波反射点的过程中,会导致波包出现分界点.

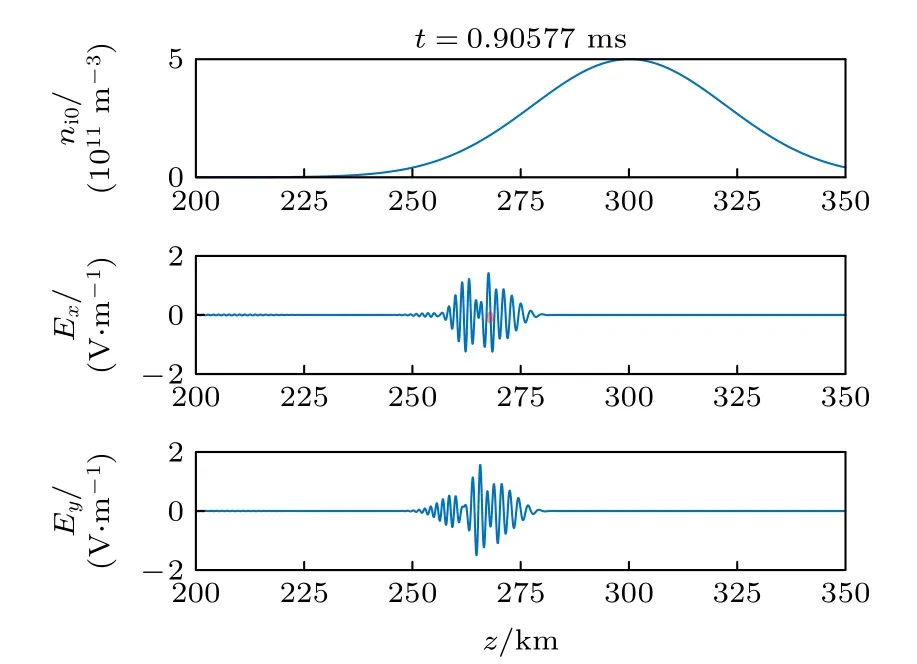
图8 背景电 子密度 及t=0.90 ms 时刻电 场 E x 和 E y 分量幅值分布Fig.8.Background electron density and distribution of electric field E x and E y component amplitude at t=0.90 ms.

在达到X 波反射点后还有O 波继续向前传播,O 波在接近其反射点的过程中逐渐从左旋圆极化变成沿地磁场方向的线极化,图9 所示的O 波反射点附近激发出了明显的z向局部振荡的电场分量.从图9 可以明显看出,大约在278 km 附近有明显的截止特征,该处为O 波的反射点,与根据Appleton-Hartree 公式计算所得的O 波反射高度相符.

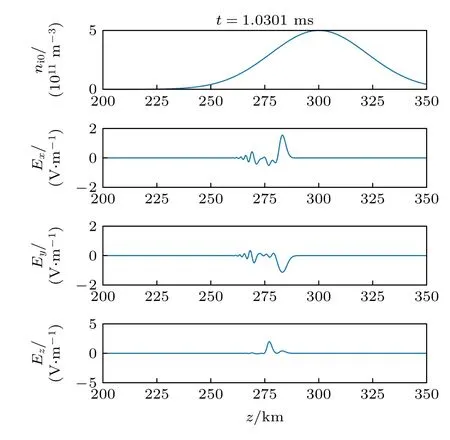
图9 背景电 子密度 及t=1.03 ms 时刻电 场 E x ,E y 和Ez分量幅值分布Fig.9.Background electron density and distribution of electric field E x ,E y and E z component amplitude at t=1.03 ms.

由图10 可以看出,z向分量电场大约在1.2 ms之后到达O 波反射区域,并形成驻波.图11 是在O 波转换区域(277—280 km)以及更高区域(310—320 km)随时间变化的静电扰动及电子密度(ns=ne-ni0)图像.

图10 背景电子密度及t=1.27 ms 时刻电场 E x ,E y 和Ez分量幅值分布Fig.10.Background electron density and distribution of electric field E x ,E y and E z component amplitude at t=1.27 ms.

从图11(a)可以看出,大约在1.2 ms,有参量不稳定性引起的静电波扰动导致O 波转换为Z 波,并向电离层的更高区域传播.图9 中电场在O 波反射点附近的快速振荡也是由于参量不稳定性过程中的Langmuir 波造成的,即高频Langmuir波的连续振荡引起电子运动.如图11(b)所示,在相互作用区域周围越来越多的电子参与波的相互作用.从图11(c)可以明显看到O 波以上,位于314—316 km 之间依然有波的存在,此处为Z 波的转换区域[30].从图11(c)可以看出在Z 波反射区域,其电场分量的高度非常窄,这里是Z 波经过参量不稳定性激发出的短波段Langmuir 波,对应的电子密度如图11(d)所示.

图11 O 波转换 区域的 静电扰动及 ns 扰 动 (a) O 波转换区域 | Ez| 变 化;(b) O 波转换区域 | ns| 变 化;(c) Z 波转换区域 | Ez| 变 化;(d) Z 波转换区域 | ns| 变 化Fig.11.Electrostatic disturbance and ns disturbance in O-wave conversion region:(a) Variation of O-wave conversion region with respect to | Ez| ; (b) variation of O-wave conversion region with respect to | ns| ;(c) variation of Z-wave conversion region with respect to | Ez| ; (d) variation of Z-wave conversion region with respect to | ns| .

4 结论

通过二维麦克斯韦方程等价转换成一维麦克斯韦方程组,与双流体力学方程进行联立,建立了斜入射电离层等离子体的数值模型,模拟了大功率电磁波在较小倾斜角度加热电离层情况下O 波的参量不稳定性.结果表明:在毫秒量级的时间尺度内,大功率高频电磁波在小角度的斜入射加热下,O 波反射区域有参量不稳定性引起的静电波扰动,O 波发生明显的衰减并激发了Langmuir 波的形成以及Langmuir 扰动所引起的O 波转换为Z 波现象.其中,Z 波在1.2 ms 左右到达O 波反射区域并形成驻波.