激发态丰质子核的双质子发射*

邢凤竹 崔建坡 王艳召3)† 顾建中

1) (石家庄铁道大学数理系,石家庄 050043)

2) (石家庄铁道大学应用物理研究所,石家庄 050043)

3) (中国原子能科学研究院,北京 102413)

1 引言

20 世纪60 年代,前苏联核物理学家Goldansky[1,2]指出,位于质子滴线外侧的原子核可能存在双质子(2p)发射.1983 年,美国劳伦斯伯克利国家实验室的科研人员[3]从22Al 的β 衰变后的激发态子核中首次发现了2p 发射,即β 缓发2p 发射(β2p).此后,人们发现了更多的β2p 发射核,如23Si[4],26P[5],27S[6]及50Ni[7]等.除通过β 衰变布居激发态,人们利用核反应手段从14O[8],17,18Ne[9-12]等核的激发态中观察到了2p 发射现象.但Goldansky 预言的2p 发射与上述激发态的2p 发射有所不同.他预言的是核基态2p 发射,其衰变寿命约大于10—12s,且发射道能级比单质子(1p)发射子核能级低,又叫做真正的2p 发射[1,13].由于对关联效应,只有偶Z核才有可能发生真正的2p 发射,所以,那些核的1p 发射道是禁戒的.然而,在实验上产生滴线附近的核是非常困难,以致于长期以来人们没有观测到真正的2p 发射.2002 年,法国国家重离子加速器和德国重离子研究中心的科研人员各自独立地从45Fe 的基态中观测到了真正的2p 发射现象,观测到的2p 发射数分别为12 个和3 个,半衰期 分别为之后,人们又陆续合成了更多的基态2p 发射核,如48Ni[16-19],54Zn[20,21]和67Kr[22],并观测到它们的2p 发射的半衰期为ms 量级,寿命较长.到目前为止,长寿命的基态2p 发射核只发现了这4 个.此外,实验上人们还发现了若干个短寿命的基态双质子发射核,如6Be[23],12O[24-27],16Ne[25,28]及19Mg[29],它们的半衰期大约为ps 量级.

自2p 发射现象被预言以来,人们提出了多种模型来描述2p 发射的物理过程.一般情况下,2p 发射可用如下3 种图像来描述[30-32]:1) 认为两个质子的关联很强,形成一个1S0准束缚态后被发射出来,然后两个质子再分开,即“2He”结团发射;2) 假设核芯与两个核子同时分开,两个发射出来的质子仅与末态相互作用有关,也就是三体发射;3) 认为是两次级联的1p 发射,即初态核先发射一个质子到中间态,然后发射一个质子到末态.由于前两种机制与核结构相关,所以它们自然就成了人们关注的对象.通过测量发射出的两个质子间的动量和角关联,可以获得核子波函数的具体形态及核子间的相互作用等信息,因而双质子发射对质子滴线核结构的研究有着极其重要的意义[33].另外,2p 发射过程与天体核演化中的(2p,γ)和(γ,2p)过程密切相关,因此,对核天体物理的研究也非常重要[34].所以,2p 发射的研究成了当前核物理研究领域中备受人们关注的前沿课题.

在理论研究方面,人们通过考虑核形变、连续态及组态混合等物理因素,发展了多种用于2p 发射的理论方法,不同程度地再现了2p 发射半衰期的实验数据[35-45].2017 年,Gonçalves 等[46]将有效液滴模型(effective liquid drop model,ELDM)推广至基态2p 发射研究,计算得到的半衰期与实验数据符合得很好.2020 年,我们在Gonçalves 等研究工作的启发下,通过引入参数化的谱因子,将推广的液滴模型(generalized liquid drop model,GLDM)用于基态2p 发射的半衰期的计算,发现计算结果也能很好地符合实验数据[47,48].在利用这两个模型的计算过程中,将2p 发射视作2He 结团的衰变过程,类似于核内阿尔法粒子的衰变[49,50].我们知道,除基态原子核外,一些处于激发态的原子核也会发生2p 发射现象.最近,我们利用统一裂变模型(unified fission model,UFM)系统地研究了激发态原子核2p 发射的半衰期,发现计算结果可以很好地再现实验数据[51].那么,ELDM 和GLDM 是否适用于激发态原子核的2p 发射研究就成了值得探讨的问题.人们多年来积累的激发态原子核2p 衰变的实验数据[8-12,52-56]便为检验ELDM 和GLDM 的预言能力提供了很好的场所.

基于上述分析,本文在Gonçalves 等[46]和我们以前的研究工作[47,48,51]的基础之上,将ELDM 和GLDM 推广至激发态原子核的2p 发射研究.本文第2 节主要介绍理论模型的基本框架;第3 节是计算结果与讨论;最后是总结.

2 理论方法简介

2.1 ELDM 简介

ELDM 将带电粒子的发射视作超非对称裂变,可以很好地描写阿尔法衰变、结团发射、冷裂变和质子发射等物理过程[57-62].该模型用两个相交的球来表示在衰变过程中的变形核的形状.为了描述该物理过程,该模型引入了4 个独立的变量:R1,R2,ζ和ξ.其中R1和R2分别是发射粒子和子核的半径,ζ和ξ分别为发射粒子和子核的几何中心之间的距离以及子核与发射粒子之间的距离,见图1.

图1 母核衰变过程中发射粒子和子核形状示意图Fig.1.Schematic representation of the configuration of the emitted particle and daughter nucleus.

这4 个变量要受到3 个约束条件的限制.首先,为了保持在形变过程中两个球始终接触,必须满足如下几何关系:

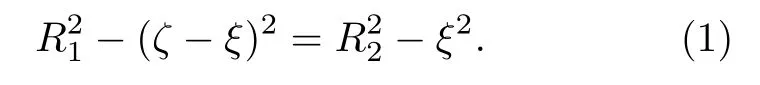
另外,计算中假设核物质不可压缩,因此,整个系统在形变过程中体积守恒,可用下式来表示:

式中R0为母核的电荷半径,由计算得到,r0是核半径参数.随着两个核(子核和发射粒子)几何中心距离的增加,该分子形状的形变核最终达到两个核球面相切的临界状态.此时,发射粒子和子核的半径分别为

第3 个约束条件是假定在核发生形变的过程中,发射粒子和子核的质量保持不变.在此条件下,发射粒子的半径由下式确定:

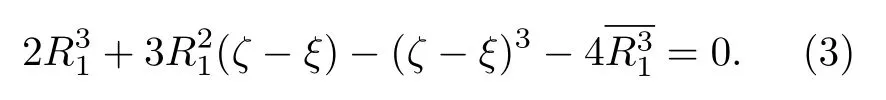
此外,模型中假设母核、子核和发射粒子核电荷密度相同,发射粒子和子核的终态半径可表示为

通过上述3 个约束条件,衰变过程可以简化为一维势垒穿透问题.根据量子隧穿理论,放射粒子的穿透概率可由下式计算:

式中,V(ζ) 为一维总有效液滴势垒,Q为衰变能,µ为惯量系数,在本文的计算中,用的是Werner-Wheeler 型惯量系数,积分的上下限ζ0和ζc分别是入射点和出射点,由方程V(ζ)=Q来确定.

2p 发射的半衰期为

其中ν0为2He 结团碰撞势垒的频率.由上述介绍可知,该模型只有两个参数,即r0和ν0,它们由拟合基态2p 衰变的实验数据得到.在计算过程中,这两个参数分别取1.12 fm 和4.96×1019s—1[46].

2.2 GLDM 简介

GLDM 假定原子核的密度为常数,且原子核液滴在形状演化过程中体积守恒,那么在原子核形状演化过程中体系的总能量为[63]

其中,EV,ES,EC,EN和El分别表示体积能、表面能、库仑能、亲和能和离心势能.当原子核处于球形基态时,不存在亲和能和离心势能.EV,ES和EC的具体形式为

其中,I0=(N0-Z0)/A0为母核的相对中子过剩,V(θ)是体表面的静电位.

当两体分开时,EV,ES,EC,EN和El分别表示为

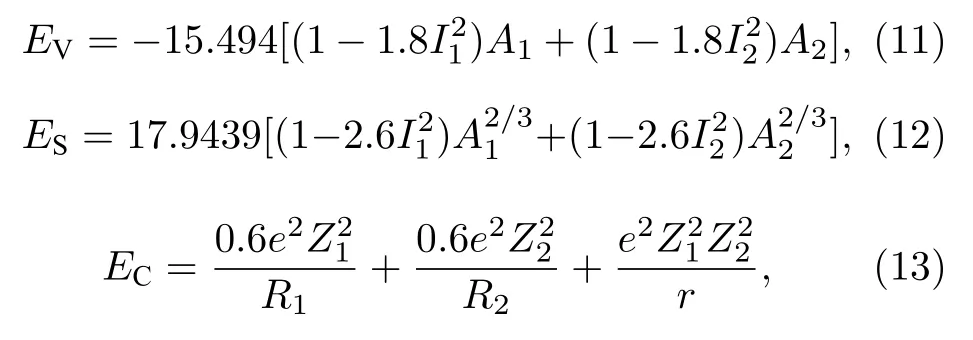
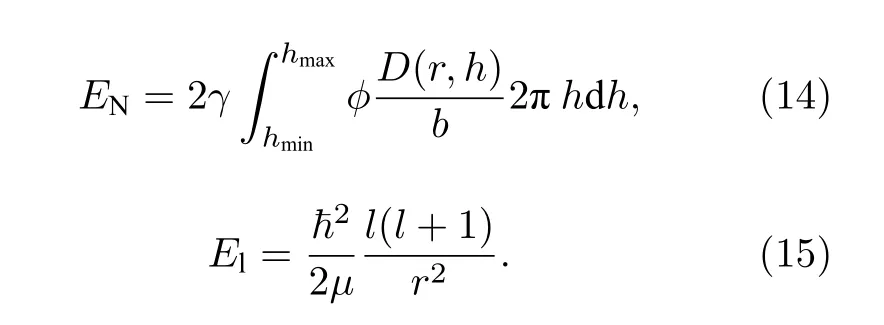
其中,Ai,Zi,Ri和Ii(i=1,2) 分别表示两个裂变碎片的质量数、电荷数、电荷半径和相对中子过剩.而电荷半径可由下式计算得到

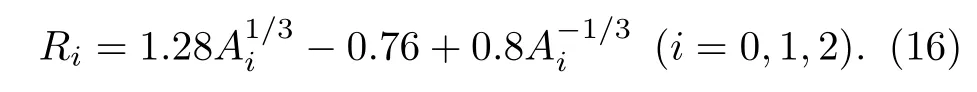
在(14)式中,h是垂直于裂变轴的圆面半径;D是间隙处两个相对半空间的两个无穷小表面之间的距离;b是表面宽度;ϕ是Feldmeier 函数;表面参数γ是两个核的表面参数的几何平均,取为如下形式:

此时,亲和能与表面弥散无关.而且,当颈部不存在时,亲和能变为0.由于亲和能的存在,在大形变处出现一个很宽的包,而且几乎是一个常数.研究形变时,库仑力和亲和力之间的平衡控制着位垒的高度和位置.亲和力能使位垒的高度降低几个MeV 并能移动位垒的位置.

在WKB 近似下,穿透概率P可以表示为

由于在两碎片断点之前的形变能(相对于球形)很小或为负,所以对2p 发射做出如下近似:Rin=R1+R2和B(r)=µ=A1A2/A.Rin为入射点,µ为有效质量.出射点Rout可表示为

其中Q为衰变能.

2p 发射的半衰期的表达式为

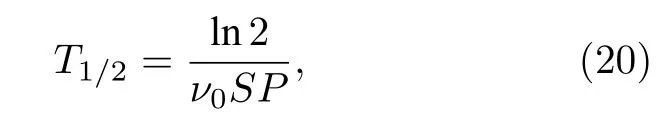
其中,ν0为2He 结团碰 撞位垒 的频率,S为核内2He 结团的谱因子.在计算过程中,ν0由如下经典方法计算得到

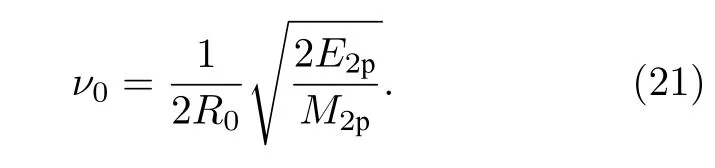
式中,R0为母核的电荷半径,E2p和M2p分别为2He 结团的动能和质量.

S可由如下参数化的公式得到:

其中,G=(2n)!/[22n(n!)2],n为主质子谐振子量子数的平均值,其值由表达式n≈(3Z0)1/3-1 来确定.此处,A0和Z0分别为母核的质量数和电荷数.χ2为质子重叠函数,其值由拟合19Mg,45Fe,48Ni和54Zn 基态2p 发射的实验数据得到[47,48].

3 计算结果与讨论

首先,利用ELDM 和GLDM 两个模型计算了14O*,17,18Ne*,22Mg*,29S*和94Ag*(“*”表示原子核处于激发态)的2p 发射半衰期,并与实验数据进行了对比,如表1 所列.表1 中,第1 列和第2 列分别为原子核的初态和末态,第3 列和第4 列分别为原子核初态与末态的自旋和宇称,第5 列l为2p 发射过程中带走的轨道角动量(其值由选择定则来确定),第6 列和第7 列分别为衰变能和半衰期的实验数据,第8 列和第9 列分别是利用ELDM和GLDM 计算得到的对数半衰期(以下半衰期均为对数半衰期),最后一列是利用UFM 计算的结果[51].对于14O,Bain 等从激发能为7.77 MeV 的2+态上观察到了2p 发射现象,但其衰变模式以级联发射为主[8].尽管没有观察到2He 结团发射,但给出了2He 结团发射半衰期的下限,即-16.12 s[8].由表1 可知,基于ELDM,GLDM 和UFM 计算得到的结果都大于实验数据的下限,且与实验数据符合得很好.而R 矩阵理论、Sreeja 公式以及Liu 公式给出的半衰期分别为—18.12 s[8],—19.94 s[51]和—16.85 s[51],都小于实验半衰期的下限.这说明,ELDM,GLDM 和UFM 的计算精度比上述3 个方法的精度高.从20 世纪末到本世纪初,Chromik 等[9,10]对17Ne 激发态的2p 发射做了深入研究.从17Ne 的前两个激发态,即3/2—(激发能E*=1.288 MeV)和5/2—(E*=1.764 MeV)态上观察到了2p 发射现象.他们认为,5/2—态衰变到子核15O 基态的衰变模式为级联2p 发射,且未观测到3/2—态的衰变模式为2He 结团发射的实验证据[10].但是,他们给出了3/2—态2He 结团发射半衰期的下限,其值为通过比较表1 中17Ne 激发态的实验半衰期与计算值,发现由ELDM,GLDM 和UFM 计算得到的结果都能与实验数据很好地符合.除17Ne 激发态的2p 发射外,18Ne 激发态的2p 发射也受到了很多研究者的关注.在2001 年,Gomez del Campo 等[11]通过17F与1H 的核反应生成了18Ne 激发态,并从它的1—态(E*=6.15 MeV)中发现了2He 结团发射的有力证据.但受实验条件的限制,他们没能将2He 结团发射和直接三体发射区分开来.之后,Raciti 等[12]在意大利南方国家实验室FRIB 装置上开展的新实验将1—态上2p 发射的机制进行了鉴别.他们发现,2He 结团发射的分支比占31%,而“民主”或虚级联发射的分支比占69%.结合Gomez del Campo等[11]和Raciti 等[12]的实验结果,就可以推测出18Ne 的1—态2He 结团发射的宽度和半衰期的实验值,分别是(6.51 ± 0.93) eV 和(—16.15 ± 0.06) s.表1 中,ELDM,GLDM 和UFM 给出的18Ne 的1—态的半衰期分别为—16.34,—17.20 和—16.79 s.利用R 矩阵方法计算的该激发态的半衰期为—17.12 s[11].通过理论值与实验数据对比,很容易看出ELDM 的计算结果与实验数值很接近,精度最高,UFM 次之,而GLDM 和R 矩阵方法的计算精度就稍差一些,但仍在可接受范围之内.这是在计算过程中,假定18Ne 的基态与激发态的谱因子相同造成的.事实上,激发态与基态原子核的谱因子不同.若考虑两种状态之间的差异,则可以改善理论值与实验值之间的符合程度.

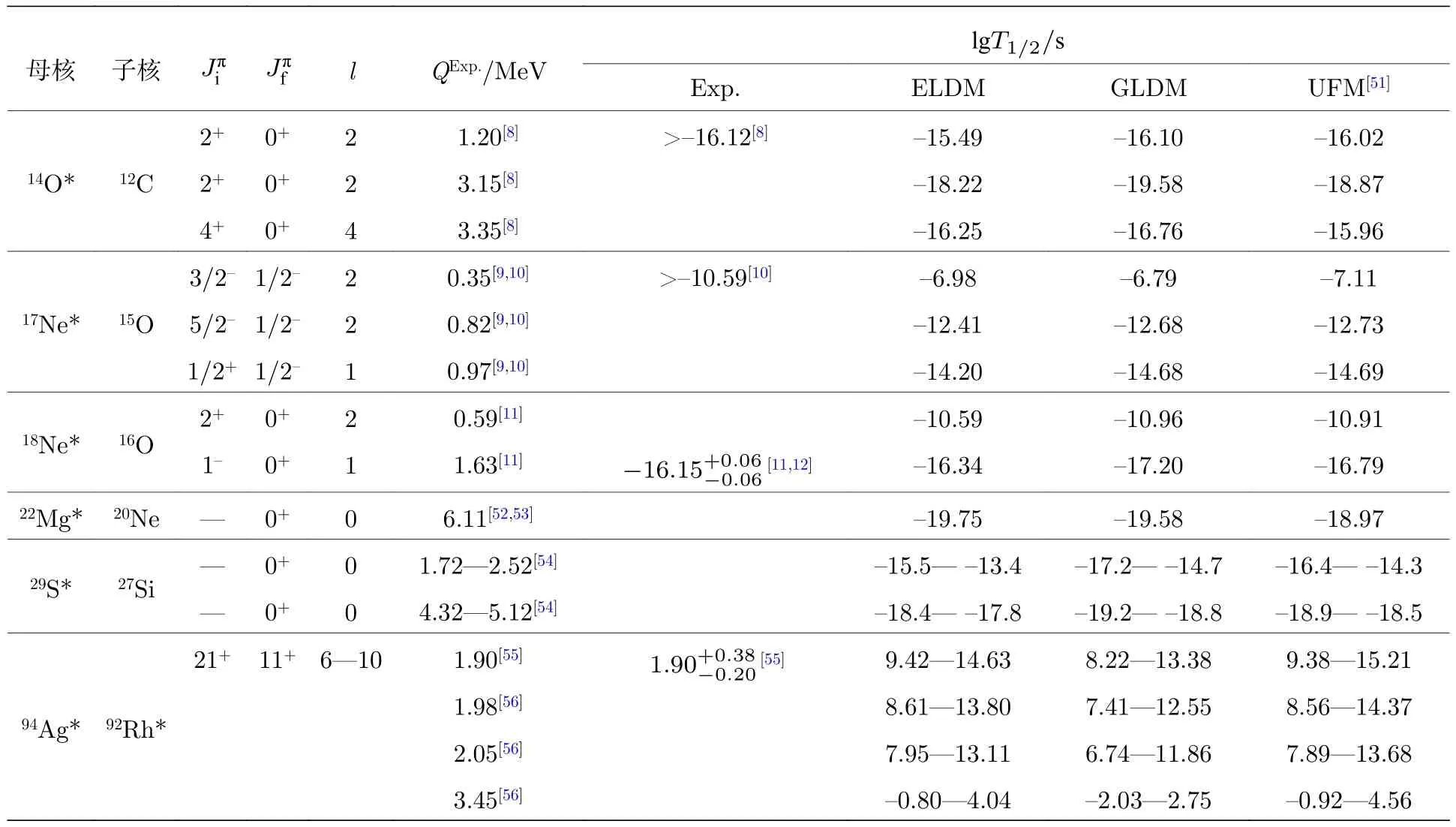
表1 激发态原子核2p 发射半衰期的理论计算结果与实验值的比较Table 1.Comparison between the experimental 2p decay half-lives of excited states and those within different models.

近年来,94Ag 的21+激发态的质子放射性备受人们关注.2005 年,Mukha 研究组[64]观察到了21+态衰变到子核激发态的1p 发射现象,并发现1p 发射宽度急剧压低,表明21+激发态是形变态.2006 年,Mukha 研究组[55]又从94Ag 的21+激发态中观察到了衰变到子核激发态的2He 结团发射,该2p 发射的衰变能和半衰期分别为1.9(1) MeV 和1.90 s.他们进行理论分析时发现,只有假设21+态具有非常大的长椭球形变,才能解释实验上所观测的大的2p 衰变分支比,即0.5(3)%.但Pechenaya等[65]却没有观测到94Ag 的21+激发态的2p 发射,对Mukha 的实验提出了质疑.为了揭示94Ag 的21+激发态的本质和可能存在的衰变模式,Kankainen研究组[56]利用潘宁阱质谱仪JYFLTRAP 测量了2p 衰变子核92Rh 以及β 衰变子核94Pd 的质量.他们把测量结果和Mukha 等测量的1p 和2p 衰变的实验数据放在一起分析,发现21+态的激发能为6.96 或8.36 MeV.利用这两个不同的激发能数值和AME2003 核质量表的相关数据,得到了3 个不同的Q值,即2.05,3.45和1.98 MeV[56].将这3 个不同的Q值分别输入到ELDM 和GLDM 模型中计算,就可以得到2p 衰变的半衰期.在计算过程中,l值取6 ℏ —10 ℏ[55].从表1 可以看到,只有当Q为3.45 MeV 时,ELDM和GLDM 的计算结果才能与实验半衰期符合,这与UFM 情况下的结果一致.

通过上述分析可知,ELDM 和GLDM 可以自然地推广到激发态原子核的2p 发射研究.因此,用这两个模型对目前尚未观测到的一些激发态的2p 发射的可能性做了理论预言,如表1 的第8 列和第9 列所列.这些理论预言可以为将来寻找新的2p 衰变态提供参考.对于22Mg 和29S 激发态的2p 发射[52,54],由于初态的自旋-宇称未知,所以在计算时l的值取为0.另外,表1 的最后一列给出了UFM 的预言结果.通过比较可以看出,ELDM和GLDM 预言的半衰期与UFM 预言的很接近.这是由于这3 个模型都把2p 发射当作2He 结团穿透势垒的量子过程来处理造成的.所以,能够描写阿尔法衰变过程的模型应该可以用于激发态原子核的2p 发射研究.

由于22Mg,29S 和94Ag 激发态的Q和(或)l值尚未确定,因此以94Ag 的21+激发态为例,将不同的Q值输入到ELDM 和GLDM 中,考察半衰期对l值的依赖程度.半衰期随l值的演化曲线如图2所示.可以看出,不仅这两个模型的演化曲线类似,而且相同条件下半衰期的数值比较接近.由于这两个模型离心势的形式相同,且都与l呈l(l+1) 的变化规律,因此导致半衰期随l值的演化曲线不仅相同,而且半衰期与l值之间表现为二次函数关系.文献[51]的研究工作可以证明这一点.其次,从图2还可以看出,半衰期对Q值的依赖很敏感.例如,当Q值从2.05 MeV 变化至3.45 MeV 时,半衰期竟增长了约8 个数量级,进一步表明精确测量核质量和激发能的重要性.第三,如果94Ag 的21+激发态确实存在2p 衰变且Mukha 测量的半衰期准确,则根据图2 可确定出在2p 衰变过程中,2He 结团带走的l值为8 ℏ .

图2 用ELDM 和GLDM 计算的94Ag 的21+激发态的2p 发射半衰期随l 的演化情况,阴影区域为半衰期的实验数据Fig.2.The 2p decay half-lives of the 21+ isomeric state of 94Ag within the ELDM and GLDM as functions of l.The shaded area stands for the experimental half-life.

最后,需要说明的是,2009 年,Cerny 等[66]对94Ag 的21+态的衰变模式再次进行了研究,这是目前最新的关于94Ag 的21+态衰变的实验研究工作.但他们没有从该激发态中发现2p 发射存在的实验证据.不同实验组之间相互矛盾的测量结果[55,56,65,66]和Mukha 等[67]与Pechenaya 等[68]之间的争论表明94Ag 的21+态是否存在2p 发射仍是一个未解之谜.此外,人们从17Ne 和18Ne 的高激发态中也观察到了2p 发射现象[12,69].对于17Ne,激发能大于2 MeV 的一个或多个的高激发态会以2He 结团的形式进行衰变[69].对于18Ne,它的高激发态则以民主或级联2p 发射的衰变模式为主[12].但这两个核的高激发态的2p 发射尚未进行进一步的测量.为了解决上述问题,就需要实验学家利用新一代的放射性束流装置进行高精度的实验观测.我国正在建造的强流重离子加速器(high intensity heavy-ion accelerator facility,HIAF)便为解决这些问题提供了良好的机遇[70].另一方面,需要理论学家考虑更多的物理因素,如张量力[71]、三体力[72]和精确的对力[73],发展新的微观方法,对激发态的2p 发射作更加合理的描述.总之,研究激发态原子核的2p 衰变可获得更多的核结构的信息,尽管这种2p衰变很难观测到,但十分值得人们做进一步研究.

4 结论

本文首先将ELDM 和GLDM 推广至14O*,17,18Ne*,22Mg*,29S*和94Ag*的2p 发射半衰期的计算.然后,利用这两个模型对目前尚未观测到的一些激发态的2p 发射的可能性进行了理论预言.最后,以94Ag 的21+激发态的2p 发射为例,讨论了Q值和l值的不确定性对其半衰期的影响.通过分析本文的计算结果,比较与UFM 计算结果的差异,并结合当前2p 发射的研究进展,可以得到如下结论:

1) ELDM 和GLDM 都能较好地符合所有的2p 发射半衰期的实验数据.尽管GLDM 模型中引入了参数化的谱因子,但在计算过程中仍认为激发态谱因子与基态一致,导致计算结果与实验数据之间有了一定的差别.若考虑激发态谱因子与基态谱因子的差异,则能提高GLDM 的计算精度.

2)由于ELDM,GLDM 和UFM 这3 个模型的物理机理类似,导致其预言的半衰期彼此接近,这些预言可以为将来实验上寻找新的2p 衰变态提供参考.

3) 根据Mukha 等测量的94Ag 激发态的半衰期[55],可以定出在2p 衰变过程中带走的l值为8 ℏ .由于Q值和l值具有一定的不确定性,导致二者对94Ag 激发态的半衰期有重要影响.对于l,半衰期与l之间呈二次函数关系.对于Q,当Q值从2.05 MeV 变化至3.45 MeV 时,半衰期增长了约8 个数量级,进一步表明精确测量核质量和激发能的重要性和必要性.

4)94Ag 的21+激发态是否存在2p 发射仍是未解之谜.17Ne 和18Ne 的高激发态的2p 发射尚未得到进一步检验和精确测量.要解决这些问题,不仅需要利用新一代的放射性束流装置进行实验观测,还需要考虑更多的物理因素,发展新的微观方法.