石墨烯中选择性增强Kane-Mele 型自旋-轨道相互作用*

白占斌 王锐 周亚洲 吴天如 葛建雷 李晶 秦宇远 费付聪 曹路 王学锋 王欣然 张帅孙力玲 宋友‡ 宋凤麒††

1) (南京大学物理学院,固体微结构国家重点实验室,人工微结构科学与技术协同创新中心,南京 210093)

2) (中国科学院物理研究所,北京凝聚态物理国家研究中心,北京 100190)

3) (中国科学院上海微系统与信息技术研究所,信息功能材料国家重点实验室,上海 200050)

4) (南京大学化学化工学院,配位化学国家重点实验室,人工微结构科学与技术协同创新中心,南京 210093)

5) (南京大学电子科学与工程学院,固体微结构国家重点实验室,人工微结构科学与技术协同创新中心,南京 210093)

1 引言

量子自旋霍尔效应[1-4]最早在石墨烯体系中提出,随后在HgTe/CdTe 量子阱[3]、InAs/GaSb异质结[4]、单层FeSe[5]、单层WTe2[6,7]等系统中实现.在石墨烯中实现量子自旋霍尔效应的关键在于将石墨烯的化学势调控到狄拉克锥处由自旋-轨道相互作用打开的带隙中.然而石墨烯中内禀的自旋-轨道相互作用十分微小,所打开的能隙仅有10—5—10—6eV[8,9].因此尽管目前做出了大量的尝试去打开石墨烯狄拉克点的能隙,却依然没有突破性的进展.目前提出的增强自旋-轨道相互作用的方案主要有:用氢原子功能化石墨烯(氢化石墨烯[10]、氟化石墨烯[11]),用In[12],Au[13,14],Ir[15]等金属原子[16]修饰石墨烯表面,以及将石墨烯与强自旋-轨道耦合材料结合形成异质结,如Bi2Te2Se,Bi2Se3等拓扑绝缘体[17]和一些过渡金属硫族化物[18,19],可以将石墨烯中的自旋-轨道相互作用提高到10—2eV的量级[10,13,14,16,17].

但要想获得可靠的量子自旋霍尔态,石墨烯中所引入的自旋-轨道相互作用须是Kane-Mele(KM)型,其哈密顿量为～τzσzsz,而Bychkov-Rashba(BR)型自旋-轨道相互作用 (～(s×σ)z) 会使能带中空穴分支发生劈裂,抬高价带使能隙变小,甚至于使不同的电子和空穴分支接触到一起,从而破坏量子自旋霍尔态的输运[8].这里τ,σ,s都是Pauli矩阵,τz=±1 对应于动量空间K(K′)点,σz=±1对应于A(B)两套子晶格,sz对应于电子的自旋.考虑到KM 型自旋-轨道相互作用源于石墨烯六角蜂窝状晶格的对称性,实现这种有选择性的自旋-轨道相互作用增强存在困难也在情理之中,因为在修饰石墨烯的时候必然会给这种周期性的晶格结构带来额外的杂质原子.因此,即使能够引入微弱的KM 型自旋-轨道相互作用,往往会伴随着更大的非对称Rashba 型自旋-轨道相互作用,且其引入的杂质也可能影响到石墨烯的迁移率并破坏脆弱的量子自旋霍尔边缘态.

本文以Na[Dy(EDTA)(H2O)3]·5H2O (EDTADy 分子)修饰石墨烯,不仅提高了石墨烯器件的输运性能,并且提出一种耦合机制,即电子自旋与弯曲的声子相互耦合,从而在石墨烯中引入了类似于KM 型的自旋-轨道相互作用.按照Elliot-Yafet(EY)机制[20,21],由电子自旋弛豫时间可以得到所引入的自旋-轨道耦合强度.修饰后的石墨烯中量子霍尔效应也得到提升.

2 实验方法

石墨烯器件是在用化学气相沉积法生长的单晶石墨烯基础上加工而成的(如图1(a)所示).将单晶石墨烯转移到表面为300 nm 厚的二氧化硅绝缘层的硅片上.通过标准电子束曝光工艺和电子束蒸发沉积金属电极形成Hall-bar 器件.EDTADy 分子是根据已有文献报道合成[22].将10 mL EDTA-Na2(7.44 g,0.02 mol)的水溶液搅拌加入到10 mL Dy(NO3)3·5H2O (8.77 g,0.02 mol)水溶液中,然后利用1 mol/L 的NaOH 水溶液将其pH值调为6.5.通过拉曼光谱、原子力显微镜和电学输运测量可以研究EDTA-Dy 修饰对石墨烯的影响.电输运测量是利用标准的锁相技术,在Cryomagnetics 公司的C-Mag 系统中进行.首先测量纯石墨烯,然后将0.1 mL EDTA-Dy 分子溶液滴在器件表面,置于通风橱中几分钟使水分挥发,之后再次测量.面内磁场的测量是在矢量磁体中进行的.一些电学输运的参数包括:载流子浓度n=1/(qRH),其中q为载流子电荷,RH为霍尔系数,可通过低磁场下霍尔电阻线性拟合得到;载流子迁移率可以通过µ=σ/(nq) 得到,其中σ是石墨烯电导;平均自由程和扩散系数分别为和D=υFle/2 ,其中费米速度υF≈106m/s .

图1 EDTA-Dy 修饰的石墨烯器件及其输运特性 (a)石墨烯介观输运结构图,用橘色小球代表EDTA-Dy 分子修饰在石墨烯上面;(b) EDTA-Dy 分子修饰的石墨烯的拉曼光谱;(c)在2,20 和290 K 温度下,EDTA-Dy 修饰石墨烯的电阻随门电压的变化;(d) 在温度2 K 和磁场12 T 的 条件下,分子修饰后的石墨 烯的纵向电阻 ρ xx 和霍尔电导 σ xy 随门电 压的变化Fig.1.The EDTA-Dy dressed graphene and its device transport:(a) Schematic configuration of the device,where the EDTA-Dy(orange balls) coats the graphene sheet;(b) Raman spectrum of EDTA-Dy dressed graphene,indicating that the sample is a single layer graphene sheet;(c) resistance as a function of back gate voltage (Vg) for EDTA-Dy dressed graphene at 2,20 and 290 K;(d) Vg dependence of the longitudinal resistivity ρ xx and the Hall conductivity σ xy measured in a magnetic field of 12 T at a temperature of 2 K,where the Hall conductivity goes quantized and the longitudinal resistivity approaches zero.

3 实验结果与讨论

3.1 EDTA-Dy 分子修饰石墨烯的输运性能

图1(b)是EDTA-Dy 修饰的石墨烯的拉曼光谱,2D 峰与G 峰的峰高比为1.44,2D 峰半高宽25.01 cm—1,这表明样品是单层石墨烯.图1(c)是EDTA-Dy 修饰的石墨烯在不同温度(2,20,290 K)下纵向电阻Rxx随栅压Vg的变化.经过EDTA-Dy修饰后,原本p 型的石墨烯中空穴载流子浓度降低,这意味着有电子从分子转移到了石墨烯.这可从分子本身的结构来理解.EDTA-Dy 复合体的ED TA 配体中有4 个—COO—官能团螯合着中心的DyⅢ离子.—COO—官能团中自由O2—电子密度很高,其与石墨烯中π 电子有强烈的相互作用趋势.

石墨烯被修饰之后,其输运性能得到了提高,这与之前报道的Pt-porphyrins 修饰石墨烯的情况类似[23].修饰后石墨烯的载流子迁移率从1919 cm2/(V·s)提高到3626 cm2/(V·s),并表现出量子霍尔效应(图1(d)).在低温2 K 和强磁场12 T下,霍尔电 导σxy和纵向电阻ρxx随栅压Vg变 化,σxy会量子化到 4 (n+1/2)e2/h的平台,同时ρxx接近0.4 (n+1/2)e2/h的霍尔电导平台体现了单层石墨烯狄拉克费米子的量子霍尔效应的特性.

3.2 受抑制的弱局域化效应和选择性增强的KM 型自旋-轨道相互作用

电子的自旋-轨道相互作用会改变一对沿时间反演路径运行的电子的干涉,而造成电子波函数相位的改变以及低场下磁电阻曲线的量子修正[24].对于石墨烯,McCann 等[25]的弱局域化理论描述了在低场下电导的弱局域化修正:

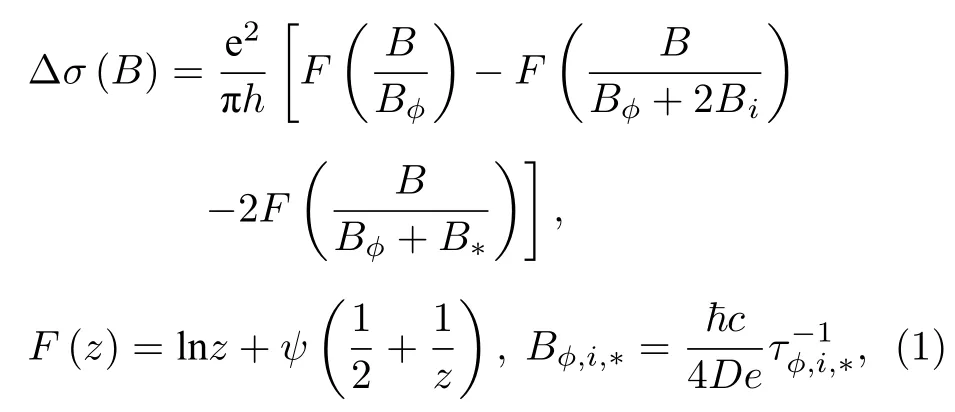
其中,ψ是Digamma 函数;D是扩散系数;是电子退相干速率;是谷内对称性破缺散射速率,是谷间散射速率,可以从低场磁电阻曲线拟合得到.相应的弛豫长度与弛豫时间的关系为McCann和Fal’ko[26,27]进一步提出,通过分析石墨烯弱局域化特征和自旋弛豫机制,可以推测出自旋-轨道相互作用的类型.当较强的自旋-轨道相互作用被引入石墨烯当中,弱反局域化增强的输运特征意味着Rashba 型自旋-轨道相互作用占主导作用,而被抑制的弱局域化现象表明KM 型自旋-轨道相互作用占主导地位.

在低温2 K 下EDTA-Dy 分子修饰前后石墨烯的低磁场输运性能如图2(a)和图2(b)所示.器件电导在零场附近迅速降低,这正是石墨烯中电子的弱局域化效应.通过调控门电压,可以分别将修饰前后的石墨烯器件中的载流子浓度调至基本相同,这样可以在相同的费米能级处来比较修饰前后石墨烯中的电子轨道相互作用的强度.在相同载流子浓度下修饰后石墨烯并没有发生弱反局域化转变,而且在扩散系数D增大的情况下,弱局域化特征稍弱于修饰前,这说明EDTA-Dy 分子覆盖在石墨烯上后弱局域化效应被抑制,这种特征恰恰与McCann 理论中KM 型自旋-轨道相互作用占主导地位的情形相吻合[26,27].因此,可认为分子修饰后的石墨烯中引入了新的电子自旋弛豫机制是本征的Kane-Mele 自旋弛豫速率),导致修饰后 的石墨烯退相干速率由原来的增强为分别为修饰前后的电子退相干速率).通过拟合分子修饰前后石墨烯的弱局域化曲线可以得到各自的电子退相干速率随门电压调控的变化.对比石墨烯被修饰前后退相干速率的差异,可以获得相应温度下EY 机制所对应的自旋-轨道耦合强度:图2(c)所示为2 K 温度下,分子修饰前后的关系,其中τp=为电子动量弛豫时间(弹性散射时间),实线和虚线分别是它们的拟合曲线.在本实验的载流子浓度范围内,两条拟合曲线的间距几乎不变,也就是说几乎保持为常数,这也验证了EY 型电子自旋弛豫机制.由两条拟合曲线外延截距的差值,可得EY 机制自旋耦合强度ΔEY约为5.2 meV.

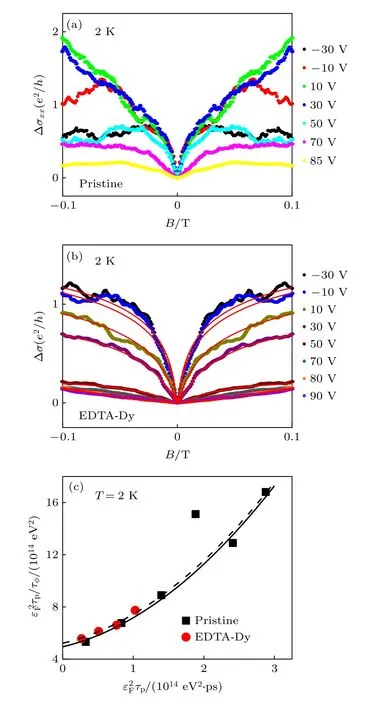
图2 EDTA-Dy 修饰石墨烯引起的被抑制的弱局域化现象及EY 机制拟合 (a),(b) 2 K 时石墨烯被修饰前后的弱局域化随门电压的调控;(c)修饰前后石墨烯中与 的关系,实线和虚线是各自的二项式拟合Fig.2.Suppressed weak-localization in the EDTA-Dy decorated graphene device and EY plot:(a),(b) Weak localization of pristine and EDTA-Dy dressed graphene at different Vg while fixing the temperature of 2 K;(c) as a function of for the pristine and EDTA-Dy dressed graphene,where solid and dashed line are the fit for them,respectively.

3.3 分子修饰后石墨烯在矢量磁场下的输运

3.2 节阐述的受抑制的弱局域化现象和EY 机制拟合结果均说明石墨烯被修饰后,其KM 型自旋-轨道相互作用被选择性地增强.这种对石墨烯表面的修饰本该引入更多的电子散射,但研究发现器件的量子输运性能得到提高,分析认为,EDTADy 分子覆盖区域的涟漪增强了石墨烯中的弯曲声子效应,并选择性增强了EY 机制的电子自旋弛豫效应.

首先通过室温下的原子力显微镜观察石墨烯的形貌.如图3(a)所示,未修饰的本征石墨烯粗糙度的均方根约为0.66 nm,而修饰并完成磁电阻的测量后,将器件表面的分子覆盖层去除,再次用原子力显微镜测量发现表面粗糙度均方根值提高到1.64 nm.这种褶皱增强现象也有其他类似的文献报道[28].这是由于石墨烯和有机分子层随温度伸缩具有不同的依赖关系.这种涟漪可能将某些区域的石墨烯从衬底上分离开,从而减小了硅片衬底对石墨烯载流子的散射,提高了迁移率[29,30].

考虑去除分子覆盖层可能会造成石墨烯表面的界面效应,我们通过矢量磁体测量磁电阻的方法来获得石墨烯修饰前后的粗糙度.根据 Lundeberg和Folk[31]提出的理论,石墨烯表面的涟漪会诱导随机的矢量势场产生,进而改变面内磁场下磁电阻的响应.对于普遍的高斯型涟漪,这种随机矢量势调节的磁电阻Δρ(B//)可以通过玻尔兹曼方法计算:

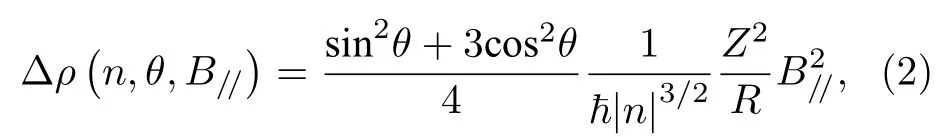
其中θ是电流方向与面内磁场方向的夹角,Z为粗糙度均方根,R为石墨烯涟漪起伏的关联长度.在该器件中EDTA-Dy 分子覆盖前后θ约为10°和80°.施加面内磁场后,通过方程(2)拟合得到修饰前后Z2/R约为0.14 nm 和0.67 nm (见图3(b)).

图3 原子力显微镜表征和矢量磁体测量的石墨烯涟漪结构 (a)未修饰的的本征石墨烯(上)和分子修饰石墨烯(下)的原子力显微镜形貌图,图中比例尺为100 nm;(b)在水平磁场下,分子修饰前后石墨烯的磁电阻随磁场强度的变化,其中实线由(2)式拟合得到,拟合参数分别为n=6.44 × 1012 cm—2 和4.27 × 1012 cm—2,插图是矢量磁体测量示意图;(c),(d)在一系列特定平行磁场B//下,修饰前后石墨烯的磁电阻对垂直磁场(B⊥＜0.04 T)的弱局域化响应;(e)拟合得到修饰前后石墨烯的退相干速率 与平行磁场 的关系,其斜率与 Z 2R 相关Fig.3.Atomic force microscope characterization and ripple configuration revealed by the vector magnet measurement.(a) Atomic force microscope images of pristine graphene (upper) and EDTA-Dy dressed graphene (down).The scale bar is 100 nm.(b) Resistivity of pristine graphene and EDTA-Dy dressed graphene dependent on The solid lines are the fitting according to Eq.(2)using n=6.44 × 1012 cm—2 and 4.27 × 1012 cm—2.The inset is the measurement configuration.(c),(d) B⊥—dependent magnetoconductivity (B⊥＜0.04 T),at a series of fixed B//.Dashed lines are the fitting according to Eq.(3).Panel (c) and (d) correspond to the graphene before and after EDTA-Dy dressing,respectively.(e) Extracted values of plotted against ,the slope is related to Z 2R .

处于面内平行磁场下,石墨烯的涟漪外形不仅会造成磁电阻的响应,还会对垂直磁场下的弱局域化现象造成影响.这是由于当平行磁场穿过涟漪时,产生的磁通量会对电子的传导施加轨道效应,因此电子相位相干导致的弱局域化会被抑制.所以我们选择在一系列特定的平行磁场下,分别测量修饰前后由垂直磁场造成的弱局域化效应,结果如图3(c)和图3(d)所示.Lundeberg 和Folk[31]提出具有涟漪的石墨烯处于平行磁场下,其磁电阻弱局域化曲线方程中的与平行磁场强度具有如下相关性:拟合弱局域化曲线可得到修饰前后的石墨烯器件中,Z2R分别为 1.07 nm3和 7.06 nm3,如图3(e)所示.

3.4 结果讨论

利用矢量磁体测量得到的Z2/R和Z2R数据,可以得到未修饰的石墨烯高斯型涟漪的粗糙度Z=0.62 nm 和关联程度R=2.7 nm,而修饰后的石墨烯Z=1.48 nm 和R=3.2 nm .这 表明石墨 烯被EDTA-Dy 修饰后确实产生了具有显著效果的涟漪.可认为这种涟漪的石墨烯具有的弯曲声子协助了EY 型的自旋弛豫.根据之前关于全对称性适应的自旋-声子耦合研究[32],与B2不可约表示相关的声子振动会引入一个电子运动的哈密顿量Hph=gσzszh(r)2,其中h(r) 是碳原子的垂直位移,σ和s分别是根据晶格和自旋定义的泡利矩阵.考虑到整个布里渊区的热平均,这个声子振动会导出一个局域项HKM=Δ(r)σzsz,其中Δ(r)是弯曲声子对于Kane-Mele耦合的贡献,它正比于〈h2〉.所以,石墨烯狄拉克点附近的电子低能量的等效哈密顿模型为(3)式KM 型的有效哈密顿量可以解释本实验中出现的KM 型自旋-轨道相互作用.

由此模型可合理地预见,自旋的z分量守恒.石墨烯中只有面内的自旋有可能在散射过程中经历翻转.Δ(r) 可按照由高斯型δ函数表示的无序来处理,即其中∫表示无序关联的强度.无序系统配分函数式中D是泛函积分;ψ是费米子产生算符;S=S0+S1,其中S0是无质量狄拉克费米子项,S1是无序项,

我们假设S1是很小的能量修正,进行微扰展开.之后通过无序平均[33]的处理,得到

式中S=S0+S′,其中,

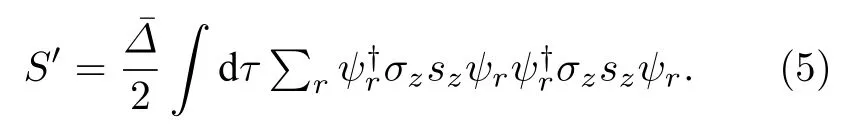
以平均场的方法处理得到

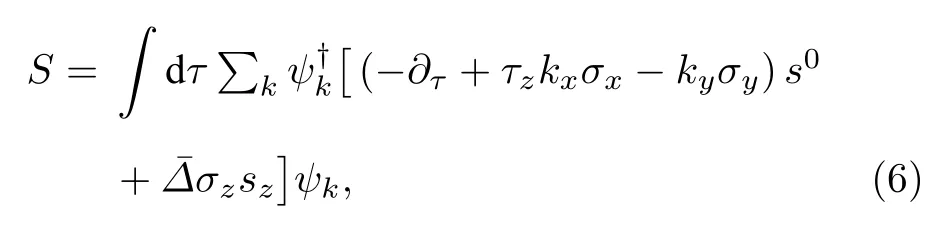
式中,第一项描述的是本征石墨烯电子在动量空间狄拉克点附近的展开;第二项是修饰后的石墨烯随机矢量势场诱导的类似KM 型的自旋-轨道耦合,其耦合强度正比于这样,就出现了一个全局的等效的KM 型自旋-轨道耦合.由(3)式这个等效哈密顿量对应的薛定谔方程,可以得到自旋翻转的概率为符合EY 型自旋弛豫机制.

4 结论

修饰石墨烯可能会引入可观的Rashba 型自旋-轨道相互作用,而通过EDTA-Dy 分子修饰石墨烯可能选择性地增强了KM 型的自旋-轨道相互作用,本文研究发现其受抑制的弱局域化效应证明了这一点.同时石墨烯的量子输运性能得到了提高,其狄拉克费米子的量子霍尔效应得以实现.石墨烯修饰后造成的界面拉伸和局域的涟漪导致了内禀自旋-轨道相互作用的增强和量子输运性能的提高,并以此提出了自旋-弯曲声子耦合的模型.希望本实验能够推进石墨烯中拓扑态的研究.