丝驱动蛇形臂机器人的被动柔顺特性分析
2022-03-30刘北尹来容黄龙胡波
刘北,尹来容,黄龙*,,胡波,2
(1. 长沙理工大学 汽车与机械工程学院,长沙 410114; 2. 长沙理工大学 机械装备高性能智能制造关键技术重点实验室,长沙 410114)
蛇形臂机器人具有结构紧凑、运动灵活等特点,近年来在复杂环境下的维修与救援[1-3]与医疗手术[4]等领域得到了广泛应用。国内外学者相继设计了构型各异的蛇形臂机器人样机,驱动方式主要包括丝驱动、气动肌肉驱动、形状记忆合金弯曲变形等。其中,丝驱动方式因具有占用空间小、可使质量较大的驱动器远离末端执行机构等优势,在蛇形臂机器人应用更为广泛。
Li等[5-6]提出了一种由多个球关节和柔性骨架组成的丝驱动蛇形臂机器人,通过这种设计使得蛇形臂机器人结构更紧凑。基于刚性定轴转动关节,Shen等[7]设计了一种可用于经自然腔道内镜手术的丝驱动蛇形臂机器人。熊志林等[8]利用丝驱动设计了一种具有万向节结构的蛇形臂机器人,并结合关节结构的物理限制改进了末端跟随运动。杨文龙等[9]中基于柔性切口结构提出一种丝驱动的平面连续体机械臂,并建立了针对该切口结构的机械臂力学模型。王海等[10]给出了一种具有六自由度柔性关节的机械臂简化模型,并基于拉格朗日方法对其动力学进行了分析。Yoon等[11-12]以弹簧作为柔性关节建立了一种含有四自由度的丝驱动蛇形臂机器人,并应用于微创外科手术中。但大多含有刚性转动关节或柔性关节的丝驱动蛇形臂机器人当其末端受到外部横向力作用时,在关节内的丝仍有可能会松弛,从而导致蛇形臂机器人构型不可控,这种特性即为被动柔顺特性[13]。
为避免被动柔顺特性,Zhang等[14]利用等腰梯形机构研制了一种可用于手术器械的蛇形臂机器人可重构单元。基于柔性关节,Dong等[15-16]提出了一系列丝驱动蛇形臂机器人设计,且在其末端受到外部干扰时能防止丝的松弛。Suh等[17-18]与Kim等[13]均提出了一种由柱面滚动关节串联构成的可避免被动柔顺特性的丝驱动蛇形臂机器人,但并没有深入探讨被动柔顺特性的本质。但关节结构的不同会导致相应丝驱动蛇形臂机器人的构型稳定性及其避免被动柔顺特性的能力存在一定差异。
首先总结丝驱动蛇形臂机器人的关节类型与结构特点。以含有定轴转动关节的典型丝驱动蛇形臂机器人为例,分析被动柔顺特性的产生机理,并提出一种被动柔顺指标。基于关节运动学建立关节结构参数与被动柔顺指标之间的关系,得到可避免被动柔顺的关节结构参数设计要求,并在此基础上,构建不同类型的丝驱动蛇形臂机器人构节。
1 蛇形臂机器人的关节类型
丝驱动蛇形臂机器人的关节类型多样,典型的关节包括刚性转动关节、柔性关节、柱面/球面滚动关节,其关节自由度可分为单自由度或多自由度。常见的单自由度关节包括单自由度定轴转动关节、柔性板簧和柱面滚动关节(图1a)),而常见的多自由度关节包括虎克铰/球关节、柔性中心杆和球面滚动关节(图1b))。在实际的结构限制下,蛇形臂机器人的关节扭转自由度通常受到约束,因此实际只能实现两自由度运动。由两自由度关节构成的蛇形臂机器人可在一定程度上提升蛇形臂机器人的弯曲变形幅度,但其运动控制难度也相对较大。相比而言,单自由度关节在蛇形臂机器人中应用更为广泛,但若要构成两自由度构节,需要在关节叠加过程中,使相邻关节的瞬时转轴保持异面垂直。
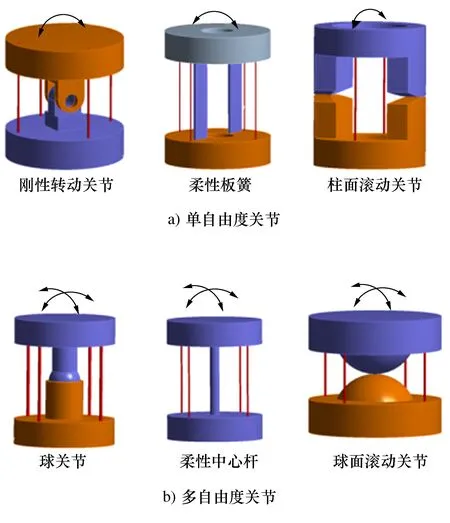
图1 典型的单自由度关节与多自由度关节
本文选取3种典型的基于单自由度关节的蛇形臂机器人作为研究对象分析其结构特点。蛇形臂机器人通常由多个构节串联构成[19],每个构节又由若干个相同的关节串联而成,可实现两自由度弯曲变形。多个两自由度构节的串联之后,可以实现整体的复杂弯曲构型,以适应更复杂的环境。如图2所示,丝驱动蛇形臂机器人单个构节的基本构型都由一个基座盘、多个间隔盘、一个末端盘和沿周向均匀布置的多条丝组成。相邻间隔盘之间通过刚性铰链、柔性杆或柱面/球面滚动副连接,进而形成了一个关节。每条丝的一端与末端盘固连,另一端固连在驱动轮上。此外,对径位置也可以采用一整条丝,即丝的两端均固定在末端盘上,而在其中间位置绕过驱动轮。通过驱动轮的转动使得相应的各条丝拉紧和释放,进而使得构节发生弯曲变形。与传统机器人相比,丝驱动蛇形臂机器人的所有驱动电机不是安装在每个关节中,而是安装在一个驱动系统中。该驱动系统一般位于蛇形臂机器人首个构节中第一个关节附近。由于构节中的关节数量通常显著大于电机数量,整个构节具有欠驱动特性。
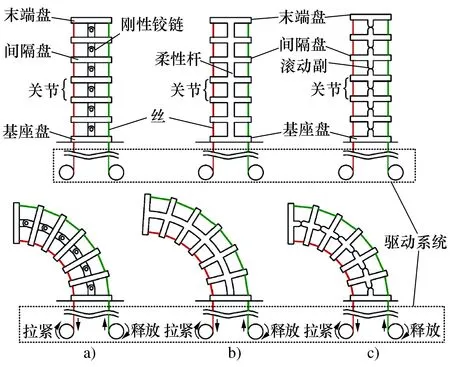
图2 丝驱动蛇形臂机器人构节的理想状态
2 丝驱动蛇形臂机器人的被动柔顺
在对丝驱动蛇形臂机器人进行运动学建模的过程中,通常假设机器人始终保持理想构型,即在直线构型下保持所有间隔盘相互平行,不产生局部弯曲(图3a)),而在弯曲构型下,每个关节的转角保持相等(图3b))。然而由于构节的欠驱动特性与丝驱动的单侧约束特性,理想构型假设并不是始终成立的,大多现有的蛇形臂机器人在微小外界扰动下会大幅度偏离理想构型,例如由理想直线构型(图3a))变为S构型(图3c)),即被动柔顺特性。

图3 被动柔顺特性
为了便于讨论,不妨将各丝的释放/拉紧量作为机器人的输入,而各关节的弯曲角度和弯曲方向(即机器人构型)作为机器人的输出。在张紧状态下,机器人输入与构节中各丝长度(Ll与Lr)一一对应;而松弛状态下则不存在一一对应关系。当机器人处于初始直线构型时(图3a)),在构节中所包含的左右两侧丝的长度相等(Ll=Lr)。若在合适的输入下,无外力作用的构节可实现理想的均匀弯曲构型(图3b)),此时Ll减少为L′l,Lr增加为L′r。然而无论是初始直线构型,还是均匀弯曲构型,能否在扰动下保持稳定,与关节类型和关节参数密切相关。以图3a)所示的刚性转动关节构成的构节为例,通过简单的几何推导可知,当其弯曲时,在单个关节中有l′l1+l′r1<2ll0=2lr0,整理可得Δll+Δlr<0,即关节内的左右两侧丝长度变化量的代数和为负值。
进一步考虑构节的两种构型状态,即直线构型(图3a))与S构型(图3c)),其中S构型由两段均匀弯曲部分反向叠加而成,且左右两侧丝的长度在S构型下满足
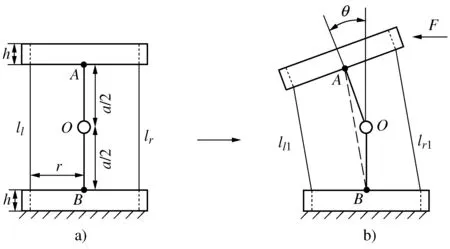
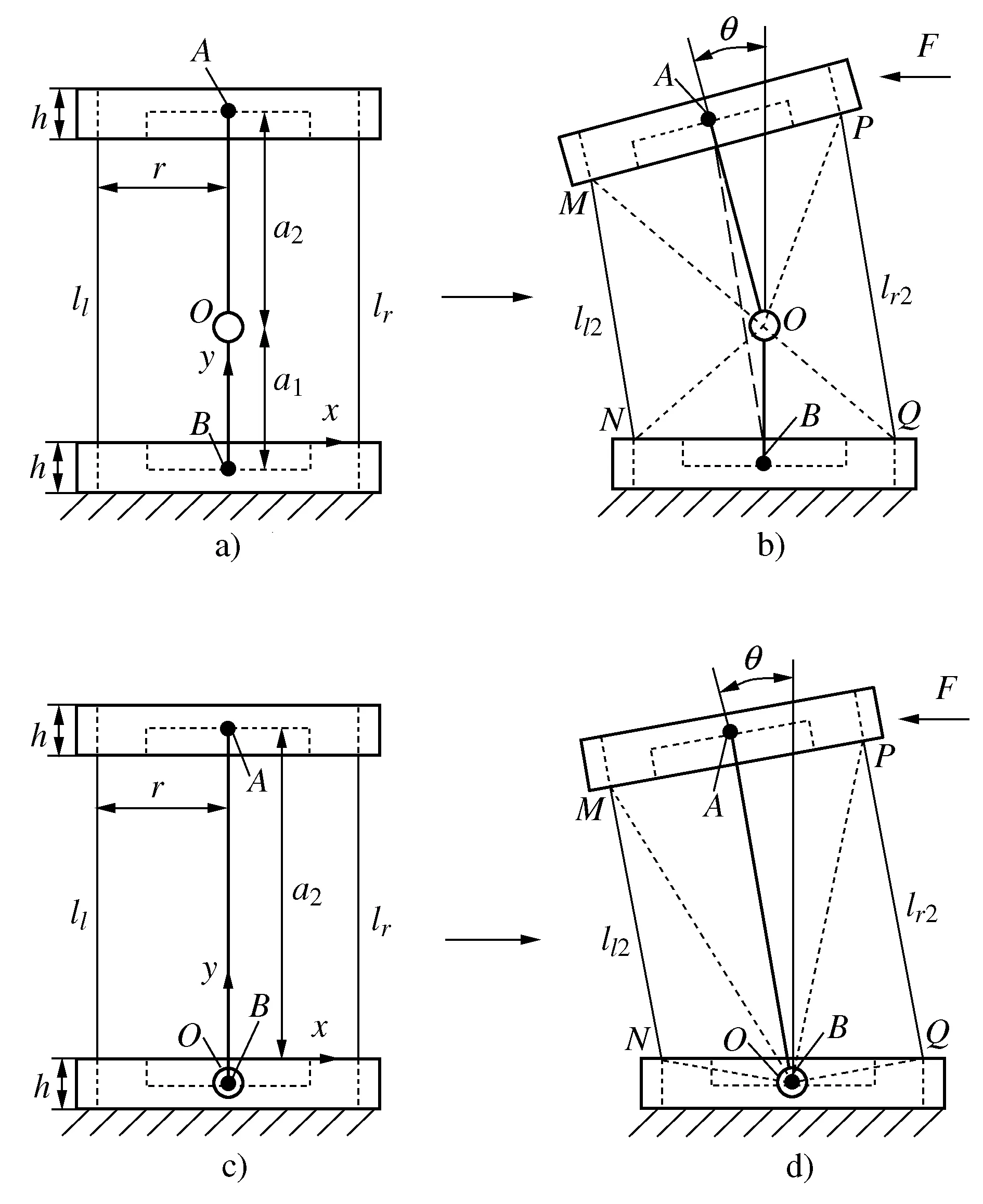
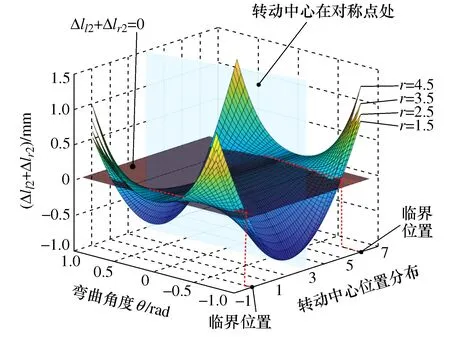
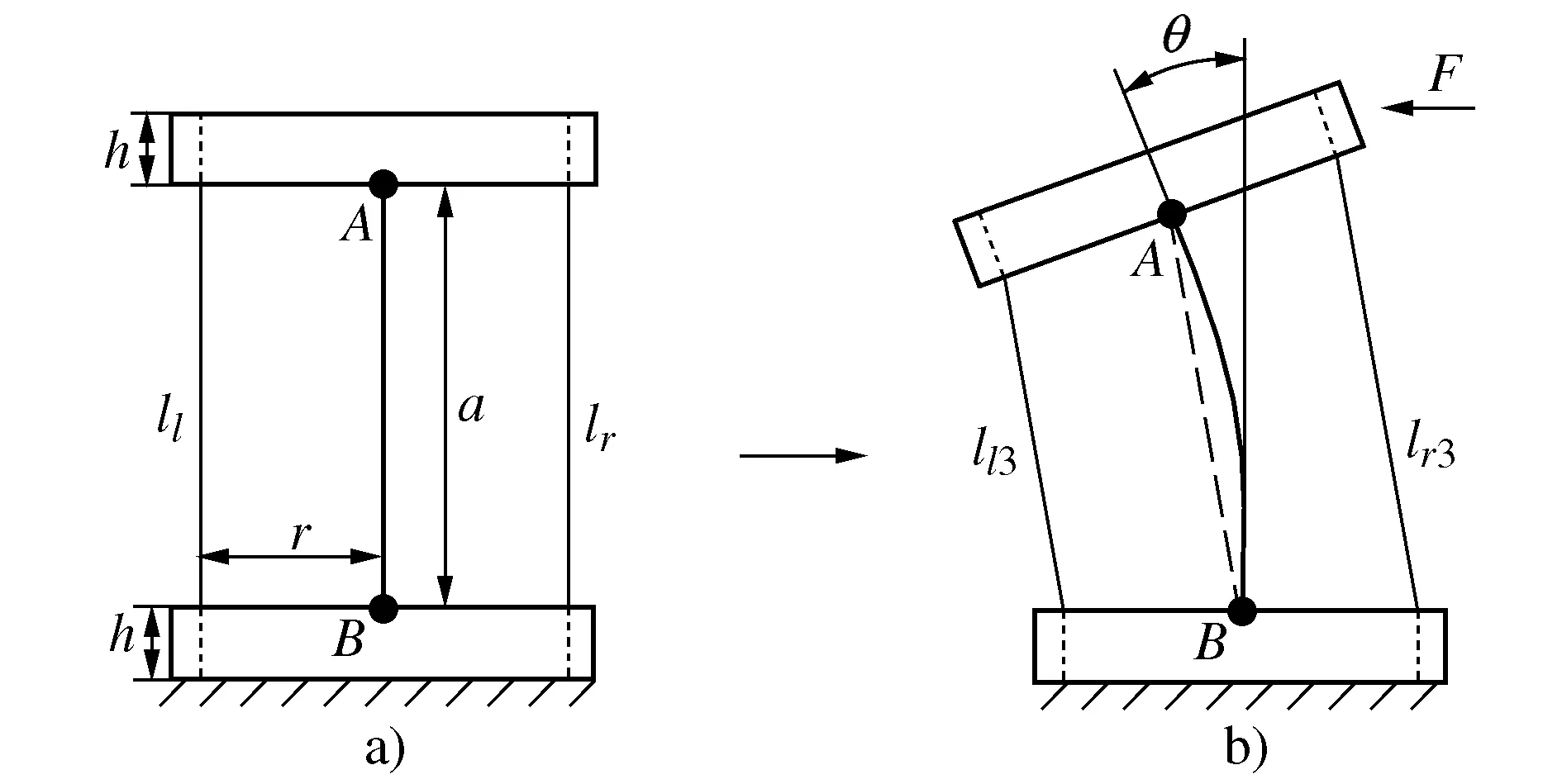
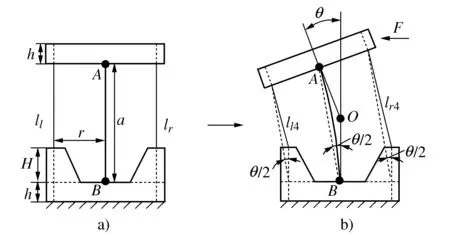
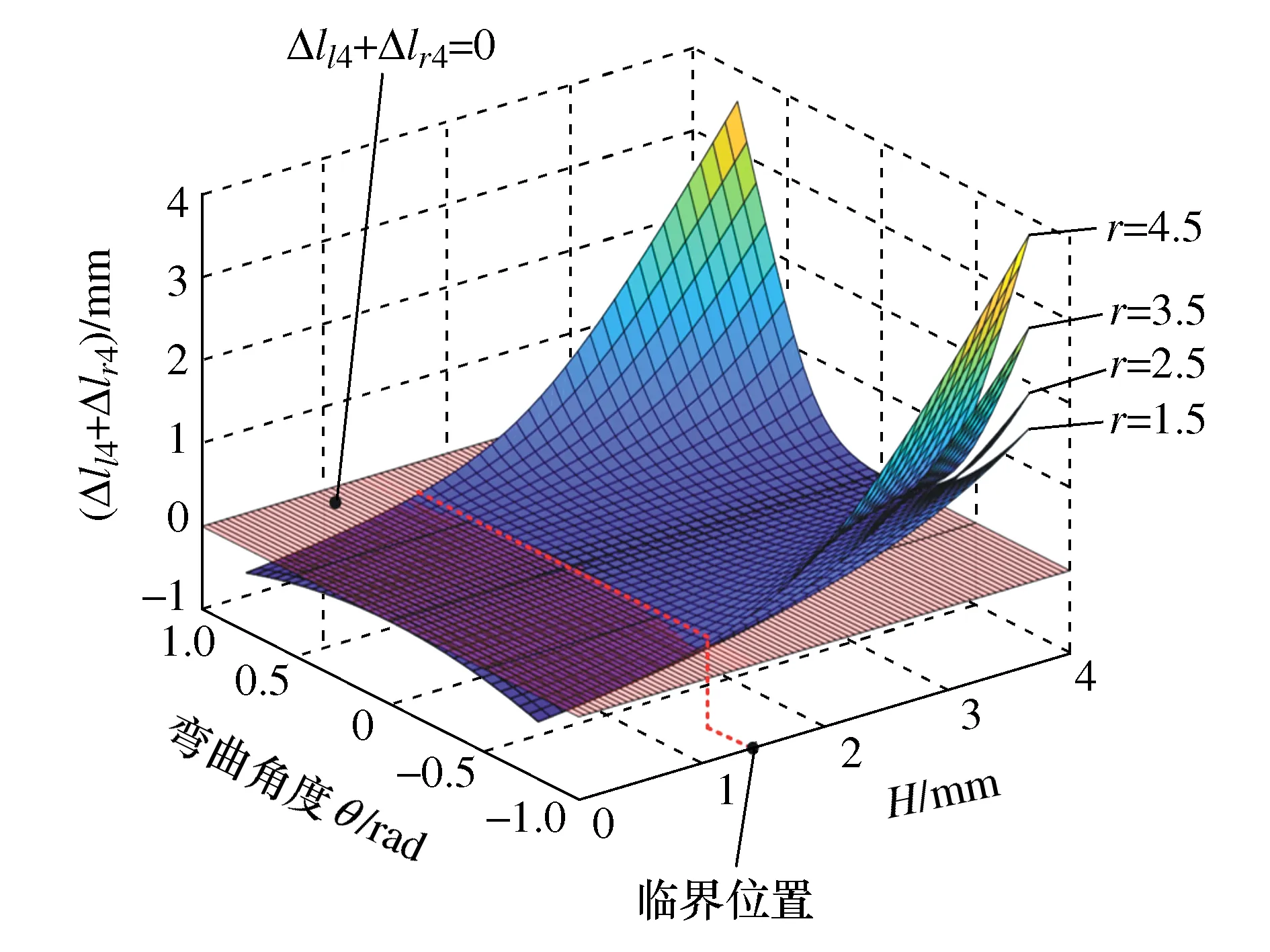
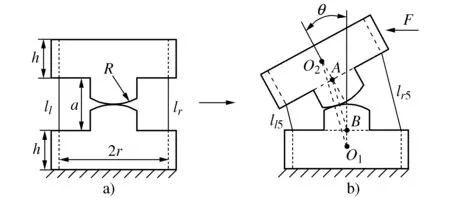
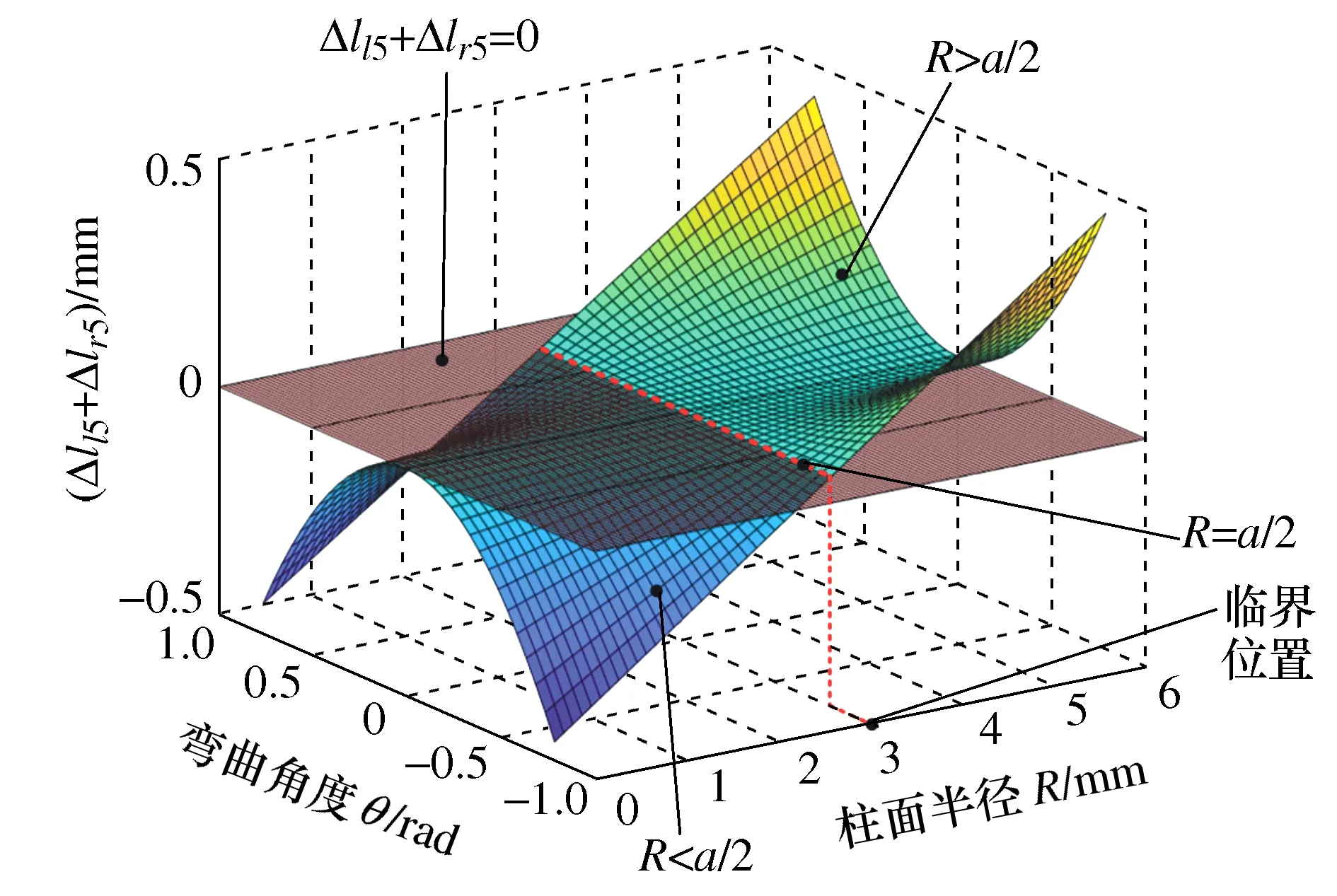
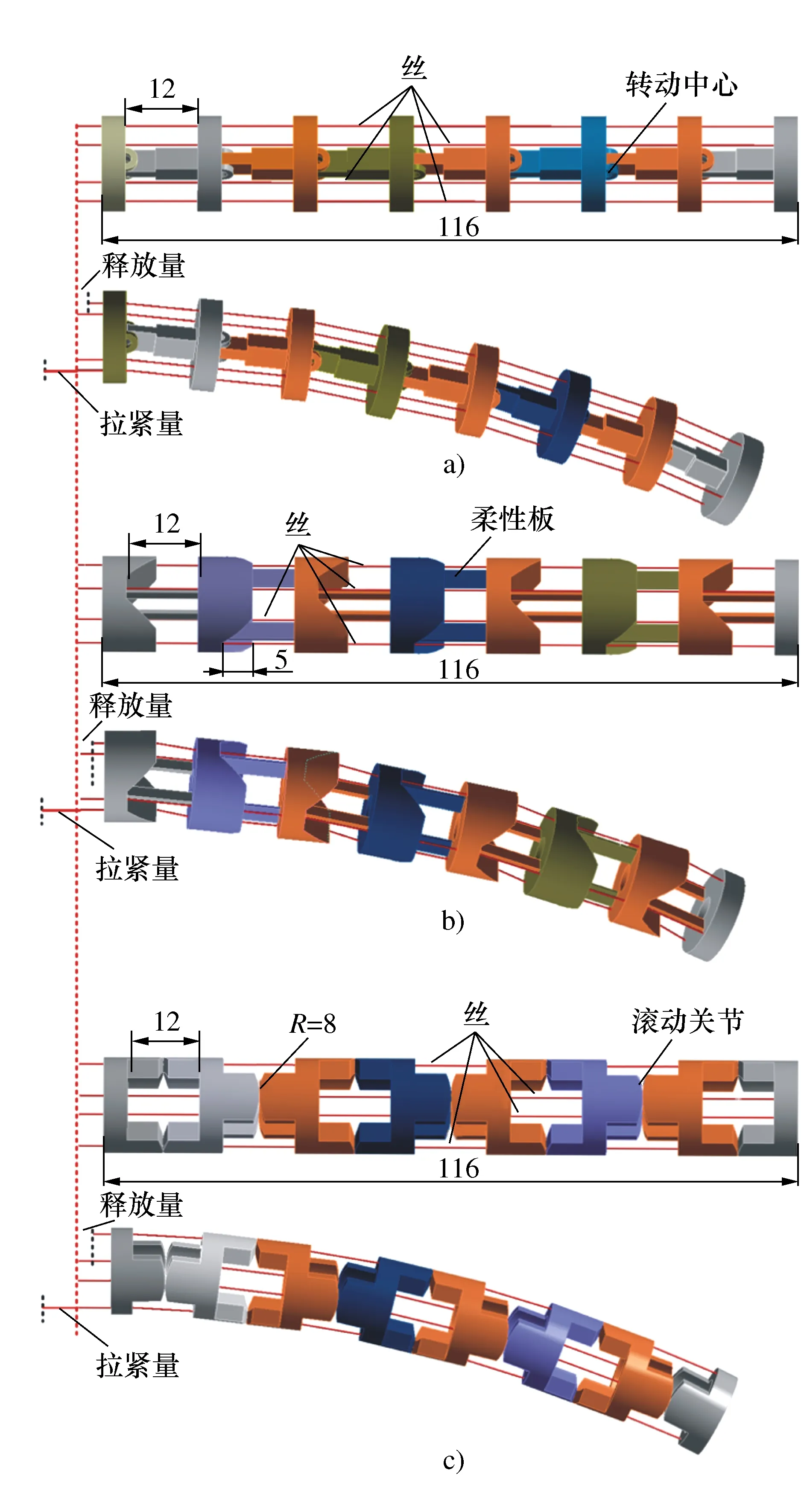
L″l1+L″l2=L″l=L″r=L″r1+L″r2 (1) 此时构节中的左右两侧丝长度均比直线构型下更短,因此在驱动输入保持不变时两侧丝均会松弛。正是由于这种特性,丝驱动蛇形臂机器人的同一个输入对应于多个构型输出,这将导致机器人构型不可控。 若在其单个关节中左右两侧丝的长度变化量的代数和满足Δll+Δlr>0,则左右两侧丝的长度在相应构节的S构型下满足 L″l1+L″l2=L″l=L″r=L″r1+L″r2>Ll=Lr (2) 此时构节中两侧丝的长度均比直线构型时更长,因此,在输入不变的情况下,构节不可能由直线构型变为S构型甚至任意其它构型,因此能够保持其构型稳定性,可避免具有被动柔顺特性。 根据上述推导,本文以Δll+Δlr为被动柔顺指标,具体分析3种单自由度关节的结构参数与丝驱动蛇形臂机器人中被动柔顺特性的关系。 基于3种单自由度关节,本节分别推导了其关节参数、弯曲角度与被动柔顺指标之间的关系,进而分析出关节结构参数对被动柔顺特性的影响,总结出避免被动柔顺特性的结构参数设计要求。为便于分析,作以下假设:1) 在3种单自由关节内两对丝周向均匀分布,其中一对丝在该关节的弯曲平面内用于驱动该关节弯曲,同时在该关节内的另一对丝的长度保持不变;2) 丝与丝孔之间不存在间隙,且丝的抗拉刚度为无穷大;3) 当关节末端受到外力作用时,机器人的输入保持不变。3种关节的基本结构参数定义如下:r为丝分布圆半径;a为关节初始间隙(柔性关节长度);h为间隔盘厚度;R为柱面/球面半径;ll,lr表示在3种关节内左右两侧丝的初始长度;lli,lri(i=1,2,3,4,5)表示3种关节受到外部横向力时左右两侧丝的弯曲长度;Δlli,Δlri表示在3种关节中左右两侧丝在受力弯曲前后的变化量。 定轴转动关节包括关于转动中心O的上下对称和非对称两种情形。如图4所示的转动关节为对称情形,即转动中心与关节初始间隙的中间位置。在初始状态下(图4a)),则左右两侧丝的长度ll=lr=a+2h。在一定的外部横向力F作用在该转动关节的末端时,假设该转动关节绕转动中心O转动θ角度(图4b)),左侧的丝长ll减少到ll1,右侧的丝长lr增加到lr1。 图4 对称情形的定轴转动关节 根据几何结构可知,线段AB表示相邻间隔盘的中心线,其长度为 (3) 在该关节受到外部横向力F时,其左右两侧丝长分别为: (4) 因此初始状态与受力弯曲状态相比,关节内的两侧丝的变化量为: (5) 由式(5)可知Δll1+Δlr1=2a(cos(θ/2)-1)<0。这表明在定轴转动关节的对称情形下,丝在外部横向力作用时可能出现松弛现象,因此由该关节构成的丝驱动蛇形臂机器人具有被动柔顺特性。 假设在定轴转动关节的非对称情形下(图5),转动中心O到下间隔盘的上边缘距离为a1,到上间隔盘的下边缘距离为a2,且上下间隔盘的边缘距离为a。在初始状态时左右两侧丝的长度ll=lr=a+2h。 图5 非对称情形的定轴转动关节 若在一定的外部横向力F作用在该转动关节末端时,该转动关节绕转动中心O转动了θ角度,左侧的丝长ll减少到ll2,右侧的丝长lr增加到lr2,且转动中心在关节内任意位置时,在OMN和OPQ中均满足: (6) 但∠MON和∠POQ随着转动中心位置的变化而变化。如图5a)和5b)所示,当转动中心O在上间隔盘和下间隔盘的中间任意位置时二者分别满足: (7) 如图5c)和5d)所示,当转动中心O在下间隔盘的内部任意位置时∠MON和∠POQ分别满足: (8) 类似地,当转动中心O在上间隔盘的内部任意位置时∠MON和∠POQ分别满足: (9) 根据余弦定理,关节内的左右两侧丝在受到外部横向力时的长度为: (10) 因此,其左右两侧丝变化量为: (11) 假设初始间隙为a=6 mm,转动中心位置分布区间为[-1,7],丝分布圆半径r分别取1.5 mm,2.5 mm,3.5 mm和4.5 mm。当弯曲角度θ的范围为[-π/4,π/4]时,Δll2+Δlr2与转动中心位置分布、丝的分布圆半径之间的关系如图6所示。 图6 定轴转动关节参数对Δll2+Δlr2的影响 当转动中心处于对称点(a1=a2=3)时,Δll2+Δlr2始终小于零,且随着弯曲角度的增大而减小。在非对称情形下,Δll2+Δlr2随转动中心与对称点之间的距离增大而增大,且在上间隔盘的下边缘处和下间隔盘的上边缘处为Δll2+Δlr2大于零的临界位置。Δll2+Δlr2随着丝分布圆半径r的增大而增大。这表明对于定轴转动关节的丝驱动蛇形臂机器人,存在合理的丝分布圆半径及转动中心位置,使得Δll2+Δlr2>0成立,且不具有被动柔顺特性。 与定轴转动关节类似,柔性关节也可分为两种情形:关于弯曲中心的上下对称情形和非对称情形。目前,对具有柔性关节的丝驱动蛇形臂机器人研究通常采用分段常曲率假设模型[20-21]。在上下对称情形的初始状态下(图7a)),其关节内的左右两侧丝长度ll=lr=a+2h。 图7 含有柔性关节的对称情形 如图7b)所示,假设在外部横向力F作用在该转动关节的末端时柔性关节以常曲率k均匀弯曲θ角,则间隔盘的中心线AB长度可知 (12) 此时,该关节内的左右两侧丝长度为: (13) 因此该柔性关节初始状态与受力弯曲状态相比,其左右两侧丝的变化量为: (14) 在实际工作中,丝驱动蛇形臂机器人的各转动关节弯曲角度一般小于45°,因此有 (15) 这表明当有外部横向力的作用时,丝会出现松弛现象。因此由该柔性关节构成的丝驱动蛇形臂机器人具有被动柔顺特性。 在上下非对称情形的柔性关节内(图8),上间隔盘约束的丝长度为h,下间隔盘约束的丝长度为H+h,柔性关节的长度为a。在初始状态下左右两侧丝长ll=lr=a+2h。 图8 非对称情形的柔性关节 当存在外部横向力F作用在该柔性关节末端时(图8b)),左右两侧丝长为: (16) 因此该柔性关节的初始状态与弯曲状态相比,两侧丝的变化量分别为: (17) 由式(17)可知:假设初始间隙为a=6 mm,H∈[0,4],丝分布圆直径r分别取1.5 mm,2.5 mm,3.5 mm和4.5 mm。在弯曲角度范围为[-π/4,π/4]时,丝分布圆半径、间隔盘凸起厚度H及弯曲角度等基本关节结构参数与Δll4+Δlr4的关系如图9所示。 图9 柔性关节参数对Δll4+Δlr4的影响 当H大于图9所示的临界位置时,不等式Δll4+Δlr4>0一定成立。Δll4+Δlr4随着丝分布圆半径r的增大而增大。这表明在非对称情形下,通过合理设计关节结构参数可避免其具有被动柔顺特性。随着H的增大,丝驱动蛇形臂机器人柔性转动关节的弯曲范围会受限。 在初始状态下(图10a)),左右两侧丝的长度ll=lr=a+2h。假设当一定的外部横向力F作用在滚动关节末端时,其关节上模块相对其下模块沿圆柱面滚动θ角度(图10b)),左侧的丝长ll减少到ll5,右侧的丝长lr增加到lr5。 图10 柱面滚动关节 根据图10b)所示的几何结构可知,AB//O1O2,AO1=BO2=R-a/2,线段O1O2表示相邻两圆柱面的圆心连线且其长度等于2R,线段AB可看作为间隔盘上的丝分布圆的圆心连线,且其长度为 (18) 此时在柱面滚动关节内的左右两侧丝长为: (19) 因此,初始状态与弯曲状态相比两侧丝的变化量分别为: (20) 根据式(18)可知,Δll5+Δlr5与丝分布圆半径无关。假设初始间隙为6 mm,弯曲角度范围为[-π/4,π/4]时,Δll5+Δlr5与弯曲角度、柱面半径R及初始间隙之间的关系如图11所示。 图11 柱面滚动关节参数对Δll5+Δlr5的影响 若R=a/2,无论弯曲角度取何值,Δll5+Δlr5=0均成立且(Δll5<0,Δlr5>0),此时不具有被动柔顺特性;若R>a/2,则Δll5+Δlr5>0,且Δll5+Δlr5随弯曲角度增大而增大,此时不具有被动柔顺特性;若R 如图12所示,本节通过采用多个关节模块正交排列的方式分别设计了3种不具有被动柔顺特性的两自由度弯曲丝驱动蛇形臂机器人构节。 图12 3种蛇形臂机器人构节 如图12a)所示的具有定轴转动关节的蛇形臂机器人构节,其关节数量为7个,关节初始间隙a=12 mm,间隔盘的厚度h=4 mm,转动中心到下间隔盘的距离为0,到上间隔盘的距离为12 mm;如图12b)所示的具有柔性关节的蛇形臂机器人构节,其关节数量为7个,关节初始间隙a=12 mm,间隔盘厚度h=4 mm和凸起厚度H=5 mm,柔性板参数为1 mm×1.5 mm×12 mm;如图12c)所示的具有柱面滚动关节的蛇形臂机器人构节,其关节数量为7个,关节初始间隙a=12 mm,柱面半径为8 mm,间隔盘厚度为h=4 mm。上述3种丝驱动蛇形臂机器人构节的各个关节模块均采用铝合金材质,其每个关节直径为8 mm,构节总长度为116 mm,其中丝为直径0.5 mm的不锈钢丝,丝分布圆半径r=3.5 mm。 如图12和图13所示,当3种丝驱动蛇形臂机器人构节在无外力作用下的单自由度弯曲时,丝的释放量小于拉紧量。即随着弯曲角度的增大,在构节内的两侧丝变化量的代数和始终大于零(即Δll+Δlr>0)。这表明所建立的3种丝驱动蛇形臂机器人构节在输入保持不变时,能够避免被动柔顺特性。 图13 弯曲角度对Δll+Δlr的影响 1) 对于具有定轴转动关节和柔性关节的丝驱动蛇形臂机器人,在关节上下对称情形时无法避免被动柔顺特性,在关节上下非对称情形时均可以通过合理设计关节的结构参数避免被动柔顺特性。 2) 对于具有柱面滚动关节的丝驱动蛇形臂机器人,则要求柱面的半径明显大于关节初始间隙的一半。 3) 给出了3种能避免被动柔顺的丝驱动蛇形臂机器人构节的设计实例。3 结构参数对被动柔顺特性的影响
3.1 定轴转动关节
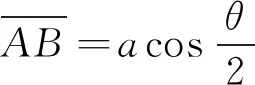
3.2 柔性关节
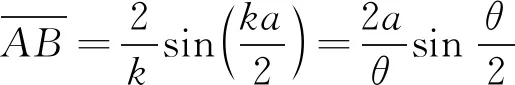
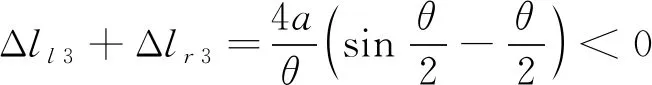

3.3 柱面滚动关节
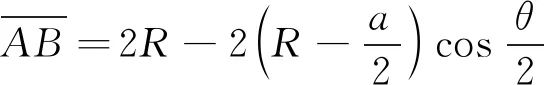
4 设计实例

5 结论
