CQTBEW算法及其在轴承早期故障诊断中的应用
2022-03-30邹金玉王太勇王鹏
邹金玉,王太勇,王鹏
(天津大学 机械工程学院,天津 300354)
滚动轴承作为旋转机械设备的关键零部件之一,其故障状态尤其是早期故障的监测与诊断具有十分重要的意义。轴承发生故障时,损伤部位会与其它表面碰撞产生冲击能量信号,对故障信号的诊断通常采用振动信号分析法,通过传感器采集设备关键部位的振动信号,进行时域、频域或者时频域分析,提取相应的故障特征[1-2]。由于滚动轴承的振动信号通常为非线性的动态信号,时频域分析方法应用最为广泛[3]。典型的时频分析方法如短时傅里叶变换、小波分析、Wigner-Ville分布等有着很好的应用[4-6]。但均存在着问题,短时傅里叶不适用于非平稳信号、小波分析基函数选择困难、Wigner分布存在交叉性问题。对于以上不足,经验模态分解、局部均值分解、变模态分解等具有自适应特性的算法被提出。这些算法对非平稳振动信号的诊断分析效果较好[7-9]。对于强噪声环境下轴承故障特征的提取,常用的方法是先对信号进行降噪处理,提高信号的信噪比,再进行进一步的分析,如EMD降噪和谱峭度法、二代小波去噪和形态滤波法、连续小波变换等[10-12]。在降噪过程中会存在着故障信号被削弱的问题,非线性随机共振方法将部分噪声能量转化为信号能量,一定程度上可增强微弱特征[13]。王鹏[14]提出二值化能量权重算法,对时频谱进行局部极值二值化处理,将振动信号转化为能量权重时间序列,对微弱故障信号起到了很好的增强作用。
恒Q变换作为一种时频变换方法,具有时频窗口自动调节的优点,高频信号时域分辨率高,低频信号频率分辨率高,可以获得频率轴指数分布的时频谱[15]。本文将恒Q变换得到的时频谱进行二值化能量增强处理,提出一种恒Q变换时频谱二值化能量增强算法(CQTBEW)。
1 CQTBEW算法
CQTBEW算法实现过程算法主要包括时频谱获取与时频谱增强处理两部分,其具体实现过程分为以下4个步骤:
步骤1 将采集到的故障轴承振动加速度信号进行恒Q变换(CQT),获得CQT时频谱;
步骤2 对CQT时频谱图进行频率段划分,分别进行多尺度下的二值化时频谱增强,获得不同尺度的二值化能量谱;
步骤3 将不同尺度的二值化能量谱进行时间轴方向求和,获得多尺度能量时间序列,然后将多个能量时间序列再次叠加求和,得到集合能量时间序列;
步骤4 最后对集合能量时间序列进行功率谱分析获得特征频率。CQTBEW算法流程如图1所示。

图1 CQTBEW算法流程图
1.1 恒Q变换
1991年,Brown[16]提出了恒Q变换,这种方法与离散傅里叶变换相似,可以将时域信号转换至时频域进行分析。恒Q变换与离散傅里叶变换的不同之处在于,它变换得到的频域点间隔是呈指数规律的,而离散傅里叶变换的频率点间隔是相同的。
从滤波器的角度分析,DFT是中心频率等间隔分布,带宽相同的滤波器组,CQT是中心频率与带宽的比为定值Q的滤波器组。CQT的时频域窗口是可调整的,一般对快变信号,它有较高的时域分辨率,较低的频域分辨率;对于慢变信号,有较低的时间分辨率,较高的频率分辨率。恒Q变换实现公式为
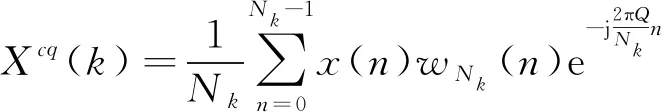
(1)
式中:wNk(n)是长度为Nk的窗函数;Q是CQT变换中的常数因子;k是CQT谱的频率序号;Nk为窗口样本数,和k值有关。
中心频率fk、常数Q因子、窗口长度定义为:
fk=f0*bk
(2)
Q=fk/Δf
(3)
Nk=Qfs/fk
(4)
式中:f0为最小频率;b为相邻频率的倍率;Δf为频率间隔;fs为采样频率。
1.2 二值化能量权重法
实际生产通常伴随有很多噪声信号,对强噪声环境下采集到的微弱冲击信号进行传统的时频分析时,往往很难发现明显的突变点,即冲击信号被噪声淹没。为了实现对能量时间序列中冲击成分的增强,通过使用多种与典型故障特征频率相关的窗口进行冲击识别,从而实现能量时间序列的多尺度二值化,进而实现时频谱的多尺度二值化,得到不同尺度特征下的二进制谱。其具体实现方法如下:
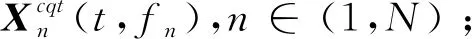

步骤3 多次进行步骤2,对整个时频谱所有频率段的时间序列进行二值化处理,获得大小与时频谱矩阵Xcqt(t,f)相同的能量增强矩阵brzXcqt(t,f);
步骤4 选取d值不同的窗口长度进行处理,重复步骤2和步骤3,获得不同尺度下的能量增强矩阵。
其中,滑动窗口长度的选取原则为:首次计算的窗口长度应在故障的两次冲击时间与3次冲击时间之间。

(5)
将不同尺度的能量时间序列进行叠加,获得集合能量时间序列,实现公式为

(6)
式中M为获得的能量时间序列个数,即采用不同尺度的数量,取M=6。
最后对集合能量时间序列进行功率谱密度分析,将功率谱分析得到的明显频率成分与故障特征频率进行对比,确定故障位置。

(7)
式中:F[grbrzx(t)]为集合能量时间序列的傅里叶变换;T为样本时间。
2 仿真分析与验证
仿真一种强噪声环境下的轴承故障冲击信号对本方法进行分析验证,仿真信号特征频率设定为25 Hz。仿真冲击信号x(t)与时间t的函数关系式为
(8)
其中设定采样频率为5 120 Hz,幅值衰减系数g为0.5,采样时间为20 s,仿真冲击信号如图2所示。

图2 25 Hz的仿真冲击信号
为了更加真实地模拟强噪声环境下的振动信号,在仿真冲击信号中添加了较强能量成分的噪声,其信噪比SNR为-23,添加白噪声后的冲击信号如图3所示。

图3 加入白噪声后的仿真信号
针对此仿真信号采用包络谱频谱分析,得到结果图如4所示。从图4中已经无法明显看到特征频率的基频以及二倍频成分,25 Hz的冲击信号被噪声淹没而无法检测出来。

图4 仿真信号包络谱
对添加白噪声后的仿真冲击信号X(t)进行CQTBEW分析处理。首先,对信号进行恒Q变换获得时频特征图,如图5所示;其次,将时频图划分为不同的频率段进行二值化增强处理,获得了6种不同的尺度下的时频图二值化增强图,如图6所示;再次,将6种尺度下的二值增强图谱向时间轴方向进行求和叠加,获得对应的能量增强时间序列,如图7所示;最后,将各个能量时间序列进行求和,获得集合能量增强时间序列,如图8所示。

图5 仿真信号时频图

图6 多尺度时频图二值增强图

图7 仿真信号能量增强时间序列

图8 仿真信号集合能量增强时间序列
对仿真信号的集合能量增强时间序列做功率谱分析,结果如图9所示。从功率谱可以明显地看到25 Hz的特征频率成分,说明CQTBEW算法对较强噪声环境下的冲击信号分析是有较好效果的。

图9 仿真信号集合能量增强时间序列功率谱
3 试验分析与验证
本文的试验数据来源于铁科院机车车辆研究所自行设计制造的JT-301型轮对实验台。该试验台整体由驱动电机、托举装置、支撑装置等部分组成,实验中使用的滚动轴承型号为352226x2-2z,该型号轴承参数如表1所示。

表1 352226x2-2z轴承参数表
试验中的轴承状态主要有3种:无明显故障、外圈故障、内圈故障。本文试验选用外圈故障轴承的振动加速度信号进行分析验证,采样频率为5 120 Hz,样本时间为10 s,外圈故障频率为67.55 Hz,转速为469 r/min。振动加速度随时间变化的图像如图10所示。

图10 振动加速度信号时域图
对上述振动加速度信号进行包络谱频谱分析,可以得到如图11所示的分析结果。分析包络谱频谱,可以发现在特征频率的二倍频处出现了较大的幅值,这说明上述测得的振动加速度信号确实为存在故障的振动信号。但是在包络谱中无法观察到基频成分,说明在较强的噪声环境中,故障轴承的特征频率信号成分被淹没。

图11 故障信号包络谱
将故障振动信号进行CQTBEW分析,先对振动加速度信号做恒Q变换获得时频谱,如图12所示,对获得的时频变换矩阵进行频率段划分获得对应的能量时间序列。其次对各频率段的能量时间序列进行二值化能量增强处理,选择不同尺度的能量增强窗口分别对能量时间序列进行处理获得不同尺度下的能量增强二进制谱。试验中进行了6次不同尺度下的二值化处理,其对应的窗口长度分别为L1=105,L2=209,L3=417,L4=833,L5=1 665,L6=3 329,不同尺度下的二进制强化谱如图13所示。

图12 恒Q变换时频图
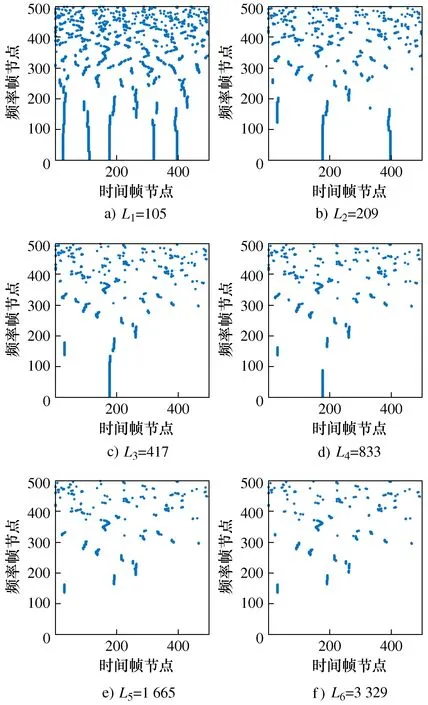
图13 多尺度试验时频图二值增强图
对上一步获得的多尺度二值化增强图谱值向时间轴方向叠加,得到多尺度二值化能量增强时间序列BEETS1、BEETS2、BEETS3、BEETS4、BEETS5、BEETS6,如图14所示。将不同尺度下的二值化能量增强时间序列叠加,得到集合二值化能量增强时间序列setBEETS,如图15所示。
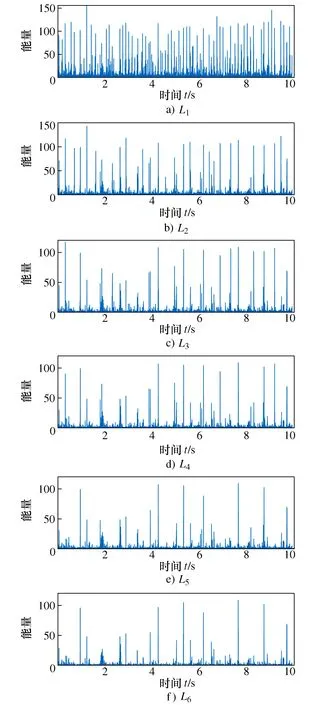
图14 多尺度二值化能量增强时间序列

图15 集合二值化能量增强时间序列
最后对集合二值化能量增强时间序列做功率谱分析,结果如图16所示。从功率谱可以明显频率67.5 Hz以及其二倍频处频率成分,通过与故障特征频率进行对比可以确定该故障为外圈故障。CQTBEW分析的结果表明,此算法可以对强噪声环境下的轴承故障进行诊断分析,通过对故障频率的分析以确定故障位置,是比较有效的,具有可行性。

图16 集合能量增强序列功率谱
4 结论
提出了一种基于恒Q变换与二值化能量增强算法以及功率谱分析相结合的故障诊断算法(CQTBEW),该算法对于强噪声环境下获取的信噪比大的滚动轴承振动信号具有较好的分析效果。恒Q变换有对低频有较高频率分辨率以及对高频率较高时间分辨率的特点。本文用恒Q变换对轴承故障信号进行时频分析获得CQT变换矩阵,再利用二值化方法对变换矩阵进行增强处理,最后将矩阵各频率段进行叠加获得原信号的能量增强时间序列,进一步分析提取特征频率。试验表明本算法在强噪声干扰下提取微弱故障特征的问题上是有效的。
