工业互联网项目应用中的风险分担方法研究——以市场需求风险为例

褚晓琳，王家晨

（北京物资学院 经济学院，北京 101149）

一、引言

工业互联网是新一代通信技术与工业系统全方位深度融合形成的产业与应用生态，是第四次工业革命的重要基石。工业互联网在中国的应用发展正处于探索、培育与推广期，需要深入研究如何促进工业互联网与工业体系的深度融合。目前国内学者主要从工业互联网助推制造业转型升级的路径、工业互联网平台企业的发展模式、工业互联网领域的价值共创模式等方面进行了研究。在工业互联网企业和工业企业合作共建项目的实施中，目前制约双方融合发展的一个较为突出的情况是：双方企业只了解各自擅长的专业领域，不熟悉对方的专业领域，因此在项目建设中有时双方会对另一方专业领域的问题产生疑虑，以致较难达成共识。比如，平台企业会担忧市场需求的变化，而工业企业担心项目价值能否合理实现。而这会延缓工业互联网项目的实施，甚至降低项目的落地率。导致双方不熟悉对方专业领域的主要原因在于：工业互联网在中国的发展、应用时间较短，由于该领域专业知识门槛较高，且中国目前已落地的成熟的工业互联网解决方案不多、示范效应不强，因此工业企业对工业互联网的应用价值存在认知不足等问题。而短期内工业互联网企业在工业领域难以形成专业的知识积累，因此较难准确把握工业行业特性与需求难点[1]。要解决上述情况，文章认为可以把出自对方专业领域的问题看成风险，如市场需求风险与项目价值风险等，这些风险由项目双方共同承担，在合作前运用一定的方法进行科学的风险分担，通过合理的风险分担，使双方对各自的风险控制和承受能力有合理的预估，有助于各方做好防范规避，推进项目的顺利实施。文章以工业互联网项目实施中的市场需求风险为例，研究了风险分担方法在该领域的应用。

有关风险分担方法的应用领域，以往的文献较多涉及PPP项目与供应链等领域，国内还没有文献研究风险分担方法在工业互联网领域的应用；有关风险分担方法的研究，国内外学者主要采用统计学和博弈理论的定量研究方法，近年来国内学者运用博弈论的方法较多。一些学者基于讨价还价理论、演化博弈等理论建立博弈模型研究风险分担问题[2，3]。合作博弈Shapley值因其在处理合作中收益及成本的分配时具有天然优势，较多学者也将其应用于合作主体的风险分担分析[4，5]。然而，由于合作博弈Shapley值假设各合作方没有个体差异，但实际上各合作方通常存在一些因素上的明显差异，这些差异会影响各方对风险的控制，为了把这些因素差异考虑在内，有学者通过用因素的权重去修正合作博弈的初始分担，采用修正Shapley值的方法开展研究[6，7]。由于合作博弈Shapley值的计算结果是基于准确的风险损失估计值，然而在风险发生之前，各合作方经常无法准确预估风险损失的实际值，因此合作博弈的计算方案可能有失准确。针对风险损失的不确定性特征，国内外学者已拓宽经典Shapley值的假设条件[8，9]，用区间模糊Shapley值给出了风险分担与收益分配等相关领域的解决方案[10]。

工业互联网项目的市场需求受行业相关政策及标准的调整等外部因素影响，其风险损失值通常难以准确估计，因此文章用区间模糊Shapley值给出了风险损失在各合作方的初始分配。一般各主体的风险控制能力、承担能力以及承担意愿会影响其对风险的控制，而互联网平台企业和制造企业在这些方面有显著差异，丰富的从业经验使制造企业更容易洞察行业需求的变化，因而制造企业较强的风险控制能力以及较好的盈利能力使平台企业的风险承受能力较强，平台企业的风险承担意愿也略高，因此需要综合考虑各主体在这些因素上的差异。由于这些因素之间具有交互影响关系，而ANP法适合计算具有交互影响的因素权重，因此可用ANP法计算各主体关于这些因素的权重，用该权重修正区间模糊Shapley值的初始分配。综上所述，文章运用修正Shapley值的框架，构建了ANP-区间模糊Shapley值的风险分担方法，并将该方法应用于工业互联网项目的市场需求风险分担，以提高各方的合作效率。

二、风险分担方法的构建

1.区间模糊Shapley值方法计算初始风险分担

（1）构造风险损失模糊数

设n人合作博弈用二元组(N，ν(S))表示，N={1，2，…，n}是参与人的集合，n=|N|是参与人的个数，联盟S是N的任意子集，ν(S)是支付函数，ν(S)∶P(N)→R，ν(φ)=0，P(N)是N的全部子集组成的集合。ν(S)可以作为项目的各合作方在不同联盟S的风险损失值，由于在风险发生之前，联盟S的风险损失值ν(S)经常无法准确估计，具有不确定性，这种不确定性可以用模糊数表示，进而将合作博弈扩展到模糊支付合作博弈。设模糊支付合作博弈用二元组(N，ν~(S))表示，ν~(S)∶P(N)→FR+，ν~(φ)=0，FR+是取值为非负的模糊数的集合。ν~(S)可以作为联盟S的不确定的风险损失值。因三角模糊数具有模糊信息易表示、易处理的优势，可以用三角模糊数构造模糊数ν~(S)。为了计算方便，进一步用对称三角模糊数构造。记对称三角模糊数ν~(S)的隶属函数为f(x)，f(x)∶X→[0，1]，x∈X，X为论域。其表达式为：

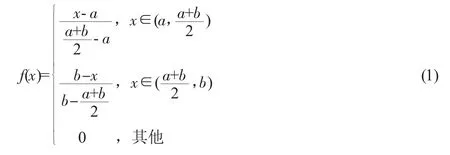
其中，a是三角模糊数ν~(S)的下限，b是三角模糊数ν~(S)的上限，为隶属函数的峰值。三角模糊数ν~(S)的下限可以用ν(S)的下限替代，若可以用作为ν(S)的下限，其中，m为所有可能的联盟数，三角模糊数的上限可以用ν(S)的上限替代，若S⊂Si，则可以用作为ν(S)的上限。

（2）计算风险分担

文章用区间模糊Shapley值求解模糊合作博弈。因为区间模糊Shapley值和经典Shapley都是按照合作方对风险损失减少的贡献分配风险，因此在实际计算中，的含义应是风险损失减少值的模糊数，它的构造可以参照前述风险损失模糊数的构造。对于α∈[0，1]，模糊数的α截集记作分别为该α截集的左右端点。按照区间模糊Shapley值的概念，参照Wan等(2016)的做法[11]，对α∈[0，1]，区间模糊Shapley值可以表示为

2.ANP方法计算合作方关于风险控制影响因素的权重

ANP方法是对层次分析法的扩展。该方法允许同层次的元素之间存在相互影响关系。ANP方法确定合作方关于风险控制影响因素的权重主要有以下几个步骤：

（1）构建风险控制影响因素的网络结构

风险控制影响因素的网络结构由控制层和网络层两部分构成。控制层只有一个目标准则，即风险控制、减少风险损失。网络层由受控制层支配的所有元素集Ci构成，元素集由若干元素组成，这些元素就是风险分担的众多影响因素。元素集之间及元素集内部的各元素之间一般都不独立，可能存在相互影响，网络结果如图1所示。

图1 风险控制影响因素的网络结构

（2）计算元素集内各影响因素的相对权重

设网络层次结构模型网络层的元素集Ci有元素Ci1，Ci2，…，Cin，i=1，2，…，N。以控制层的风险控制为准则，以Cj中元素Cjl为次准则，根据1~9标度法比较元素集Ci中各元素的重要性，以得到各元素的判断矩阵，通过计算得到归一化特征向量该特征向量即为Ci中各元素的C1，C2，…，CN排序向量，可以作为元素集内各影响因素的相对权重，然后进行一致性检验，若C.R.<0.1，则通过检验，否则不通过一致性检验，需要对判断矩阵的元素进行调整，直到满足一致性检验的要求。当l=1，2，…，nj时，可以得到一个矩阵Wij：

Wij的列向量是Ci中元素的权重向量，列向量代表了Ci中的元素关于Cj中的对应元素影响程度的相对重要性，Cj中的对应元素用列向量的上标表示。如果Cj中元素不受Ci中元素的影响，则Wij=0。最终可以得到一个在Ps准则下，由Wij(i=1，2，…，N；j=1，2，…，N)组成的未加权超矩阵W。

（3）计算所有影响因素的权重

在风险控制准则下，运用1~9标度法比较Ci(i=1，2，…，N)个元素集对元素集Cj的相对重要性，通过判断矩阵计算得归一化特征向量(aij，…，aNj)T，当j=1，2，…，N时，得到一个加权矩阵A：

（4）计算合作方关于风险控制影响因素的权重

以元素集内所有的影响因素分别作为准则，运用1~9标度法得到各合作主体的判断矩阵，计算得到各合作主体的排序向量，再结合上一步计算出所有影响因素的风险权重，运用层次分析法可以计算出各主体关于风险控制影响因素的权重。ANP模型的计算借助SD软件进行分析处理。

3.初始风险分担方案的修正

由于区间模糊Shapley值假设各合作方关于影响因素无差异，因此需要修正最初的风险分担方案，以使最终的风险分担方案更合理。修正的过程如下：

设qi是运用ANP法算出的各合作方有关风险分担影响因素的权重，计算Δqi=(qi-1/i)，若Δqi>0时，说明考虑风险控制影响因素后，合作方i控制风险的能力增强，适合增加对其分配的风险；若Δqi<0时，说明考虑影响因素后，对其分配的风险应适当减少。

调整公式是：

修正后的风险分担是：

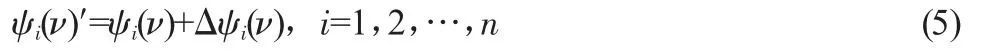
三、案例分析

文章以某工业互联网平台企业与某工程制造企业合作共建智能制造项目为例，分析了风险分担方法在市场需求风险中的应用。该项目原始合同中工业互联网平台企业的投资比重高于制造企业的投资比重。当双方对现有生产计划的市场需求进行研判时，双方意见不一致，平台企业认为现有生产计划的产量过高，平台企业因不了解制造行业的特点，而把握不好现有产品的市场需求，担心一旦市场需求出现变化，现有的生产计划未来可能产生较高的风险损失。若按照投资比重承担风险，较高的风险承担比重会导致其承担的风险损失进一步增加。而制造企业由于其承担风险的比重较低，制造企业可能不会过多地关注风险损失，而是关注较高产量所带来的较高市场占有率和影响力等因素。因此平台企业推进项目的积极性受到影响。因此，可以考虑构建一个公平合理的风险分担方案，促使双方积极合作，达成一致意见，进而推进项目的顺利实施。

1.计算初始分担

如果市场需求变化出现了风险，根据专家评估，若制造企业独立管理该需求风险，可使项目损失值降低820万元。若工业互联网平台企业独立管理该风险，可使项目损失值降低200万元。若制造企业和工业互联网平台企业合作共同管理该风险，可使项目损失值降低1100万元。

设制造企业1、工业互联网平台企业2及双方合作时的风险损失减少值的三角模糊数为：根据式(1)，可写出它们的三角隶属函数，分别是：

根据三角隶属函数，可写出三角模糊数的α截集，见表1。由公式(2)、(3)可得到不同α对应的区间模糊Shapley值区间，见表2。

表2 区间模糊Shapley值的取值区间 （单位：万元）

若工业互联网智能制造项目实际减少的市场需求风险损失值为1074万元，由表1可知，风险损失值减少1074万元位于α截集中心的右侧，范围在1072～1076万元之间，与其对应的显著水平α*位于0.6～0.7之间，由三角隶属函数的性质可计算得出α*=0.65。当α*=0.65时，对求α截集，根据公式(2)、(3)可算出制造企业1的区间模糊Shapley值为[833，847]，工业互联网平台企业2的区间模糊Shapley值为[213，227]。因为所以将区间模糊Shapley值取值的右端点作为制造企业1与平台企业2的风险分担值，分别为847万元与227万元。

表1 三角模糊数α截集 （单位：万元）

2.运用ANP方法计算权重

文章运用ANP方法计算工业互联网智能制造项目各合作方关于影响因素的权重。构建市场需求风险控制影响因素的网络结构，该结构的网络层有3个元素集，分别是：合作方的风险控制能力C1、风险损失承担能力C2与风险承担意愿C3，3个元素集Ci各由3个元素组成，这9个元素就是工业互联网智能制造项目风险控制总的影响因素，如图2所示。

图2 5G+工业互联网智能制造项目风险控制影响因素

风险控制能力C1是指项目各参与方采取相应举措降低风险损失的能力。风险损失的承受能力C2是指项目参与方具有的承担及补偿项目损失的能力。风险承担意愿C3是反映项目参与者具有的承担损失意愿程度的指标。

由图2可以看出，3个元素集之间及元素集内部的各元素之间存在相互关系。首先，分析元素集之间的关系。当参与者具备风险承担意愿，参与者才愿意承担风险，并能够采取措施控制风险。因此风险承担意愿C3是元素集C1与C2的前提条件。反过来，只有参与者对风险有一定的控制能力和承担能力，才会有较强的承担意愿，因此C1与C2这2个元素集也影响C3，故风险控制能力、风险承担能力和风险意愿这3个元素集之间相互影响。其次，分析元素集内部各元素之间的关系，以风险控制能力C1为例，设C1由风险管理者素质、风险管理技术和风险管理经验3个元素组成。风险管理者素质决定了其管理技术和管理经验的高度与深度，而管理技术和管理经验的提高会提升管理者的素质，管理技术与管理经验之间也相互促进。因此风险管理技术、风险管理者素质和风险管理经验3个元素之间相互影响。其他的元素集内元素之间的关系也类似。

文章对工业互联网应用相关领域的专家学者进行了问卷调查。按照1~9标度法对3个元素集Ci之间及各元素集内部元素之间的重要性打分，在专家打分的基础上构建网络层元素集之间和元素之间的判断矩阵，并对判断矩阵进行一致性检验，所有的判断矩阵均通过检验C.R.＜0.1，计算过程中得到未加权超矩阵W和加权超矩阵为：

最后计算极限超矩阵，得到九个影响因素的权重见式(6)：

在工业互联网智能制造项目中存在两个风险分担方：制造企业、工业互联网平台企业。以九个影响因素分别作为准则，结合式(6)，并采用层次分析法计算出两个合作方关于九个影响因素的权重，分别为0.54、0.46。从这两个参与方的综合权重看，两者相差不多，制造企业的权重略高。制造企业在风险控制能力这个指标上取值更大些，而平台企业在风险损失承担能力这个指标上取值更大。整体而言，制造企业的权重略高于平台企业。

3.修正初始风险分担值

由式(4)可以修正初始的风险分担方案，修正结果如下：

由式(7)可以得到制造企业和工业互联网平台企业承担的风险损失减少值分别为889.96万元与184.04万元。对比初始风险分担结果，制造企业承担的风险损失比重增加了，而工业互联网平台企业承担的比重减少了。从最终的计算结果看，制造企业承担的比重高于工业互联网平台企业。对于由市场需求变化带来风险的工业互联网智能制造项目，制造企业更了解项目的市场需求，对市场需求变化的信息更敏感，更容易辨识引起市场需求变动的因素，而平台企业因在制造业领域缺少知识积累，较难全面准确把握市场需求变化，因此制造企业属于风险管控较强的一方，对制造企业分配较多的风险可以促进其积极控制风险，提出合理可行的生产计划，以降低风险发生的可能性并减少成本，避免其因项目投资比重较低而疏于对风险的防范。而平台企业由于在项目中投资比重较高，如果按照投资占比分配风险会增加其控制风险的难度，一旦发生风险，其损失较高，便会阻碍其投资项目的积极性。因此较公平合理的风险分担方案可以有效促进双方规避风险，鼓励双方积极合作共建工业互联网智能制造项目，有助于平台企业为制造业数字化、智能化改造升级提供更全面的解决方案，提升工业互联网对制造业的赋能作用。

四、结论

由于工业互联网项目在中国发展和应用的时间较短，在工业互联网项目的实施中，当各合作方因不熟悉对方专业领域的知识，以致有时较难对另一方相关专业领域的问题达成共识而影响项目推进时，可以借鉴风险管理知识，将出自对方专业领域的问题看成共担风险，用一定的风险分担方法对风险进行科学量化预估，有助于各方防范风险，有效解决相关问题，促进项目的顺利实施。

文章以项目市场需求风险为例，构建了ANP-区间模糊Shapley值的风险分担方法，该方法主要有三个步骤：第一，用区间模糊Shapley值计算风险在各方之间的初始分担。第二，用ANP法对风险分担影响因素赋权，计算各方关于风险分担影响因素的权重。第三，用该权重修正初始风险分担，得到各方最终的风险分担方案。案例分析结果说明了该方法在实践中的可行性，提高了参与方的合作效率。