寒区多孔介质中LNAPL迁移的多场耦合模拟
2022-03-29扶晓琴施小清蒋建国吴吉春
扶晓琴,施小清,蒋建国,吴吉春
寒区多孔介质中LNAPL迁移的多场耦合模拟
扶晓琴,施小清*,蒋建国,吴吉春
(南京大学地球科学与工程学院,表生地球化学教育部重点实验室,江苏 南京 210023)
建立了包含水、气、NAPL、固(冰)四相的温度场、流场及化学场多场耦合模型,适用于定量模拟LNAPL泄漏过程中发生冻结后的迁移分布.通过与非冻条件下LNAPL迁移模型对比,模拟结果显示,冻结条件下因冰的形成LNAPL会发生与非冻条件下不同的迁移行为,冰的形成阻碍LNAPL下渗,并产生冻结势使LNAPL向地表方向迁移.相比非冻结条件,冻结条件下渗达到稳定时LNAPL相的质量通量偏差为-51.1%.冻结条件LNAPL溶解相在水平方向的迁移速度大于非冻结条件,冻结条件下如果不考虑冻结,下渗过程中LNAPL溶解量与挥发量最大偏差分别为2.4%、-24.9%.而冻结条件对LNAPL下渗达到稳定时的溶解量、挥发量影响很小,仅挥发量产生1.8%的偏差.但会减少LNAPL的吸附量,其偏差为-6.6%.
轻非水相流体(LNAPL);多相多场耦合;冻结势;溶质运移
随着石油化工业的发展,非水相有机污染物在其炼制、贮存及运输过程中泄漏至环境,对人类健康造成严重威胁.建立冻结条件下饱和非饱和带的LNAPL迁移模型有利于预测其在寒区泄漏后于土壤-地下水中的迁移分布,为LNAPL污染防控提供技术支撑[1].
NAPL根据密度大小,可分为轻非水相(Light NAPL)和重非水相(Dense NAPL),其控制方程基于多相流理论构建.数值模拟作为一种预测NAPL在土壤—地下水中迁移分布的重要手段,在NAPL污染防治及油气开采中都得到了广泛应用.目前关于三相流在饱和-非饱和带中的模拟已经相对成熟.有关在饱和带中不同降雨速率、介质非均质性及NAPL泄漏速率、地下水流速下的NAPL两相流模型已比较完善[2-10].在非饱和带,相关研究也对NAPL迁移过程进行了数值模拟[11-14].而针对NAPL从非饱和带向饱和带迁移的过程,Lenhard等通过建立自由相、残余相和截留相NAPL与流体水头的函数关系式建立了迁移模型,预测了其分布[15-16].
迄今,寒区冻结条件下LNAPL的迁移研究仍相对较少,研究表明LNAPL在冻结条件下泄漏后在土壤包气带及地下水中的迁移因为冰晶影响会与非冻结条件下的迁移图像有所不同,冰晶有效阻止石油垂直迁移,加强石油沿优先流路径下渗及在地表浅层水平流动,但即使完全冰饱和的土也表现出一定的冰渗透性[17-19].且在冻结条件下,土壤包气带伴随冻结滞水的形成,饱和水汽压作用减小,而毛管作用得以加强[21],地下水中神经节状Ganglia在冻结势和基质势作用下会向冻结峰积聚,且有部分LNAPL汇聚于表层[20,22].国内也有少数学者通过室内冻结箱实验开展LNAPL于冻结条件下的迁移规律研究[22-23].然而由于冻结固相(冰)的存在,需将温度场与LNAPL迁移所涉及的渗流场、化学场耦合,同时多相多场耦合问题求解往往不易收敛,有关冻结条件下气相、水相、NAPL相三相运移模拟尚未见相关报道.
COMSOL Multiphysics软件常用于多场多相问题的求解.而冻结条件下LNAPL的迁移,涉及到水、气、NAPL三相在多孔介质中运移,是温度场、流场及化学场多场耦合的问题.已有的COMSOL模块设置中缺少冻结模块,无法直接用于建立冻结条件下LNAPL迁移模型.本研究通过在COMSOL中增设冻结过程控制方程对冻结条件下LNAPL入渗过程进行模拟,建立固相-气相-水相-NAPL相四相共存,温度场、流场、化学场三场耦合模型,模拟冻结条件下LNAPL在饱和-非饱和带的迁移行为及分布形态,旨在克服LNAPL迁移模拟模型中未考虑冰相而无法适用于寒区的缺陷.
1 冻结条件下多孔介质中LNAPL迁移的数学模型
1.1 数学模型的建立
冻结条件下多孔介质LNAPL迁移因有冻结固相(冰)存在,需要在以往三相流运移方程的水相运移质量守恒方程中加入冰相,并通过未冻水和冻结冰的经验关系式实现温度场和流场的耦合.
冻结条件下LNAPL的迁移包括两个过程,一是LNAPL自由相在水-气-LNAPL-冰四相共存时的毛细压力作用下迁移,二是溶于水的LNAPL及其挥发在空气中的LNAPL的溶质迁移过程,以对流-弥散作用为主.该过程涉及水-冰相变、水-气-NAPL三相流迁移、多孔介质温度传导及溶质运移模型耦合,其控制方程如下:
1.1.1 水-气-NAPL-固(冰)四相控制方程 据各相的质量守恒定律[16,24]得到:

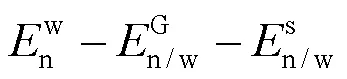

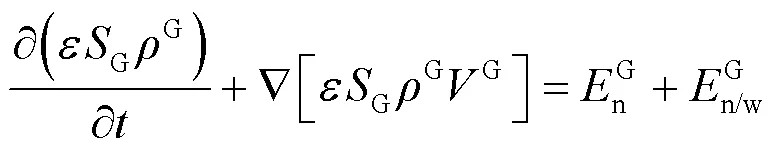

自由相LNAPL在水中的溶解过程用式(4)表达[26]:
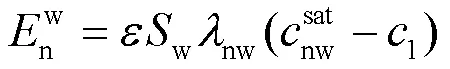
自由相LNAPL挥发于空气可用式(5)表达[26]:
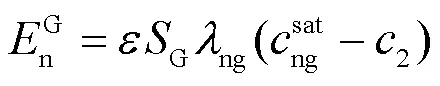
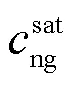
溶于水的LNAPL挥发于空气可用式(6)表达[26]:
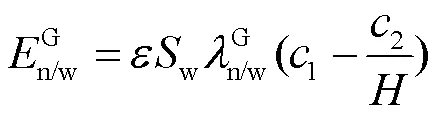
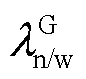
溶于水中的LNAPL吸附于土壤骨架可用式(7)表示[27]:
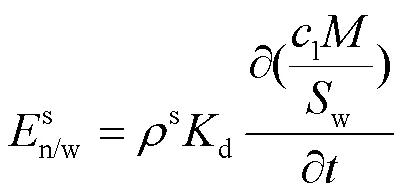
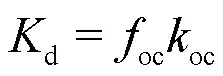
式中:oc为土体中有机碳的质量分数;oc为有机碳分配系数.
而对于毛管压力CNW、CGN以及相对渗透率rW、rN、rG,需构建--关系式.本模型-关系将van Genuchten方程拓展到三相流[28],得到:

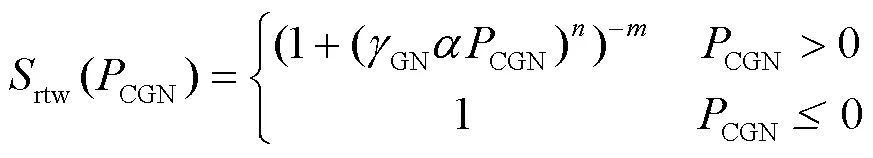
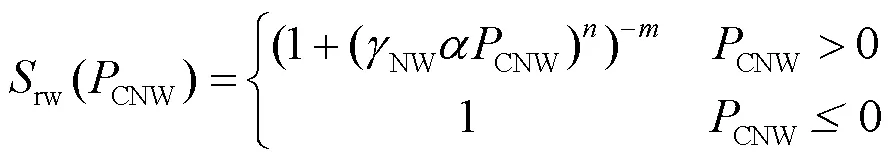
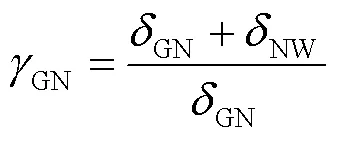
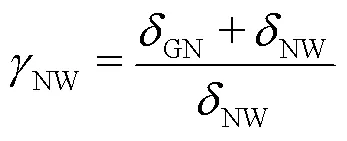
而对于饱和渗透率,它随冻结过程孔隙度的变化而变化(将冰视为土壤固体骨架来实现水-气-NAPL-固四相向水-气-NAPL三相的转换),采用Kozeny-Carman模型[29],表达式如下:

式中:为颗粒直径.
1.1.2 多孔介质传热 多孔介质传热方程即热量守恒方程如下:

式中:为流体密度;p为比定压热容;为达西流速;为温度;eff为热导率;f为融化潜热[24].
为了实现温度场与三相流场的耦合,一方面需要引入冻结条件下未冻水和冻结冰的经验比例关系式[30](式16),另一方面,通过将冰视为土壤固体骨架来实现水-气-NAPL-固四相向水-气-NAPL三相的转换,即冻结过程中固体骨架的孔隙度将随冰的形成而不断变化,且传热方程中的比热容和导热系数是水-气-NAPL-固四相体积占比的加权函数.
冻结场和三相流场的耦合关键即未冻水与冻结冰的经验比例式如下:
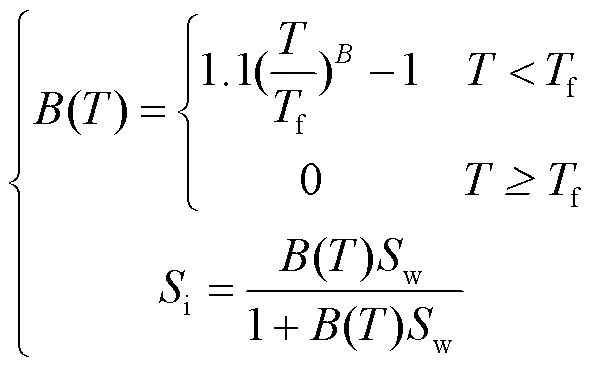
式中:()为比例系数;f为起始冻结温度(绝对温度);系数1.1为水与冰的密度之比.
1.1.3 溶解相-挥发相LNAPL质量平衡方程 LNAPL溶解相的溶质运移方程为:

LNAPL挥发相的溶质运移方程为:

式中:为LNAPL的物质的量质量分数;W、G为水动力弥散系数.
非冻结条件下LNAPL迁移的控制方程除水相运移方程(式1)不包含含冰项及无需进行多孔介质温度传导模块设置外,其余控制方程与冻结条件下LNAPL迁移控制方程一致.
1.2 模型求解
采用COMSOL Multiphysics的多孔介质多相流模块、多孔介质温度传导模块、多孔介质物质传递模块及达西定律模块输入并求解冻结条件下LNAPL迁移控制方程.COMSOL Multiphysics是一款强大的多物理场耦合软件,常用于多场多相问题的求解.而冻结条件下LNAPL的迁移,涉及到水、气、NAPL三相在多孔介质中运移,是温度场、流场及化学场高度耦合的问题.COMSOL中水相方程并未包含冰相,故在模拟冻结时需要在水相质量守恒方程中加入冰相随时间变化(式1).而气相、LNAPL相则采用其内置方程(式2~3).COMSOL内置的多孔介质相传递模块可用来模拟三相流运移,但其未考虑四相质量转换过程,需要在模块中增设(式4~8).毛管压力以及相对渗透率也需要在COMSOL中自行构建其与相对饱和度间的关系式(式9~13).多孔介质温度传导模块可用来模拟介质传热,但其热传导方程缺少冰的融化潜热项,需要在源项增设(式15).而且其缺少冻结方程设置模块,需将冻结条件下未冻结水和冻结冰的经验比例关系式(式16)在COMSOL中进行设置.
对于非冻条件下LNAPL迁移模型,可采用COMSOL的多孔介质多相流模块、多孔介质稀物质传递模块及达西定律模块输入并求解LNAPL迁移控制方程.同样将四相质量转换过程在多孔介质相传递模块中进行增设.而三相流运移控制方程均采用COMSOL内置方程.
COMSOL通过有限单元法离散上述模型,以求解冻结、非冻结条件下LNAPL迁移的非稳定问题.冻结、非冻结条件下LNAPL迁移模拟输出结果中自由相LNAPL的含量用饱和度表示,溶解相及挥发相LNAPL含量用质量浓度表示.
2 算例验证
2.1 算例概述及初始边界条件
算例改自文献[26]所建立的数值模拟算例,文献[26]中的算例研究了LNAPL定点泄漏后于土壤多孔介质中的迁移行为.本文采用与该算例相同的水文地质条件和污染物泄漏条件建立冻结条件下LNAPL迁移模型.为验证本次所构建冻结条件LNAPL迁移模型的可靠性,首先利用所建立的模型开展非冻结条件下模拟,并与文献[26]中结果进行对比验证.进而在非冻条件下LNAPL迁移模型中加入冰相、温度场和流场的耦合方程及冻结相关边界条件进行了冻结条件下LNAPL在多孔介质中的二维迁移模拟.
建立的冻结条件下LNAPL在非饱和带中二维迁移数值算例见图1.研究区为二维剖面,长1.5m,厚1.5m,下部0.5m为地下水饱和区,取地下水面为基准面.区域网格剖分采用COMSOL的物理场细化网格剖分.
至于初始条件,对于非饱和带与饱和带分别进行如下设置:

模型的边界条件如下设置:
(1)流场
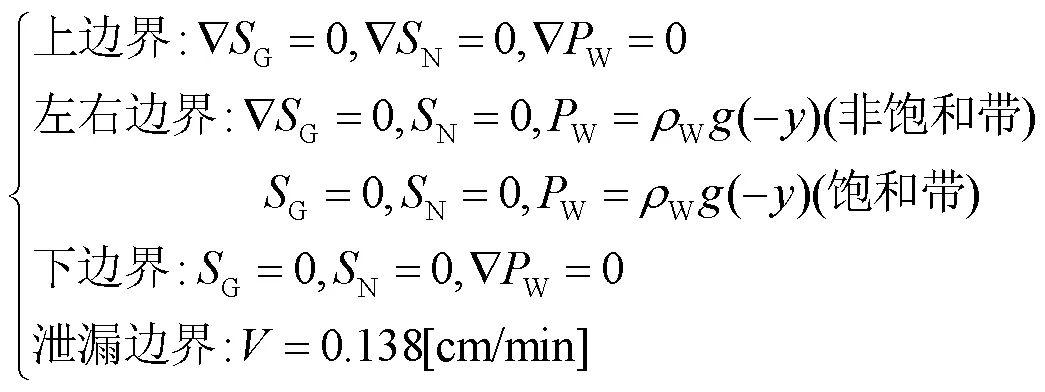
(2)化学场
(3)温度场
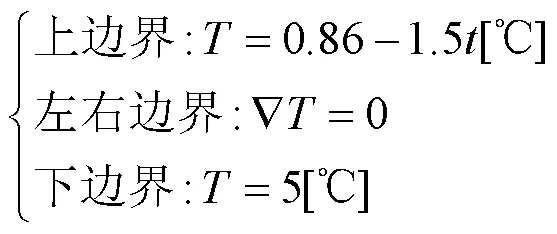
初始边界条件如图1.对于非冻结条件下,无需设置温度场边界及初始条件,流场和溶质场边界条件及初始条件与冻结条件下保持一致.
2.2 基本参数
模型中采用的参数值如表1,包括土壤、水、LNAPL、冰的特征参数以及三相质量转换的相关参数.LNAPL在此以甲苯为模拟对象.

表1 模型相关参数
2.3 情景设置
设置冻结条件与非冻结条件LNAPL下渗2种情景进行模拟,通过模拟结果对比来探究冻结条件对LNAPL迁移影响.非冻结条件下除温度场外,其它条件与冻结条件下保持一致.
3 结果与讨论
3.1 温度场
冻结过程中温度随冻结时间增长在地表浅层由0℃逐渐降低至-14℃(图2),冰饱和度在地表浅层逐渐增加,冻结12h时,地表浅层冰饱和度达到0.8(图3).因为温度只在上部薄层发生变化,下部恒为5℃,故取土壤表层0.1m厚的温度场模拟结果进行分析.可知冻结场在很短时间内达到稳定,温度在土壤表层骤降,在土壤表层会形成薄冰层.这再现了低温条件下多孔介质LNAPL、水迁移实验所得实验结果:低温环境中LNAPL相迁移时高温区域面积较大,等温线在土壤表层较为密集,温度梯度变化较快[23].说明LNAPL泄漏会对土壤的对流传热产生影响,对土壤起保温作用.LNAPL流经薄冰层时,顺着薄冰层做水平方向流动.而当流体做水平方向流动时,在垂直于流动方向的热量传递,主要以热传导方式进行.LNAPL流体的导热系数较小,传热热阻主要集中在该层中,温差也集中在该层[31].且达西数较小时,也会明显削弱对流传热[32].
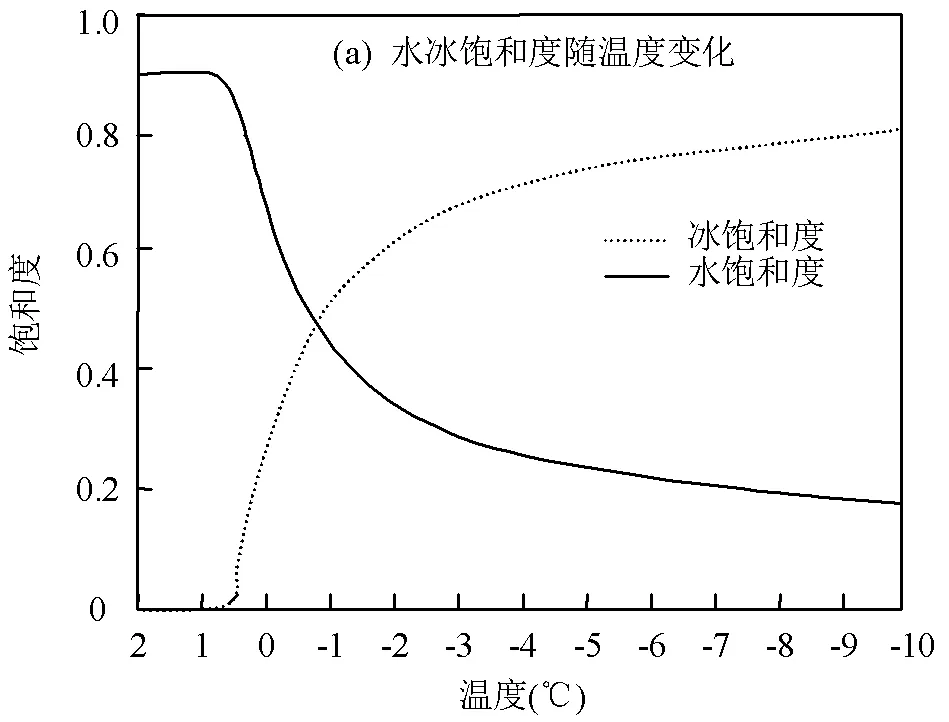
在近地表冻层处取坐标为(0.75m,0.98m)的点A(图1)为代表性点进行进一步分析,该点处空隙里的水组分和冰含量随温度变化的情况如图4(a)所示.随温度降低至冻结温度0.3℃时,冰饱和度由0逐渐增加,而水饱和度随温度降低逐渐减小.温度达到-10℃时,水饱和度仅为0.17,而冰饱和度达到0.80.而该点处的水相、冰相随时间的变化及由水冰相变造成的潜热变化如图4(b)所示.水饱和度在未冻结前期随LNAPL下渗水压增大而增加,后趋于稳定(图4(c)).而随温度下降至0摄氏度时(图4(a)),即在第2h时冰饱和度由0逐渐增加,同时水饱和度减小,水相转化为冰相.而潜热伴随这一过程释放,达到峰值后下降,随冻结速度变慢而降低,当到达12h时,冻结达到稳定,潜热趋于零(图4(b)).
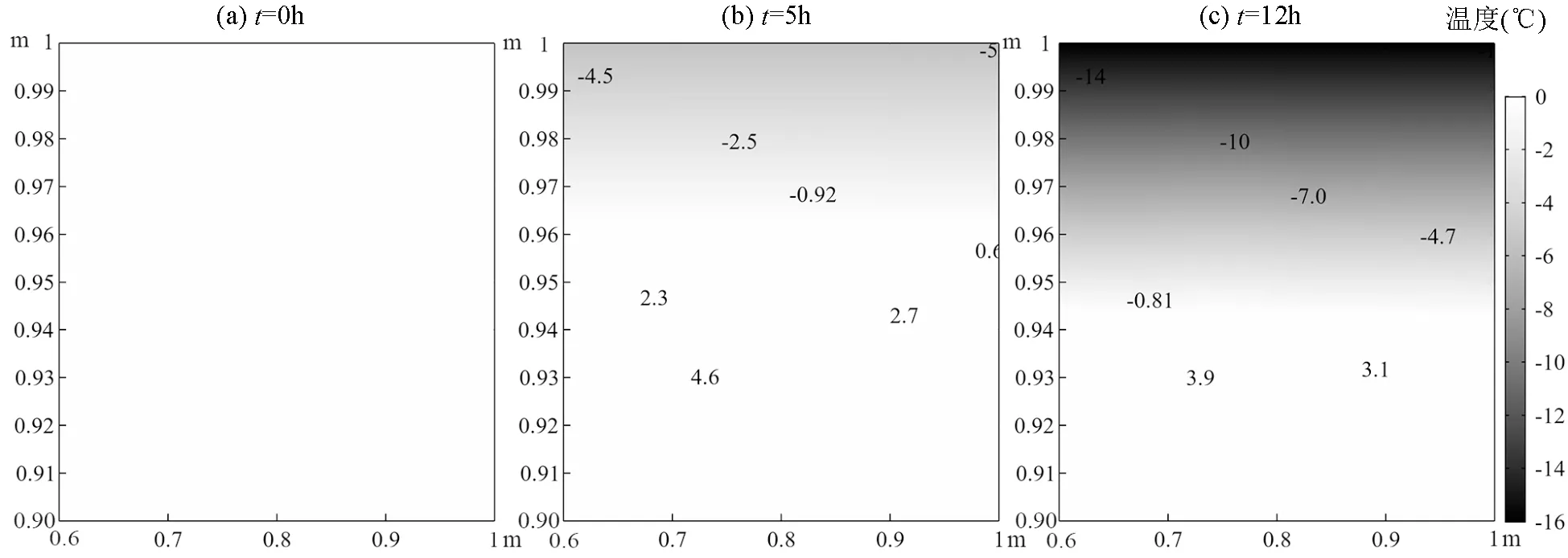
图2 温度场随时间的演变过程

图3 含冰率随时间的演变过程
3.2 流场
3.2.1 冻结条件下LNAPL迁移特征 如图5(a)所示,冻结前5h LNAPL在重力作用下向下迁移,在含冰层下端有突变界面,LNAPL含量在泄漏点的冻层处聚集.对冻结层点A处(图1)的孔隙率和渗透率进行分析,可知当温度随时间增长降至冻结温度时,由于水相转换为冰,介质孔隙度变小,而渗透率随孔隙度的减小而降低(图6),即冻层对LNAPL的下渗有明显阻挡作用.而随着冻结作用增强,LNAPL不再继续向下迁移.冻结5h后,其在冻结势的作用下克服重力势作用向上迁移[21],迁移程度较小,随后达到稳定.而对于包气带中的水分,其在冻结前1h内向上运移(图5(b)),由图5(c)压力分布及流线图,地表土层处水压逐渐升高,流线向上,可知趋使水分向上运移的是随LNAPL下渗产生的压力变化.随后其饱和度随LNAPL污染晕的移动而变化,含冰层处水分转化为冰,水饱和度相对较低(图5(b)).包气带中的气体则随LNAPL的下渗逐渐向边缘扩散,直至整个区域被LNAPL和水分填充.且其在含冰层下部出现模拟高值,发生聚集(图5(d)).

如图7所示,由冻结5h和冻结12h的量分布剖面图可知,LNAPL向下泄漏,其量由泄漏表面至深部逐渐减少.而且LNAPL从冻结5h至冻结12h量分布曲线上移,剖面上LNAPL量均有不同程度减小,在冻结势作用下向地表方向迁移,暴露在表层.以冻结层浓度减小最明显,最高可达5mg/L.而在冻结层下部量减少较小,这是因为下部LNAPL向上迁移,会受到冻层阻滞,形成累积,这与李兴柏等[22]对冻结条件下的石油迁移试验结果一致.故下部迁移的LNAPL累积量抵消了部分LNAPL的向上迁移量.由模拟结果计算得冻结条件下前5h LNAPL向下迁移量为21.24mL,而冻结5h~冻结12h LNAPL向上迁移至土壤表层的量为1.04mL.
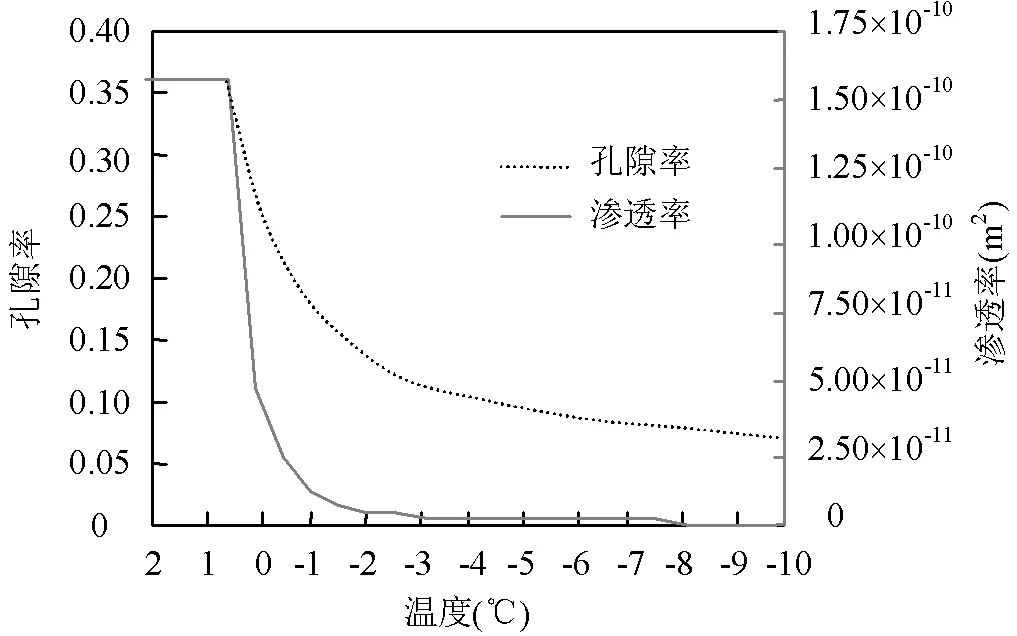
图6 渗透率及孔隙度随时间变化
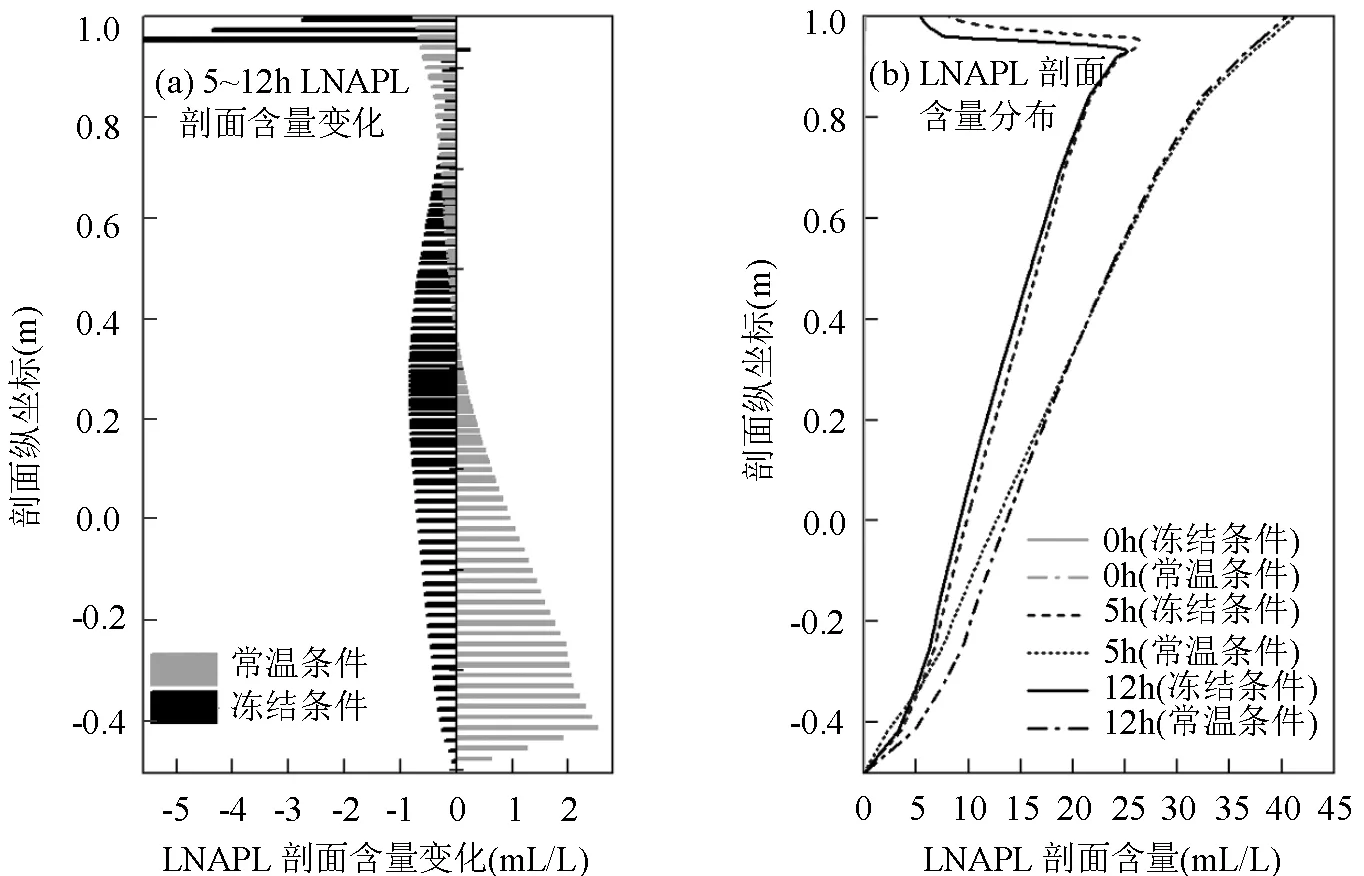
图7 LNAPL运移量的垂向分布
3.2.2 非冻结条件下LNAPL迁移特征 如图8所示,LNAPL随时间推移逐渐向下渗透,前5h变化程度大,随后达到区域饱和稳定状态.非冻结条件下LNAPL运移5和12h相比的量分布差异以及向下泄漏量分布剖面变化如图7所示,可知LNAPL在非冻结条件下在重力势作用下向下渗,其量同样由泄漏表面至深部逐渐减少.在第5h~第12h,上部土壤水带和中间带LNAPL浓度略有减少,LNAPL向下迁移,在下部地下水饱和带以及毛细水带累积,而且泄露源对上部土壤水带和中间带的补给量小于其向地下水饱和带及毛细水带的下渗量.由模拟结果计算得非冻结条件下前5h LNAPL向下迁移量为38.59mL,至第12h达到41.30mL.
非冻结条件与冻结条件下LNAPL下渗模拟结果相比,因其不存在冻结层的阻挡作用,下渗速度快,下渗量远大于冻结时下渗量.12h后地下水面处体积分数可达0.040(图8),而冻结条件下地下水面土壤处LNAPL体积分数仅达0.016(图5(a)).非冻结条件LNAPL向地下水面迁移,不存在向上迁移现象,而冻结条件下LNAPL在冻结5h后在冻结势作用下发生向上迁移(图7).冻结条件下LNAPL相的下渗量相比非冻结条件下的量产生-51.1%偏差.
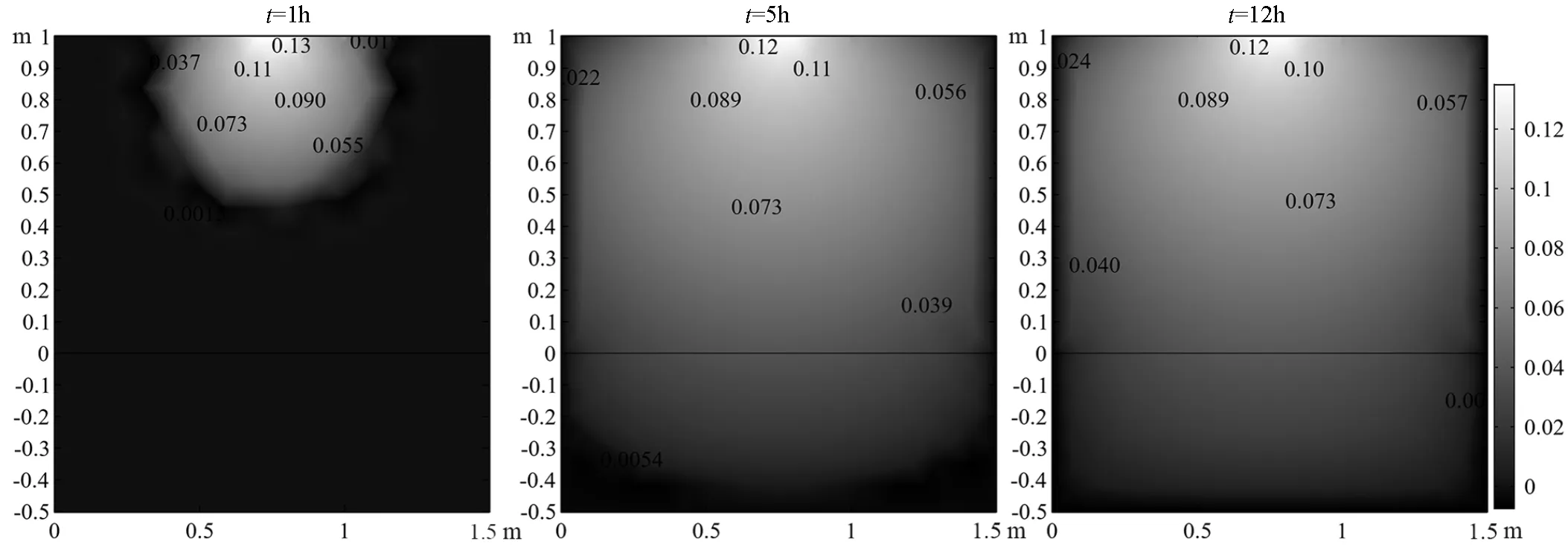
图8 常温条件下LNAPL饱和度变化
3.3 化学场
3.3.1 冻结条件LNAPL溶解挥发相迁移特征 如图9(a)所示,随LNAPL下渗,其在水中的溶解度逐渐增加,随后趋于稳定状态.冻结1h时,LNAPL溶解相分布图像呈椭圆型,在地下水中浓度达116.5mg/L.迁移1h时,LNAPL挥发相在包气带中浓度可达118.7mg/L.冻结稳定后,在LNAPL以0.138cm/min的泄漏速度下,其在包气带中浓度可达186.7mg/L (LNAPL在水中的溶解度为515mg/L).而冻结条件下LNAPL挥发相随气相逐渐向两边扩散(图9(b)),在土壤表层浓度可达101.0mg/L(LNAPL在空气中的溶解度为139mg/L).
模拟可得冻结条件下不同状态LNAPL含量关系图,如图10所示.可知冻结条件下冻结1h时总溶解量为0.304mL,挥发量为0.195mL.冻结稳定时LNAPL总下渗量为23.74mL,溶于水的量为0.48mL,气相LNAPL含量为0.165mL,而LNAPL吸附量为2.71mL(图10(a)).冻结条件下12h时可自由移动LNAPL量(溶解相LNAPL与自由相LNAPL的和)为20.68mL,其含量在冻结前5h逐渐增加,从冻结5h后的21.72mL逐渐减少,减少量为冻结势作用下向土壤表层迁移量.而吸附量随冻结时间增长增加到2.71mL后保持稳定(图10(b)).
3.3.2 非冻结条件LNAPL溶解挥发相迁移特征 如图11(a)所示,水中的溶解相随LNAPL下渗逐渐增加,随后稳定.迁移1h时,LNAPL溶解相分布图像呈楔形,其在垂直方向扩散速度大于水平方向,在地下水饱和区浓度可达117.2mg/L.迁移1h时,LNAPL挥发相在包气带中浓度可达143.2mg/L.下渗稳定后,在LNAPL以0.138cm/min的泄漏速度下,LNAPL溶解相在包气带中浓度可达185.8mg/L(LNAPL在水中的溶解度为515mg/L).而非冻结条件下LNAPL挥发相随气相逐渐向两边扩散(图11(b)),在土壤表层浓度可达101.9mg/L(LNAPL在空气中的溶解度为139mg/L).

图9 冻结条件下LNAPL溶解相和挥发相浓度分布
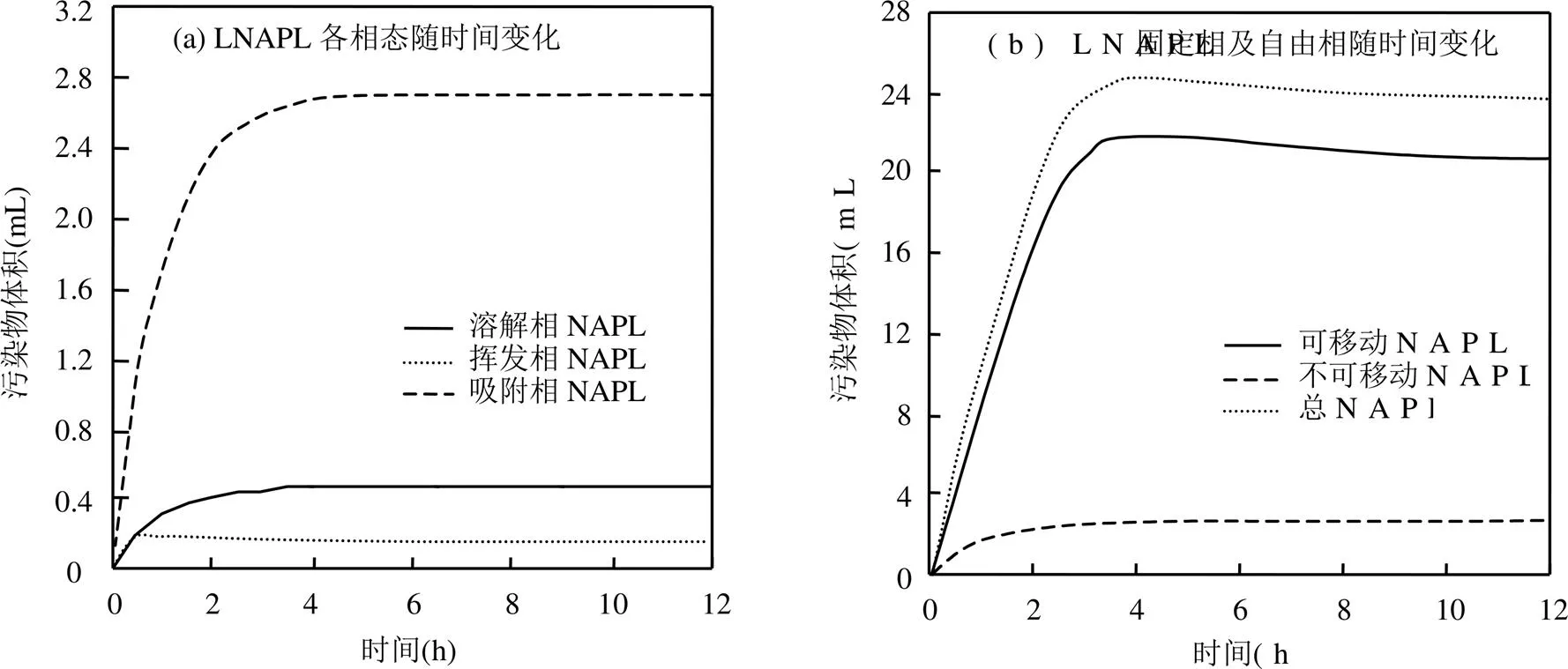
图10 冻结条件不同状态LNAPL含量变化
非冻结下不同状态LNAPL含量关系图如图12所示.溶解相LNAPL、挥发相LNAPL及吸附相LNAPL随冻结时间增长逐渐增多,达到稳定时含量吸附相LNAPL远大于溶解相,而挥发相最少(图12(a)).可知非冻结条件下下渗1h时总溶解量为0.196mL,挥发量为0.251mL.稳定后LNAPL总下渗量为41.30mL,溶于水的量为0.48mL,气相LNAPL含量为0.168mL,LNAPL吸附量为2.90mL(图12(a)).吸附量占泄漏总量7%,吸附量大于溶解量,这也与Kim和Corapcioglu 的LNAPL泄漏实验结果吻合[33].非冻结条件LNAPL从泄漏点开始不断下渗,至第7h达到38.43mL稳定状态,吸附量随冻结时间增长增加到2.90mL后保持稳定(图12(b)).而可移动的LNAPL相(包括溶解相和自由相)略有减少后趋于稳定.

图11 常温条件下LNAPL溶解相和挥发相浓度分布

图12 常温条件不同状态LNAPL含量变化
对比LNAPL于冻结、非冻结条件下1h时溶解相、挥发相浓度分布可知,LNAPL溶解相在冻结条件下在水平方向上扩散速度大于非冻结条件,地下水饱和区溶解相浓度差为0.7mg/L,土壤非饱和带中LNAPL挥发相最大浓度之差为24.6mg/L.在下渗过程中LNAPL溶解量与挥发量冻结条件相比非冻结条件会产生2.4%、-24.9%的最大偏差.稳定时LNAPL在水中及空气中的溶解扩散量浓度差别在1mg/L内,其受冰冻层影响小.又由不同状态LNAPL含量变化图可知两种情景下LNAPL溶于水的量相等,而气相LNAPL含量差仅为0.003mL,偏差为-1.8%.即含冰层对LNAPL的溶解量和挥发量造成的影响很小,这是因为冻结条件下溶解量和挥发量主要通过分子扩散作用通过冰晶孔隙,含冰层的存在对分子扩散作用影响小.而对比吸附量,非冻结条件LNAPL吸附量高于冻结条件LNAPL吸附量,偏差为-6.6%.这是因为一方面LNAPL在非冻结条件下下渗量大于冻结条件,另一方面土壤表面被冰包裹会减少土壤的比表面积从而降低其吸附性能.
3.4 模型验证
所建模型未加入冻结模块时,与文献[26]建立的水文地质条件及污染物泄漏条件设置一致.故可用文献[26]的模拟结果与本模型模拟结果进行对比以验证所建模型可靠性.由图13可以看出,两者模拟结果一致,验证了所建模型在非冻结条件下的正确性.
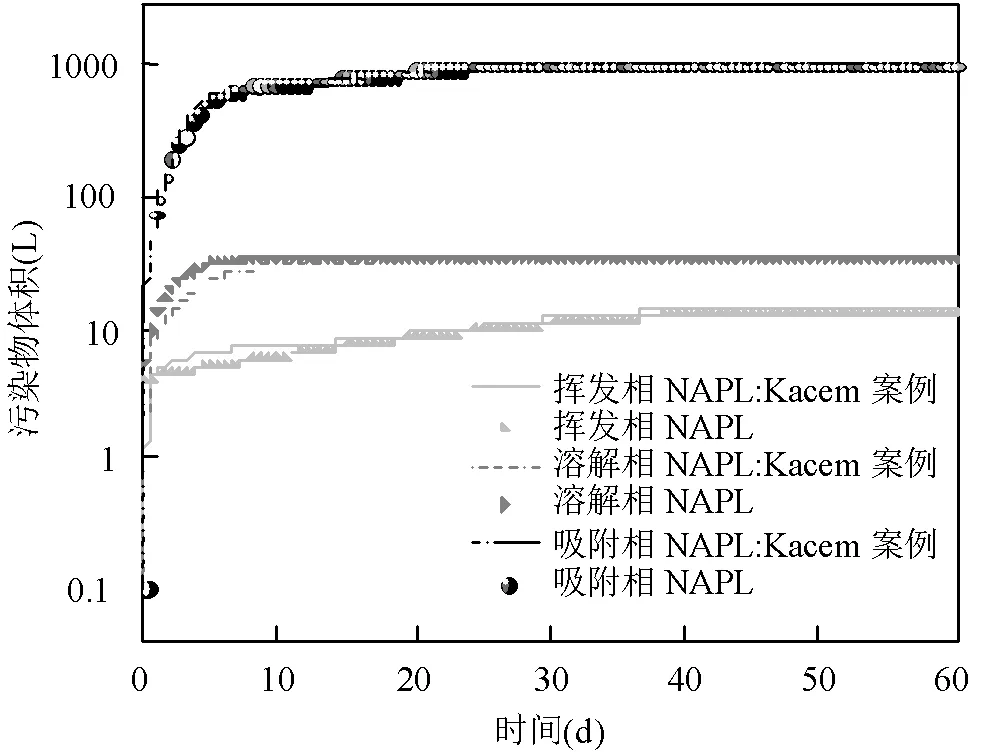
图13 模型与Kacem案例不同相态LNAPL含量变化对比
所建模型在冻结条件下的可靠性,由于相关研究较少,难以找到相关实验数据直接验证.后续可开展冻结条件下多相流迁移实验来进一步验证模型.
4 结论
4.1 本文在COMSOL Multiphysics的多孔介质相传递、多孔介质温度传导、多孔介质物质传递模块的基础上,通过增设相关模块构建了包含水、气、LNAPL、冰四相的温度场、流场及化学场三场耦合模型.可用于模拟及定量刻化LNAPL泄漏过程中发生冻结后LNAPL的迁移分布,为寒区LNAPL泄漏后的修复提供参考.
4.2 LNAPL在地表浅层的泄漏会影响土壤与环境的热量传导过程.在靠近薄冰层处总有一薄层流体顺着薄冰层做水平流动,而冰层介质的达西数较小,会明显削弱土壤的对流传热,形成热阻层,使得温度骤变界面在薄冰层产生.
4.3 冻结条件下LNAPL迁移及水分运移受重力势、基质势及冻结势的控制,LNAPL先在重力势下向下迁移,随冻结时间增长,冻结势和重力势平衡后在冻结势作用下发生一定程度的向上迁移.冻结条件下LNAPL相的下渗量相比非冻结条件下的量产生-51.1%的偏差.
4.4 冻结条件LNAPL溶解相在水平方向迁移速度大于非冻结条件,下渗过程中冻结条件LNAPL溶解量与挥发量相比非冻结条件会产生2.4%、-24.9%的最大偏差,下渗达到稳定时仅挥发量产生1.8%的偏差.溶解量和挥发量主要通过分子扩散作用通过冰晶孔隙,含冰层的存在对分子扩散作用影响小.而含冰层的存在对吸附量存在影响,冻结条件下LNAPL吸附量略低于非冻结条件下LNAPL吸附量,偏差为-6.6%.
[1] 李国玉,马 巍,李兴柏,等.多年冻土区石油污染物迁移过程研究回顾与展望 [J]. 冰川冻土, 2011,33(4):947-952.
Li G Y, Ma W, Li X B, et al. Migration of the petroleum pollutants in permafrost regions: Review and prospect [J]. Journal of Glaciology and Geocryology, 2011,33(4):947-952.
[2] 施小清,吴吉春,刘德朋,等.饱和介质中重非水相液体运移的数值模拟及敏感性分析 [J]. 南京大学学报(自然科学版), 2011,47(3):299- 307.
Shi X Q, Wu J C, Liu D P, et al. Numerical simulation of transportation of dense nonaqueous phase liquids in the subsurface environment [J]. Journal of Nanjing University (Natural Sciences), 2011,47(3):299-307.
[3] Yang Z B, Zandin H, Niemi A, et al. The role of geological heterogeneity and variability in water infiltration on non-aqueous phase liquid migration [J]. Environmental Earth Sciences, 2013,68(7): 2085-2097.
[4] 王 涵,卢文喜,李久辉,等.地下水DNAPLs污染多相流的随机模拟及其不确定性分析 [J]. 中国环境科学, 2018,38(7):2572-2579.
Wang H, Lu W X, Li J H, et al. Stochastic simulation and uncertainty analysis of multi-phase flow of groundwater polluted by DNAPLs [J]. China Environmental Science, 2018,38(7):2572-2579.
[5] 郑 菲,高燕维,施小清,等.地下水流速及介质非均质性对重非水相流体运移的影响 [J]. 水利学报, 2015,46(8):925-933.
Zheng F, Gao Y W, Shi X Q, et al. Influence of groundwater flow velocity and geological heterogeneity on DNAPL migration in saturated porous media [J]. Journal of Hydraulic Engineering, 2015,46 (8):925-933.
[6] Van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils [J]. Soil Science Society of America Journal, 1980,44(5):892-898.
[7] Brooks R H, Corey A T. Properties of porous media affecting fluid flow [J]. Journal of the Irrigation and Drainage Division, 1966,92(2): 61–90.
[8] Falta R W, Pruess K, Javandel I, et al. Numerical modeling of steam injection for the removal of nonaqueous phase liquids from the subsurface: 1. Numerical formulation [J]. Water Resource Research, 1992,28(2):433–449.
[9] Adenekan A E, Patzek T W, Pruess K. Modeling of multi-phase transport of multicomponent organic contaminants and heat in the subsurface: Numerical model formulation [J]. Water Resource Research, 1993,29(11):3727–3740.
[10] White M D, Oostrom M, Lenhard R J. Modeling fluid flow and transport in variably saturated porous media with the STOMP simulator. 1. Nonvolatile three-phase model description [J]. Advances in Water Resources, 1995,18(6):353–364.
[11] 阮冬梅,卞建民,王 倩,等.低渗透介质中轻非水相流体迁移转化规律 [J]. 中国环境科学, 2021,41(4):1815-1823.
Ruan D M, Bian J M, Wang Q, et al. The migration and transformation of light non-aqueous fluid in silty clay [J]. China Environmental Science, 2021,41(4):1815-1823.
[12] Hofstee C, Lenhard R J, et al. Flow behavior and residual saturation formation of liquid carbon tetrachloride in unsaturated heterogeneous porous media [J]. Journal of Contaminant Hydrology, 2003,64(1):93-112.
[13] Lo I M, Hu L M, Meegoda J N. Centrifuge modeling of light nonaqueous phase liquids transport in unsaturated soils [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004,130(5):535-539.
[14] Kechavarzi C, Soga K, Lllangasekare T H. Two-dimensional laboratory simulation of LNAPL infiltration and redistribution in the vadose zone [J]. Journal of Contaminant Hydrology, 2005,76(3/4): 211–233.
[15] Lenhard R J, Rayner J L, Davis G B. A practical tool for estimating subsurface LNAPL distributions and transmissivity using current and historical fluid levels in ground water wells: Effects of entrapped and residual LNAPL [J]. Journal of Contaminant Hydrology, 2017,205: 1–11.
[16] Kacem M, Esrael D, Boeije C S, et al. Multiphase Flow Model for NAPL Infiltration in Both the Unsaturated and Saturated Zones [J]. Journal of Environmental Engineering, 2019,145(11):04019072.
[17] Biggar K W. Site investigations of fuel spill migration into permafrost [J]. Journal of Cold Regions Engineering, 1998,12(2):84–104.
[18] Chuvilin E M, Naletova N S, Miklyaeva E C, et al. Factors affecting spreadability and transportation of oil in regions of frozen ground [J]. Polar Record, 2001,37(202):229-238.
[19] Barnes D L, Wolfe S M. Influence of Ice on the Infiltration of Petroleum into Frozen Coarse-grained Soil [J]. Petroleum Science and Technology, 2008,26(7/8):856-867.
[20] Singh K, Niven R K. Non-aqueous Phase Liquid Spills in Freezing and Thawing Soils: Critical Analysis of Pore-Scale Processes [J]. Critical Reviews in Environmental Science and Technology, 2013, 43(6):551-597.
[21] 徐树林,那平山,武俊英.关于冻结滞水的探讨 [J]. 内蒙古林学院报, 1994,(2):46-51.
Xu S L, Na P S, Wu J Y. An approach to frozen perched groundwater [J]. Journal of inner Mongolia forestry college, 1994,(2):46-51.
[22] 李兴柏,李国玉.温度梯度对多年冻土区石油迁移影响的研究 [J]. 甘肃科学学报, 2013,25(1):73-76.
Li X B, Li G Y. Experimental study on the influence of temperature gradient on the migrating process of oil contaminants in permafrost regions [J]. Journal of Gansu Sciences, 2013,25(1):73-76.
[23] 吴国忠,赵文浩,吕 妍,等.多孔介质内油、水介质迁移对比低温实验[J]. 当代化工, 2016,45(6):1108-1111.
Wu G Z, Zhao W H, Lv Y, et al. Comparison of the migration of oil and water in porous medium with cryogenic experiment [J]. Contemporary Chemical Industry, 2016,45(6):1108-1111.
[24] Zhang M L, Wen Z, Xue K, et al. A coupled model for liquid water, water vapor and heat transport of saturated–unsaturated soil in cold regions: model formulation and verification [J]. Environmental Earth Sciences, 2016,75(8):1-19.
[25] 胡黎明,邢巍巍,吴照群.多孔介质中非水相流体运移的数值模拟 [J]. 岩土力学, 2007,28(5):951-955.
Hu N M, Xin W W, Wu Z Q. Numerical simulation of non-aqueous phase liquids migration in porous media [J]. Rock and Soil Mechanics, 2007,28(5):951-955.
[26] Kacem M, Benadda B. Mathematical model for multiphase extraction simulation [J]. Journal of Environmental Engineering, 2018,144(6): 04018040.
[27] 高彦斌,张松波,李 韬,等.饱和黏性土中重质非水相有机污染物纵向迁移数值模拟[J]. 同济大学学报(自然科学版), 2020,48(1):24- 32.
Gao Y B, Zhang S B, Li T, et al. Numerical analysis of vertical migration of dense nonaqueous-phase liquids in saturated clay [J]. Journal of Tongji University (Natural Science), 2020,48(1):24-32.
[28] Parker J C, Lenhard R J, Kuppusamy T. A parametric model for constitutive properties governing multiphase flow in porous media [J]. Water Resource Research, 1987,23(4):618-624.
[29] Peng X, Yu B. Developing a new form of permeability and Kozeny–Carman constant for homogeneous porous media by means of fractal geometry [J]. Advances in Water Resources, 2008,31(1):74-81.
[30] 白青波,李 旭,田亚护,等.冻土水热耦合方程及数值模拟研究 [J]. 岩土工程学报, 2015,37(S2):131-136.
Bai Q B, Li X, Tian Y H, et al. Equations and numerical simulation for coupled water and heat transfer in frozen soil [J]. Chinese Journal of Geotechnical Engineering, 2015,37(S2):131-136.
[31] 刘 伟,范爱武,黄晓明.多孔介质传热传质理论与应用 [M]. 北京:科学出版社, 2006:28-30.
Liu W, Fang A W, Huang X M. Theory and Application of Heat and Mass Transfer in Porous Media [M]. Beijing: Science Press, 2006:28- 30.
[32] Millington R J. Gas Diffusion in Porous Media [J]. Science, 1959,130(3367):100-102.
[33] Kim J, Corapcioglu M Y. Modeling dissolution and volatilization of LNAPL sources migrating on the groundwater table [J]. Journal of Contaminant Hydrology, 2003,65(1):137–158.
Multi-field coupling simulation of LNAPL migration in cold regions.
FUXiao-qin,SHI Xiao-qing*, JIANGJian-guo, WU Ji-chun
(Key Laboratory of Surficial Geochemistry of Ministry of Education, School of Earth Sciences and Engineering, Nanjing University, Nanjing 210023, China)., 2022,42(3):1346~1358
A multi-field coupling model of temperature, flow and chemical fields including water, gas, NAPL, and solid (ice) phases was established to quantitatively simulate the migration and distribution of LNAPL under freezing condition during LNAPL leakage. By comparing the LNAPL flow model under non-freezing conditions, the simulated results found that LNAPL would undergo different migration behavior due to the formed ice under freezing conditions. The formed ice prevented LNAPL from infiltrating and generated freezing potential to make LNAPL migrate to the surface. The difference of LNAPL mass flux was -51.1% when the LNAPL infiltration reached stable under freezing/non-freezing conditions. Under freezing conditions, the speed of LNAPL plume in the horizontal direction was greater than that under non-freezing conditions. The maximum predicted error of LNAPL dissolved and volatilized components during the infiltration process was 2.4% and -24.9%, respectively, if freezing condition was not considered. However, the freezing condition had little effect on the dissolved and volatilized components of LNAPL when the LNAPL infiltration reached stable, and only the volatilized component had an error of 1.8%. But the adsorbed component was reduced, and the error was -6.6%.
light non-aqueous fluid (LNAPL);multi-field multi-phase coupling;freezing potential;solute transport
X131
A
1000-6923(2022)03-1346-13
扶晓琴(1999-),女,湖南娄底人,南京大学硕士研究生,主要从事地下水动力及溶质运移方面研究.
2021-08-06
国家自然科学基金资助重点项目(41730856);国家自然科学基金资助项目(41977157)
*责任作者, 教授, shixq@nju.edu.cn
