基于钢轨吸振器的多模态复合式俘能器性能研究

2022-03-29钱韦吉雍胜杰西南石油大学机电工程学院成都610500

中国机械工程 2022年6期

钱韦吉雍胜杰西南石油大学机电工程学院，成都，610500

0 引言

轨道交通是我国重要的交通形式之一，截至2018年，我国的铁路营运里程达12.7万公里，其中高速铁路的运营里程达2.5万公里，占世界高速铁路运营总里程的60%以上。随着微机电系统技术的快速发展[1-2]，许多学者提出回收轨道振动能量，代替传统的蓄电池为低能耗的轨旁设备供电，以期减轻化学蓄电池导致的环境污染以及轨道高频振动导致的噪声污染。回收轨道振动能量，为轨道监测设备提供一种建设成本低、维护简便的供能方式，在如今轨道运输如此庞大的基数下，将具有巨大的应用潜力与研究价值，对推动我国铁路建设事业的蓬勃发展起到积极作用。

目前，国内外研究人员对轨道振动能量采集的研究比较少。杨沥等[3]提出一种轨道板垂向振动能量采集方案，通过两自由度压电式轨板振动采集器，收集到的振动能量可以通过储能装置储存，有望对轨旁设备进行间歇供电。张梅[4]在钢轨扣件部使用磁致伸缩材料安装了电磁式俘能装置，进行钢轨振动能量转换。当车辆经过能量回收路段时，扣件部受到负载导致磁致伸缩材料发生形变，进而改变了该材料的磁化强度，使感应线圈的磁通量改变，然后通过外接电路将线圈中感应电动势收集起来。为了验证该装置的可行性，通过仿真测试和实验样机计算得到137 J日均收集能量，可以满足无线传感器的供电需求。POURGHODRAT等[5]对几种轨道能量收集方式进行了验证，发现电磁式的间接振动能量收集方式对轨道能量收集研究具有极大的推动作用，该装置通过能量传动板转换列车经过该路段时的部分振动能量，带动永磁铁间的线圈垂向振动，进而在感应线圈中产生一定量的电动势，实验结果表明，当满载列车以21 km/h通过时，装置的输出功率约为2 mW。由于相关领域的研究者对采集轨道振动能量的研究并不成熟，因此，上述研究中安装在钢轨、扣件和枕木上的俘能装置受到收集时限、振动幅值等限制，能量收集效率并不理想。

1 理论分析模型和研究方法

1.1 车轮-钢轨-吸振器摩擦耦合自激振动模型

文献[6-8]研究发现，钢轨吸振器能吸收大量的振动能量，且具有振动周期相对固定、振幅较大以及振动时间相对较长的特点，是一种理想的振动能量来源，钢轨吸振器的安装位置与结构如图1所示。笔者设计了一种将钢轨吸振器和多模态压电-电磁复合式俘能装置相结合的复合吸振器。

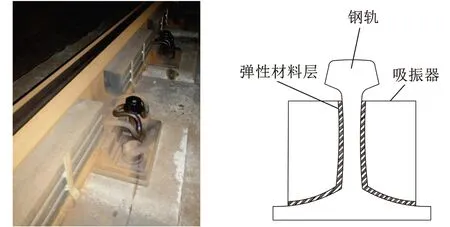
(a)钢轨吸振器安装位置(b)钢轨吸振器结构图

列车的加速、减速或弯道区段是列车行驶的重点监测区域。列车在通过这些区段时，轮轨间的蠕滑力往往是饱和的。摩擦自激振动理论[9-10]认为轮轨间的饱和蠕滑力会导致轮轨系统失稳，从而产生自激振动，因此，本文以摩擦自激振动理论为基础，使用ANSYS Workbench建立了直线加速路段上，单轮对的车轮-钢轨-吸振器摩擦耦合自激振动有限元模型，如图2a所示。当列车加速通过直线路段时，轮对受到的横向力和横向位移非常小，轮对的自旋运动也很微弱，因此，为了简化轮轨接触模型，提高计算效率，本文不考虑车轮的自旋蠕滑与横向蠕滑，并假设左右车轮的接触状态和受力状况一致，且轨面纵向蠕滑力均达到了饱和状态，即蠕滑力等于轮轨间法向接触力乘以摩擦因数。在有限元模型中，钢轨长36 m，型号为60 kg/m，钢轨吸振器尺寸为425 mm×45 mm×90 mm，接触面摩擦因系数为0.4，车轮直径840 mm，轮对的平均运行速度为45 rad/s，加速度为1.2 m/s2,行驶了0.25 s，此时，轮轨系统主要受到轴箱的垂向支撑力Fn=200 kN。边界条件以及主要参数设置如下：将接地弹簧单元建立在枕木底面以模拟道床的支撑，弹簧-阻尼单元建立在钢轨和枕木接触面以模拟扣件的作用(图2b)，在吸振器和钢轨的接触面用弹簧-阻尼单元来模拟弹性材料层(图2c)。建模参数为深圳地铁一号线现场实测数据，材料参数如表1所示，连接参数如表2所示。

(a)轮-轨-吸振器有限元模型

(b)轮轨接触单元 (c)吸振器接触单元

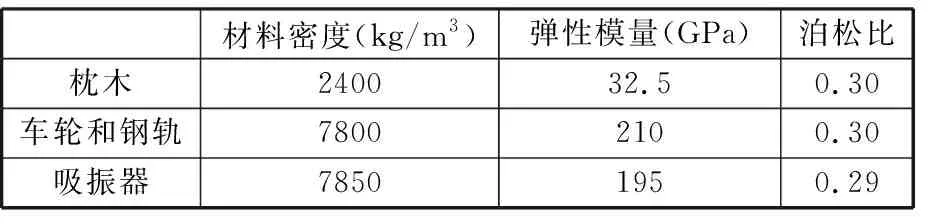
表1 轮轨模型的材料参数

表2 轮轨模型的连接参数

本文使用Hypermesh软件在轮轨接触面细化网格建立过渡单元，减小网格质量造成的结果误差(图3)。其中车轮有40 478个节点和32 416个六面体单元，钢轨有293 692个节点和184 350个六面体单元，枕木有22 419个节点和13 256个六面体单元。目前，摩擦自激振动有限元分析法包括复模态分析法和瞬时动态分析法，详见文献[11-12]。

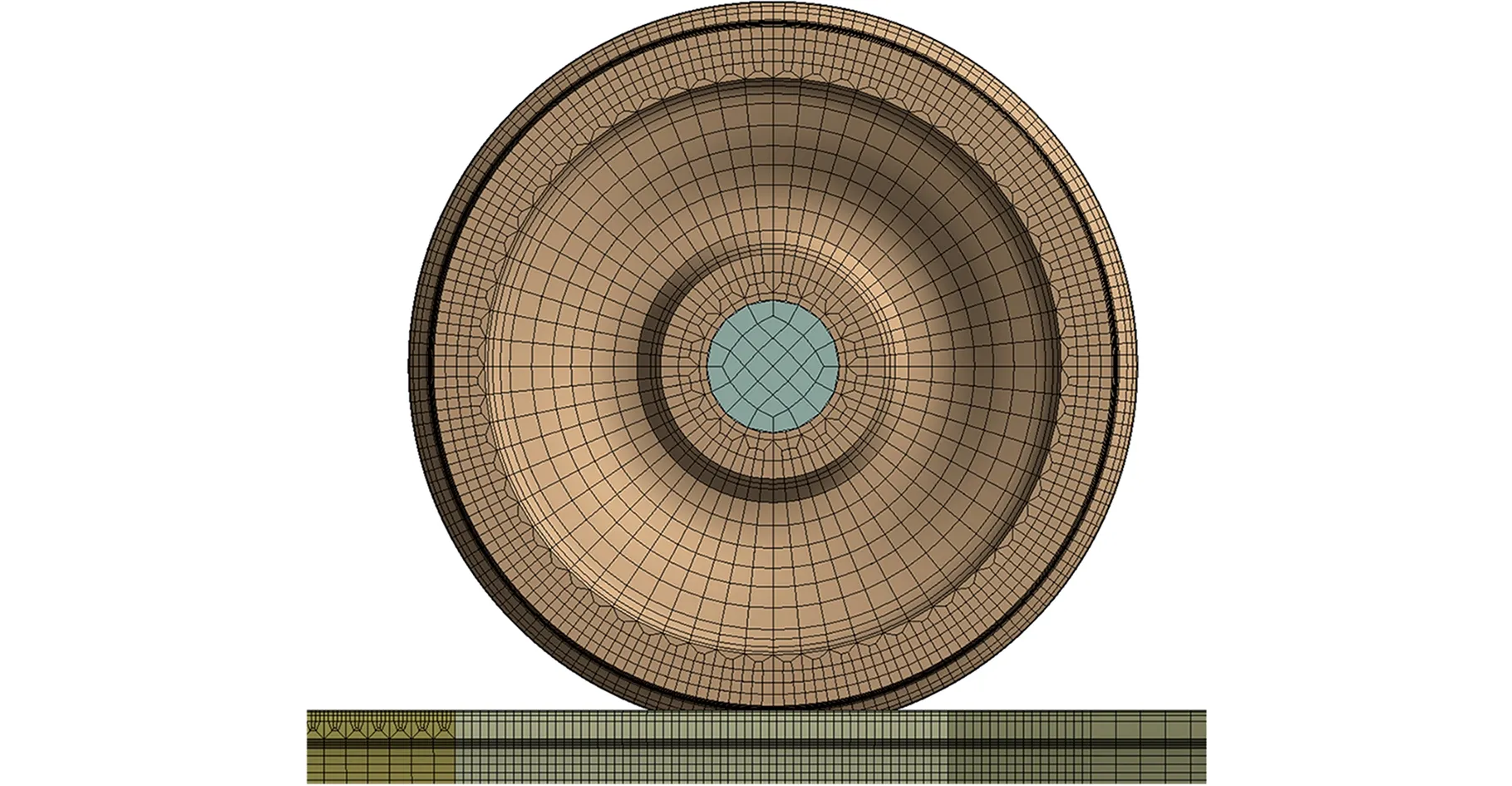
图3 轮-轨-吸振器模型细化网格Fig.3 Wheel-rail-vibration absorber model refining mesh

1.2 复合吸振器振动能量采集模型

本文以钢轨吸振器作为振动能量源，在此基础上扩展复合式俘能模块，该模块包含压电式俘能器与电磁式俘能器两部分，如图4所示。其中，螺旋型悬臂梁与压电陶瓷片组成了压电式俘能模块，永磁铁块与线圈构成了电磁式俘能模块，如图4b所示。为了准确传递钢轨振动的瞬间激励，吸振器和悬臂梁末端耦合面首先进行固定(图4a)，然后悬臂梁与磁铁块和压电陶瓷的接触面相互粘接(图4c)，其建模参数如表3所示。列车经过能量回收路段时，多模态复合式俘能装置会受到钢轨吸振器传递的外界激励，永磁铁作为质量块带动悬臂梁发生振动，同时在线圈之间做切割磁感线运动，电磁感应效应会使线圈内产生感应电流。粘贴在悬臂梁上的压电陶瓷随振动激励发生形变，利用压电材料特有的压电效应，在其表面也会产生交变电压。通过回收电路可以收集振动能量转换的电能。在计算复合式俘能模块总功率时，需要考虑压电-电磁耦合作用[13-14]对俘能效率的影响。

(a)多模态复合式俘能模块安装位置

表3 轨道振动能量采集模型的材料参数

由于轨道振动具有宽频激励的特点，故本文采用螺旋型悬臂梁结构进行振动能量回收，可以拓宽回收振动能量的频率响应范围，进而提高振动能量的收集效率[15]。

2 轨道振动能量回收装置俘能原理

2.1 俘能模块压电效应

将压电耦合模型进行简化，将螺旋型悬臂梁结构看作多段单悬臂梁(图5)，单块悬臂梁的输出功率计算方法如下。

图5 悬臂梁结构简图Fig.5 Structural diagram of cantilever beam

该结构的悬臂梁在外力作用下，自由端会发生垂直方向的弯曲变形，此时负载在悬臂梁上的PZT压电片极化方向为厚度极化，压电材料发生形变的外力方向与电极方向垂直。上述压电陶瓷片的耦合工作模式[16]为d31模式，其共振频率更低，产生的能量也比d33模式多。

正压电效应：

(1)

逆压电效应：

(2)

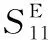
在外力F作用下，压电模块输出的开路电压

(3)

式中，tp为压电层厚度；ζstr为平均应力。

压电部分的等效电路模型如图6所示。压电陶瓷可以等效为电压源、电容Cs与电阻Rs的串联，由于压电陶瓷的电解质因数很小，所以等效电阻可以忽略不计。

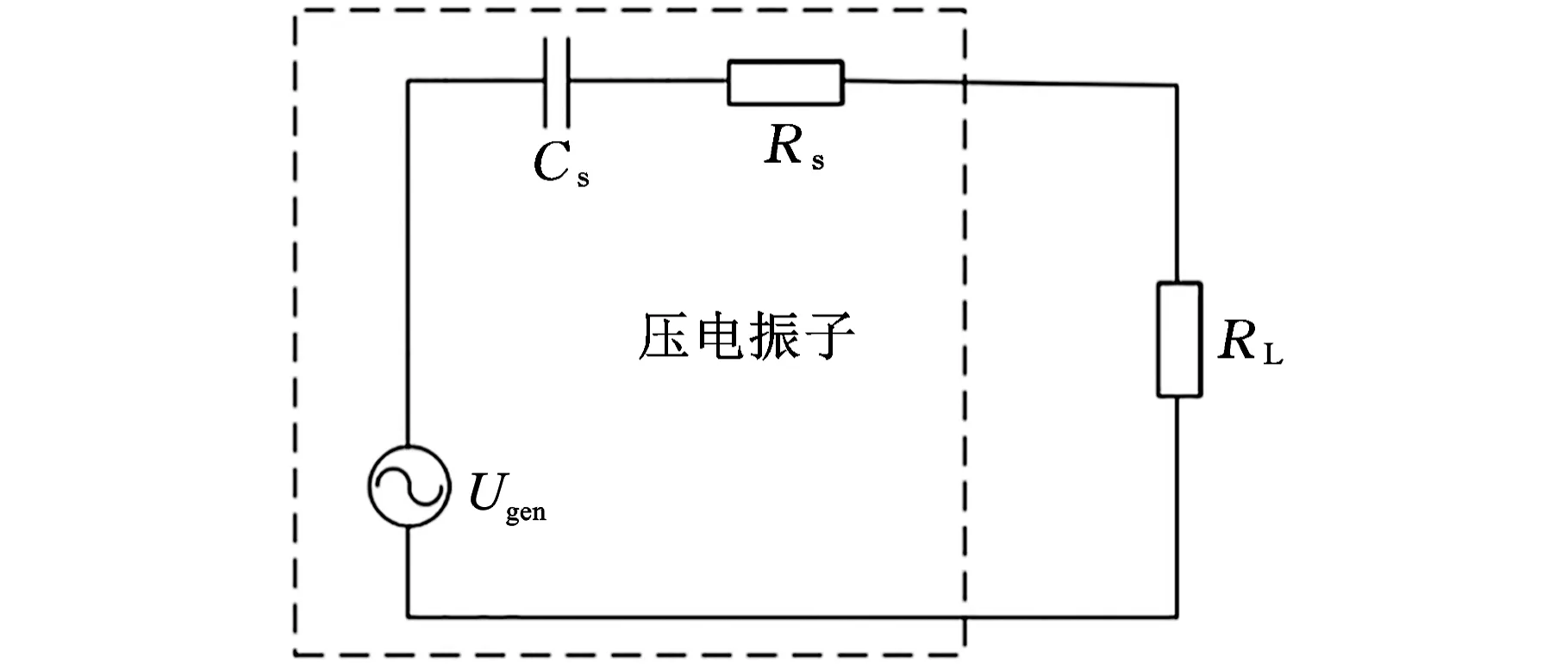
图6 压电模块等效电路Fig.6 Piezoelectric module equivalent circuit

压电陶瓷等效电容的容抗

Xcs=1/(2πfCs)

(4)

式中，f为电压源频率；Cs为等效电容。

外界负载两端电压

(5)

式中，RL为外界负载电阻；Ugen为压电片电压。

由以上公式可知，外界负载消耗的平均功率为

(6)

式中，t为时间。

2.2 俘能模块电磁感应

电磁俘能模块的永磁铁安装在螺旋型悬臂梁末端，并且在永磁铁的垂直方向对称固定了两圈800匝的线圈，如图7所示。当电磁俘能模块受到外界激励时，磁铁上下振动，导致线圈内磁通量发生变化，产生感应电动势：

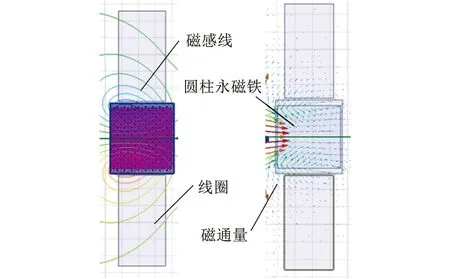
图7 电磁感应结构简图Fig.7 Structural diagram of electromagnetic induction

(7)

式中,φ为通过线圈磁通量；Ue为线圈电动势;L为线圈切割磁感线的有效长度；B为磁感应强度；z(t)为永磁铁和线圈的相对位移；N为线圈匝数。

电磁模块的等效电路模型如图8所示，其中线圈内阻Rcoil和外接负载RL是耗能原件，等效电路线圈的感抗很小，所以忽略不计，因此该模块消耗的总功率

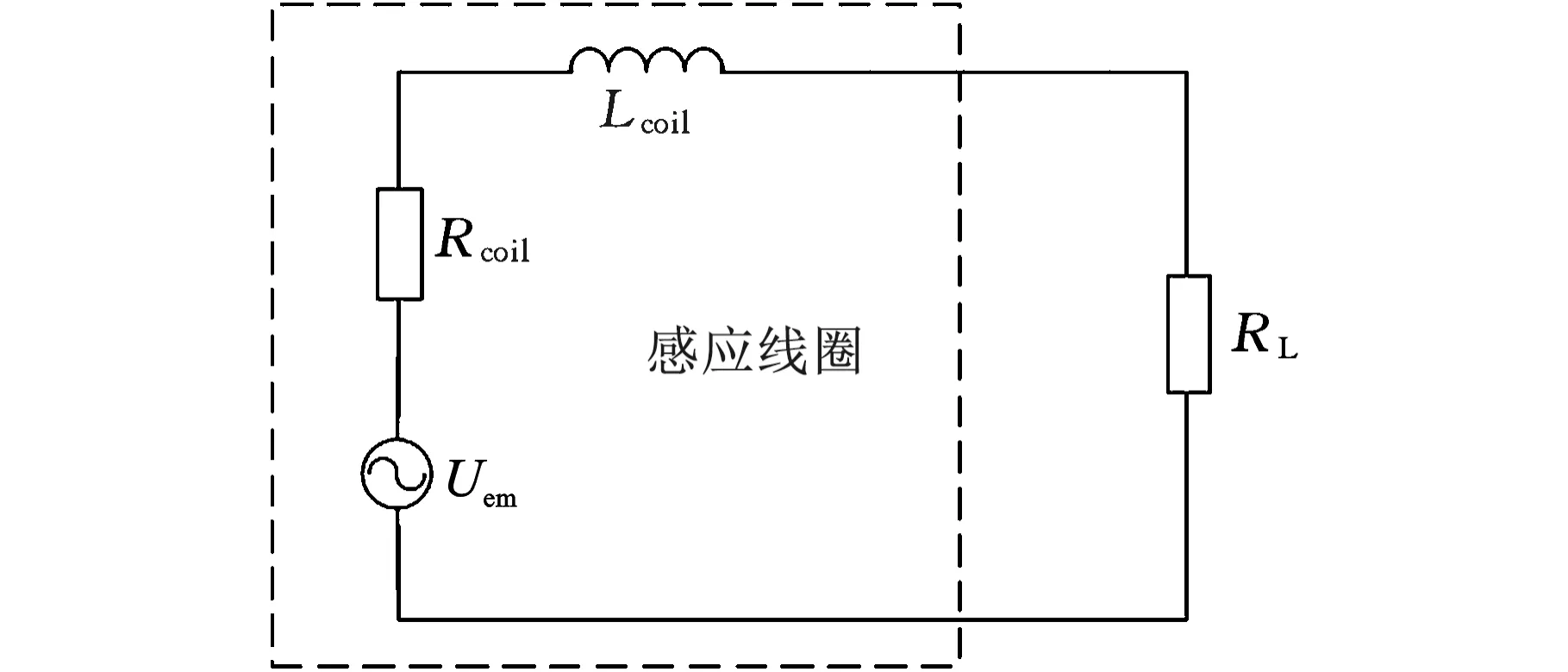
图8 电磁模块等效电路Fig.8 Electromagnetic module equivalent circuit

(8)

式中，ω为感抗；Z为等效阻抗。

去除电磁俘能模块自身消耗的功率，实际的输出功率为外接电阻RL上的有效功率，即

(9)

式中，P2为总功率。

2.3 俘能模块压电-电磁耦合效应

计算压电-电磁复合式俘能模块的总功率需要考虑压电效应和电磁感应的耦合作用。首先需要求出单一电磁模块的系统等效电磁阻尼

(10)

式中，R为电磁模块电阻。

将等效电磁阻尼施加到永磁铁上，重新计算压电俘能部分的输出功率和磁铁的动态响应，将动态响应中的速度响应作为电磁俘能部分的激励载荷，计算随激励变化的输出功率。最后将两部分的输出功率叠加，即为耦合作用下的多模态复合式轨道振动能量回收装置的总功率。

由式(6)、式(9)可知，复合式俘能模块的输出功率与悬臂梁、压电陶瓷片、永磁铁结构参数有关，选择恰当的参数可以提高输出功率。

3 分析结果与讨论

3.1 轮轨系统振动特性的现场实测

为了验证轮轨系统有限元模型的可靠性，以及摩擦自激有限元分析法预测结果的准确性，本文首先通过现场实验，在深圳地铁一号线采集了直线加速路段列车行驶的实测振动数据，分别测量了有吸振器和无吸振器时钢轨的振动响应。在测试过程中加速度测量计被垂直和横向安装在轨道底部，测量点位于两枕木跨中(图9a)。如图9b所示，每个加速度计都与电荷放大器相连，电荷放大器可以测量频率为1～15 000 Hz的0～1000g加速度信号。轨道振动实测数据(垂向)如图10 所示，图10a、图10b所示分别为安装吸振器前后的测试数据，安装前后轨面垂向加速度幅值的均方根分别为48.2 m/s2和30.9 m/s2，轨面垂向加速波动强度有明显差别。图10c所示为安装钢轨吸振器前现场测试数据的功率谱密度(PSD)分析结果，由此可知，安装吸振器前轮轨系统容易发生频率为398.5 Hz的振动。

(a)垂直加速度和横向 (b)加速度测量计位置加速度测量计安装示意图

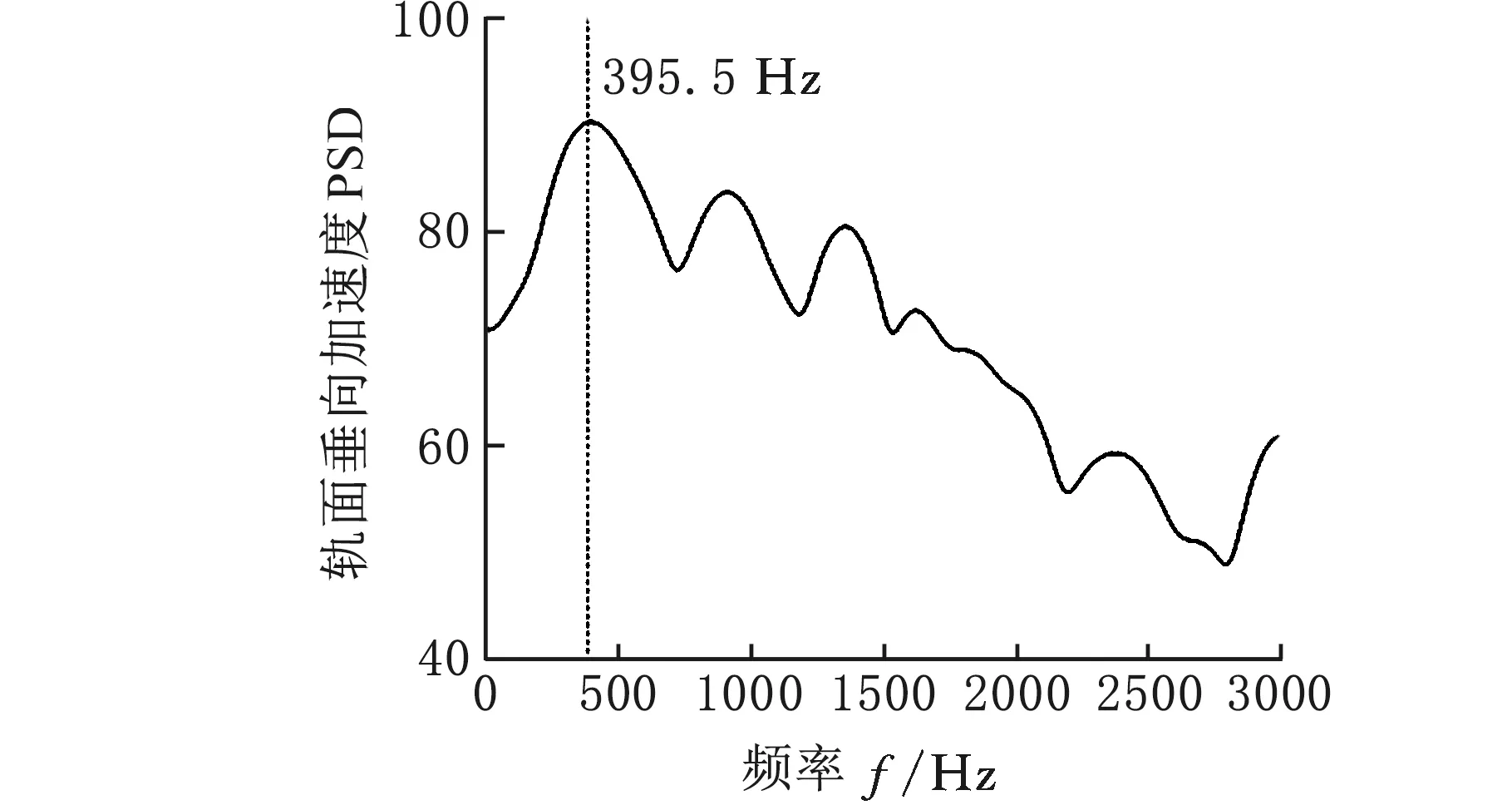
(c)安装吸振器前加速度PSD分析

3.2 带俘能模块的钢轨吸振器减振性能分析以及结果验证

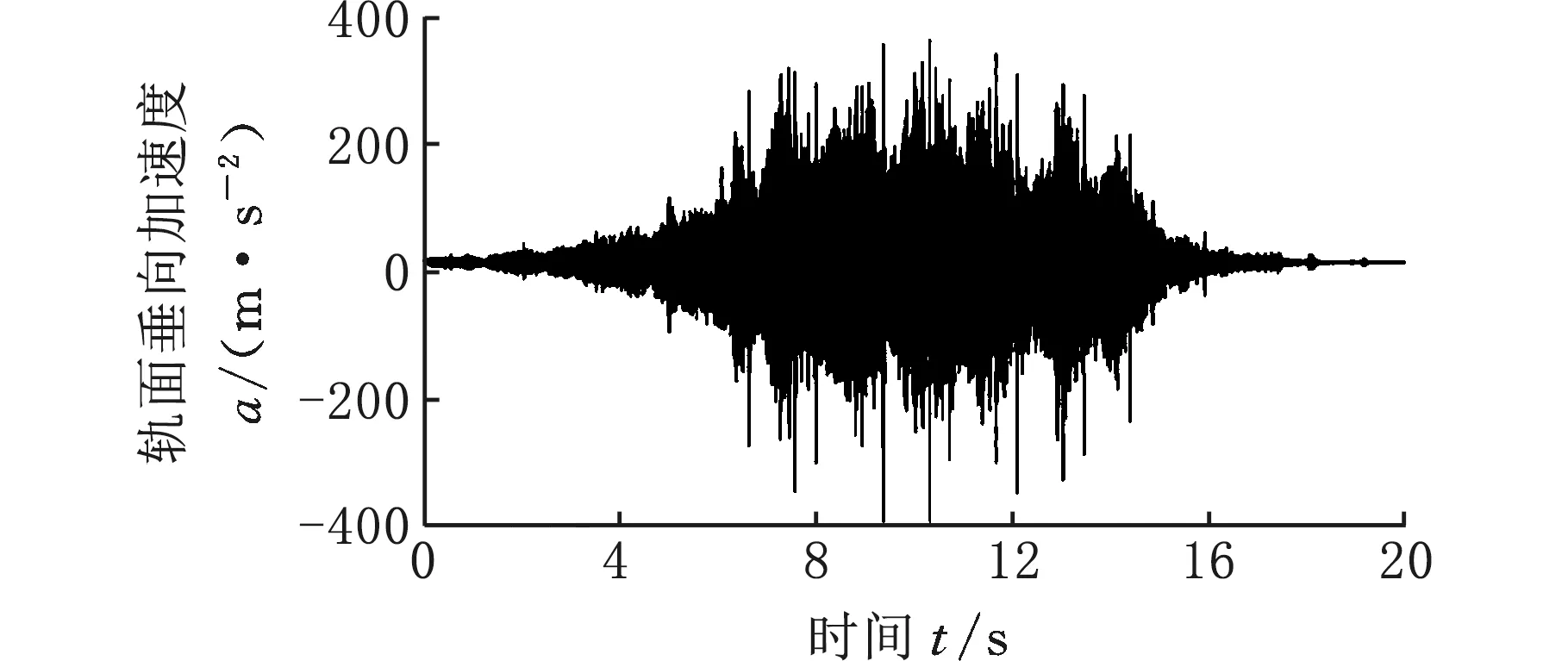
(a)安装吸振器前轨面垂向加速度

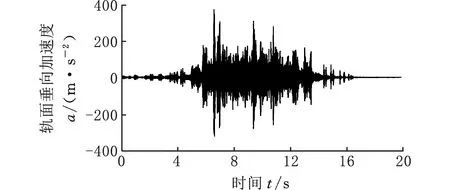
(b)安装吸振器后轨面垂向加速度

摩擦自激振动复特征值法作为研究摩擦系统频域稳定性的有效方法，已经被大多数学者认可，因此本文对车轮-钢轨-吸振器模型进行了复特征值分析，在复特征值分析结果中，模态不稳定系数[17]越大，轮轨系统越可能发生剧烈的自激振动。图11所示为安装钢轨吸振器前后轮轨系统的模态不稳定系数的变化情况，可以发现，在安装钢轨吸振器前，轮轨系统模态不稳定系数最大为0.006 12，最不稳定振动频率为404 Hz。该现象与同工况下的深圳地铁一号线车辆加速区段实测的轮轨系统波磨形成频率[18]395.5 Hz(图10c)相近，说明该模型能准确预测轮轨系统不稳定自激振动的发生频段。在安装钢轨吸振器和扩展复合式俘能模块后，轮轨系统0～600 Hz范围内的模态不稳定系数均明显减小，即安装钢轨吸振器能有效抑制轮轨系统的不稳定自激振动,并且在扩展复合式俘能模块后系统的模态不稳定系数并未明显增大，由此可知，复合式俘能模块不会显著影响钢轨吸振器的减振性能，保证了钢轨吸振器的减振效果。图12所示为该轮轨系统在频率所示为404 Hz时的摩擦自激振动模态振型，可以看出不稳定振动发生在车轮与钢轨的接触面，进一步验证了轮轨接触面的蠕滑力处于饱和状态时会引起轮轨系统发生不稳定摩擦自激振动。

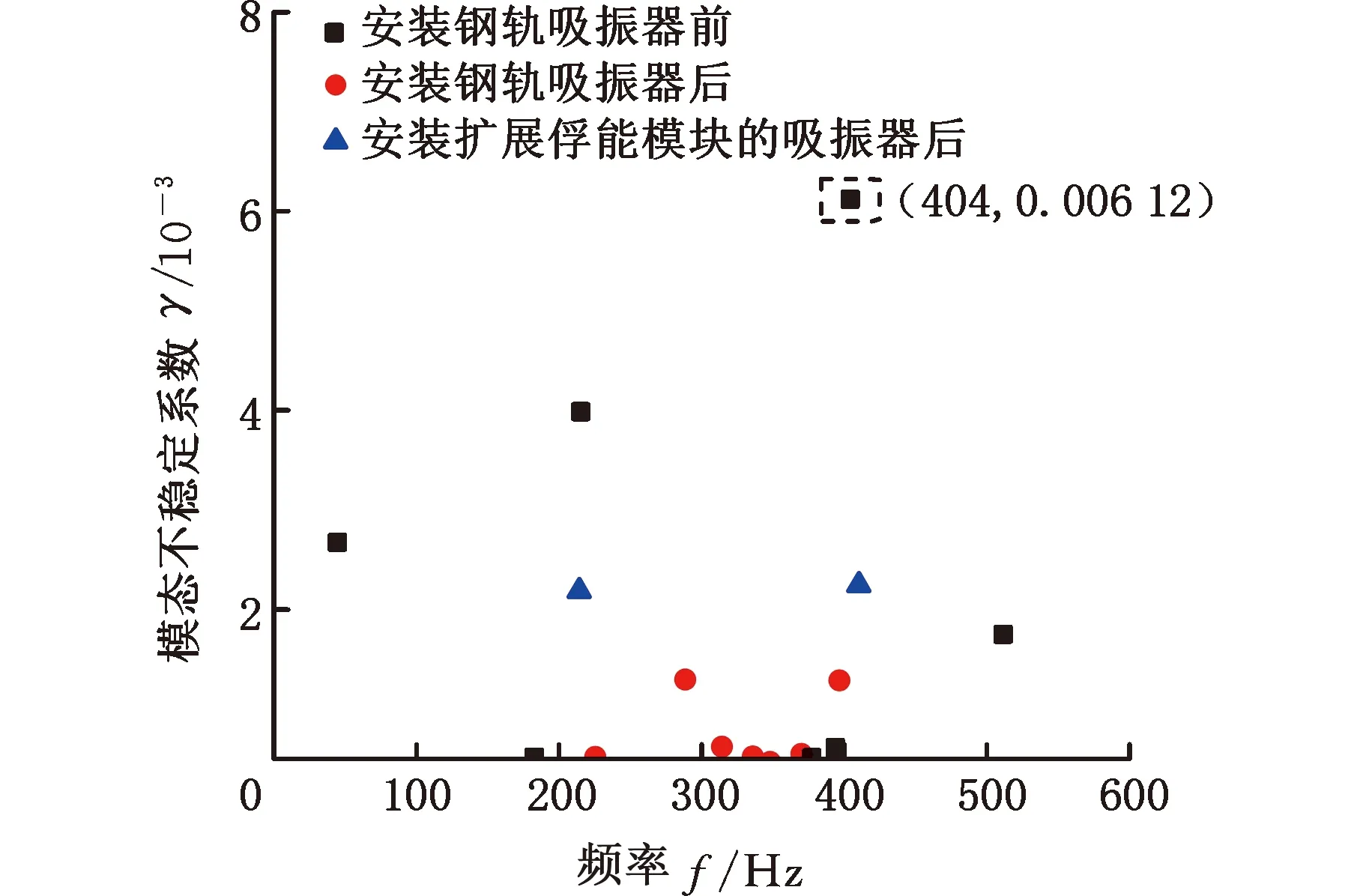
图11 复特征值结果Fig.11 Complex eigenvalue results

图12 γ=0.006 12,f=404 Hz的摩擦自激振动模态振型Fig.12 The mode shape of friction self-excitedvibration with γ=0.006 12,f=404 Hz

研究多模态复合式俘能模块的发电性能时需要使用轮轨系统不稳定振动的时域信号作为输入载荷,因此，本文使用瞬时动态分析法预测了轮轨系统发生不稳定振动的时域变化情况,并且，通过对深圳地铁一号线轮轨系统时域结果(图10a和图10b)进行对比分析，证明了该轮轨系统振动分析模型的准确性和可靠性。

图13和图14为轨面垂向加速度和法向接触力在摩擦因数为0和0.4时的时域变化曲线，除轴箱垂向支撑力之外，不再添加其他的外部激励。可以发现，轨面垂向加速度与轮轨接触力在摩擦因数为0.4时出现了剧烈波动，说明轮轨间的饱和蠕滑力会导致轮轨系统的自激振动。安装钢轨吸振器后，轨面监测点的垂向加速度幅值显著减小(图15a)，由此可知，该段钢轨的轨腰两侧安装的钢轨吸振器对轨道振动减振效果明显，这一现象与3.1节现场实测结果一致。对比图15a与图15b可以发现，吸振器扩展复合式俘能模块后，在0.13～0.15 s轨面垂向振动略有增大。这可能是添加复合式俘能模块后，压电-电磁之间的耦合作用等效增大了钢轨吸振器的结构质量和刚度，从而对钢轨吸振器的减振性能造成了一定影响。

图13 轨面垂向加速度Fig.13 Vertical acceleration of rail surface

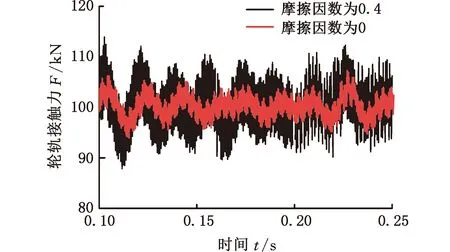
图14 轮轨接触力Fig.14 Wheel rail contact force

(a)安装吸振器前后轨面垂向加速度

综上所述，该模型的预测结果具有较高的准确性，为下文对俘能模块发电性能的分析提供了可靠的时域数据。

3.3 多模态复合式俘能模块的发电性能分析及结果验证

3.3.1俘能模块数值分析模型的可靠性验证

根据文献[19]的实验数据，得到图16a所示双盘单悬臂梁系统摩擦过程中示波器记录的俘能电压信号通过快速傅里叶变换(FFT)后的频域图，图16b所示为同工况下采用摩擦自激振动理论建立的仿真模型对电压信号的预测结果。可以发现，摩擦系统实测振动电压信号的主振频率为316 Hz，与有限元模型预测的振动频率320 Hz非常接近。值得注意的是，由于有限元模型没有考虑黏滑行为，因此仿真结果显示的是连续振动的电压信号，这与试验中显示的间歇间断信号略有不同。综上可知，采用摩擦自激振动理论所建立的数值模型能较好地反映摩擦俘能系统的动态特性和输出电压特性，具有可行性。图16c为俘能模块的电压信号FFT频域图，由于螺旋型悬臂梁具有多臂不同频共振的特点，该俘能模块在该频段存在6个波峰，与文献[19]的单悬臂梁结构单频俘能特性对比发现，本文俘能模型符合实际工况，能有效拓展振动能量俘能频带，提高能量采集效率。

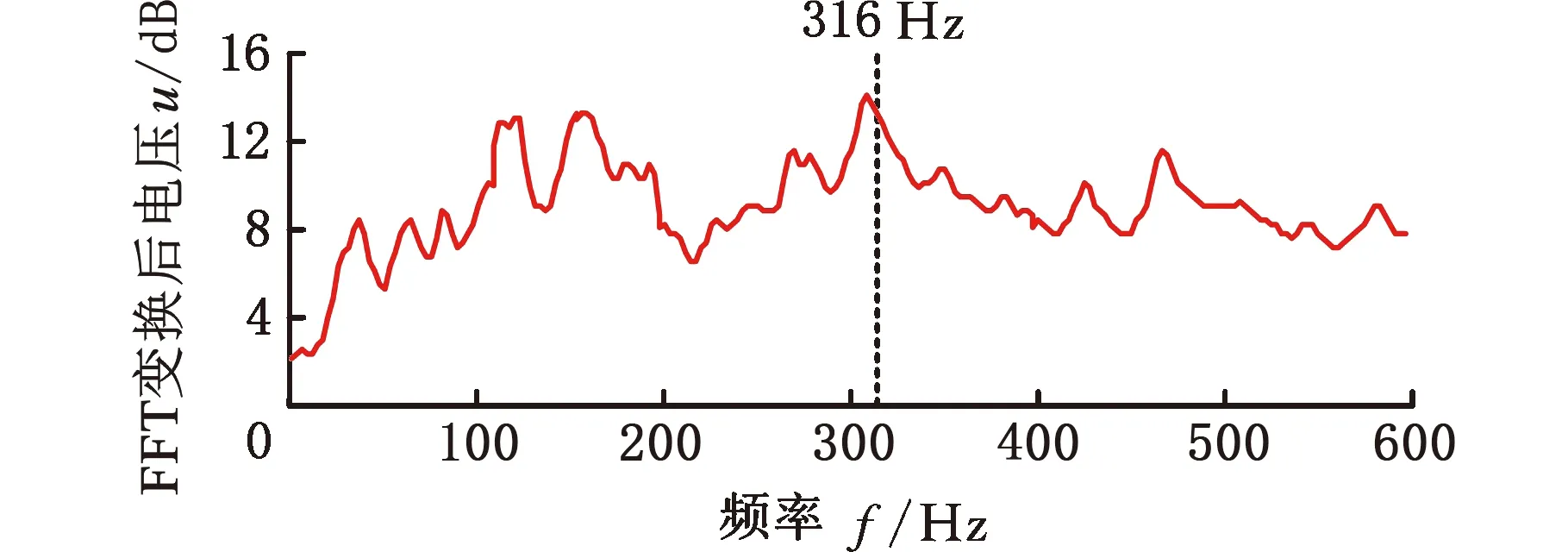
(a)单悬臂梁垂向电压信号FFT实测数据

3.3.2单一压电式和电磁式俘能模块的发电性能分析

车轮-钢轨-吸振器系统的瞬态分析结果显示，当轮轨系统发生不稳定振动时，钢轨吸振器的垂向振动较大，其他方向的振动幅度可以忽略不计。因此，使用Workbench进行谐响应分析时，选取钢轨吸振器与俘能模块之间的耦合面的垂向振动位移作为谐响应简谐载荷,将其作用于悬臂梁起始端约束节点，计算多模态复合俘能模块单一压电部分的输出功率。同时，为了得到单一电磁部分输出功率，将位于悬臂梁末端的永磁铁块的振动位移和振动加速度作为电磁俘能模块的激励源，使用Maxwell软件进行电磁场瞬态分析。单一压电和单一电磁俘能模块的发电性能分析结果如图17和图18所示。对比可以发现，单一压电模块的最大输出功率是电磁模块的最大输出功率的6倍，这是因为轮轨间的的摩擦自激振动属于微米量级的弹性振动，导致永磁铁和线圈的相对位移非常小,因此，电磁模块的振动能量转换效率远小于压电模块。图19是压电俘能模块永磁铁的位移频域图，可以发现频率为30 Hz、61 Hz、158 Hz、219 Hz和345 Hz时，压电俘能模块的输出功率与位移幅值都处于波峰位置，这说明压电俘能系统发生共振时俘能效率最高。

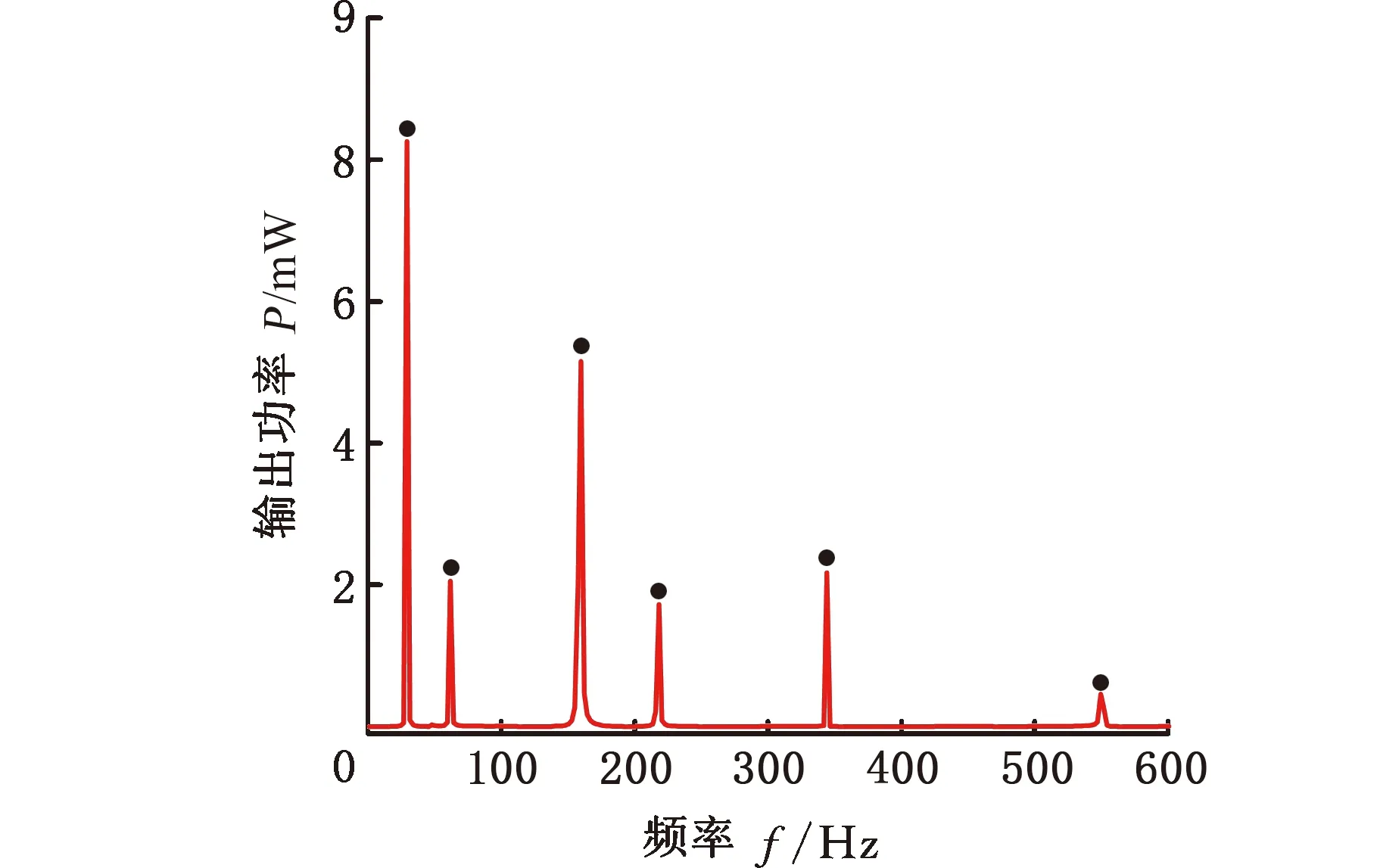
图17 压电俘能模块输出功率Fig.17 Output power of piezoelectric energy harvesting module

图18 电磁俘能模块输出功率Fig.18 Output power of electromagnetic energy harvesting module

图19 永磁铁位移频域信号Fig.19 Frequency domain signal of permanent magnet displacement

3.3.3压电-电磁耦合作用下复合式俘能模块的发电性能分析

计算复合式俘能模块的总功率需要考虑压电效应和磁计算感应之间的相互影响，因为两种能量转换之间存在耦合作用。通过式(10)可以计算得到等效电磁阻尼，将其加载在永磁铁上再次进行压电模块谐响应分析，可得到压电-电磁耦合作用下复合式俘能模块压电部分的输出功率。然后，将永磁铁的位移激励和速度激励(加载等效电磁阻尼的条件下)代入Maxwell进行电磁场瞬态分析，即可得到耦合后的电磁部分输出功率。在结构与振动输入相同的条件下，耦合电磁阻尼以后，复合式俘能器压电部分的输出功率相对于单一的压电式俘能器的输出功率减小了16.9%，如图20所示；复合式俘能器电磁部分的输出功率相对于单一的电磁俘能器的输出功率减小了19.2%，如图21所示。这是由于复合式俘能模块中安培力转换的等效电磁阻尼消耗了部分钢轨振动能量。相对单一俘能方式，复合式俘能模块的最大输出功率达8.78 mW，是单一压电式俘能功率的108.2%，是单一电磁式俘能功率的469.5%，如图22所示。这说明采用多模态复合式俘能装置可以有效提高振动能量的收集效率以及拓宽俘能频带。

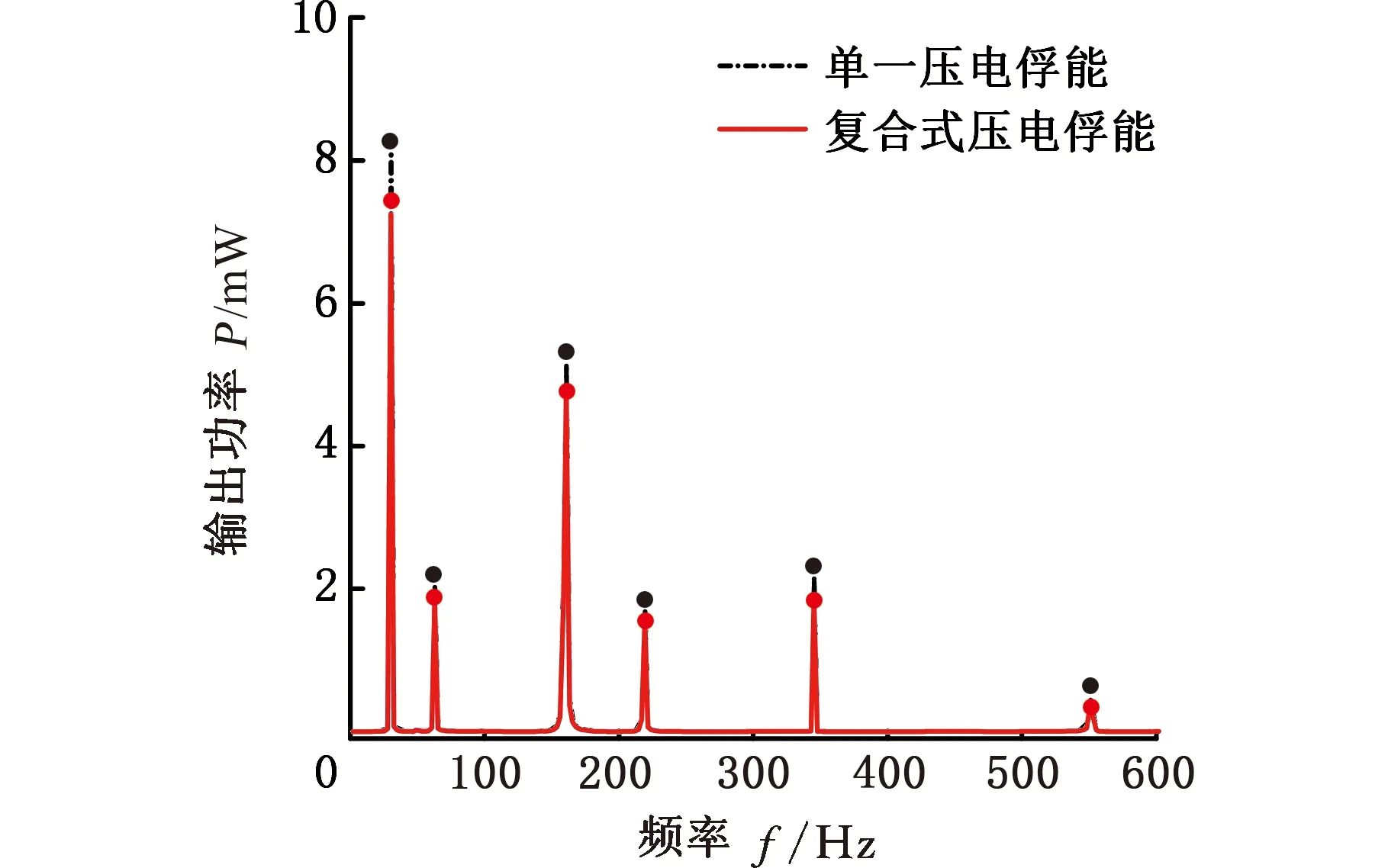
图20 复合式压电俘能功率Fig.20 Compound piezoelectric energy harvesting power

图21 复合式电磁俘能功率Fig.21 Compound electromagnetic energy harvesting power

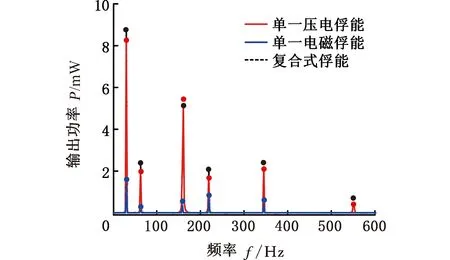
图22 复合式总功率和单一式输出功率Fig.22 Compound total power and single output power

为了验证钢轨吸振器作为振动能量源的可靠性和俘能优势，笔者在同一路段位置上，分别在钢轨吸振器、钢轨、扣件和枕木上设置振动测试点，获取振动位移，并将振动位移作为激励条件，分别作用于复合式俘能模块。俘能模块输出电压的瞬时动态分析结果如图23所示。可以看出，当以钢轨吸振器的振动位移作为激励条件时，俘能模块的输出电压幅值波动最大；以钢轨和扣件的振动位移作为激励条件时，输出电压的波动大幅减小。为了保证列车安全运行，枕木受到的约束力最多，因此在其振动位移激励下的俘能电压最小。

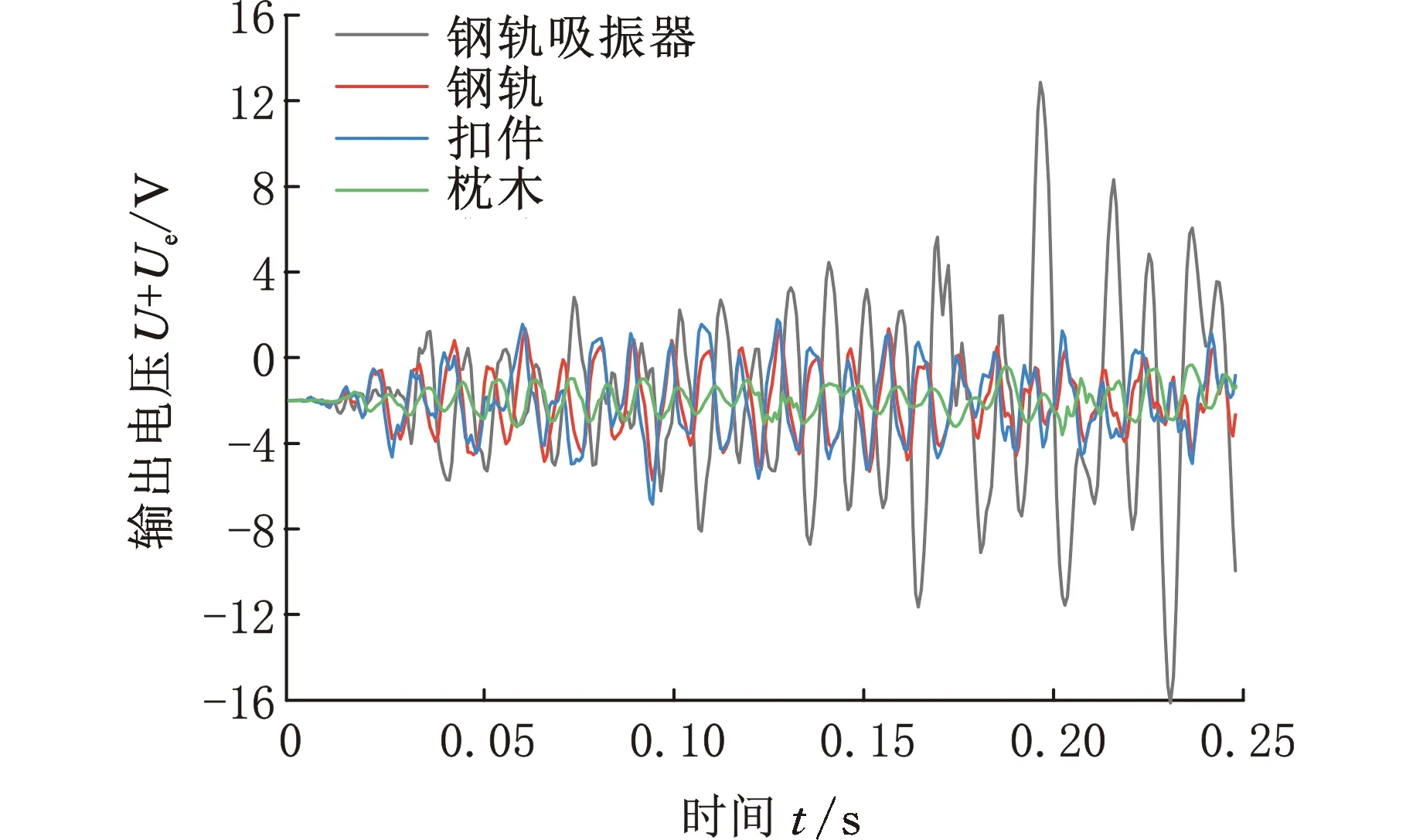
图23 俘能模块输出电压时域信号Fig.23 Energy harvesting module output voltagetime domain signal

轨道振动能量的产生主要集中于列车经过的瞬间。由图23可以看出，列车快速经过后，在钢轨、扣件和枕木的振动位移激励下，俘能器的输出电压平缓下降。但是，以钢轨吸振器的振动位移作为激励条件时，俘能器的输出电压仍能保持幅值，并有逐渐增大的趋势。这是由于在列车通过时钢轨吸振器吸收了大量的轨道振动能量，并通过自身的持续振动使振动能量发散。这一分析结果验证了钢轨吸振器具有振幅较大以及持续振动时间相对较长的特点。

目前，常用的低能耗轨旁设备需要的工作电压为1.8～3.8 V，本文设计的俘能模块的最大输出电压接近16 V，完全满足供能需求。

3.4 俘能模块结构参数对发电性能的影响

当俘能模块受到钢轨吸振器传递的振动激励时，负载在悬臂梁上的压电陶瓷片会发生形变，同时线圈间的永磁铁上下振动切割磁感线。根据压电片形变发电的特性以及电磁感应现象的特点，可以通过提高俘能模块应变能的方式提高俘能效率。因此，本文对该模块的螺旋悬臂梁、压电陶瓷片以及圆柱永磁铁进行了参数化分析，在保证俘能模块正常运行的同时，研究结构参数对俘能效率的影响。

在俘能模块材料参数不变的前提下，分析了压电片结构参数对压电部分俘能效率的影响，如图24所示。可以发现，增大压电片的厚度(图24a)、减小压电片的宽度(图24c)均可以有效提高压电片的输出电压。但是，随着压电片厚度和宽度逐渐增大，对输出电压的影响将逐渐减小。分析结果显示，压电片的长度为13 mm时，输出电压最大(图24b)。螺旋悬臂梁的厚度对输出电压的影响规律如图24d所示。螺旋悬臂梁的厚度在1.5 mm左右时，压电片输出电压最大。随着悬臂梁厚度增大，输出电压出现频繁波动的状况。导致这种现象的原因是，永磁铁和压电片负载在悬臂梁上增大了悬臂梁的振动惯性，当悬臂梁厚度出现微小变化时，会改变俘能模块的整体结构质量分布，影响了螺旋悬臂梁的共振模态从而出现参数共振失稳现象[20]。

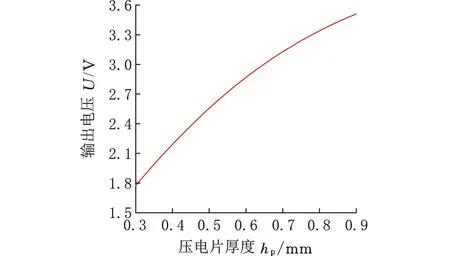
(a)压电片厚度变化

电磁部分的结构参数对俘能效率的影响规律如图25所示。随着永磁铁直径的增大，电磁模块的输出电压逐渐增大(图25b)。随着永磁铁与线圈间距离的增大，电磁模块的输出电压逐渐减小(图25a)。当改变上述两个参数时，输出电压出现了较大波动，这是因为上述结构参数的改变影响了线圈周围磁感线的分布，导致通过线圈的磁感线较为密集，反而增大了电磁感应强度，因此出现了输出电压波动。

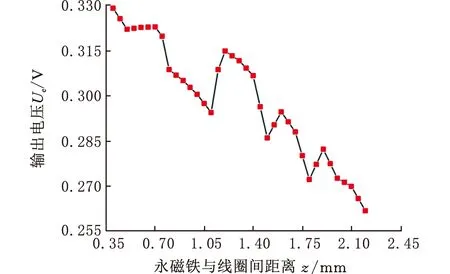
(a)永磁铁与线圈距离变化

随着线圈匝数的增加，电磁模块的输出电压逐渐增大，当线圈匝数超过600后，递增的趋势明显减缓，如图25c所示。这是因为轴向增大线圈匝数的同时也增大了线圈电阻和线圈轴向长度，距离永磁铁距离越远的线圈切割的磁感线越稀疏，产生的感应电流也相应减小。还可以看出，由于轴向增大线圈匝数不会改变磁感线的分布状态，因此没有产生波动的磁感应电动势。