基于梳状导频的通导融合测距优化配置方法

苏静芳，苏 佳*，易卿武，曾存良，杨志华，王 婷

(1.河北科技大学 信息科学与工程学院，河北 石家庄 050018；2.卫星导航装备与技术国家重点实验室，河北 石家庄 050081)

0 引言

随着全球卫星导航系统的不断发展，人们对位置服务的要求不断提高[1]。卫星导航是常用的定位方式，但在室内、复杂地理环境、电磁环境等情况下，不能很好地为大众提供定位服务[2]。如今，随着移动通信技术的发展与移动网络的建设[3]，无线通信信号在室内覆盖范围广、信号功率强的优势愈发突显，将部分通信信道传输测距信号，可以弥补导航信号在室内定位中的不足，将其优势与导航信号高精度定位能力融合，可以实现更高精度的室内外无缝定位[4-5]。

OFDM技术具有抗信道衰落、抗多径、抗干扰等能力，可以有效解决室内定位的问题。因此，对OFDM信号的测距系统进行优化配置十分重要。研究者提出了一些系列测距算法，来进一步优化系统。在测距系统中，将到达时间(Time of Arrival，TOA)估计或到达时间差(Time Difference of Arrival,TDOA)估计融入到OFDM系统，通过估计时间来进行测距[6]。文献[7]提出了时频域联合估计法，通过搜索相关峰和求信号相位差来估计时延。由于相位会受噪声影响，文献[8]提出相位补偿技术,对相位进行合理补偿，提高时延估计的精度。文献[9]和文献[10]利用子载波相位差来估计时延，有效地降低了多径对测距的影响。文献[11]提出MUSIC(Multiple Signal Classification，MUSIC)超分辨率TOA估计算法，在此基础上，文献[12]引入深度学习，进一步减小了多径影响。此外，将多入多出(Multiple-Input Multiple-Output，MIMO)与TOA、到达角度(Direction Of Arrival,DOA)或TDOA结合，通过测量接收OFDM信号的时延、时延差、到达角度差等方式来实现测距[13～15]，不断完善测距系统。

当然，改进测距算法主要为了解决测距精度的问题。随着新一代通信系统和导航系统发展[16]，提出导航与通信融合定位，因此，对测距系统提出了更高的要求，不但要求测距系统要具有高的测距精度，强的抗信道衰落、抗干扰等能力，而且要求降低通信资源占用率。为了降低通信载波占用率，在OFDM体制下，本文提出基于梳状导频的通导融合测距的优化配置方法，测距导频信号采用梳状结构，占用部分通信载波来进行测距估计，在保证测距精度的同时，不断提高通信资源利用率。

1 基于梳状导频的通导融合测距模型

1.1 传统的OFDM体制通导融合测距模型

在理想OFDM体制通导融合测距系统中，利用了OFDM信号的时频特性，发送序列通过快速傅里叶反变换(Inverse Fast Fourier Transform,IFFT)将发送端信息调制到每个不同子载波上，并生成测距信号。在时域上，通过搜索接收信号的相关峰来进行粗时延估计；在频域上，在相关峰最大的时刻对接收信号进行快速傅里叶变换(Fast Fourier Transform,FFT)变换后，通过求出相位偏移进行精时延确估计。既可以克服伪距测距带来的测距模糊问题，又可以避免相位测距带来相位模糊问题。测距系统不仅具有相关测距抗噪声干扰的特性，还具有相位测距的高精度特性，通过时频域联合处理，改善了测距模糊度问题，从而大大提高了距离估计的精度。

而在实际的OFDM系统中，由终端和基站之间相对运动带来的多普勒频率偏移会破坏子载波间的正交性，影响数据解调和对测距信号的TOA估计[17]。OFDM通信系统通常通过2个过程实现载波同步，即捕获过程和跟踪过程。捕获过程容许的频率偏移可以较大，可能是子载波间隔的若干倍；而跟踪过程会将此频率偏移缩小，通常跟踪过程之后，对频率偏移的要求大约要小于子载波间隔的1%～2%，系统产生的3 dB相位噪声带宽大约为子载波间隔的0.01%～0.1%。表1所示为各系统的多普勒频率和载波频率偏差(Carrier Frequency Offest,CFO)[18-20]。

表1 各系统的多普勒频率和载波频率偏差(CFO)

因本文主要讨论基于梳状导频的OFDM优化测距配置方法，OFDM系统中多普勒频率偏移对其影响已经得到了较好的解决。不失一般性，本文接下来的推导未考虑多普勒频移对FFT及时延估计的影响，在后续的研究中会基于旋转不变技术的信号参数估计(Estimating Signal Parameter Via Rotational Invariance Techniques,ESPRIT)算法，对梳状导频和循环前缀下多普勒频率偏移对时延估计的影响问题进行详细分析。OFDM信号测距系统框图如图1所示。

图1 OFDM信号测距系统框图Fig.1 Block diagram of OFDM signal ranging system

OFDM系统发射信号可表示为：

(1)

式中，Xi为一个OFDM符号内的第i个测距导频数据信息；N为子载波数量；T为符号持续时间。在OFDM测距系统中，将测距导频信息分配到每一个子载波上，可以有效地抑制多径等因素引起的快衰落现象。OFDM测距系统中，Xi为已知同步序列，接收端可根据发送的Xi进行系统同步及测距。

1.2 基于梳状导频的通导融合测距模型

在OFDM体制下，利用通信资源完成测距任务，但同时要减少测距信息占用的通信资源，因此，本文采用梳状结构的测距导频，对测距系统进行优化配置，即将图1中的发送序列通过快速傅里叶反变换调制到个别子载波上，再将生成的测距信号进行时频域联合估计。

测距导频采用梳状结构下的OFDM系统发射信号可表示为：

(2)

式中，X2i-1为一个OFDM符号内的第2i-1个测距导频数据信息；X2i为一个OFDM符号内的第2i个测距导频数据信息；N为子载波数量；M为导频数量,且M≤N；T为符号持续时间。采用梳状导频结构，将每一个测距导频数据信息分配给序号为奇数的子载波，其余空的子载波可传输其他通信信息。这样不仅克服了多径等环境中带来的快衰落现象，而且大大降低了通信资源占用率。

发送信号通过高斯白噪声信道，经过传输时延τ后，接收端接收到的信号表示为：

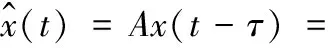
(3)

式中，A为信号经信道传输后的幅值；n(t)为高斯白噪声。

2 基于梳状导频的通导融合测距算法

2.1 时域时延估计

时域时延估计根据搜索接收信号的相关峰，可得出时域上的时延值。

在时域上，对接收信号式(3)进行采样，采样间隔为Ts=T/N，得到采样后的接收信号：

xk=x(kTs-τ)=

(4)

接收端产生的本地信号为：

(5)

式中，m为采样起始位置；τ为传输时延。

将采样信号与本地信号做自相关：

(6)

求出自相关函数R(m)的峰值，即m的取值：

n=arg{max|R(m)|}。

(7)

时域时延估计结果为：

τ1=n·Ts。

(8)

在进行时域时延估计时，考虑到采样时m的取值可以为整数或小数，为了分析不同的m取值下对时域时延估计的影响，进行了如下仿真：选取子载波为100，m整数部分取值为50，小数部分取值为0.1～0.5进行仿真，观察小数倍采样对时域时延估计的影响程度，进而确定m的小数取值范围。小数倍采样对时延估计的影响如图2所示。

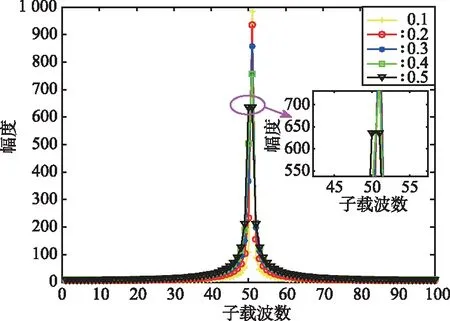
图2 小数倍采样对时延估计影响Fig.2 Impact of fractional sampling on time delay estimation

由图2可以看出，当m的小数取值为0.1～0.4时，会出现明显的相关峰，对测距导频信号的自相关性无影响。由式(6)和式(7)可知，在时域估计时，根据相关峰出现的位置，可得到整数时延估计的准确值，但小数时延估计值无法估计；当m小数部分的取值为0.5时，由图可知，相关峰不明显，导频信号的自相关性受到影响，所以，在时延估计时，无法准确估计整数估计时延值，会对整数时延估计产生误差。因此，在时域进行时延估计时，小数倍时延取值过大，会对整数倍时延估计带来误差。但是，在进行时域时延估计时，只能估计整数倍采样下的时延，小数倍时延无法估计，而小数时延估计值可通过载波相位差来得到。

2.2 频域时延估计

由于时域上只能估计整数倍时延，要更精确地估计时延值，就要估计出小数倍时延值。由于信号时延会对信号产生相位的变化，因此，小数倍的时延估可以在频域上进行。

在频域上，对接收信号式(3)进行采样，采样间隔为Ts=T/N，得到采样后的信号。采样后的接收信号表示为：

(9)

式中，i为采样点序号；τ2为频域上的小数传输时延。

Z=Y(M)·X(M)*,

(10)

(11)

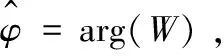
(12)

(13)

式中，L为频域相关间隔。

距离计算为：

r=c·(τ1+τ2),

(14)

式中，c为电磁波传播速度，c=3×108 m/s。

3 测距仿真结果及分析

3.1 传统通导融合测距算法仿真结果及分析

在OFDM体制下，传统通导融合测距算法仿真中，系统仿真参数如表2所示。

表2 系统仿真参数

因为频域相关间隔L影响频域估计的精度，所以要在L的不同取值情况下，进行L对测距误差影响的仿真。仿真参数如表2所示，对不同信噪比下，取不同L/N值时的测距误差进行仿真，并找出合适的L/N值。在不同信噪比下L/N取值与测距误差的关系如图3所示。

图3 L/N取值与测距误差的关系Fig.3 Relationship between L/N and ranging error

由图3可以看出，在L/N取值相同的情况下，随着信噪比降低，误差变大；在相同信噪比下，随着L/N的取值增加，测距的均方根误差上下浮动不大，基本保持一致。当然，其也会受噪声的影响，但并不影响L/N最佳值的选择。信噪比为-15 dB，当L/N的取值在0.3～0.7时，测距误差上下浮动不大，为3～4 m，此时，对测距影响最小的L/N的取值为0.51;信噪比为-10 dB，L/N的取值在0.3～0.7时测距误差最小，在1 m左右，此时，L/N的最佳取值为0.62；信噪比为-5 dB，在不同L/N的取值下，测距误差都在1 m以下，此时L/N的最佳取值为0.53。总体来说，在不同信噪比下，当L/N=0.55时，测距误差最小。所以，在进行测距仿真时，选用L/N=0.55进行仿真。

仿真参数不变，令L/N=0.55。当子载波数量N=4 096，2 048，1 024，512时，对不同子载波数在不同信噪比下测距精度进行仿真，结果如图4所示。

图4 不同载波数量下测距误差与信噪比的关系Fig.4 Relationship between ranging error and SNR under different carrier numbers

由图4可以看出，在条件相同的情况下，信噪比降低，测距误差都随之降低；信噪比相同，子载波数越大，测距精度越高。在不同信噪比下，当子载波为4 096时，测距误差最小，测距精度达到1 m。所以，为了保证测距精度，测距导频采用梳状结构进行测距时，选用子载波为4 096进行仿真。

3.2 基于梳状导频的通导融合测距算法仿真结果及分析

在OFDM体制下，传统的通导融合测距系统中，采用梳状导频对系统优化配置后，进行测距算法仿真，其仿真参数如表3所示。

表3 优化配置后，通导融合测距系统的仿真参数

测距导频信号采用梳状结构，分别插入到序号为奇数或偶数的子载波上。对测距导频数据分别为4 096，2 048，1 024，512，在不同信噪比下的测距精度进行仿真，结果如图5所示。

图5 不同导频数量下测距误差与信噪比的关系Fig.5 Relationship between ranging error and SNR for different pilot numbers

由图5可以看出，在信噪比相同的情况下，测距导频数越大时，测距精度越高，占用的子载波就越多，通信资源占用率就越高。当测距导频信息占用的子载波越少，信噪比为-5 dB时，测距精度可达到8 m以下，通信资源利用率降低。当测距导频数为2 048，OFDM信号在-5 dB的情况下，测距误差可达到0.9 m。测距精度与测距导频未采用梳状结构时基本一致，且通信资源的占用率比原来降低了一半。

测距系统进行优化配置后，采用梳状测距导频结构下进行OFDM信号测距，测距导频数分别为512，1 024，2 048，4 096，分别插入到序号为奇数或偶数的子载波上，其余空的子载波传输其他通信信息。导频数据占用子载波的比例如图6所示。

图6 导频数据占用子载波的比例Fig.6 Proportion of subcarriers occupied by pilot data

当采样起始位置m=1 000，小数时延τ2=0.02 μs时，r=c·(m·Ts+τ2)=15 006 m。当信噪比为-5 dB时，采用梳状测距导频结构进行OFDM信号测距仿真。表4为不同数量的导频数据，信噪比为-5 dB时的测距精度。

表4 信噪比为-5 dB时，不同数量的导频数据的测距精度

由图6和表4可以看出，测距导频数据占用的子载波越少，传输通信信息的子载波就越多，通信资源占用率越低。当子载波数和导频数都为4 096时，测距导频占用全部的通信子载波，此时，测出的最长有效距离为20 480 m，测距误差可达0.8 m。当测距导频数据占用一半子载波时，测距精度与导频数据占用全部子载波时的精度基本一致，且通信资源占用率降低了一半。

4 结束语

随着移动通信技术的不断更新，大众对高精度位置服务的需求不断增多，通信与导航的融合将是提升位置服务的重要手段，如何降低定位信息占用通信资源的比例也是有待解决的问题。因此，本文提出了基于梳状导频的通导融合测距优化配置方法，在传统的通导融合测距系统中，采用梳状结构的测距导频信号进行测距建模，利用时频域联合估计法来进行测距仿真。仿真结果表明，在不影响通信信息正常传输的情况下，当测距导频数为2 048，信噪比为-5 dB时，测距精度与测距导频未采用梳状结构时的测距精度一致，可达0.9 m，而且极大降低了通信资源占用率。