基于L-M算法和声波融合的TDOA雷电定位改进方法

骆瑶莹， 卞宏志， 刘全桢， 刘保全， 傅正财， 张建勋， 刘亚坤

(1. 上海交通大学 电力传输与功率变换控制教育部重点实验室， 上海 200030；2. 中国石化青岛安全工程研究院 化学品安全控制国家重点实验室， 山东 青岛 266071；3. 国网福建省电力有限公司建设分公司， 福州 350001)

雷电作为一种长间隙强放电现象，产生时伴有强烈的电磁和声波信号[1]，严重影响油罐储运、电力设备、航空航天活动和森林安全等[2-4].雷电定位技术基于雷电产生时的电、磁、声和光等信号特征，通过分析不同信号的传播特性，反演计算得到雷电的位置信息和产生时间[5].雷电定位技术是目前用于研究雷电活动最主要的手段之一[6]，为关键系统的雷电防护和雷电灾害分析提供数据保障[7].

现有雷电定位系统多测量雷电放电时发出的电磁脉冲信号，其测量探头可工作在甚高频、甚低频/低频或极低频等频段，依据多个探头测量得到的雷电电磁脉冲的波峰到达时间和各探头间的时间差，计算确定雷电电磁辐射源的位置和产生时间.由该方法测得的雷电信息主要受探测子站探头的时钟精度、电磁环境和反演定位算法等影响.在雷电定位算法研究中，赵文光等[8]综合利用到达时差定位法(Time Difference of Arrival, TDOA)和方向定位法，通过考虑平差计算剔除粗差的算法，提高了雷电定位的精度.胡志祥等[9]在雷电定位计算中引入粒子群优化算法，得到了更精确的雷电发生位置.郭小红等[10]提出优化果蝇算法，实现了雷电定位结果的快速计算.李涛等[11]利用改进密度聚类算法对雷电位置进行聚类解算，提高了雷电定位的抗误差干扰能力.梁丽等[12]综合密度聚类算法和网格搜索法，降低了电磁探测数据误差等对雷电定位的影响.在实际的TDOA雷电定位系统中，探测子站存在测量误差，因此采用3个及3个以上探测子站的雷电定位系统会出现雷电位置信息难以求解或求解不唯一的问题.如何解决雷电定位计算中的求解问题，且减小探测站与雷电相对位置以及定位网络几何尺寸对计算结果的影响，具有实际应用意义.

安装于我国油罐等系统中的雷电定位系统具备同时采集声波和电磁信息的能力.为充分利用声波和电磁信号, 李皖等[13]利用人工识别雷击电磁脉冲信号法得到了电磁信号与雷声信号的时间差；汤伟等[14]将雷声按点声源处理，利用坐标搜索法进行雷声方向定位.综合已有研究发现，利用雷电放电时的声波和电磁信号同时进行雷电定位可以提高定位精度，但在雷电电磁和声波信号的融合交互方面还需进一步研究.因此，本文提出一种基于Levenberg-Marquardt算法(简称L-M算法)和声波信息融合的TDOA雷电定位改进方法.根据已有探测站点的布站信息，将目标雷电监测区域划分为16个子区域；利用电磁信号的到达时差，在整个监测区域内计算雷电初定位结果，并将其作为依据，动态纳入雷声站点测得的声波信息，避免声波信号在长距离传播时的大幅衰减和畸变.在计算求解雷电发生位置时，利用可融合声波信息分析的L-M迭代算法，得到更精确的最优解.所提方法在TDOA电磁信息中纳入声波信息，可以帮助解决雷电定位计算中的求解问题，提升雷电定位系统的定位精度和抗误差扰动能力.

1 TDOA雷电定位方法

基于TDOA雷电定位系统，利用3个及3个以上探测子站测得的电磁信息，计算雷电电磁脉冲到达各探测子站的时间差，以确定电磁辐射源的位置.TDOA雷电定位系统一般由连接在同一个通信网络上的若干探测站、中心站和用户终端组成[15].其中，探测站主要包括电磁脉冲接收天线、信号处理单元、高精度时钟单元、电源和通信等模块.伴随雷电产生的电磁信号到达接收天线，并由信号处理单元处理获得同步的时间标签后，通信口将电磁脉冲波峰到达探测站的精确时间实时发送到中心站.中心站的雷电位置分析仪根据电磁脉冲到达各探头的时间差来确定雷电电磁辐射源的位置，并由中心站将定位结果输出到各用户工作站.在保证系统运行可靠性的基础上，多个定位系统联网可以实现数据共享，满足雷电定位系统的扩展需求[16].

在雷电电磁信号测量中，雷电辐射源产生的电磁波到达探测站#1和探测站#2的时间差为Δt12，结合两个探测站的地理位置信息，可以确定一条双曲线，其计算式为

(1)

式中：(x1,y1)和(x2,y2)分别为TDOA探测子站T1和T2的位置坐标；c为电磁波传播速度，且c=3×108m/s.根据双曲线交汇原理，电磁波辐射源可以由交汇点位置坐标确定.在3个及3个以上探测站的情况中，不同双曲线相互交汇并产生公共交点，据此可以确定雷电发生位置.

在TDOA雷电定位的实际计算中，双曲线发散的几何形状特性导致整个雷电监测区域的定位精度不均匀[17].采用3站TDOA定位可能会出现两条双曲线交于两点的情况，导致雷电定位系统作出伪雷击位置判断[18].对于3站以上的TDOA定位系统，电磁波探测站在测量时存在误差，因此利用探测站之间的时间差信息得到的多条双曲线不易交于一点，从而影响基于到达时差信息的雷电定位方程组求解.对此，通常利用优化算法来减小测量误差的影响并解决方程组的求解问题[8-12].

2 基于L-M算法和声波信息融合的TDOA雷电定位改进方法

2.1 L-M迭代算法

L-M算法是牛顿法的一种改进.在计算时，其能够避免牛顿法由于Hessian矩阵奇异而导致算法无法继续迭代的情况[19]，常用于非线性最小二乘问题的最优化实现，能够有效解决时差信息冗余时雷电位置最优解的求解问题.

L-M算法用于雷电定位计算时的流程如图1所示.其中，L0为雷电初定位结果，即L-M算法的迭代初值.在求解由多个探测子站的声波信息得到的非线性方程组f(x)=0时，可转换为最小值寻找问题：

图1 利用L-M迭代算法进行雷电定位计算的流程图Fig.1 Flow chart of lightning location calculation using L-M iterative algorithm

(2)

式中：x为需求解的雷电定位结果.高斯-牛顿法将迭代步长设定为

(3)

式中：I为单位矩阵；μ>0保证系数矩阵正定，从而保证迭代的下降方向，克服了因Hk不可逆而导致的迭代无法继续问题.为保证算法在接近最优解时能够快速收敛[20]，当μ较大时，

当μ较小时，

hlm≈hgn

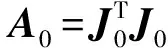
其中：τ为限定μ0在适当数值的系数.μ的数值更新由系数ϑ决定：

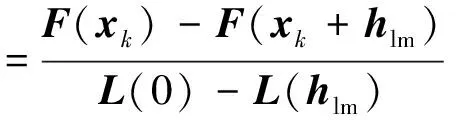
(4)

式中：F(xk)-F(xk+hlm)表示目标函数在步长hlm下的实际变化；L(0)-L(hlm)表示目标函数的预估变化值，其计算式为

(5)

(6)

‖xnew-x‖<ε2(‖x‖+ε2)

(7)

k>kmax

(8)

式中：ε1和ε2为迭代终止的条件参数；kmax为最大迭代步数，合适的kmax值可以防止迭代无限循环引起的算法崩溃.ε1、ε2和kmax主要根据L-M算法的具体应用情况进行选取，对算法最终收敛结果影响不大.在本算法中，设ε1=ε2=10-12，kmax=200.在计算过程中，3个参数的取值满足上述条件之一即终止算法，输出雷电定位计算结果.当探测站测得的信号存在误差或信息冗余时，会导致雷电定位计算无法得到非线性方程的唯一解，而L-M迭代算法可以为寻找雷电位置最优解提供可靠的算法支持.

2.2 融合声波信息的TDOA定位

TDOA雷电定位系统对测试精度要求较高，其中，探测站布局方式会引起时间误差[21]，雷电电磁波峰值点因传播路径和距离的不同而发生漂移或畸变，导致时间测量误差[22]，使得TDOA的定位误差幅值达到几百米或几千米.此外，整个雷电监测目标区域的TDOA雷电定位精度不均匀，存在局部定位误差较大的区域块.雷电发生时会发出强烈的电磁信号和声波信号.声波信号的传播特性与信号频率有关，在相同距离和环境背景下，信号频率越低则声波传播性能越优异[23].随着传播距离的增大，低于 100 Hz 的声波信号幅度衰减速度较慢，可以作为有效的雷声信息进行雷电定位研究.因此，可以考虑在进行雷电定位时纳入雷声声波信息来减小局部区域块的定位误差，从而提升整个雷电监测目标区域的雷电定位效果.

在TDOA雷电定位系统融合声波信息时，利用波形延时压缩处理技术可以有效发送声波信号，减小声波信号传递带来的影响[14].为提高所纳入雷声声波信息的准确性，综合根据已有TDOA探测子站和雷声探测站的位置信息，将整个雷电监测区域进行子区域划分处理，如图2所示.其中，T3和T4为TDOA探测子站，N1～N4为4个雷声探测站.共划分为16个雷电监测子区域.其中，子区域#1、#4、#13和#16为近时差站子区域，子区域#6、#7、#10 和#11为近雷声站子区域，子区域#2、#3、#5、#8、#9、#12、#14和#15为时差-雷声站点近似等距子区域.以TDOA探测子站与子站之间的连线(蓝色线)为边界，将线内区域定义为探测网内区域，线外区域即监测边缘区域定义为探测网外区域.在处理雷声信号时，将极短时间内连续的多点声源近似处理为单个定位计算所需要的雷声点声源信号[13].在接收雷电放电时，声波信号雷声站中的声波麦克风(M0～M4)阵列布置方式为十字阵列排布，如图3所示.

图2 TDOA探测子站和雷声探测站布局Fig.2 Site location of TDOA lightning location sensors and acoustic sensors

图3 十字麦克风阵列示意图Fig.3 A diagram of crossed microphone array

当雷电发生在目标监测区域内时，4个TDOA探测子站会采集到一套相应的雷电电磁信息，依据测得的雷电电磁时间信息，可列出由3个互相独立方程组成的方程组：

(9)

式中：(x3,y3)和(x4,y4)分别为T3和T4的位置坐标.

利用式(9)计算得到雷电初定位结果(单一点)，记为L0=(x0,y0).根据初定位坐标判断雷电发生位置所在的子区域.同时，利用子区域最小距离判定并选取合适的麦克风阵列，进行麦克风阵列所探雷声信息的融合和求解.根据测得的雷声声波信息、麦克风阵列相对位置和声波传播特性，得到

(10)

式中：(xi,yi)和(xj,yj)分别为麦克风Mi和Mj的坐标；Δtij为雷声到达时差；v为声波传播速度.

由此可知，对于包含多个麦克风的测量阵列系统，如由5个麦克风组成的测量阵列系统可以得到10个约束方程，即使在少数麦克风传感器工作失效的特殊情况下，其仍能够获得足够的雷声信息.纳入雷声声波信息后，方程组中的方程数目大于未知数数目，可以采用L-M算法进行迭代计算，求出雷电位置的最优解.

基于L-M算法和声波信息融合的TDOA雷电定位算法的整体流程如图4所示.利用TDOA探测子站测得的电磁信号及其时间信息，判定雷电初定位结果.根据L0所属子区域k′的判断结果，调取距离子区域k′最近的雷声站n′测得的声波信息，并将其纳入非线性方程组，利用L-M迭代算法计算更精确的雷电位置.

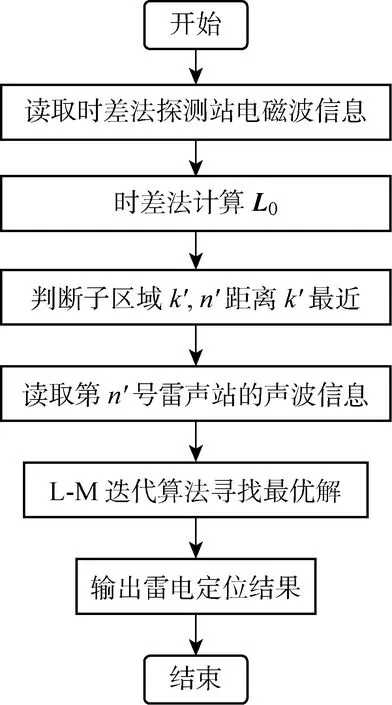
图4 基于L-M算法和声波信息融合的TDOA雷电定位算法流程Fig.4 Flow chart of TDOA lightning location approach considering acoustic information and L-M algorithm

2.3 算法验证

在MATLAB中完成所提方法的算法编写，并利用蒙特卡罗法[24]对雷电定位法进行精度评估.以边长为40 km的正方形雷电监测目标区域为例，据图2中x轴和y轴建立坐标系4个时差法探测子站 T1～T4探头位置的坐标分别为(15, 15)(-15, 15)(-15,-15)和(15,-15)；4个雷声站N1～N4的中心麦克风位置的坐标分别为(8, 8)(-8, 8)(-8,-8)和(8,-8)；图3中M1～M4与M0的距离均为20 m.

依据蒙特卡罗法，以2 km为空间步长将 40 km×40 km的雷电监测区域进行网格划分，将区域内的441(21×21)个格点分别作为雷电发生位置进行雷电定位精度评估，具体步骤如下：

步骤1计算在某格点处产生的雷电电磁波和声波信号到达每个探头的准确时间.

步骤3分别利用TDOA定位的传统法和所提改进法进行雷电位置计算，得到相应的雷电定位结果.

步骤4评估雷电定位结果的误差，即雷电发生的实际位置与定位计算结果之间的绝对差值.

步骤5重复步骤2至步骤4共100次，得到以该格点作为雷电发生位置的100次定位结果和定位误差，并将100次定位误差的均值作为该格点的最终定位误差值.

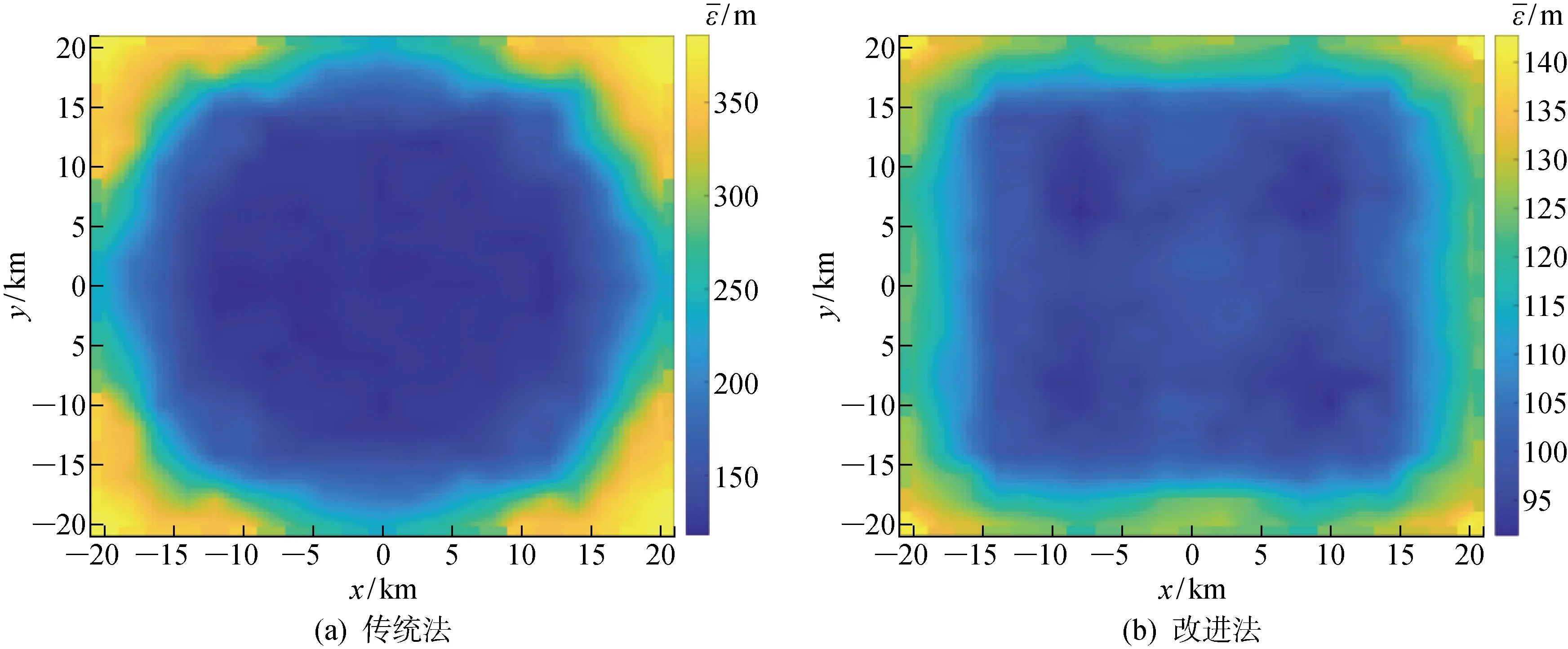
图5 雷电定位误差分布Fig.5 Error distribution of lightning location

表1 不同子区域的雷电定位误差均值

TDOA雷电定位传统法和改进法在不同子区域内的误差均值分布如图6所示.结合图5可知，改进法利用雷电监测区域测得的电磁时差信息开展雷电活动的初步定位，根据初步定位结果动态选取距离最近的雷声站信息，同时融合电磁和声波信息进行雷电活动精准定位，以改善整个监测区域的雷电定位效果.传统法在探测网内的定位误差为120～200 m，在探测网外的定位误差接近300 m，在整个目标监测区域内的定位误差均值为203.2 m，均方差为82.8；改进改法在探测网内的定位误差为90～110 m，在整个目标监测区域内的定位误差均值为108.4 m，定位精度提高了46.6%，均方差为27.3.此外，利用传统法定位时，位于监测区域边缘的雷电定位误差明显增大；而利用改进法进行定位时，位于监测区域边缘的雷电定位误差得到改善，雷电定位精度比传统法提高了51.2%.

图6 不同子区域的雷电定位误差均值分布Fig.6 Average lightning location error distribution in different sub-regions

3 结语

本文提出一种基于L-M算法和声波信息融合的TDOA雷电定位改进方法，根据TDOA探测子站和雷声探测站的位置信息，将目标监测区域划分为16个子区域.利用电磁时差信息完成雷电的初步定位计算，并根据初定位结果动态纳入雷声站探测得到的声波信息.同时，利用L-M算法对融合的声波信息进行计算，求解雷电位置最优值.采用蒙特卡罗法分别对TDOA雷电定位传统法和所提改进法进行精度评估，发现传统TDOA雷电定位系统的定位误差在整个监测区域分布不均，在目标区域边缘的雷电定位精度下降明显，误差均值为203.2 m，所算结果均方差为82.8；所提方法经过声波信息融合和L-M算法改进后，能够有效降低区域误差不均匀的程度并提高雷电监测区域边缘的定位精度，误差均值为108.4 m，目标监测区域整体定位精度提高了46.6%，所算结果均方差为27.3.所提方法能够对已有雷电定位系统的改进和声波信息的融合利用提供参考.