Air combat decision-making of multiple UCAVs based on constraint strategy games
2022-03-29ShouyiLiMouChenYuhuiWangQingxianWu
Shou-yi Li,Mou Chen,Yu-hui Wang,Qing-xian Wu
College of Automation Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing,211100,China
Keywords:Game theory Time-sensitive information Constraint strategy games Polytope strategy games Multiple UCAVs Air combat decision-making
ABSTRACT
1.Introduction
The developing science technology and arti ficial intelligence make it possible to achieve autonomous air combat decisionmaking for unmanned combat air vehicle(UCAV)in military warfare[1,2].Due to the limitations of detection capabilities and weapon attacks,it is dif ficult for a single UCAV to complete a complex air combat mission.Therefore,multiple UCAVs can cooperate in combat,perceive the battle field situation through the shared information of the communication equipment,and realize coordinated task allocation,search,reconnaissance and attack,which can effectively improve the survivability of UCAVs and overall combat effectiveness[3,4].Therefore,it is particularly important to realize the autonomous air combat decision-making during the cooperative operation of UCAVs.The development of this technology will open up a new situation in future wars[5-7].
In the existing literatures,the air combat decision-making of multiple UCAVs is usually considered as a unilateral optimization problem,which only considers the best strategies of one UCAV group,but does not predict and analyze the opponent’s strategies.It usually adopts the following intelligent methods to obtain the decision result.In Ref.[8],a decision method was proposed based on the expert system,but this method relies on expert experience,and the selected strategy may not be the best result.A framework for multiple UAVs task assignment based on hierarchical task assignment method was constructed in Ref.[9],and the original problem was broken down into three levels of sub-problems:target clustering,cluster allocation and target assignment,which can reduce the computational complexity of the task assignment problem.An evolutionary algorithm in machine learning was considered to train large-scale UCAVs in Ref.[10],as the training number increases,the UCAVs show increasing intelligence.There is no doubt that these results have made a lot of valuable progress,but the impact of enemy strategies on the optimal solution has not been considered.Since the UCAVs air combat decision-making system is a system that interacts with two or more participants,it is unreasonable to consider only the actions of one party in the air combat decisionmaking of multiple UCAVs.
Game theory is one of the effective tools to analyze the competitive relationship among multiple participants,and it has played a signi ficant role in economics,management sciences,operational research,engineering,social sciences,biology,etc[11].Game theory also has many applications in some special issues in the field of air combat decision-making,such as the use of differential games to study pursuit-evasion,missile guidance,etc[12],but the study of game theory in multiple UCAVs air combat decision-making has just started.Game theory was first used to study the confrontation between two helicopters in Ref.[13].Although the game model was relatively simple,it inspired the future research.An attrition-type discrete-time dynamic model was formulated for two opposing forces in Ref.[14],in which a onestep look ahead moving horizon optimization was considered.However,this is only a static game model and does not always have a pure strategy Nash equilibrium solution.A moving horizon solution approach was proposed in Ref.[15]to reduce the computing dif ficulty of complex air combat systems.Many researchers also applied other game methods to study decision-making problems,such as stochastic games[16],dynamic games[4],differential games[17],fuzzy games[18],etc,and achieved many valuable results.However,these methods rarely take into account the impact of time-sensitive information on decision-making results in the complex air combat environment.
There is often a lot of time-sensitive information in a complex air combat environment[19],such as detecting that a certain target is the control center of the enemy UCAVs,or some enemy UCAVs are predicted to attack our ground base,or some of our UCAVs have equipment failure,or certain targets entering dangerous airspace,etc.The time-sensitive information can greatly affect air combat decisions,so it has a greater priority than air combat situation information and need to be considered first[20,21].Decisions for time-sensitive information are given by the airborne expert system,which speci fies the probability range for executing certain strategies under speci fic time-sensitive information.The decisionmaking rules of the airborne expert system are based on the experience of military experts,which are quantitative and vague.Therefore,the decisions for time-sensitive information are manifested in the estimation of the probability of executing speci fic strategies.For example,if a target is the control center of the fleet,the target should be attacked with a greater probability;if a certain UCAV has equipment failure,the UCAV should perform the attack mission with a small probability,etc.Decisions for time-sensitive information form linear constraints of mixed strategies in the game,and under these linear constraints,air combat decisionmaking are made based on the air combat situation information.This kind of game model with linear constraints is called the constraint strategy game.
Traditionally,the Nash equilibria of mixed strategy games can be calculated by solving a pair of dual linear programming problems[22]due to that each mixed strategy of a player is the convex combination of pure strategies,and it can turn the in finite inequality constraints of Nash equilibrium into finite inequality constraints.We find that in constraint strategy games,the strategy space of each player is a polytope,and the strategy of each player is the convex combination of the extreme points of its strategy set.Therefore,the constraint strategy game can be solved in a similar way to the mixed strategy game.
The main contributions of this paper are given as follows:
(i)Considering the time-sensitive information in the complex air combat environment,a constraint strategy game model is presented.
(ii)The polytope strategy games are studied and some general results are given,which are speci fied as an algorithm(CSG-LL algorithm)to solve the constraint strategy game.Thereby,the air combat decision-making results of multiple UCAVs are obtained.
The structure of this paper is as follows.In Section 2,an air combat situation assessment approach and a constraint strategy game are introduced.In Section 3,the polytope strategy game is discussed and some results on its solutions are given,which are speci fied as CSG-LL algorithm to solve the constraint strategy game.Thereby,the air combat decision-making results are obtained.In Section 4,an example is given to illustrate the effectiveness of the proposed approach.
The notations in this paper are shown in Table 1.
2.Problem formulation and preliminaries
Assume that there are two confrontational UCAV groups in air combat,the Red UCAV group R and the Blue UCAV group B,and UCAV group R consists of m UCAVs,denoted as R,R,…,R,UCAV group B consists of n UCAVs,denoted as B,B,…,B.The air combat decision-making process of R and B includes modeling the air combat situation assessment and solving the proposed constraint strategy game,which is shown in Fig.1[23].
2.1.Review of air combat situation assessment
The air combat situation of R(i=1,2,…,m)and B(j=1,2,…,n)is given in Fig.2[24],where the symbols are de fined in Table 1.
For different UCAVs with different positions,speeds,weapons and equipment,they have different decision results.Firstly,to describe these differences,the air combat situation assessment is conducted,which is the foundation of the following air combat decision-making.
Through the airborne sensors and ground station,the following parameters of each UCAV can be obtained:the position,the speed,the maximum missile attack distance,the maximum radar detection distance and the number of missiles carried,as shown in Table 1.

Table 1 Notation table.
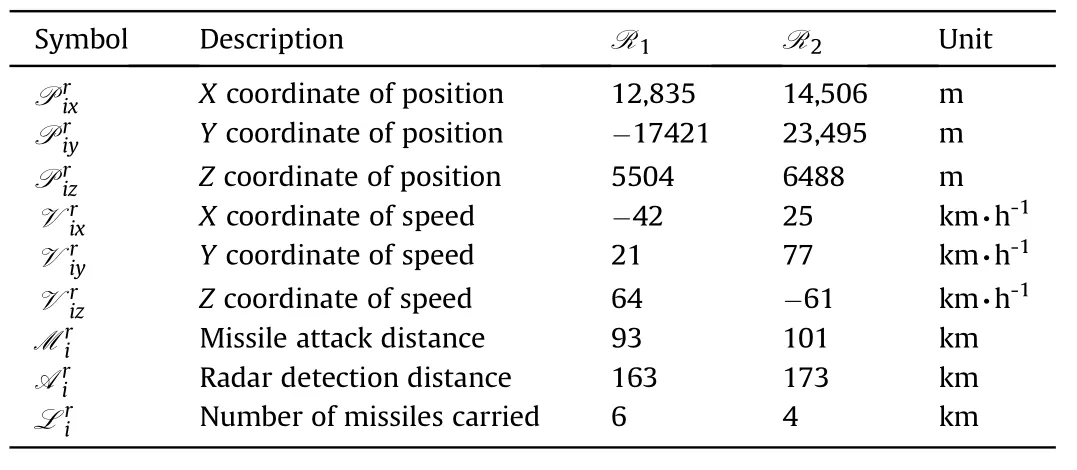
Table 2 Parameters of R.
The situation assessment includes angle priority,velocity priority,distance priority,high priority and performance priority[24,25].The priority computation equations for R to B are as follows:




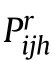
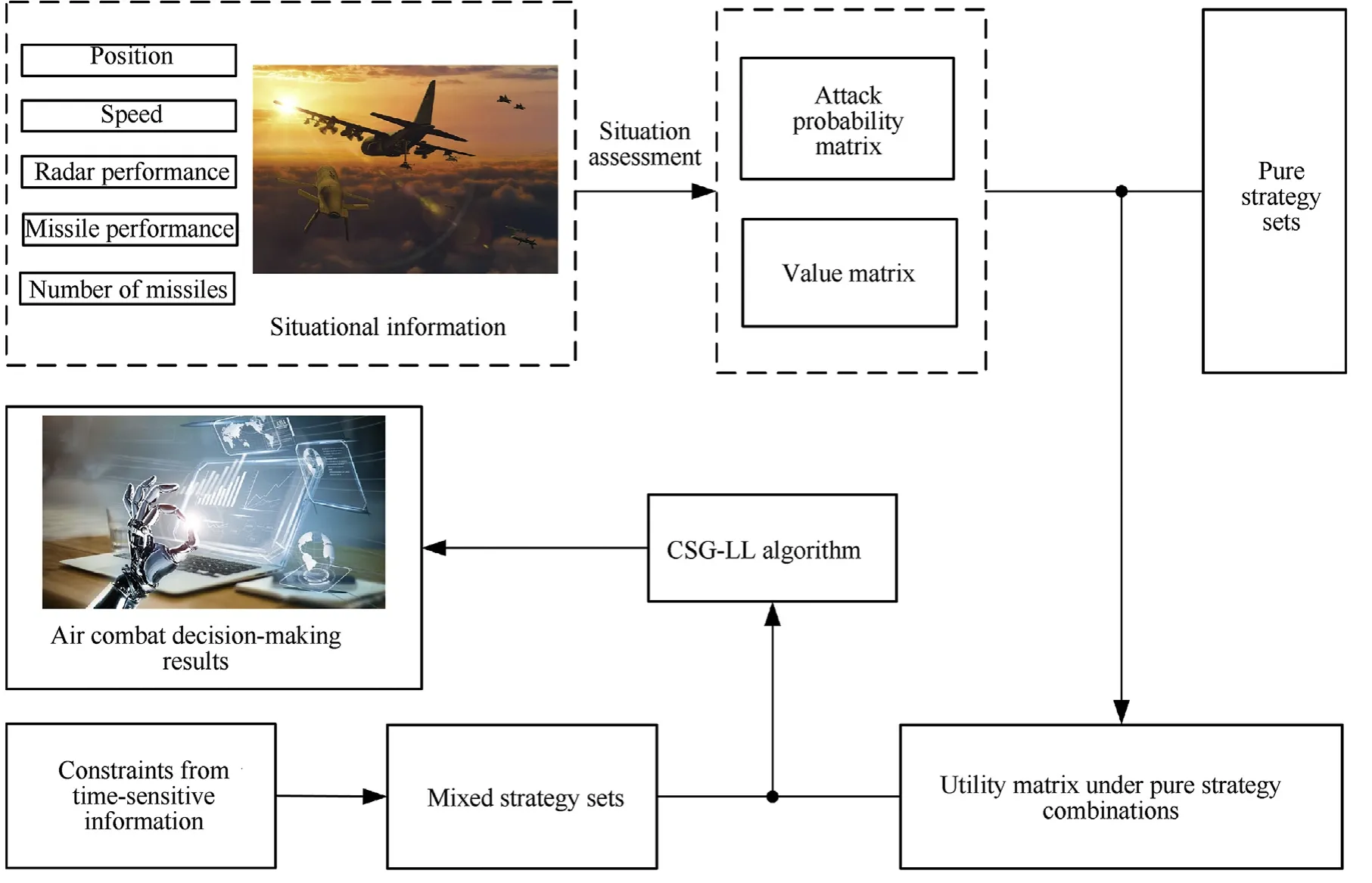
Fig.1.Air combat decision-making process of R and B.
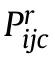
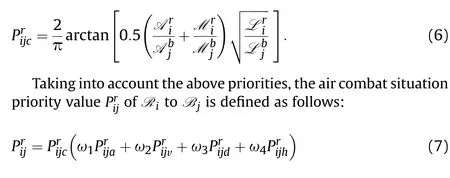
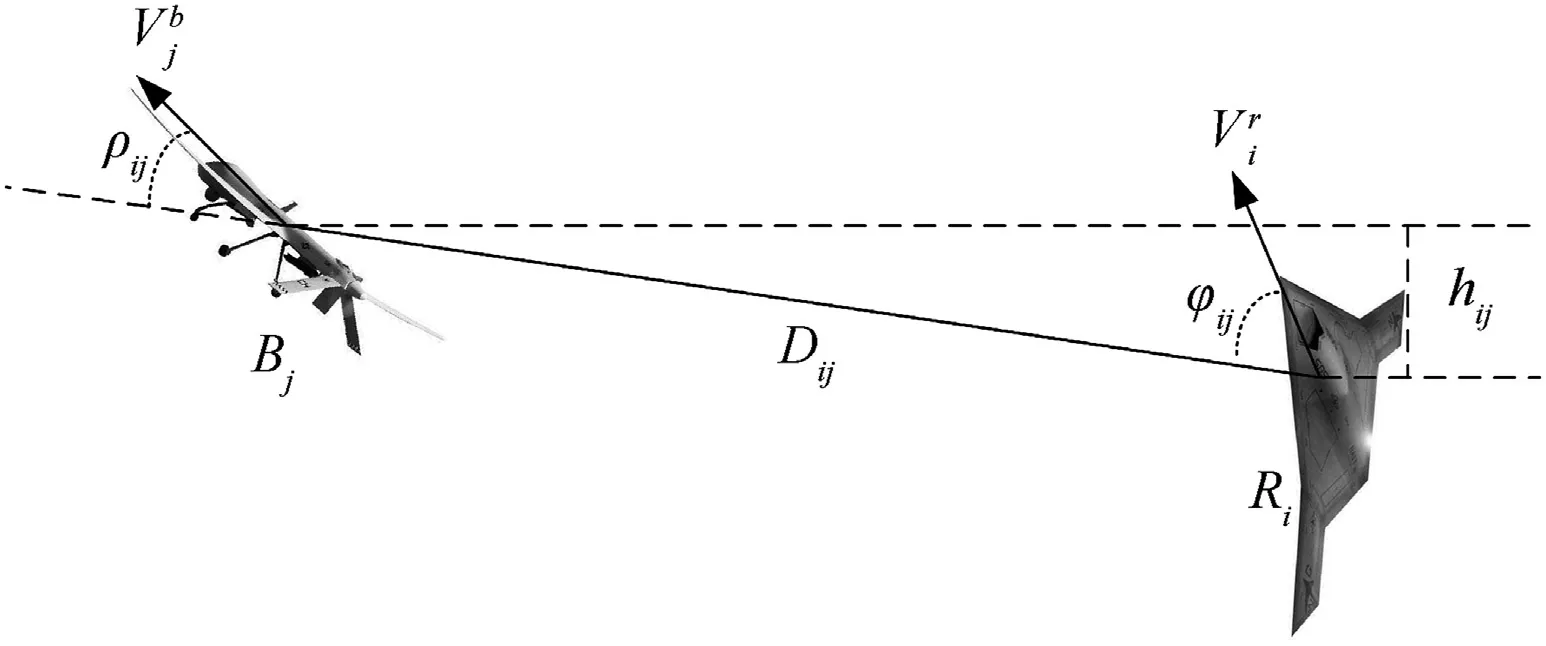
Fig.2.Air combat situation of R and B.
whereω,ω,ω,ωare the weighting coef ficients,determined by experts.
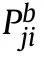
2.2.The constraint strategy game of R and B
In this part,we establish a constraint strategy game model for the air combat decision-making process of R and B.
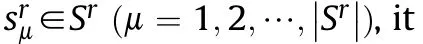


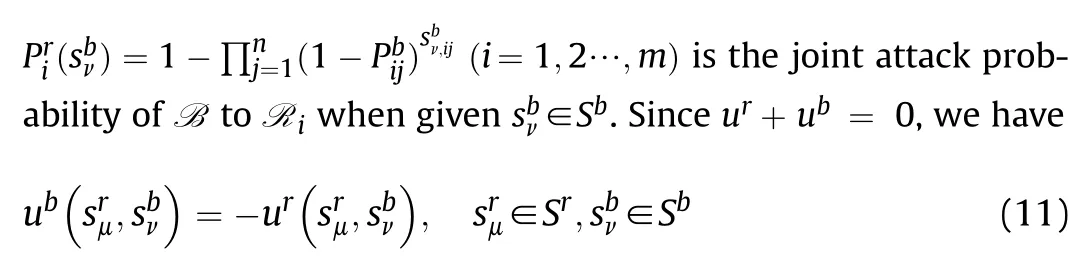
Nash equilibrium is a widely recognized solution concept in game theory.A pure strategy combination(s,s)is the Nash equilibrium of G=〈S,S,u,u〉,if it satis fies the following inequalities[29]:

where U(σ,σ)is the expected utility under the mixed strategies combination(σ,σ),and U(σ,σ)=-U(σ,σ)is the utility function of B.
As we discussed in Section 1,there is a lot of time-sensitive information in air combat,and the time-sensitive information is more important than the air combat situation information,so they need to be prioritized in air combat decision-making.Firstly,the expert system gives rough decision based on time-sensitive information.In the expert system,the inference engine matches the time-sensitive information with the rules in the knowledge base.Under such case,the execution probabilities of some pure strategies are given,which are the linear constraints of the mixed strategies.Then,on the basis of linear constraints,the numerical computing system gives precise decision based on situation information.The matrix game of R and B with linear constraints forms the constraint strategy game,then based on situation information,the Nash equilibrium strategy is obtained by solving the constraint strategy game.The roles of time-sensitive information and air combat situation information in air combat decision-making are shown in Fig.3.
In addition,as long as they are linear constraints,the final strategy set constitutes a polytope,which can be solved by our method.In this paper,we might as well consider a simple scenario:a certain UCAV is the control center of its fleet and need to be shot down with lager probabilities.Therefore,the linear constraints can be added to the execution probabilities of certain strategies.
A perturbation vector of G=〈S,S,u,u〉is applied to characterize these constraints[29].

where Uis de fined in equation(14).

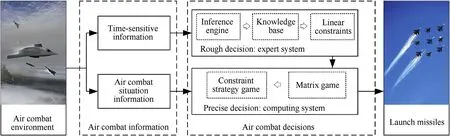
Fig.3.Roles of time-sensitive information and air combat situation information.
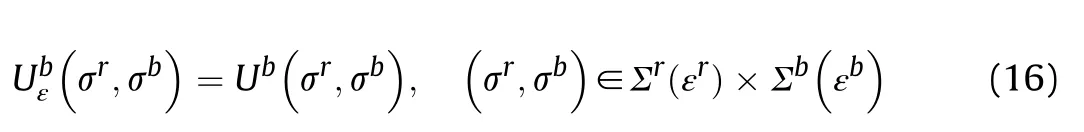
The de finition of the Nash equilibrium solution of G(ε)is given below,which is similar to that of G.
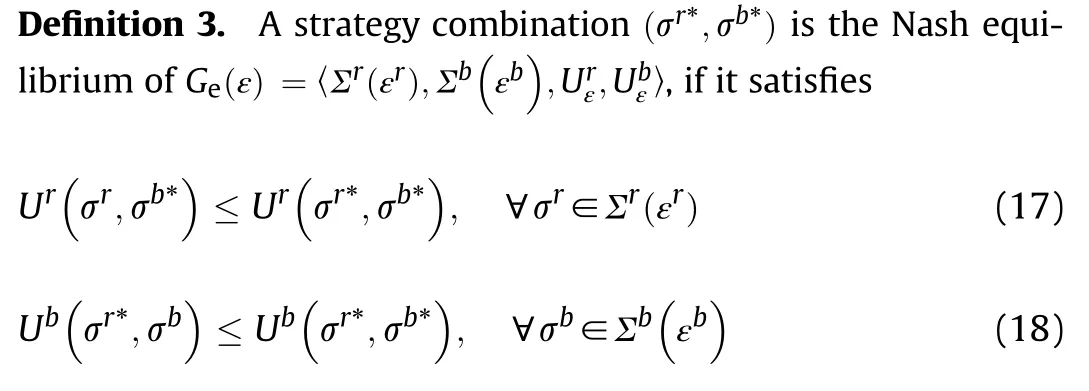
2.3.Geometric structures of constraint strategy set
We know that a polytope inℝis a bounded set which is the intersection of a finite number of half-spaces;A simplex inℝis a special polytope whose extreme points are unit vectors e,e,…,e.It is obvious thatΣandΣare both simplexes.In the following we will show thatΣ(ε)andΣ(ε)are the polytopes inℝ|S|andℝ|S|,respectively.

In other words,Σ(ε)andΣ(ε)are the convex hulls of their extreme points,respectively.A method is given to calculate the extreme points ofΣ(ε)andΣ(ε)in Appendix A.Algorithms for calculating the extreme points of an arbitrary polytope can be found in Ref.[30].
So far,we have conducted the air combat situation assessment and established the constraint strategy game model for the air combat decision-making problem with constraints from human experience,following we will give an algorithm to calculate the Nash equilibrium solution of the proposed model,thereby the air combat decision-making results of R and B are given.
3.Main result
In this section,the polytope strategy game is studied and some general results are given on the basis of[29],and these results are speci fied as an algorithm to solve the constraint strategy game G(ε)based on the algorithm for solving the mixed strategy game in Ref.[22].
3.1.Polytope strategy games

Proof.As we stated above,every polytope strategy game of R and B has a Nash equilibrium.By using Lemma 2,a polytope strategy game has a value if and only if it has at least one Nash equilibrium.Thus,we proved that every polytope strategy game has a value.
The above theorem guarantees the existence of the value of G,and the value of Gcan be calculated by the following theorem.

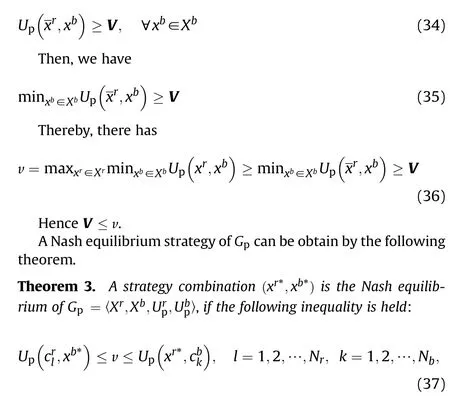
where v is the value of G.
Proof.Assume that v is the value of G,then v satis fies(37).Since Xand Xare both polytopes,for each x∈X,xcan be written as a convex combination of all the extreme points of X.Similarly,for each x∈X,xcan be written as a convex combination of all the extreme points of X:

Remark 2.Theorem 3 simpli fies the de finition of the Nash equilibrium of G.To judge whether a strategy combination(x,x)is a Nash equilibrium of G,we only need to check whether it satis fies the finite number of inequalities in(37).The theorem makes it unnecessary to check in finite inequalities in the de finition of Nash equilibrium,which makes it possible to solve or verify the Nash equilibrium of G.
We know that there must be a Nash equilibrium solution in a polytope strategy game,but the uniqueness of the Nash equilibrium of a polytope strategy game cannot be guaranteed.In fact,any solutions of(45)and(46)constitute a Nash equilibrium of G.Fortunately,the Nash equilibria of Ghas the following good properties,which are the generalization of the properties of matrix games[31].
Theorem 4. For any two Nash equilibria(x,x)and(x,x)of G,we have

Proof.See Appendix D.
Because Ghas the above properties,even if R and B choose strategies in different Nash equilibria,they will also constitute a Nash equilibrium of G,and different Nash equilibria have the same utility value for R and B.
Through Theorem 3,a strategy combination(x,x)is a Nash equilibrium of Gif it satis fies

3.2.An algorithm for solving constraint strategy games

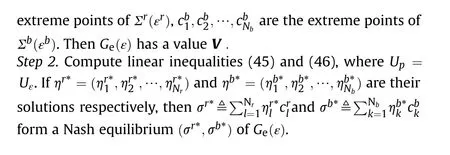
In our algorithm,we implicitly assume that both parties have established the same utility function.But as we have seen,the utility function involves many parameters,and it is a very limited assumption to establish the same utility functions for both sides without any communication.
In fact,as long as the utility function established by oneself is accurate,its decision results obtained by the proposed algorithm will be effective,no matter whether the other party establishes the same utility function or not.The following proof is given.Suppose that Uand Uare the utility functions of R established by R and B respectively,(σ,σ)is the Nash equilibrium calculated by Uand(σ,σ)is the Nash equilibrium calculated by U.We assume that Uis the real utility function.According to the de finition of Nash equilibrium,for allσ∈Σ(ε),we have U(σ,σ)≥U(σ,σ),thereby,U(σ,σ)≥U(σ,σ).In other word,even though R and B have established different utility functions and both adopt the Nash equilibrium strategy calculated by themselves,as long as the utility function of R is accurate,R can ensure that the utility obtained is not lower than U(σ,σ).The above conclusion is guaranteed by U+U=0,for general sum games,utility cannot be guaranteed without establishing the same utility function.
We implicitly assume that both parties have established the same utility,so the utility function is common knowledge,in other words,the constraint strategy game we proposed is a complete information game.When one party does not know what utility function the other party has established,in other word,the utility function is not common knowledge,then the game is an incomplete information game.
As we have seen,our decisions are made under the current air combat situation.However,air combat is a dynamic process.If the air combat situation changes,the decisions must be adjusted accordingly.Therefore,in the execution of the attack decision process,a module is introduced to detect whether the air combat situation has changed.If the air combat situation changes,the algorithm will run again based on the new air combat situation,and new assignments will be made;if the air combat situation does not change,the attack will be executed according to the decision result until the end of the air combat(win or lose).The air combat decision-making of multiple UCAVs based on CSG-LL algorithm is shown in Fig.4.
In summary,we have studied the polytope strategy games(a generalized matrix game)and applied the research results to the constraint strategy game(matrix game with linear constraints).An algorithm for solving the constraint strategy game has been given,at the same time,intelligent decisions for multiple UCAVs in air combat with air combat situation information and time-sensitive information are obtained.
4.Numerical example
In this section,an example is given to verify the effectiveness of the CSG-LL algorithm.
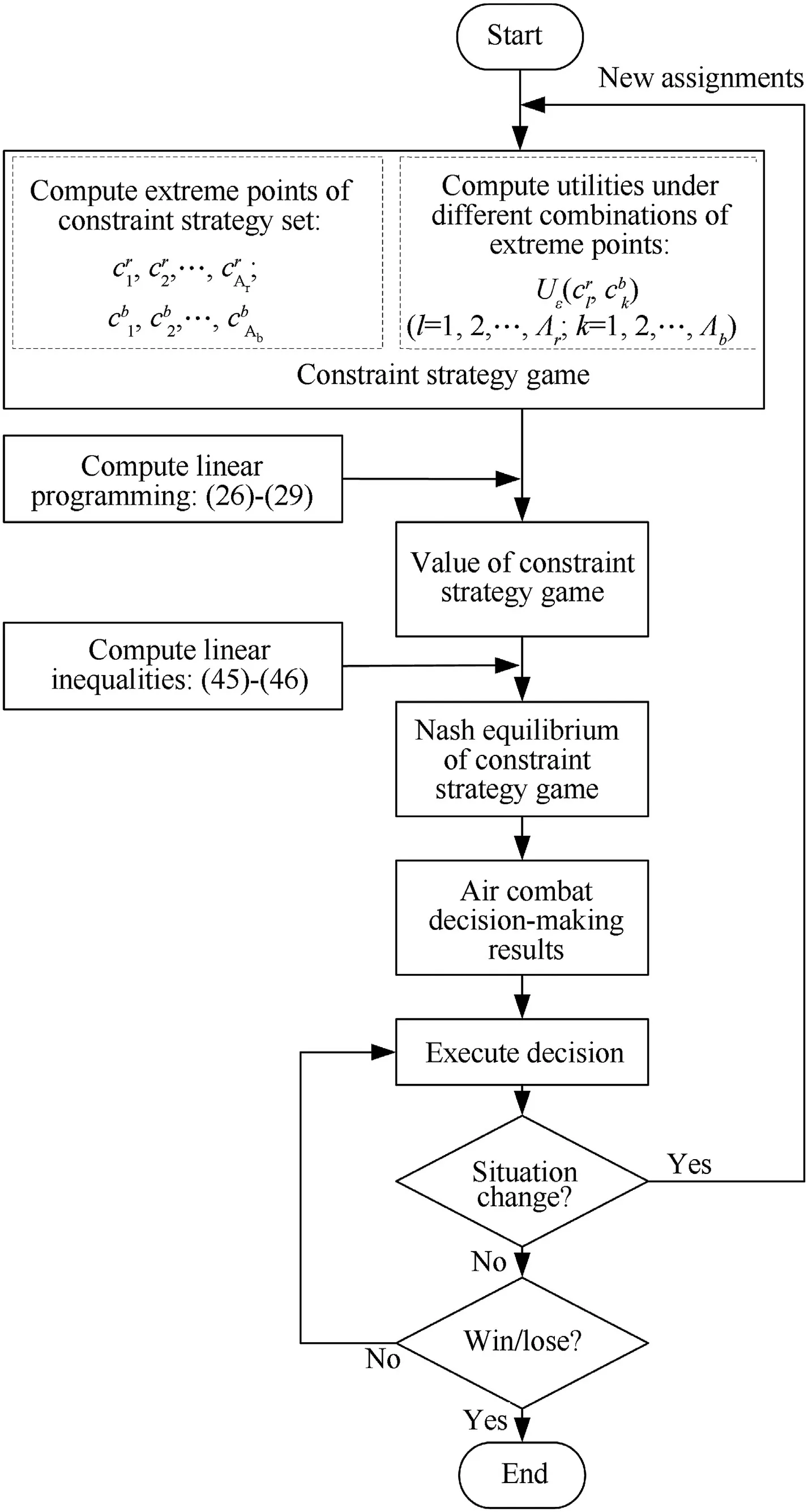
Fig.4.Air combat decision-making of multiple UCAVs based on CSG-LL algorithm.
Suppose that UCAV group R has 2 UCAVs:Rand R,and UCAV group B has 4 UCAVs:B,B,Band B.Based on the related literatures and our previous work accumulation,their parameter values are given in Table 2 and Table 3,respectively.
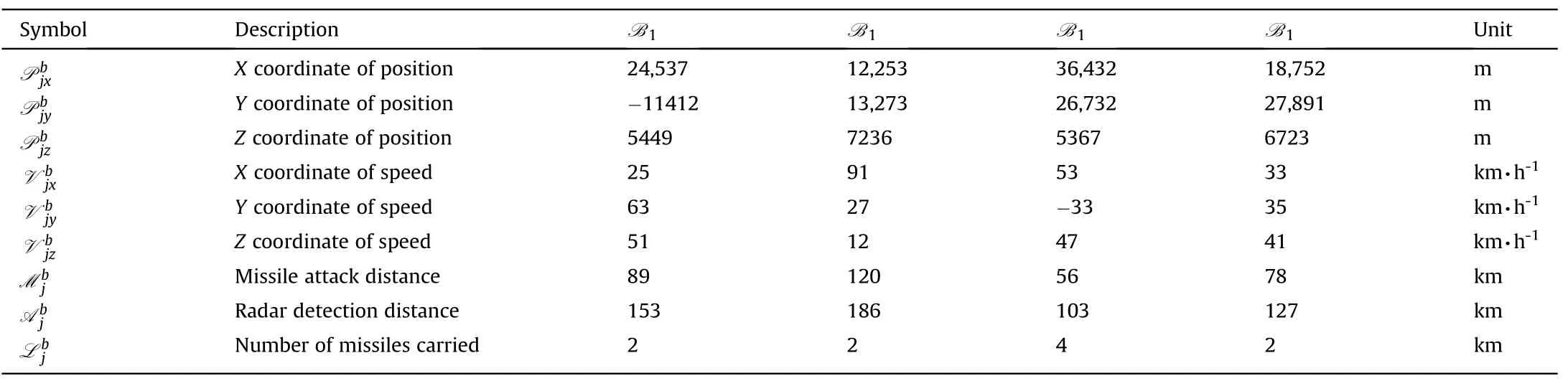
Table 3 Parameters of B.
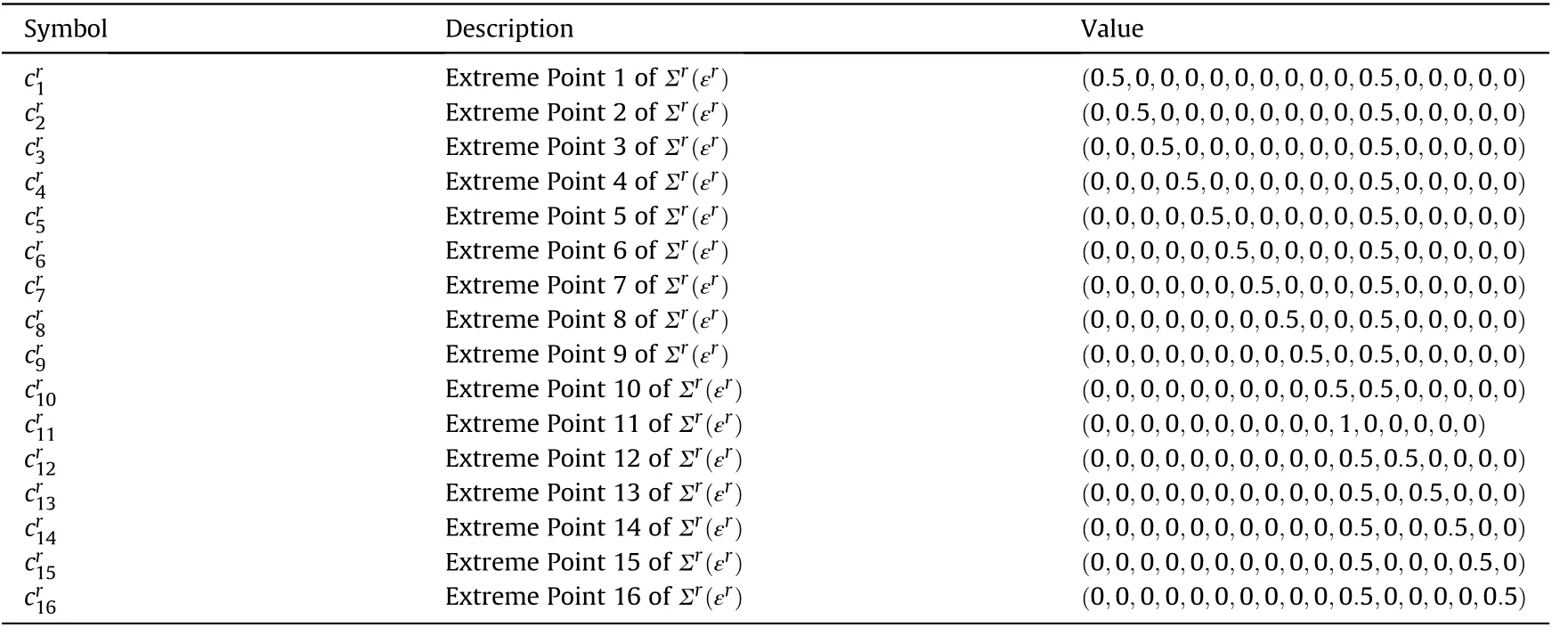
Table 4 Extreme points ofΣr(εr).
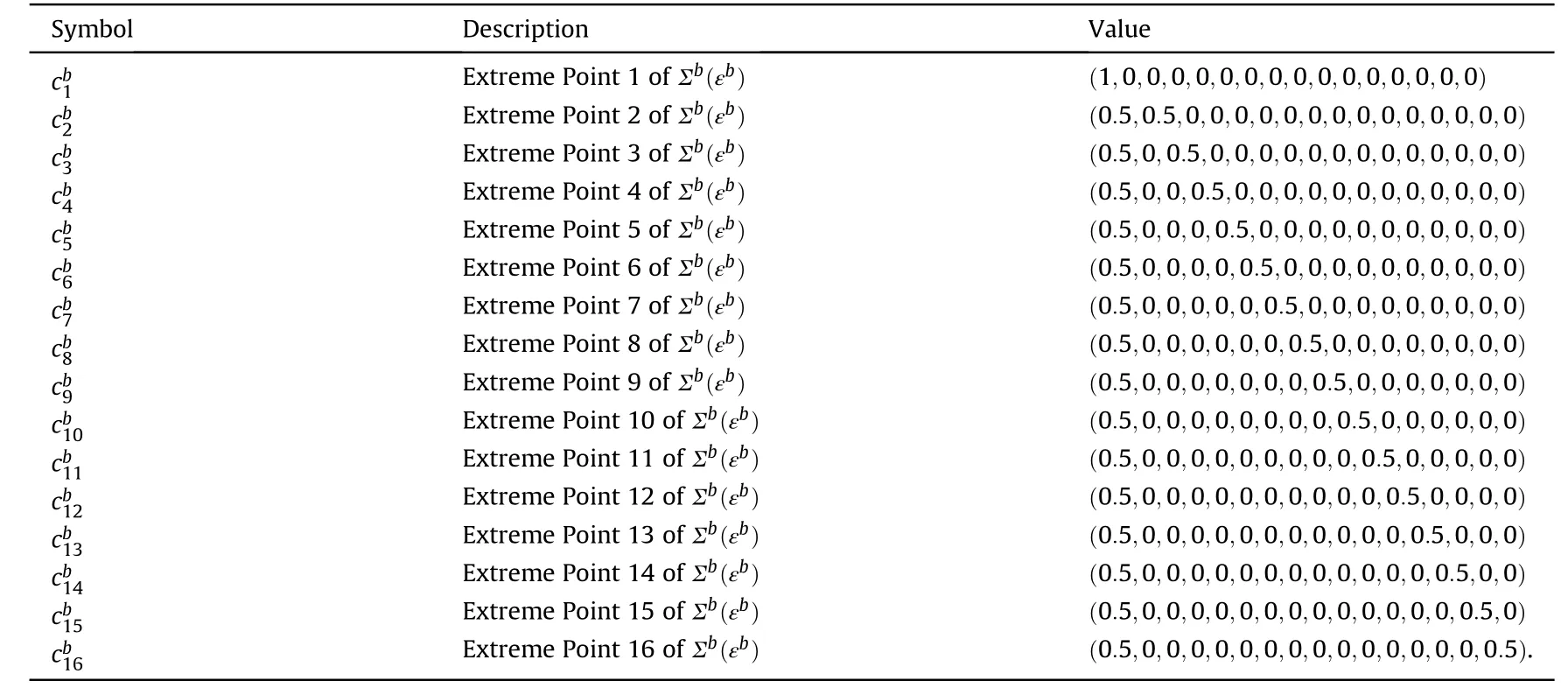
Table 5 Extreme points ofΣb(εb).
In Eq.(7),takeω=0.4,ω=0.3,ω=0.2,ω=0.1 according to expert experience,the attack probability matrices of R and B are obtained:
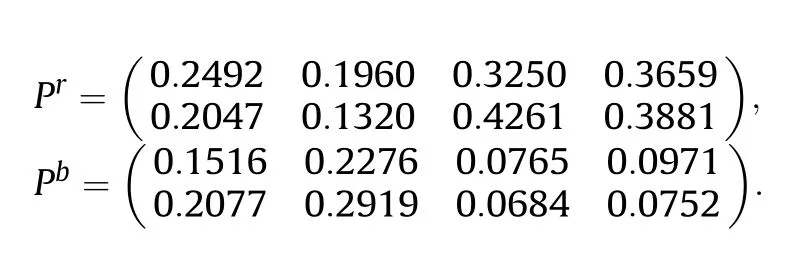
Based on the attack probability matrix Pand P,the value matrices of R and B are calculated as:
Then we obtain constraint strategy setsΣ(ε)andΣ(ε),which are all polytopes inℝ.



The value of the game can be calculated as-0.4726 by(47)-(50),and the Nash equilibrium strategy(σ,σ)is obtained according to (51) and (52), where σ= (0,0,0,0,0.5,0,0,0,0,0,0.5,0,0,0,0,0),σ=(0.5,0,0,0,0,0,0,0,0,0,0,0,0.5,0,0,0),which gives the probabilities of R and B choosing their respective pure strategies.According to the pure strategies given in Appendix E,the Nash equilibrium strategy can be written as the attack probabilities of each UCAV to different targets.The attack methods of R and B according to the Nash equilibrium strategy is shown in Fig.6.

Fig.5.The attack methods of R and B according to the Nash equilibrium strategy.
5.Conclusions
In view of the fact that there is time-sensitive information in air combat and need to be prioritized in complex air combat environment,a constraint strategy game model has been proposed,then the CSG-LL algorithm has been given to solve constraint strategy game.Numerical example has shown that the Nash equilibrium obtained by CSG-LL algorithm can meet the requirements of the given constraints.In addition,in complex decision-making problems,the strategy sets of decision makers are often constraint,the proposed constraint strategy game with its solution algorithm,CSG-LL algorithm,will provide a powerful tool for such problems.
Fig.6.The attack methods of R and B according to the Nash equilibrium strategy.
Fig.7.Comparison of the CSG-LL algorithm and traditional algorithm.
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to in fluence the work reported in this paper.
This work was supported by Major Projects for Science and Technology Innovation 2030(Grant No.2018AA0100800),Equipment Pre-research Foundation of Laboratory (Grant No.61425040104)and in part by Jiangsu Province“333”project under Grant BRA2019051.




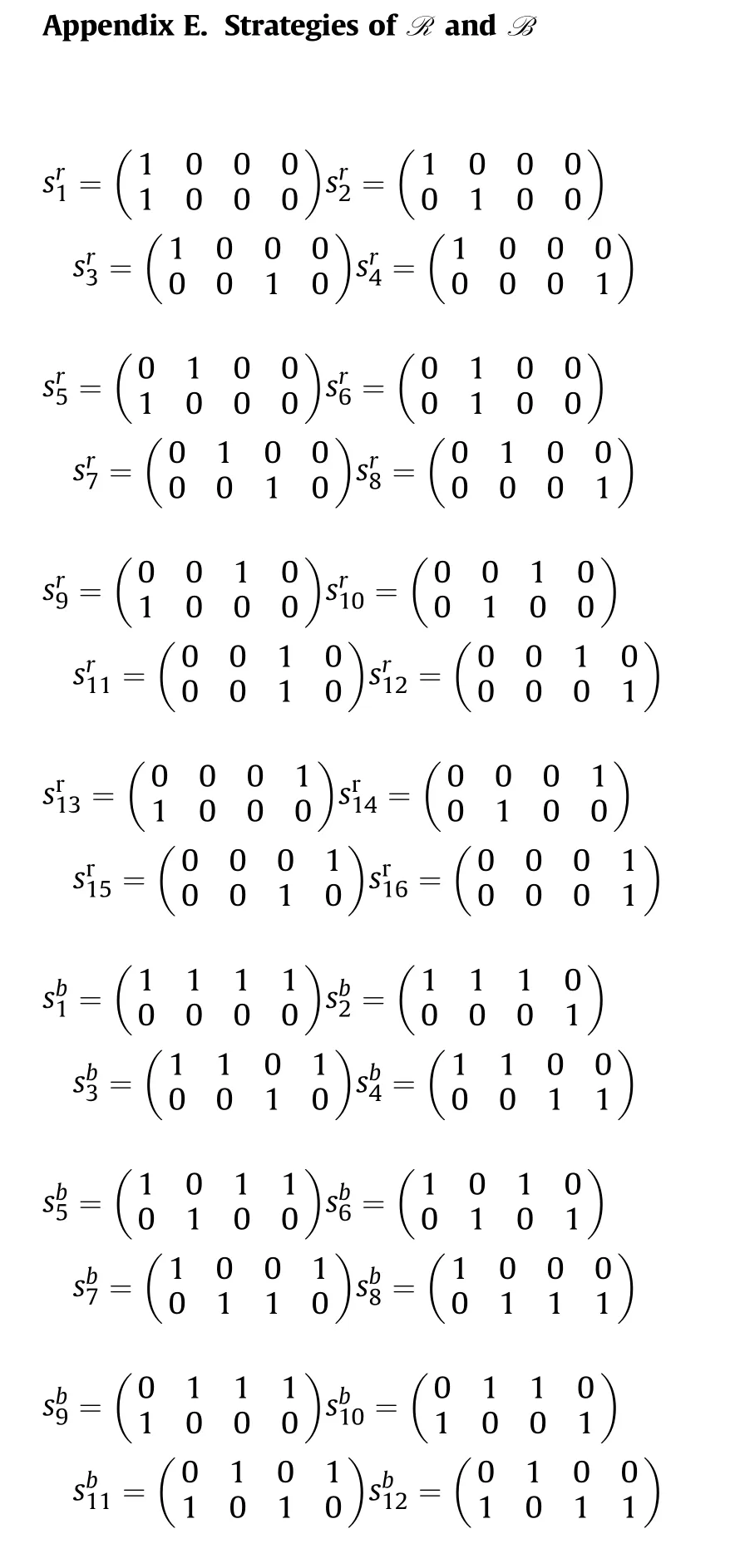
杂志排行
Defence Technology的其它文章
- High explosive unexploded ordnance neutralization-Tallboy air bomb case study
- Dynamics and rebound behavior analysis of flexible tethered satellite system in deployment and station-keeping phases
- Finite element analysis of functionally graded sandwich plates with porosity via a new hyperbolic shear deformation theory
- Investigation on the penetration of jacketed rods with striking velocities of 0.9-3.3 km/s into semi-in finite targets
- The effect of strain rate on compressive behavior and failure mechanism of CMDB propellant
- Adaptive target and jamming recognition for the pulse doppler radar fuze based on a time-frequency joint feature and an online-updated naive bayesian classi fier with minimal risk
