Investigation on the penetration of jacketed rods with striking velocities of 0.9-3.3 km/s into semi-in finite targets

Kui Tng ,Jin-xing Wng ,*,Hi-ping Song ,Nn Zhou

a National Key Laboratory of Transient Physics,Nanjing University of Science and Technology,Nanjing,210094,China

b China North Vehicle Research Institute,Beijing,100072,China

c Department of Criminal Science and Technology,Nanjing Forest Police College,Nanjing,210023,China

Keywords:Jacketed rod Semi-in finite target Damage mechanism Penetration performance

ABSTRACT In this study,a combined experimental,numerical and theoretical investigation is conducted on the penetration of semi-in finite 4340 steel targets by a homogeneous 93W rod and two types of jacketed rods with striking velocities of 0.9-3.3 km/s.The results show that the jacketed rods produced typical“co-erosion”damage at all test velocities,except for the 93W/1060Al jacketed rod,which switched from an early“bi-erosion”damage to later“co-erosion”damage at a striking velocity of 936 m/s.However,the homogeneous 93W rod always forms a large mushroom head during the penetration process.The damage mechanisms of these two types of jacketed rods differ for striking velocities of 0.9-2.0 km/s,but this difference gradually decreases with increased striking velocity.For velocities of 2.0-3.3 km/s,all three types of projectiles exhibit typical hydrodynamic penetration characteristics,and the damage mechanisms of the two types of jacketed rods are almost identical.For the same initial kinetic energy,the penetration performance of the jacketed rods is distinctly superior to that of the homogeneous 93Wrods.Compared with jacket density,jacket strength shows a more signi ficant in fluence on the damage mechanism and penetration performance of the jacketed rod.Finally,an existing theoretical prediction model of the penetration depth of jacketed rods on semi-in finite targets in the co-erosion mode is modi fied.It transpires that-in terms of penetration depth-the modi fied theoretical model is in good agreement with the experimental and numerical observations for 93W/TC4 and 93W/1060Al jacketed rods penetrating semi-in finite 4340 steel targets.

1.Introduction

To maintain the structural integrity of the long rod projectile during acceleration and free flight,the addition of an envelope around the slender cylinder-forming a so-called“jacketed penetrator”[1-9]-to augment its stiffness under flexure has been suggested.And,a series of experiments and numerical simulations have been conducted to examine the ballistic performance of such jacketed rods.Lehr et al.[3]experimentally investigated the terminal ballistic ef ficiency of jacketed rods made of WHA with carbon-fiber reinforced plastic(CFRP[10])and 1006 steel envelopes.A combined numerical and experimental study on the penetration of jacketed rod penetrators into steel plates was carried out by Andersson and Ottosson[2],as well as by Pedersen et al.[4].In the former study,a CFRP-jacketed WHA penetrator was considered,with striking velocities of approximately 1.6 km/s.WHA cores surrounded by 1006 steel and 4130 steel jackets with core diameter-to-jacket thickness ratios of 0.4 and 0.6 were studied by Pedersen et al.[4],their striking velocity was controlled within the range 2.1-2.3 km/s.In addition,Peskes and Lanz[5]performed an experimental study to assess the terminal ballistic performance of WHA long-rod penetrators featuring steel and titanium jackets;the impact velocities tested were within the range of 1.5-1.7 km/s.Cullis and Lynch[6]experimentally studied the effects of jacket thickness on the penetration performance of an EN24 steeljacketed WHA penetrator at striking velocities of approximately 1.6 km/s and 2.2 km/s.In terms of theoretical research,an analytical model of the cratering process triggered by the high-velocity penetration of a jacketed rod into a metal target was developed by Lee[7].Furthermore,Sorensen et al.[8]developed a generalized penetration model for a jacketed rod.Wen et al.[9]also developed an analytical model of cratering and predict the depth of penetration(DOP)of jacketed rods in semi-in finite targets.Notably,in almost all these experiments,the striking velocity was controlled within a very small range that is close to 1.6 km/s or 2.2 km/s.Experimental data suitable for verifying the prediction accuracies of the above theoretical models are notably lacking.Moreover,only a few types of jacket materials(e.g.CFRP and steel)were considered in these tests.Thus,it is necessary to collect more experimental data for comparison and veri fication,especially experimental data at a larger striking velocity span.

In the present paper,a combined experimental,numerical,and theoretical study on the damage mechanism and penetration performance of jacketed rods penetrating semi-in finite 4340 steel targets is presented.The range of striking velocities is extended to cover a continuous interval of 0.9-3.3 km/s,and two types of jacketed long rods,featuring two novel jacket materials(1060 aluminum and TC4 titanium alloy),are investigated.

2.Experimental procedure

Fig.1 depicts the geometry of the homogeneous 93W-4.9Ni-2.1Fe(93W)rod and the jacketed rod.Both rods feature a spherical nose and have the following dimensions:total length L=70 mm,outside diameter(D)=7 mm,and core diameter(d)=5 mm.The jacketed rod consists of a central 93W rod surrounded by a Ti-6Al-4V alloy(TC4)or 1060 aluminum jacket.The core and jacket are bonded by shrinking through the application of shaft/hub assembly.The Ti-6Al-4V alloy has a high elastic modulus and low density;it provides a suf ficient bending stiffness and is lightweight.Thus,it was selected as one of the jacket materials.In addition,the damage mechanism and penetration performance of jacketed rods is unclear for cases in which both the density and strength of the jacket material are low.Therefore,1060 aluminum was selected as the second jacket material.

Three types of projectiles were tested:a homogeneous 93Wrod projectile and 93W/1060Al and 93W/TC4 jacketed rod projectiles.These projectiles were tested by a 25-mm powder gun and a 25-mm calibre,two-stage light-gas gun.Fig.2 illustrates the projectiles and sabots used by the powder gun.The striking velocities were varied within the range 897-3276 m/s.And,semi-in finite 4340 steel targets were used.The material properties of the projectile and target materials are listed in Table 1.Table 2 summarises the penetration data from the three series of experiments.

3.Experimental results and discussions

As shown in Table 2,the DOP of the homogeneous 93Wrods and 93W/TC4 jacketed rods can be seen to monotonically increase with increasing striking velocities.However,the DOP of the 93W/1060Al jacketed rod decreases sharply when the striking velocity is approximately 3.2 km/s,due to the projectile bending-and even fracturing-before impact.It can be seen from Fig.3(a)that the 93W/1060Al jacketed rod is bent.And,the 93W/1060Al jacketed rod fractures,as shown in Fig.3(b).The results given in Fig.3(a)and(b)also indicate that although the L/d ratio of the 93W jacketed rod’s core is only 14,it still suffers from structural instability or even destruction when the striking velocity reaches 3.2 km/s.However,at a striking velocity of 3276 m/s,the 93W/TC4 jacketed rod exhibits no structural integrity problems,as shown in Fig.3(c).It is evident that adding a TC4 jacket to the slender cylinder augments the stiffness under flexure.

Table 1 Material properties.

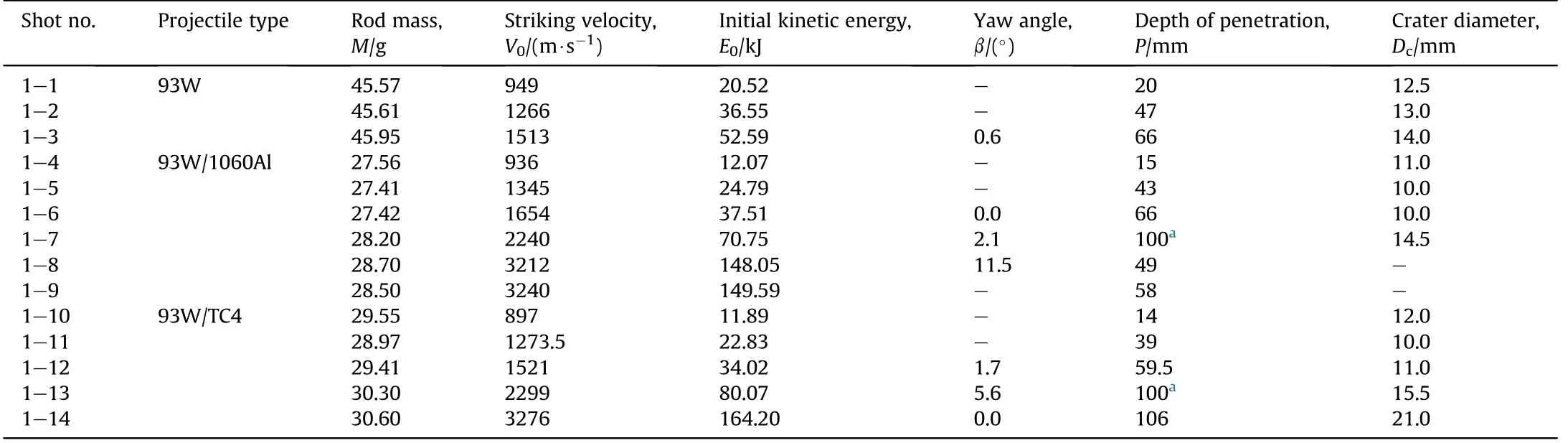
Table 2 Data summary for projectiles and targets.

All the sectional views of the targets are presented in Figs.4-6.As shown in Fig.4,the DOP can be seen to monotonically increase as the striking velocity increases.In these three cases,the trajectory is straight and smooth.The bottom of the ballistic hole is approximately semi-spherical.Correspondingly,a signi ficant mass erosion occurred for these 93W rods.The majority of rod bodies with an original length of 70 mm were eroded,with only a small number of 93Wfragments retained;for example,see Shots 1-1(Fig.4(a)).The fragments were predominately produced when the eroded material underwent reverse flow and then froze up.

As shown in Fig.5(a)-(c),all 93W/1060Al jacketed rods were signi ficantly eroded,with their jackets almost completely eroded.Only a 93Wmushroom head and a small number of fragments were retained,as shown in Fig.5(b)and(c).At a striking velocity of 936 m/s,the residual 93Wcore did not form a mushroom head but was bent near the tip owing to the projectile yaw.At a striking velocity of 2240 m/s,the 93W/1060Al jacketed rod perforated a single layer,100-mm thick 4340 steel target,and the penetration channel was curved because of the small angle of attack.The petalling and tensile failure of the target can be clearly observed,and the transverse crack(caused by tension)is visible.At striking velocities of 3212 m/s and 3240 m/s,the trajectory shapes were irregular because the projectiles were bent or fractured before penetrating the targets.

Fig.1.Geometries of the rod projectiles.

Fig.2.Photographs of the sabots and projectiles used by the powder gun.

It can be seen from Fig.6 that at a striking velocity of 897 m/s,there is a straight and smooth trajectory;however,the residual rod was absent.Fig.7 shows the pro files of two different states of a jacketed rod penetration,i.e.co-erosion and bi-erosion[9].When co-erosion occurs,the jacketed rod penetrates as well as the core,and the jacket material does not interact with the target directly due to the debris of the core flowing in reverse direction,as shown in Fig.7(a).Otherwise,the jacketed rod is in bi-erosion state,as shown in Fig.7(b),where two different stagnation points are observed,due to the independent interaction of the core and jacket materials with the target.At V=1273.5 m/s,a“co-erosion”[9]penetration mode was observed,and the residual 93W core exhibited a heavy bulge.Large numbers of 93Wand TC4 fragments underwent reverse flow and then froze up in the penetration channel.At a lager striking velocity of 1521 m/s,signi ficant mass erosion occurred for the jacketed rod and only a small number of fragments were retained,and the penetration channel was curved.The shape of the penetration channel of Shot 1-13 was almost identical to that of Shot 1-7.At the much higher striking velocity of 3276 m/s,the diameter of the penetration channel is pretty large,and the jacket and the core were completely eroded.

Fig.3.Flight attitudes captured by high-speed camera.

Fig.4.Post-test longitudinal section of 4340 steel targets fired with homogeneous 93Wrods.

According to the experimental results,the DOPs and crater diameters of the homogeneous 93Wrods exceeded those of the two types of jacketed rods when the striking velocities were approximately identical.Once penetrated by jacketed rod projectiles,the failure of the projectiles and targets for yawed and normal penetration was drastically different,see Shots 1-6 and 1-7.In addition,because the range of striking velocities was large,and the experiments were limited by test costs,only a few velocities were investigated.The damage mechanism and penetration performance of the projectiles cannot be accurately analysed via the test results alone.Therefore,the penetration of these three types of projectiles into 4340 steel targets was further analysed via numerical simulation.

Fig.5.Post-test longitudinal section of 4340 steel targets fired with 93W/1060Al jacketed rods.

Fig.6.Post-test longitudinal section of 4340 steel targets fired with 93W/TC4 jacketed rods.

4.Numerical simulation

4.1.Numerical simulation model and veri fication

To obtain suf ficient data for the analysis of the damage mechanisms of the homogeneous 93Wrod and jacketed rods,AUTODYN was adopted to simulate the penetration process.The Smooth Particle Hydrodynamics(SPH)method[11,12]was employed for the projectile.Thus,the relevant projectile materials(93W,TC4,and 1060Al)did not use failure models.Meanwhile,a Lagrange solver was employed for the target to improve the computing ef ficiency.For all the materials 1060Al,TC4,4340 steel and 93W,the SHOCK[13]equation of state(EoS)was used.The Johnson-Cook[14]and Steinberg[9]constitutive models were used.The speci fic parameters for 93W[15]and 4340 steel[16]are listed in Table 3.In addition,the Johnson-Cook failure model[17]was employed for the 4340 steel,and the corresponding parameters[16]are listed in Table 4.For the details of the Johnson-Cook and Steinberg constitutive models,SHOCK EoS,and Johnson-Cook failure model,see Appendix.The speci fic parameters for TC4 and 1060Al are listed in Table 5.The parameters for 1060Al were obtained by fitting the test data reported in Ref.[18].The Lagrange element had a minimum size of 0.25 mm,and the SPH particles had a diameter of 0.125 mm.The numerical simulation model for a 4340 steel target penetrated by a jacketed rod is shown in Fig.8.

The experimental and numerical simulation results for three different conditions are compared in Fig.9,and the corresponding DOP and crater diameter data are listed in Table 6.It is seen that the numerical results agree well with the experimental results.In addition,the experimentally and numerically obtained morphologies of the residual rod for both Shots 1-6(Due to the deviation in cutting the front target,resulting in the experimental crater diameter seems to be much smaller than the simulation result.The actual results are given in Table 6)and 1-11 are almost identical.

Fig.7.Two typical damage modes of the jacketed rod[9].

4.2.Numerical simulation results and discussion

In this section,the damage mechanisms of these three types of projectiles are analysed.The numerical results for the three types of projectiles penetrating 4340 steel targets normally at three striking velocities(low,medium and high),are listed in Table 7.

The typical morphologies of the three types of projectiles during penetration,under initial striking velocities close to 940 m/s,are shown in Fig.10.It can be seen that the deformation of the head of the homogeneous 93Wrod is similar to that of the core of the 93W/1060Al jacketed rod.The head deformation of the 93W/TC4 jacketed rod core differs signi ficantly from the other two in that a prominent bulge can be seen near its head.Particularly,for the 93W/1060Al jacketed rod with striking velocity V=936 m/s,the damage mode changes from bi-erosion[9]during early stage to coerosion[9]during later stages of penetration,as shown in Fig.11.This has not been observed in previous experiments or numerical simulations.The nose(penetration velocity)and tail velocity history curves for these three types of projectiles,at striking velocities close to 940 m/s,are presented in Fig.12(a).It can be seen that the penetration velocity of the 93W homogeneous rod is the largest,and that of the 93W/TC4 jacket rod is the smallest.However,compared to the 93W/TC4 jacket rod,the penetration velocity of the 93W/1060Al jacket rod is only slightly lower than that of the homogeneous 93W rod.In terms of tail velocity,that of the 93W/TC4 jacket rod decays the fastest,followed by the 93W/1060Al jacketed rod,with the homogeneous 93W rod decaying slowest.The penetration velocity of the 93W/TC4 jacketed rod is the smallest,and its tail velocity decay rate is the largest;thus,the DOP is much smaller than that of the other projectiles,as shown in Table 7.Because the penetration and tail velocity decay rates of the 93W/1060Al jacket rod are only slightly lower than those of the homogeneous 93Wrod;this results in the former’s DOP being very close to that of the latter,as shown in Table 7.

Table 3 Material parameters for Johnson-Cook constitutive model and SHOCK EoS.

Table 4 Damage parameters of 4340 steel[16].

With the exception of the 93W/1060Al jacketed rod penetrating targets at striking velocity of 936 m/s,only the“co-erosion”damage mode is observed for the two types of jacketed rods.Under initial striking velocities close to 1520 m/s,the mushroom heads are typically formed from the cores of the two jacketed rods;however,the transition zone between the undeformed rear and the head of the core for the 93W/1060Al jacketed rod is much shorter than that of the 93W/TC4 jacketed rod,as shown in the boxes in Fig.13.Furthermore,a comparison of Fig.10(c)and 13(c)indicates that the deformation degree(i.e.,the length and diameter)of the transition zone for the 93W/TC4 jacketed rod decreases with increasing striking velocity.As shown by the oval in Fig.13(b),the 1060 aluminum jacket also exhibits a large range of deformations under the action of the reversely flowing core debris.It is clear that the length of the undeformed rear of the core is much larger than that of the jacket.However,the length of the undeformed rear of the TC4 jacket is almost identical to that of the core.The morphology of the 93W projectile shown in Fig.13(a)indicates that the 93W jacket cannot be easily ejected by the reversely flowing core debris(if the 93Whomogeneous rod projectile is equivalent to a jacketed rod projectile with a 93Wjacket),because the strength and density of the jacket are identical;thus,a much larger“mushroom head”and penetration channel were formed,and the transition zone of the core was the shortest.The penetration and tail velocity history curves of the three types of projectiles,under striking velocities close to 1520 m/s,are shown in Fig.12(b).It can be seen that the relationship between these three projectiles’velocity curves are identical to those obtained under striking velocities close to 940 m/s.The above discussion shows that the damage modes of the two jacketed rods are identical at striking velocities of about 1520 m/s,though their damage mechanisms are signi ficantly different.

The three types of projectiles present typical hydrodynamic penetration characteristics at increased striking velocities exceeding 2.0 km/s-for instance,at an initial striking velocity of approximately 3.2 km/s,the penetration processes are shown in Fig.14.The projectile fragments flow radially and reversely,resulting in an approximately hemispherical crater bottom.The crater diameter is approximately three times larger than the original diameter of the rod.As shown in Table 7,the DOPs and crater diameters of the two types of jacketed rod projectiles are almost identical;furthermore,their damage mechanisms are almost identical.The penetration and tail velocity history curves of the three types of projectiles,at striking velocities close to 3.2 km/s,are given in Fig.15.In the range of 0-50μs,the velocity curves of the three projectiles coincide very closely.Above 50μs,the penetration and tail velocity decay rates for the two jacketed rods exceed that of the homogeneous 93Wrod.

Table 5 Material parameters for Steinberg constitutive model and SHOCK EoS.

Fig.8.Meshed numerical simulation model.

Fig.9.Cross-sectional comparisons of experimental and simulated results for three types of projectiles.

Table 6 Comparisons of experimental and numerical results for three types of projectiles.

Table 7 Numerical results for the three types of projectiles at three typical velocities.

To summarise,when the striking velocity is within 0.9-2.0 km/s,the 93W rod forms a mushroom head during penetration.The damage mode of the 93W/1060Al jacketed rod changes from the earlier“bi-erosion”to the latter“co-erosion”mode at a striking velocity of 936 m/s;however,at higher striking velocities,only the“co-erosion”mode is observed.For the 93W/TC4 jacketed rod,only the“co-erosion”mode is observed across the entire striking velocity range.The damage mechanisms of the two types of jacketed rods in this striking velocity range are notably different;however,this difference gradually decreases with increasing striking velocity.For striking velocities in the range of V=2.0-3.3 km/s,all projectiles exhibit typical hydrodynamic penetration characteristics,and the damage mechanisms of the two types of jacketed rods are almost identical.

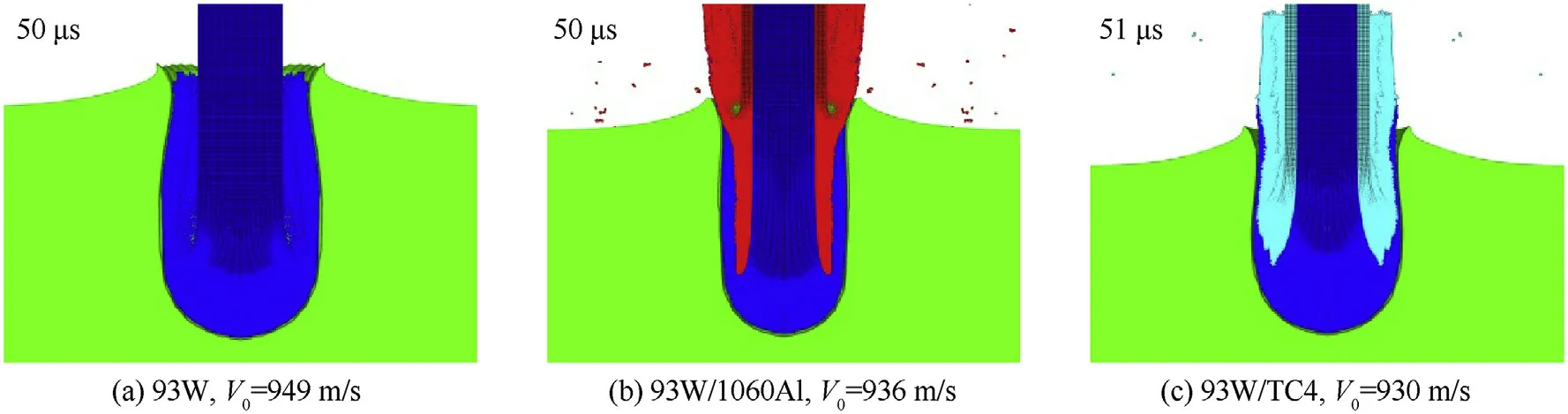
Fig.10.Morphologies of three types of projectiles during the penetration process.

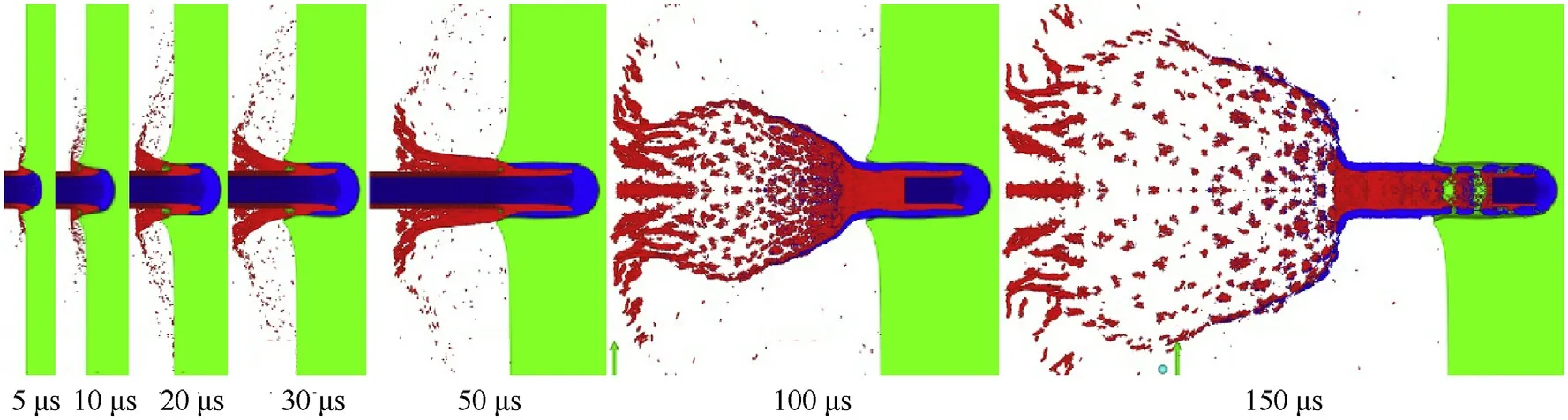
Fig.11.Numerical results for 93W/1060Al jacketed rod penetrating 4340 steel target at striking velocity of 936 m/s.

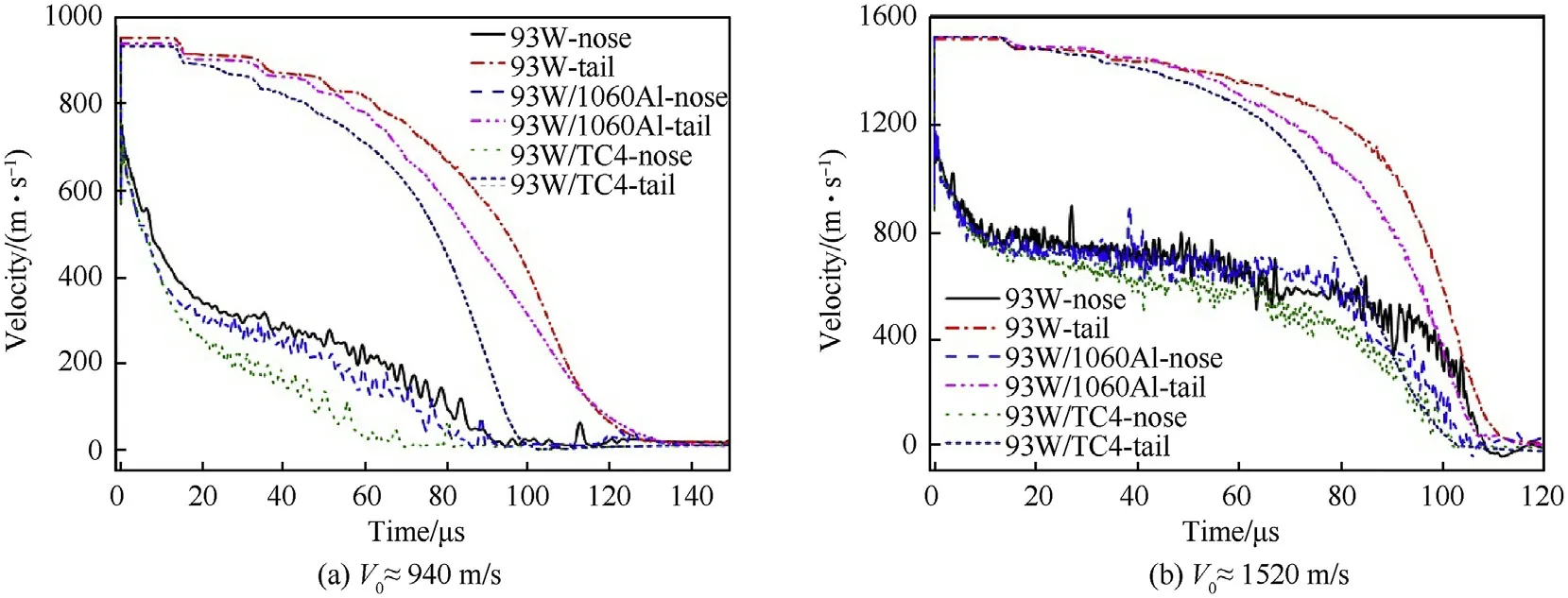
Fig.12.Nose and tail velocity history curves for three types of projectiles.

Fig.13.Morphologies of three types of projectiles at 50μs.

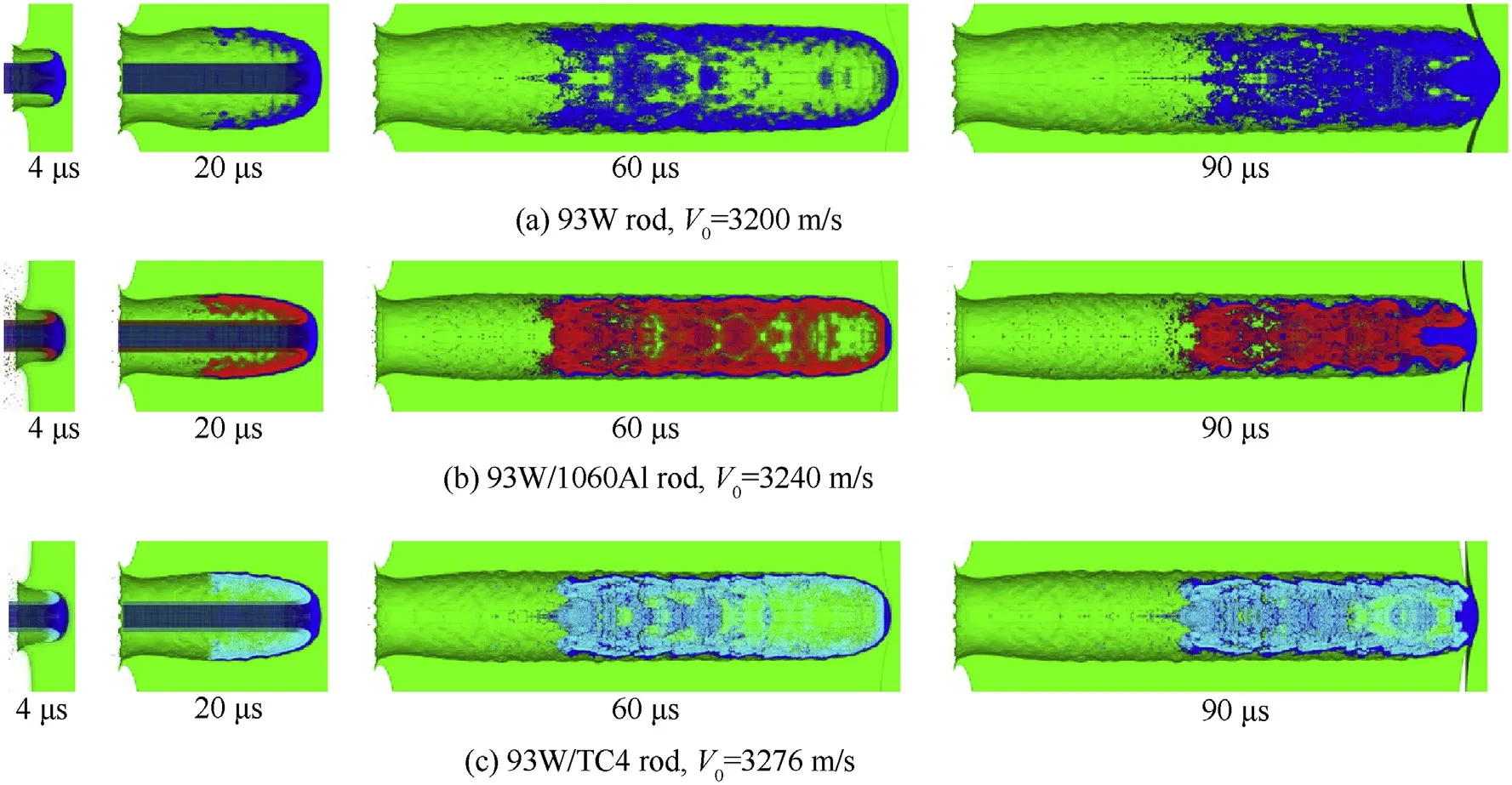
Fig.14.Penetration processes for three types of projectiles penetrating 4340 steel targets at V0≈3200 m/s.

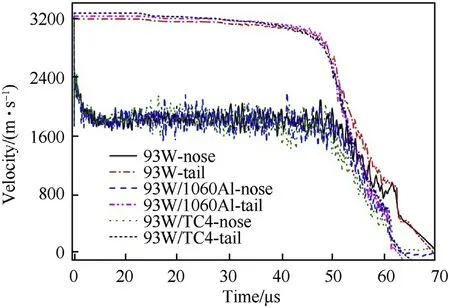
Fig.15.Nose and tail velocity history curve of three types of projectiles for V0≈3200 m/s.

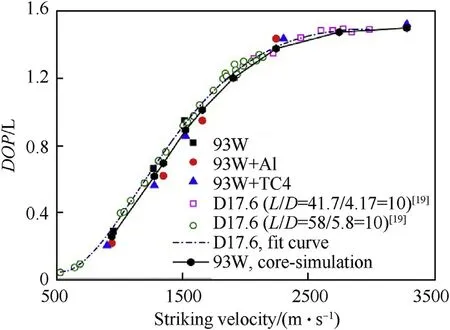
Fig.16.Normalised DOP for homogeneous 93Wrods and jacketed rods with respect to striking velocity.

5.Analysis of penetration performance

5.1.In fluence of striking velocity

The experimental data obtained in this study for the 93W homogeneous rod were limited;thus,the data collected by Hohler and Stilp[19]is cited for comparison.The two sets of experimental(L/D=10)data given by Hohler and Stilp[19]were curve fitted and are identical as denoted by the dashed line in Fig.16.The experimental data obtained in the present study are on the fitted curve,and agree well with the experimental results from Hohler and Stilp[19].As shown in Fig.16,when the striking velocity is below 1.7 km/s,all experimental data for jacketed rods are below the fitted curve,indicating that the penetration performance of the jacketed rods is less than that of the homogeneous 93W rod.When the striking velocity exceeds 2.0 km/s,the penetration performance of the 93W/TC4 jacketed rod is identical to that of the homogeneous 93W rod.

The original objective of the jacketed rod project was to solve the flight stability and structural integrity problems experienced by projectiles with large aspect ratio.Therefore,the penetration performance of the jacketed rod was compared with that of the homogeneous 93Wcore.The results for the homogeneous 93Wcore rod were obtained numerically and are denoted by the solid line with solid hexagon icons in Fig.16.There,the penetration performance of the homogeneous 93Wcore rod(L/D=70/5=14)can be seen to be less than that of the homogeneous 93Wrod(L/D=70/7=10),which agrees well with the“L/D effect”[20,21]and veri fies the validity of the simulation results.Through comparison,it can be seen that the penetration performance of the jacketed rods is only slightly lower than that of the homogeneous 93W core rod for striking velocities below approximately 1.7 km/s,whereas the former outperforms the latter for striking velocities exceeding 2.0 km/s.In Ref.[4],the experimental results also indicated that the penetration performance of the 91%tungsten alloy/4130 steel jacketed rod is slightly better than the all-tungsten baseline rod of the same exterior dimensions,at a nominal impact velocity of 2.2 km/s.

5.2.In fluence of initial kinetic energy

As shown in Fig.17,both the experimental and numerical results indicate that the penetration performance of the jacketed rods is notably superior to that of the 93Wrods.For example,at an initial kinetic energy of E=36.55 kJ,the DOP of the 93W/1060Al jacketed rod is 43.5%greater than that of the 93Wrod.For kinetic energies of E=12-40kJ,the experimental results show that the penetration performance of the 93W/1060Al jacketed rod is nearly identical to that of the 93W/TC4 jacketed rod,and the DOP/L increases linearly with increasing kinetic energy.However,the numerical results indicate that the penetration performance of the 93W/1060Al jacketed rod is better than that of the 93W/TC4 jacketed rod.This may be because not all jacketed rods impacted normal to the target,in contrast to the numerical simulations in which all projectiles achieved normal penetration.For a kinetic energy of E＞40 kJ,the increase in the DOP gradually slows and eventually approaches a limit.The 93W/1060Al jacketed rod reaches this limit with the smallest kinetic energy,whereas the 93W rod does so with the largest.

5.3.In fluence of jacket material properties

In this Section,the in fluence of the yield strength and density of the jacket is analysed,predominately through numerical simulations.In the numerical simulations,using the constitutive model parameters for the 1060 aluminum jacket(given in Table 5),the yield strengthσof the jacket was modi fied to 0.4 GPa,0.8 GPa,and 1.6 GPa,and the correspondingly maximum yield strengthσwas modi fied to 0.48 GPa,0.98 GPa and 1.78 GPa,respectively.A striking velocity of 1654 m/s was considered.

The morphologies of the jacketed rod projectiles with different jacket strengths at 50μs are given in Fig.18.Clearly,when the jacket strength increased from 0.04 GPa to 0.4 GPa,the transition zone between the undeformed rear and the head of the core(denoted by the square box)was dramatically increased.The sizes of the transition zones were almost unchanged for a jacket strength increase of 0.4 GPa-1.6 GPa.However,the deformation range of the jacket(marked by the oval)gradually decreased with increasing jacket strength.It can be seen from Fig.20(a)that the crater diameter of the jacketed rod increases with an increase in jacket strength,but the DOP gradually decreases.The resistance of the jacket acted on the reversely flowing core fragments increased with increasing jacket strength,resulting in more signi ficant radial movement of these core fragments,and therefore a larger crater diameter.As shown in Fig.19,the penetration(head)velocity of the jacketed rod projectile decreased with increasing jacket strength.The decrease in penetration velocity will inevitably cause a decrease in DOP.It can be seen from Fig.20,when the jacket strength increased from 0.4 GPa to 0.8 GPa,the DOP decreased signi f icantly,from 68.8 mm to 62.00 mm.Clearly,the jacket strength has a signi f icant in f luence on the penetration performance of the jacketed rod.

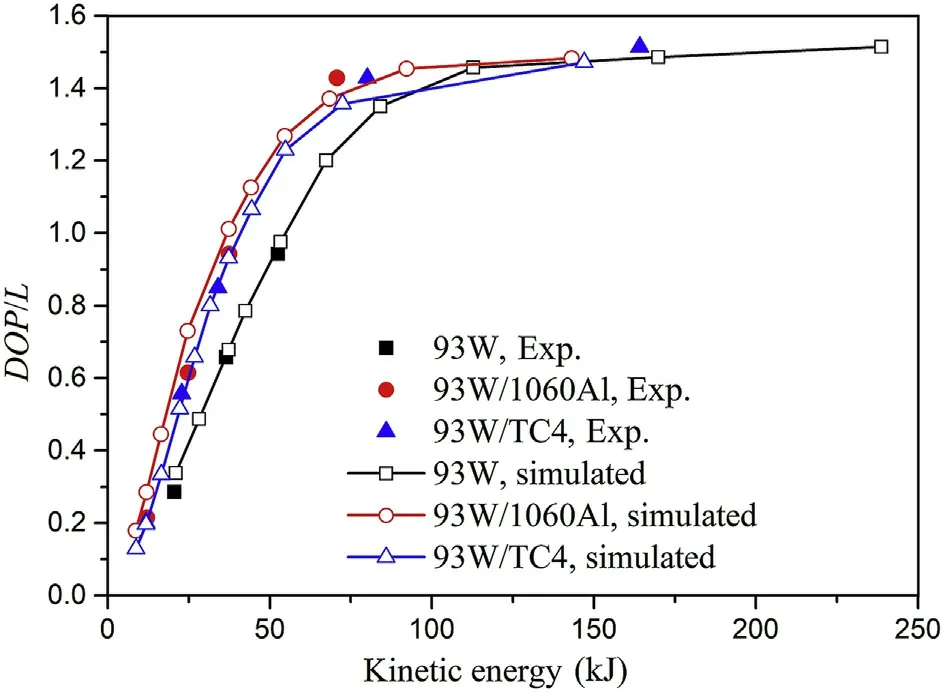
Fig.17.Normalised DOP for three types of projectiles with respect to initial kinetic energy.

The in fluence of the jacket density on the penetration performance of the projectile was also investigated.In the numerical simulations,using the model parameters for the 1060Al jacket,the yield strengthσand maximumyield strengthσof the jacket were set to 0.8 GPa and 0.88 GPa,respectively.Densities of 2.71 g/cm,5.27 g/cm,6.55 g/cm,and 7.83 g/cmwere considered,as well as striking velocities of 1654 m/s and 2000 m/s.The damage modes as well as the penetration and tail velocity of jacketed rods with different jacket densities are almost identical.It can be seen from Fig.20(b)that both DOP and crater diameter show a monotonic increase with increasing jacket density.However,the DOP increased by only 3 mm for a jacket density increase going from 2.71 g/cmto 7.83 g/cm.Compared with the DOP,the crater diameter increased dramatically under an increase in jacket density.The above analysis demonstrates that both the damage mechanism and penetration performance of jacketed rods are in fluenced by the density of the jacket.However,the in fluence is almost negligible.

Thus,in terms of the jacket strengths and densities,it can be concluded that the in fluence of jacket strength on the damage mechanism and penetration performance of the jacketed rod is signi ficant;speci fically,the smaller the strength of the jacket,the better the penetration performance of the projectile.In Ref.[7],the author pointed out that due to the low-density jacket,a smaller crater diameter is observed compared with the homogeneous rod of identical aspect ratio.This conclusion is very consistent with the results obtained experimentally and numerically in the present paper.However,in the present paper,we found that the crater diameter is not only in fluenced by the jacket density,but also the jacket strength.

Comprehensive consideration on the in fluence of the jacket strength and density,striking velocity,and kinetic energy on the damage mechanism and penetration performance of the jacketed rod,for a jacketed rod with fixed r/r,show that it is preferable to use jacket materials of a lower density and strength,and an elastic modulus that provides the lowest required stiffness under flexure.The in fluence of the jacket density on the penetration performance is almost negligible,and for a speci fic launch system,the smaller the total mass of the projectile,the greater the launch speed,resulting in the better penetration performance.Therefore,it is preferable to use jacket material of a smaller density.As for the jacket strength,it has a signi ficant in fluence on the penetration performance,and the smaller the strength of the jacket,the better the penetration performance of the projectile.Clearly,a small jacket strength is more preferable.In addition,it is very important that the jacket must be able to provide suf ficient bending stiffness for the slender core.The ending stiffness is given as EI,where E is the elastic modulus of the material and I is the moment of inertia.For a jacketed rod with fixed r/r,the moment of inertia of its jacket is also a constant,thus a suitable jacket material elastic modulus is very important.

6.Penetration model

According to the analytical model given by Wen et al.[9],when co-erosion occurs(Fig.21),at any time t during penetration,the erosion rate and the momentum balance for the undeformed rear of the jacketed rod are given as

Fig.18.Morphologies of jacketed rod projectiles with different jacket strengths at 50μs.

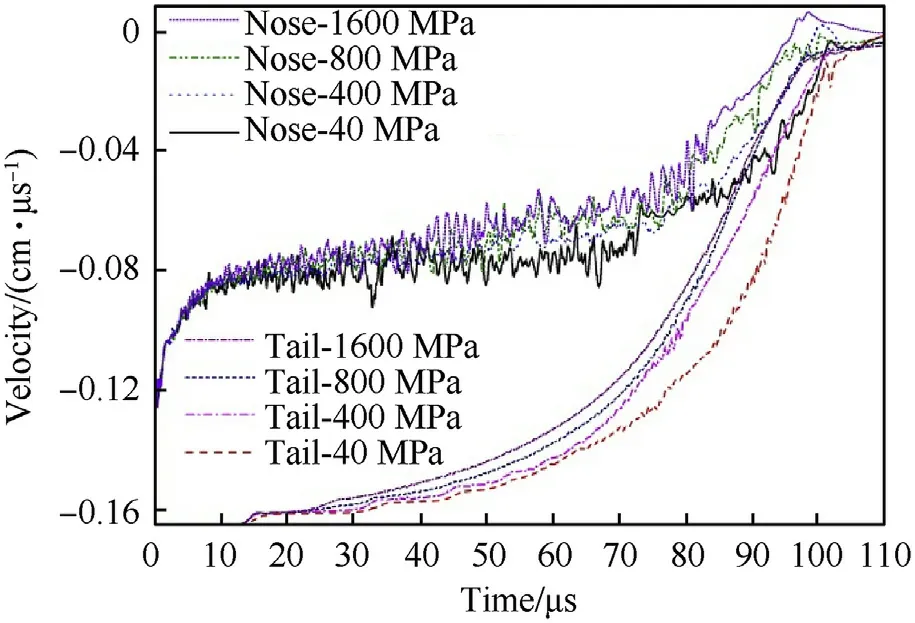
Fig.19.Nose and tail velocity history curves of jacketed rod projectiles with different jacket strength.

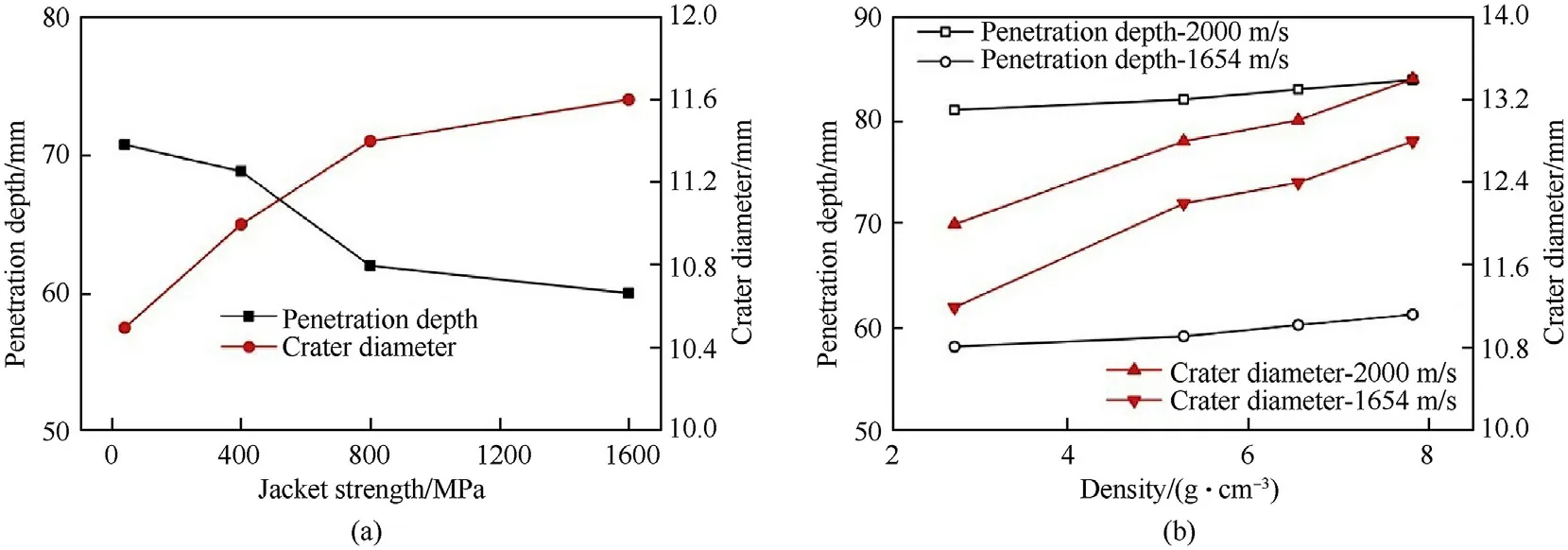
Fig.20.DOP and crater diameter of jacketed rod projectiles with different jacket(a)strengths and(b)densities.

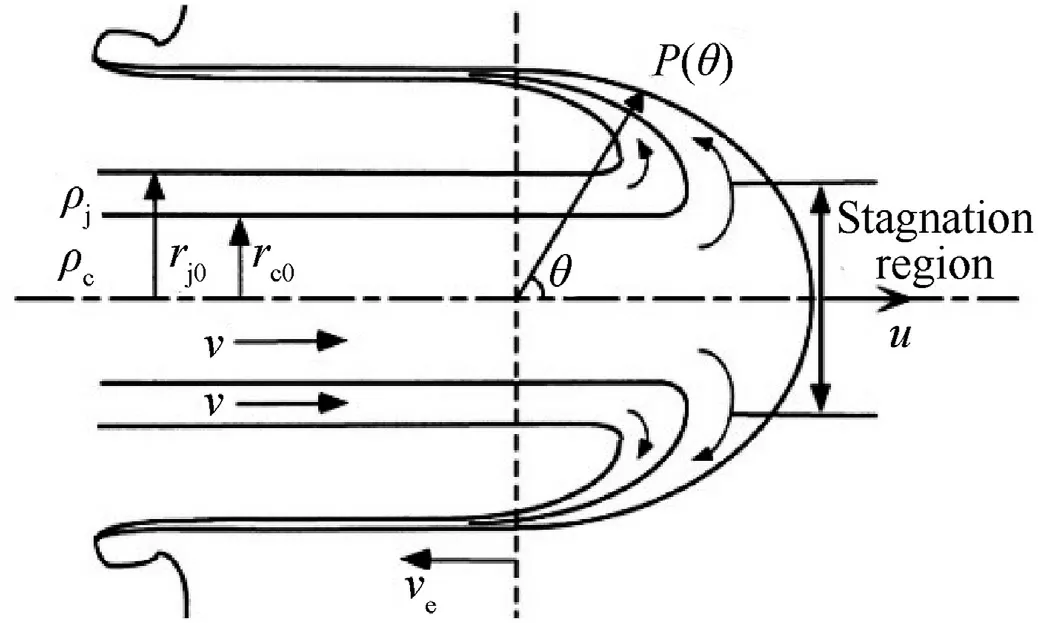
Fig.21.Schematic diagram of co-erosion occurrence for a jacketed rod penetrating a semi-in finite target.

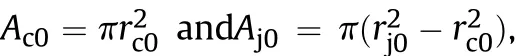
In Sections 4.2 and 5.3,the in fluence of the jacket strength and density on the damage mechanism and penetration performance of the jacketed rod was analysed;it was found that the in fluence of the jacket strength is more signi ficant.In Fig.18,it can be seen that when the strength of the jacket is much lower than that of the core,the length of the undeformed rear of the jacket is much shorter than the core length.The closer the jacket and core strengths are to each other,the closer the lengths of the undeformed rear of the jacket and the core;that is,at any time t during the penetration

process,the lengths of the undeformed rear of the jacket and the core of the jacketed rod cannot be modelled as the same parameter.However,only one parameter pertaining to the length of the undeformed rear of the projectile is used in the aforementioned theoretical model:the parameter l.This parameter appears in both Eqs.(1)and(2);it tends to represent the length of the undeformed rear of the core.Hence,only the parameter A-appearing in Eq.(2)-is incompatible with the other parameters,because the length of the undeformed rear of the jacket is less than l.To make the physical meaning of Eq.(2)more consistent with the actual situation,the concept of the effective cross-sectional area of the jacket is proposed and introduced into Eq.(2),as follows:

where Vis the tail velocity of the projectile when the penetration velocity is zero.

For the jacketed rods investigated in this study,most of the material parameters for the relevant projectiles and targets are given in Tables 3 and 5 However,according to Wen et al.[9],to a first approximation,Hugoniot Elastic Limit(HEL)is taken as the dynamic strengths of the core(Y)and jacket(Y).And,Hugoniot Elastic Limit is calculated by HEL=Y(1-υ)/(1-2υ),where Y is the yield stress in a bilinear material model,υis the poisson’s ratio.Herein,based on the constitutive model parameters used in the numerical simulation,we fitted the yield stress corresponding to the bilinear model of the projectile and target materials.Under the quasi-static condition,the Johnson-Cook constitutive model degenerates into

The quasi-static stress-strain curves and fitted curves for bilinear model are shown Fig.22,and the yield stress corresponding to the bilinear model for 93W,TC4,1060 Al,and 4340 steel are obtained and listed in Table 8.

In addition,the bulk modulus K,the shear modulus G,the flow stress Y,and the material parameter k for the 4340 steel target were 159 GPa,81.8 GPa,1090.9 MPa and 1.49,respectively.The WHL model proposed in Ref.[9]was also used to predict the penetration depth of the three types of projectiles.Tables 8 and 9 list the values of some parameters used in the WHL model[9]and the present model,and the predicted results are shown in Figs.23 and 24.

Table 8 Material parameters.

Table 9 Values of some parameters used in WHL model and the present model.

Fig.23 compares the theoretically predicted DOP with the experimental and numerical results for a homogeneous 93W rod penetrating a semi-in finite 4340 steel target.And,Fig.24 compares the theoretically predicted DOP with the experimental and numerical results for two types of jacketed rods penetrating semiin finite 4340 steel targets.It can be seen from Figs.23 and 24 that the present model predictions are in reasonable agreement with the experimental and numerical results for both the homogeneous 93W rod and the jacketed rods.It can be concluded that the modi fied theoretical model is applicable to both homogeneous rod projectiles and jacketed rod projectiles penetrating semiin finite targets.

7.Conclusions

This paper presents a combined experimental,numerical,and theoretical investigation on the damage mechanism and penetration performance of homogeneous 93W rods and two types of jacketed rods penetrating semi-in finite 4340 steel targets,at striking velocities within the range of 0.9-3.3 km/s.

The results show that the two types of jacketed rod presented typical“co-erosion”damage at all test velocities,except for the 93W/1060Al jacketed rod,its damage mode changes from an earlier“bi-erosion”to a later“co-erosion”at a striking velocity of 936 m/s.The homogeneous 93Wrod forms a large mushroom head during penetration.For striking velocities of 0.9-2.0 km/s,the damage mechanisms of the 93W/TC4 and 93W/1060Al jacketed rods were notably different;however,this difference gradually decreased with increasing striking velocity.In the interval V=2.0-3.3 km/s,all three projectile types exhibited typical hydrodynamic penetration characteristics,and the damage mechanisms of the two types of jacketed rods were almost identical.

It was found that the penetration performance of the jacketed rods was less than that of the homogeneous 93W rod for striking velocity below approximately 1.7 km/s,whereas the former outperformed the latter for striking velocities exceeding 2.0 km/s.Under the same initial kinetic energy conditions,the penetration performances of the jacketed rods were distinctly better than those of the homogeneous 93W rods.Compared to jacket density,the jacket strength showed a more signi ficant in fluence on the damage mechanism and penetration performance of the jacketed rods.

Finally,an existing theoretical model for predicting the DOP for jacketed rods penetrating semi-in finite targets in co-erosion mode was modi fied.It transpires that-in terms of penetration depth-the modi fied theoretical model is in good agreement with the experimental and numerical observations for 93W/TC4 and 93W/1060Al jacketed rods penetrating semi-in finite 4340 steel targets.

Fig.22.The quasi-static stress-strain curves and fitted curves for bilinear model.

Fig.23.Comparison of the theoretically predicted DOP with the experimental data and numerical results for a tungsten alloy long rod penetrating semi-in finite 4340 steel targets.

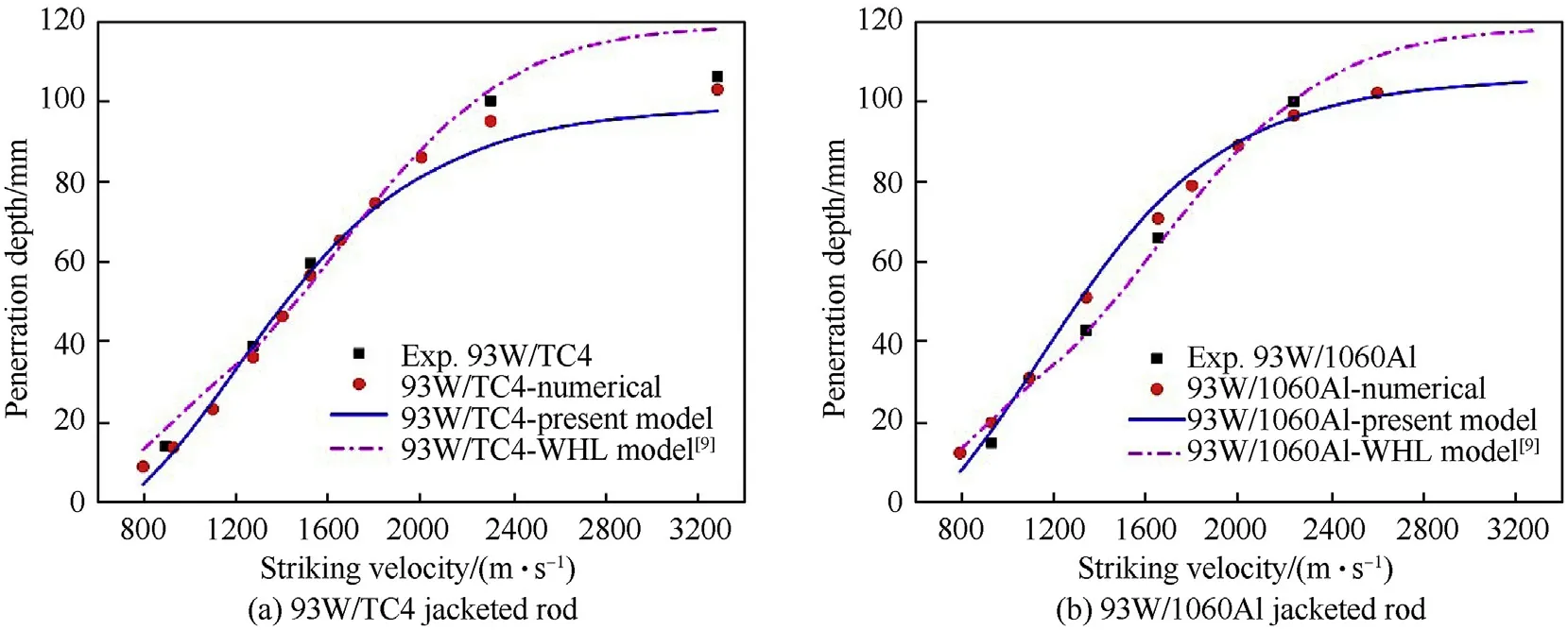
Fig.24.Comparison of the theoretically predicted DOP with the experimental and numerical results for two types of jacketed rods penetrating semi-in finite 4340 steel targets.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to in fluence the work reported in this paper.

This work was supported by the National Natural Science Foundation of China(Grant nos.:11672138,11602113)and Foundation of National Key Lab.of Transient Physics (Grant no.:6142604180407,JCKYS2020606004).

In impact problems,the yield stress of the metal materials is material model is based on a cumulative damage law:

in which:

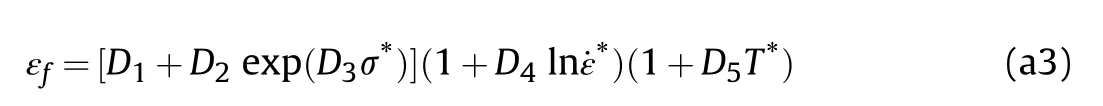
For Steinberg constitutive model,the shear modulus,G,before the material melts is de fined as

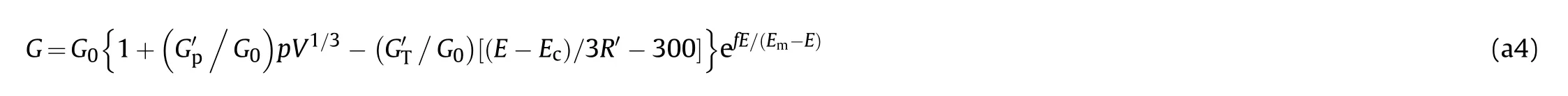
mainly in fluenced by strain hardening,strain rate and the temperature evolution.Thus,the Johnson-Cook[14]and Steinberg[9]constitutive models which are widely adopted in explosion and impact dynamic problems were used in the present study.The flow stressσin Johnson-Cook constitutive model is given as

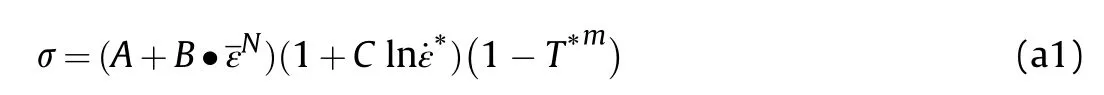
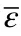
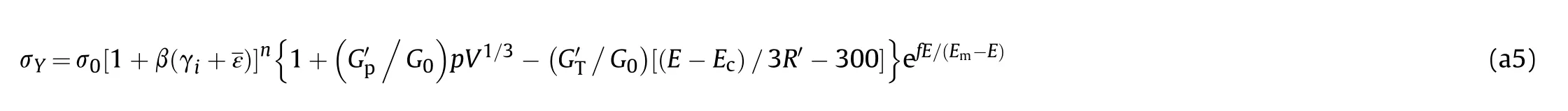
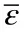
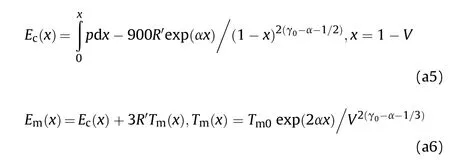
where Ris de fined by R=Rρ/A,R is the gas constant,ρis the density,and Ais the atomic weight;Tis the melting temperature,Tis the melting temperature at normal pressure,γis the Gruneisen constant,andαis a correction constant.Alter the material melt,G andσare set to one half their initial values.

In many dynamic experiments,measuring u(particle velocity)and u(shock velocity),it has been found that for most solids and many liquids over a wide range of pressure there is an empirical linear relationship between these two variables: