特定条件下高阶WENO 格式计算结果误差

刘君,韩芳,魏雁昕

大连理工大学 航天航空学院,大连 116024

计算流体力学(CFD)应用于工程项目时,和所有工业软件一样,希望它“又快又准”。回顾CFD 的发展历史,40年前需要花费几年时间才能完成的计算工作量现在仅需几分钟,CFD 依靠计算机技术在“快”方面取得了巨大进展。如果把增加网格量对提高计算结果精度的贡献去掉,相比日新月异的“快”而言,CFD 在“准”方面的发展可以用“停滞不前”来形容。尽管高精度格式作为研究热点已持续了20多年,目前商业软件广泛采用的还是20世纪80年代提出的二阶精度格式。

近年来,作者在对激波装配(Shock-fitting)法和激波捕捉(Shock-capture)法的对比研究中发现,对捕捉得到的计算结果,有时候使用高阶WENO 格式的计算误差明显比一阶迎风格式的计算误差大。针对这一现象,本文通过定性分析及算例测试等手段进行讨论,根据类型的不同,可分为以下4个问题。

1 间断问题

间断问题是超/高超声速可压缩流中不可避免的问题,本文对间断问题的讨论主要是因激波或接触间断运动而引起的非物理波动问题。

以笛卡尔直角坐标系下的二维守恒型Euler方程作为控制方程,在均匀正交网格上进行离散求解。通量分裂采用van Leer格式,空间离散采用一阶迎风格式及五阶WENO格式,包括WENO-JS、WENO-M、WENO-Z等。对应的,时间离散采用一阶显示格式或具有TVD 性质的三阶Runge-Kutta格式,时间推进步长按CFL=0.5计算。

1.1 激 波

计算区域设为[0,1]×[0,1],网格尺度Δ=Δ=0.01,选取初始位于=01处的正激波作为初始计算条件,激波运动马赫数为=30,波前波后参数为

选取无量纲时间=025时的计算结果进行讨论,此时激波运动至=085的位置。图1给出了流场密度、压力及熵沿=05的分布曲线,由于3种WENO 格式的分布曲线几乎一致,因此本文只给出了WENO-Z 格式的计算结果。从图中可以看出,在激波波后,存在一等熵一非等熵两个非物理波动,且与一阶迎风格式的结果相比,WENO-Z 格式捕捉到的波动宽度更窄,幅值更高。

图1 y=0.5线上不同格式的流场参数分布曲线Fig.1 Flow field parameter curves along line y=0.5

这种波动现象在文献[9]中已经提及,本文除了把不同精度格式的结果放在一起比较外,还给出了激波数值过渡区的内部特征结构。

在激波坐标系下,激波波前波后的参数应符合R-H 关系式,由式(1)所决定的激波质量通量、动量通量和能量通量分别为(,,)=(42,136,294)。图2给出了=05线上WENO-Z格式和一阶迎风格式所模拟激波守恒通量的分布曲线,从图中可以看出,尽管计算是以守恒型Euler方程作为控制方程,但在捕捉到的数值激波的过渡区内,其物理量的守恒特性不能保持,且与流场参数分布曲线相似,WENO-Z格式计算的守恒通量的局部最大误差要大于一阶迎风格式的计算结果。

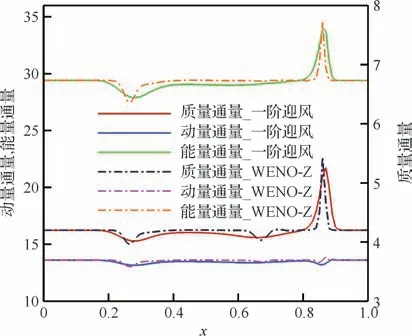
图2 y=0.5线上不同格式的守恒通量分布曲线Fig.2 Conserved flux curves in different schemes along line y=0.5

提取流场内沿方向流动参数,对相邻网格点进行Reimann分解,图3 是WENO-Z 格式捕捉到的激波过渡区在=02和=025两个时刻的内部结构分布。操作中发现即使相邻点有非常微小的变化也会分解出Reimann结构,因此设置压差Δ=001作为阈值,小于该值认为是光滑流场区域,用线段“”表示。

图3 不同时刻激波过渡区内的Reimann结构分布Fig.3 Distribution of Reimann structures within excitation transition zone at different time points

从图3可以看出,在激波的数值过渡区内主要存在两种Reimann分解结构,图中“”线段表示得到的是“激波-激波”结构,“”线段表示得到的是“稀疏波-激波”结构,而在不同时刻,激波过渡区内的Reimann分解结构分布并不相同。此外,作者还考察了不同格式和不同运动马赫数的激波过渡区,发现在过渡区内两种结构之间的变化复杂,其分布不具有规律性。

保持计算网格不变,将以上正激波旋转一定角度,激波与轴的夹角记为,初始激波放置在网格对角线下游以保证超声速出口边界不影响内部流场,如图4所示。文献[9]给出了不同旋转角度下激波运动所产生的密度误差云图和涡量云图,认为在网格点与初始激波不匹配的条件下,高精度格式的高分辨率特性很容易诱导出类似“湍流”的虚假结构。图5给出了=43.5°时一阶迎风格式及五阶WENO-Z格式所计算的流场涡量云图。图6是=01时刻,从(0.4,0)点出发与初始激波平行的直线上的涡量值分布曲线。由图5的涡量分布云图及图6的涡量值分布曲线可以看出,WENO-Z格式得到的激波波后流场结构分布更复杂,流场参数误差的最大幅值也更大。

图4 计算模型示意图Fig.4 Schematic diagram of calculation model

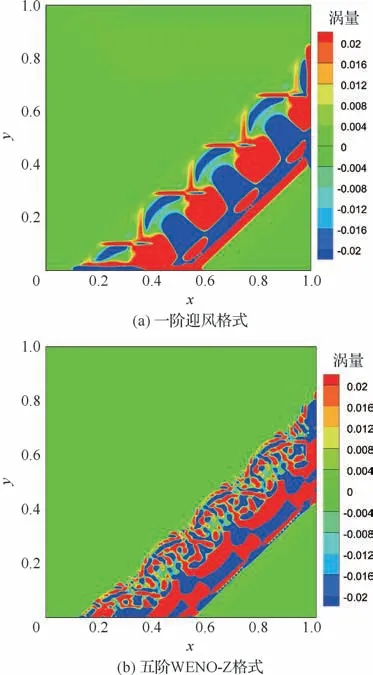
图5 不同精度格式得到的涡量云图分布Fig.5 Vorticity contours obtained by different precision formats

图6 不同精度格式得到的涡量分布曲线Fig.6 Vorticity distribution curves obtained by different precision formats

在文献[9]中,作者通过理论分析及数值实验得出以下结论：激波在计算过程中由数学间断发展成数值过渡区的过程中必然会出现以上非物理现象。结合本文结果可进一步发现,高精度格式的高分辨率特性会放大这种非物理的虚假波动,导致波后流场局部出现比一阶迎风格式结果更大的数值误差。

1.2 接触间断

接触间断算例的计算区域及初始条件如图7所示,网格尺度Δ=Δ=0.01。在此算例中,流场全场压力相等、速度相等,因此涡量=05×(v -u )的理论值为0。由于流场的压力及涡量分布在接触间断上下两侧非常相似,因此分别取接触间断上侧WENO-Z格式的结果和下侧一阶迎风格式的结果进行定性比较,如图8所示。由于WENO-Z格式的结果存在周期波动,图中取一阶迎风格式满足收敛条件2倍时间的计算结果进行比较。同时为了考察流场参数的波动特性,在流场下游设置了3个观测点(,)=(1.5,-0.5),(1.5,0),(1.5,0.5),观测点上压力随时间的变化曲线如图9所示。

图7 二维接触间断：计算区域和初始条件Fig.7 2D contact discontinuity flow：computational domain and initial conditions

图8 不同精度格式的压力和涡量云图Fig.8 Pressure and vorticity contours obtained by different precision formats

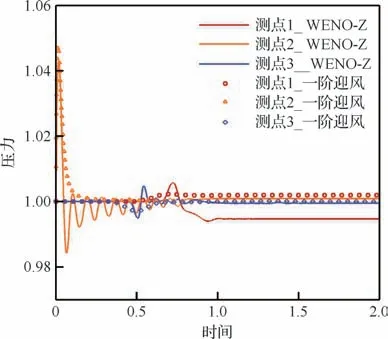
图9 接触间断测点处不同格式压力值随时间变化曲线Fig.9 Pressure change curves with time in different schemes at measurement points

在超声速流场求解过程中,接触间断从初始数学上的间断变成有厚度的数值剪切层,必然会诱导出旋涡、激波、膨胀波及其相互干扰的非物理结构。从本文算例看,不同精度格式的数值误差量级接近,但是,高精度格式出现了和物理流动非常相似的剪切层失稳现象。目前高精度格式常用来模拟转捩、DNS等非定常问题,如何从数值解中剔除这种虚假波动值得关注。

2 坐标变换问题

从笛卡尔直角坐标系(,)变换到柱坐标系(,)的变换函数可写成如下形式：

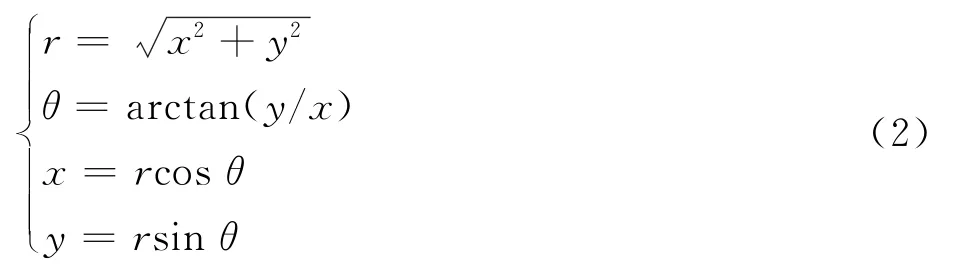
为了避免圆心处的奇性,取半径∈[1,2]的圆环作为计算区域,网格沿径向和周向均匀分布,这是贴体坐标系中严格正交、充分光滑的理想网格。采用与间断问题相同的计算格式数值模拟马赫数=3的均匀流,无量纲流动参数为

在文献[10]的计算中,作者发现在＞0 区域内环进口边界的处理算法会影响流场参数误差的分布特性,因此,本文直接选择＜0的区域计算,计算网格如图10所示。图11(a)是由一阶迎风格式计算得到的流场压力云图分布,图11(b)是由五阶WENO-Z格式计算得到的流场压力云图分布。图12是两种精度格式所得压力沿=15的周向分布曲线,其中横坐标为角度,以逆时针旋转为正。

图10 均匀流场计算网格Fig.10 Computational grid for uniform flow

图11 流场压力云图Fig.11 Contour of flow field pressure

图12 不同格式得到的沿r=1.5的周向压力分布曲线Fig.12 Pressure distribution curves along line r=1.5 for different schemes

在贴体变标系下应用WENO 格式计算均匀流场出现诱导误差的现象很早就被注意到,CFD工作者们对其消除方法进行了研究,本文通过定量比较,为“高精度格式的几何诱导误差更大”这一论点提供了论据。下面根据WENO 格式构造过程对压力沿周向变化这个新现象进行定性解释。

尽管计算空间网格总是均匀的,但是构造模板函数时不能直接采用直角坐标系下的原始变量(,,,)和守恒变量=(,,,),因 为这些量没有体现坐标变换过程中网格距离和网格面积等几何参数的变化。以二阶精度中心格式为例简单说明,在非均匀网格Δ≠Δ条件下,速度导数的离散形式为

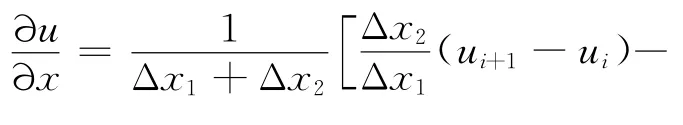
如果直接套用均匀网格的形式：

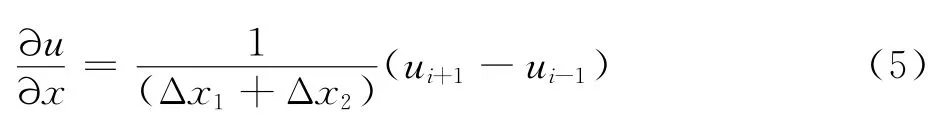
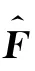
近年来国内外研究几何守恒律的学者认为,在有限差分法中坐标变换诱导误差出现的原因是采用软件生成的网格不能保证其正交性和光滑性,坐标变换系数的算法精度不能匹配有限差分格式的高精度,上述算例不支持这种观点。本文作者对其产生机理进行理论分析并且提出新的消除算法。

3 边界条件问题

CFD 在数学领域又称为偏微分方程的初边值问题,其中对于定常问题,初值仅影响收敛过程,由边界条件决定流场特性,因此理论上应该是将边界条件作为约束代入到流体控制方程建立边界方程。但是,由于边界方程与内部方程形式不同,再加上基于内点构造的差分格式很难直接用于边界点计算,因此,在实际应用中常采用简化模型。例如,无黏流动在固壁处满足不穿透条件,很少按照早期严谨的做法,把V =0代入Euler方程的特征线形式推导出边界方程后离散求解,目前常规的处理是在假设∂/∂=0的基础上,将其他物面参数根据等熵假设或者直接再进一步补充条件∂/∂=0和∂V/∂=0,然后离散以上空间导数,形成边界点和内点的关系式,在时间推进过程中根据内点信息预测更新边界值。

边界问题的算例计算模型如图13所示,模拟全部区域是激波对称相交流动,仅模拟上半部分就是激波在固体壁面的正规反射。按激波在固体壁面做正规反射求解时,由于固体壁面是平面,流场上下对称,可以通过在固体内部设置虚拟网格点直接求解边界值,计算得到的壁面参数和全流场中间对称流线上的流场参数完全相等。对于存在曲率的固体壁面,对称原理明显不成立,物体内部虚拟点如何取值是个问题,因此这种“镜像法”不具有普适性。在物体内部没有网格点的情况下,面临如何离散∂/∂=0等空间导数的问题,应用中发现单边高阶格式离散容易引起稳定性问题,因此,很多时候尽管内部网格点采用高精度格式,边界网格点也是采用一阶外推得到。但是在图13所示算例中,在中心对称流线处∂/∂=0成立,可以用来评价固体壁面的边界算法。

图13 激波正规反射计算模型示意图Fig.13 Sketch map for shock regular reflection

在全流场计算中,中间对称流线的压力记为,上下相邻网格线上的流场压力分别记为和,压力差Δ=-是数值模拟计算结果。如果模拟固体壁面正规反射,一阶外推得到边界值表示为：=,这种简化处理等效于在边界处引入Δ误差。

取图13虚线框内区域为计算区域,使用笛卡尔直角坐标系下的均匀正交网格,网格初始尺度为Δ=Δ=0.01。同时,为考察网格尺度对计算结果的影响,对网格进行2次加密,加密方式为一次加密即将初始网格或上一次加密网格的一个单元均分为4个网格单元,将初始网格及2次加密网格分别记为网格1、网格2、网格3。一阶迎风格式和WENO-JS 格式的Δ误差分布曲线见图14,可以看出WENO-JS格式得到的误差曲线幅值更大。图15给出了网格3上Δ=-的分布曲线,发现一阶迎风格式得到的结果为0,WENO-JS格式得到的曲线显示流场参数在中心对称线上下有明显的不对称现象。

图14 不同格式得到的边界误差分布Fig.14 Boundary error distributions for different schemes

图15 不同格式中心对称线上下压力差分布曲线Fig.15 Pressure difference distributions curves for different schemes above and below center line

采用以上设计模型,通过全流场Δ评估格式在边界降阶算法的误差,结论没有普适性,但至少表明高精度格式存在放大边界处算法误差的风险。

4 构造高精度格式的逻辑问题

从2013 年开始,NASA 联合航空航天领域众多高校、研究机构和企业的知名专家,面向美国已经开展及正在规划的重大工程项目需求,历时两年形成了一份预测未来CFD 软件发展前景的咨询报告。报告认为CFD 技术的发展目前已进入瓶颈阶段,并列举了CFD 要得到进一步发展需要攻克的六大关键技术,其中在“数值算法(Numerical Algorithms)”一项中提到了应用高精度格式遇到的问题。在以上具体算例的基础上,本文作者提出如下问题与同行交流讨论。

4.1 守恒型方程

通过前面的算例和定性分析可以发现,从守恒型方程出发的捕捉法,得到的激波数值过渡区内必然会出现质量通量、动量通量和能量通量不守恒的现象。既然“守恒”方程捕捉到的激波过渡区并不守恒,是否可以突破守恒方程的限制,采用新的方法数值模拟激波呢?

受肖锋等构造THINC 格式时用双曲正切函数描述流场接触间断的启发,根据激波前后参数在5个网格点之间拟合人工过渡区作为激波初始条件,显然内部3点不满足守恒性,但图16所示的计算结果表明,以人工过渡区作为初始条件的正激波在运动中不会产生1.1节中的非物理波动,采用函数模型来模拟激波也是可行的。

图16 不同初始条件下的正激波密度曲线(t=0.25)Fig.16 Density curves under different initial conditions for positive shock waves(t=0.25)

4.2 通量分裂格式

根据前面的数值模拟结果,如果掌握了激波过渡区内参数分布的规律性,就可以构建出没有虚假波动的初始激波模型。由于理论建模较为困难,首先采用精确Riemann解对数值过渡区内部波系结构进行分析,包括不同的通量分裂格式和差分格式,至今未发现激波过渡区内波系结构随激波参数的变化规律。

通量分裂格式既不能避免间断非物理,又不能准确反映双曲型方程守恒量沿特征线传播的空间特性,那么研究高精度格式是否固守这个技术途径值得探讨。

4.3 多点格式时空特性

考虑一维Euler方程,扰动的传播如图17所示。对一初始为静止的流场,在+2点处给予一扰动,扰动以声速传播。对于本文所用的显式格式,在满足稳定性要求的Δ时间内,向上游传播的影响范围不会超过+1点,因此,不可能影响到过点的流场参数。其次,即使不考虑时间因素,+2点的扰动能影响到点的流场,但是扰动经过+1点时要发生波的相互干扰,根据1.1节的Riemann分解结果,流场结构复杂,相互干扰效应不是高精度格式的有限模板及其固定系数能够描述的。

图17 扰动传播示意图Fig.17 Schematic diagram of disturbance propagation

文献[19]采用大的时间步长来关联空间多点的研究思路值得进一步探索。

4.4 特征线和依赖域

图18表示的是一个脉冲小扰动在超声速均匀流场中的传播,随着速度向下游传播过程中影响范围以声速的倍数逐渐扩大,流体微团到达点时至少点以上的区域已经感受不到曾经的扰动了。如果是持续扰动,在达到定常以后,点物理量的变化沿特征线保持,换言之,马赫锥内流场不再感受其扰动。由此看来,扰动的影响域在定常和非定常两种条件下是有差异的。同样,对于依赖域也存在类似的问题。图19是在超声速流场设计中得到广泛应用的二维特征线法,对于定常二维超声速等熵流动,只要知道2条特征线和流线的上游参数就可以确定点的流场,如果整个依赖域内还有其他点对其有影响,则变成了超定问题,与理论存在矛盾。此外,在构造点处的高阶格式时,必然会用到点在方向的相邻多点作为构造模板,但根据图19 可以看出,这些点对点处的流场并无影响。

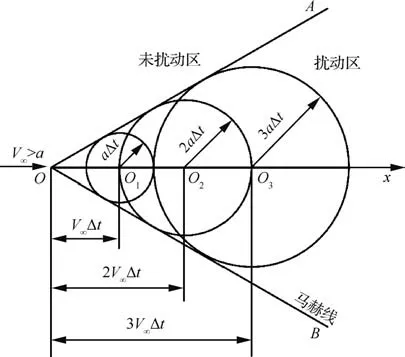
图18 小扰动在超声速流场中的传播[20]Fig.18 Propagation of weak perturbation in supersonic flow fields[20]

图19 定常二维超声速流场中的特征线与流线[21]Fig.19 Characteristic lines and streamlines in constant two-dimensional supersonic flows[21]

由此看来,目前采用多点拟合方法构建高精度格式的思路和双曲型方程描述波的传播过程在理论上存在矛盾之处。

5 结 论

有限差分的高阶WENO 格式因其强大的捕捉能力及辨识能力,使其能够捕捉到流场中的细微结构,对提高CFD 对流场的数值模拟精度具有重大意义。但以上算例表明,在某些特定情况下,高阶WENO 格式存在放大流场计算结果误差的风险,在使用时需要特别注意。通过对以上算例结果的讨论和分析,得到如下结论：

1)通过对数值激波附近守恒通量的比较,可以看出高阶WENO 格式得到的通量数值误差大于一阶迎风格式,且高阶格式捕捉到的流场参数在激波和接触间断处更容易出现非物理振荡。

2)如果没有配套的几何守恒律,在同一曲线网格下,高阶WENO 格式得到的几何诱导误差大于低阶格式。

3)高阶WENO 格式存在放大边界处算法误差的风险。

4)高阶WENO 格式采用多点模板的思路本质上不符合双曲型方程的特性。

综上,或许正如文献[22]所说：也许到了突破守恒方程、通量分裂、多点格式这些传统理论的时候了。