篦齿容积效应对盘腔空气系统瞬态特性的影响

王磊,毛军逵,2,*,王龙飞,潘进,邱长波,叶大海,蔡可信

1.南京航空航天大学 能源与动力学院,南京 210016

2.江苏省航空动力系统重点实验室,南京 210016

3.中国航发湖南动力机械研究所,株洲 412002

空气系统是航空发动机中重要的功能系统,其工作状况直接影响发动机的安全、可靠和高性能运转。通常,对于现代涡扇发动机,空气系统引气流量提升1%,则涡轮进口前温度需提升11 K以维持相同的推力水平,因此迫切需要对空气系统开展深入研究。

早期的空气系统设计分析以稳态/准稳态计算为主,许多学者对空气系统元件和网络的稳态特性进行了理论和试验研究,空气系统稳态/准稳态计算方法已经相当成熟。然而,实际的发动机工况并不能全部按照稳态/准稳态处理。当航空发动机处于过渡工况(如起动、加速、停车、快速机动过程等),尤其在极端工况(如主轴断裂、空中停车等)下,空气系统内部会出现复杂的瞬态响应现象。当发动机过渡状态和极端工况下产生的边界扰动作用于空气系统时,在各腔室的容积效应和内部流动非定常性作用下,可能会诱发短时的危险瞬态载荷,进而威胁发动机的安全运行和使用寿命,因此空气系统瞬态响应问题逐渐成为现代航空发动机研制中的关注重点之一。

近年来不少学者对空气系统中流路元件的瞬态特性进行了研究。如Kim 等通过数值计算和实验的方法,研究了限流孔对系统管路中压力波的影响及动态特性,结果表明限流孔非稳态与稳态模型的压力计算结果非常接近,因此相比于长管道,限流孔的瞬态响应特性基本可以忽略。May等提出了一个初始方法来解释盘腔瞬态模拟中的旋转效应,后来还改进了初始方法,通过考虑旋转腔内涡流结构的更多细节来模拟预旋盘腔系统的瞬态性能。张美华等、毛莎莎等分别对旋转和转静盘腔的瞬态响应特性进行研究,计算结果表明,盘腔出口流场的迟滞时间与进口边界工况和盘腔的几何特征有关。上述研究主要关注元件中流场参数的瞬态响应,同时有学者提出对瞬态过程中容腔的换热进行研究分析。Okita对瞬态工况下高压涡轮盘转静腔的流动与换热进行了研究,采用三维流-固耦合分析方法,得到实际发动机加减速过程中涡轮盘壁面温度和腔内空气温度的时间响应曲线。杨丽红等研究了换热效应对于等温容腔放气过程的影响,丁水汀等针对非绝热单孔容腔瞬态响应过程进行了建模与试验研究,提出了一种考虑换热影响的瞬态分析方法,后来,又基于自由射流、冲击射流及外掠平板换热理论,提出了一种模拟非绝热单孔容腔瞬态充气过程换热的理论方法,给出了换热特性准则式。

还有一些学者将关注焦点拓展到空气系统网络计算中。Gallar等为研究空气系统的瞬变流动问题,将复杂的空气系统结构简化为一系列相互串联的管道元件和有限体积的腔室,建立了腔室、管道的瞬态响应模型,获得了涡轮腔室压力、涡轮盘轴向力随时间变化曲线。朱鹏飞将管道和盘腔视作瞬态响应元件,提出了空气系统的瞬态网络算法,获得各类元件的截面流量关系式,进而建立瞬态网络节点压力残量方程,通过迭代求解,最终计算得到不同时刻的空气系统流量分配、压力和温度分布。Nikolaidis等考虑了容积效应与旋流的耦合影响,建立了空气系统一维瞬态计算平台,对过渡状态和极端运行条件下的空气系统响应特性进行研究分析,结果表明在过渡状态,空气系统参数变化平稳,可以用准稳态计算模拟空气系统的响应,而在极端运行条件下,空气系统工况会出现极端变化,必须要考虑其瞬态效应。

上述空气系统瞬态计算研究中,主要考虑了腔室和管道的瞬态特性。同时还有一些学者的研究表明,篦齿元件也表现出一定的瞬态响应特性。纪国剑采用数值模拟方法对直通式篦齿的起动特性进行了初步探究,研究结果表明发动机地面起动的60 s过程中篦齿泄漏系数逐渐减小,另外根据流场演化结果,经过1 s左右篦齿内部流场基本成型。朱鹏飞指出篦齿特性参数的时间响应曲线既表现出管道的振荡特征,也呈现出腔室响应的特点,同时发现篦齿的响应时间与管道相当。胡剑平等通过展开多容腔耦合的瞬态响应试验研究,发现相比于旋转盘腔的单元件试验结果,多腔室元件组合试验中由于元件之间的相互作用使得流路下游盘腔的响应时间大大增加。因此,在含多级封严的空气系统瞬态计算分析中,忽略篦齿元件对流路参数瞬态响应可能会带来明显的误差。

考虑到现代航空发动机精细化的设计需要,为了进一步提高空气系统设计精度,本文以多级封严盘腔为研究对象,建立盘腔和篦齿的一维瞬态数学模型,开展篦齿容积效应对盘腔空气系统瞬态特性的影响分析研究。重点关注考虑篦齿容积效应后盘腔内的流体参数响应时间变化及腔内的温度超调现象,以期为航空发动机空气系统的瞬态分析设计提供进一步的支撑。

1 计算模型及工况设置

1.1 计算模型

图1为某发动机多级封严盘腔的流路结构简图,以该多级封严盘腔为例进行空气系统瞬态计算分析。冷却空气从节点1流入,通过封严篦齿1进入转静盘腔中,对涡轮盘进行冷却,通过封严篦齿2流出到节点4。其中节点1为已知总压、总温的进口节点,节点4为静压已知的出口节点,节点2、节点3为待求解参数的盘腔进出口节点。

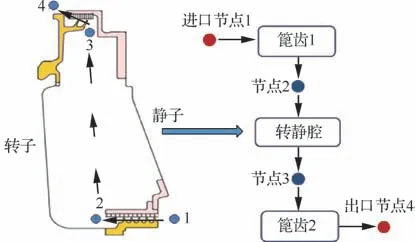
图1 多级封严盘腔流路示意图Fig.1 Schematic of multi-stage sealed disc cavity flow path

表1给出了上述多级封严盘腔的模型盘腔和篦齿元件的主要几何尺寸参数,其中篦齿1的齿数为5,篦齿2的齿数为2,篦齿1和篦齿2的几何特征尺寸参数一致。

表1 模型几何参数Table 1 Geometric parameters of model

1.2 工况设置

表2给出了上述多级封严盘腔的进出口瞬态边界条件。瞬态工况分为进口压力阶跃和进口压力斜坡2种典型工况,分别对应实际发动机的极端工况(如主轴断裂、空中停车等)与过渡工况(如起动、加速、停车、快速机动过程等)。并将忽略篦齿容积效应的计算算例命名为Cavity算例,将考虑篦齿容积效应影响的计算算例命名为Sealcavity算例。

表2 模型边界工况Table 2 Boundary conditions of model

阶跃工况下,进口压力突增至初始压力的1.1～1.3倍；斜坡工况下,进口压力在斜坡时间=0.15 s 内随时间线性递增至初始压力的1.1～1.3倍。图2展示了扰动幅值为1.2时,斜坡工况和阶跃工况下进口压力的变化。

图2 瞬态工况下的进口压力Fig.2 Inlet pressure under transient conditions

2 研究方法

2.1 一维瞬态模型

元件的瞬态特性分析是瞬态空气系统网络计算的基础,根据不同类型元件的瞬态响应特性,空气系统的通流元件可以大致分为2类：损失元件和响应元件。损失元件指限流孔、喷嘴等元件,由于其瞬态响应时间尺度极小,瞬态特性可以忽略。而本文主要的研究对象是具有明显容积效应的响应元件：盘腔和篦齿。

2.1.1 旋转盘腔

盘腔的实际结构和类型复杂多样,进气和出气方式也变化多样。为不失一般性,将图1中盘腔结构简化为文献[11]的典型转静盘腔(图3),并采用文献[11]中的数据来校验本文建立的瞬态元件模型。

图3 转静腔示意图Fig.3 Schematic of a rotor-stator chamber

对于腔室元件模型,其进出口流量与压力的关系公式为

式中：为半径位置处流体静压；为腔室进口静压；为入口半径；K为切向速度系数,大小与出口切向速度有关；为旋涡指数,当腔内为强迫涡时,=1,为自由涡时,=-1。

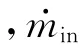
对于容积不变的腔体,忽略参数变量的空间不均匀分布,仅考虑腔内的质量平均参数,可以由质量守恒公式和理想气体状态方程推导得到腔内平均压力变化率

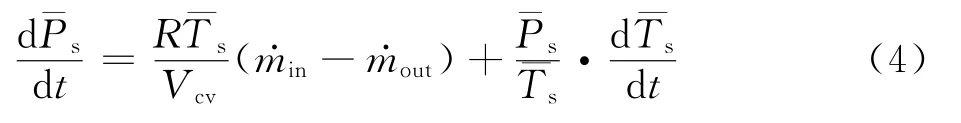
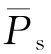
由能量守恒方程推导得出腔内平均温度变化率为

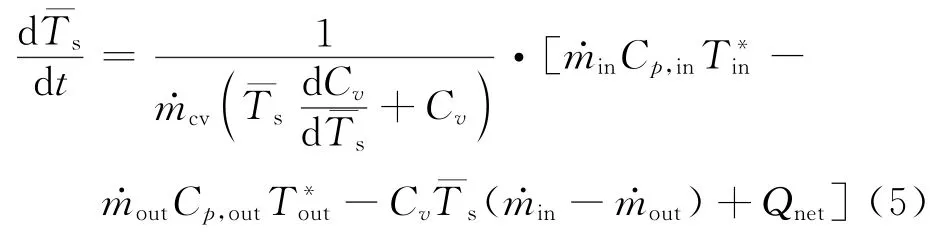
流体与轮盘对流换热量：

式中：为换热表面面积；为轮盘表面平均温度；为流体平均温度；为轮盘表面的对流换热系数。

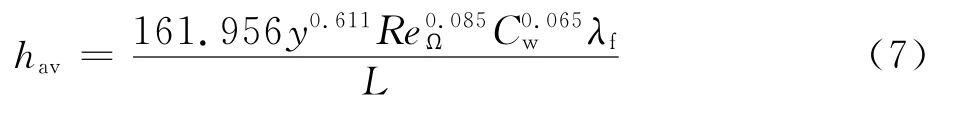
静止盘的表面换热可近似为自然对流换热,其计算公式为

式中：为流体普朗特数；为流体的瑞利数。

在瞬态计算中,腔内流量的改变会影响式(7)中流量系数的值,从而会导致换热系数变化,流体平均温度也会随之改变,因此对流换热量在瞬态计算中会随时间响应变化。

风阻温升热量计算公式为

式中：为轮盘力矩,计算公式为

式中：为力矩系数因子,对于一个确定的物理系 统,为 常 数；为 冷 气 密 度；为 当 地 半 径；ω为半径处冷气相对于轮盘的角速度,由式(11)计算得到,大小与盘腔进口切向速度系数K、当地半径有关；为圆盘力矩系数,对于转静系盘腔,其力矩系数由式(12)计算得到。

在瞬态计算中,盘腔进口流量的变化会导致流量系数的改变,从而影响式(12)中的值,式(9)中轮盘力矩也会随之变化,因此风阻温升热量也是瞬态变化量。

将建立的盘腔一维瞬态数学模型与文献[11,22]中的计算结果进行对比,其中文献[11]的计算结果为二维CFD 仿真结果,文献[22]为一维瞬态计算结果。

工况设定与文献[11,22]中的设定相同,得到的腔内平均压力随时间响应的变化曲线如图4所示。

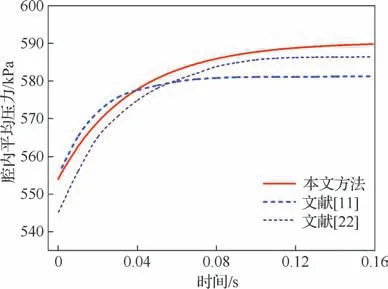
图4 腔内平均压力对比Fig.4 Comparison of cavity average pressure

从图4中结果可以看出,本文方法计算结果与文献[11,22]的结果基本一致,最大压力误差在1.7%以内。在时间达到0.08 s以后,文献[11]压力计算结果达到稳定,本文与文献[22]腔内平均压力仍在增大,这是由于文献[11]中忽略了对流换热的影响,因此流体参数计算收敛较快。而本文与文献[22]考虑了对流换热对流体温度的改变,所以在响应后期,本文计算结果与文献[22]更为接近,误差在1%以内,基本验证了本文模型的可靠性。

2.1.2 封严篦齿

在航空发动机空气系统的瞬态分析计算时,通常把篦齿视作可忽略瞬态特性的损失元件。而实际上,封严篦齿的齿腔内存在着一定的容积效应,其流场瞬态响应时间尺度在10s左右,因此在多级封严盘腔的多腔室之间瞬态耦合作用下,封严篦齿的容积效应也可能产生一定的影响。

为不失一般性,将图1中的篦齿结构简化为文献[21]中的典型直通式篦齿,建立篦齿的一维瞬态数学模型,并将该模型计算结果与文献[21]中的三维CFD 仿真结果进行对比,验证封严篦齿一维瞬态数学模型可靠性。封严篦齿的几何模型如图5 所示。表3 给出了篦齿模型的具体几何参数。

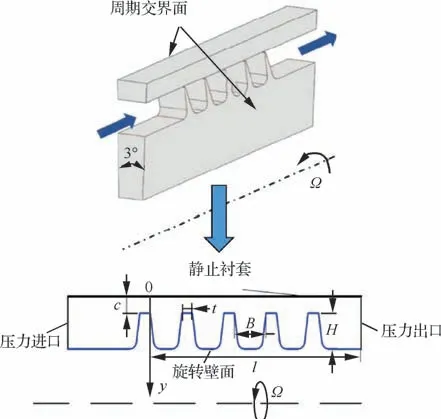
图5 封严篦齿示意图Fig.5 Schematic of a labyrinth seal

表3 封严篦齿几何参数Table 3 Geometric parameters of labyrinth seal

由于篦齿元件的几何特征参数过多,内部流动极为复杂,难以用单独的一维模型描述其瞬态特性,所以提出如图6所示的篦齿拆分模型。该拆分模型将齿尖缝隙处简化为瞬态效应忽略不计的压力损失元件,其压损与流量的关系在文献[4]中已经给出了详细的描述。而对于齿腔元件,将其视为具有容积效应的旋转腔室元件,当边界进口压力产生扰动时,篦齿内的齿腔元件在容积效应的作用下,会出现气体滞留现象,从而使得每个齿腔元件的进出口流量均不相等,每个齿腔内的流体的密度、压力、温度均会产生复杂的瞬态响应。其中齿腔元件的瞬态计算模型与2.1.1节中旋转盘腔的一维模型相同。

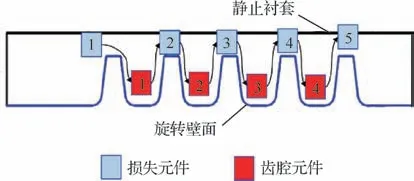
图6 篦齿拆分模型Fig.6 Model of labyrinth seal after split

对损失元件与腔室元件的串联网络系统进行一维瞬态计算(瞬态网络的计算方法在2.2节详细给出),并将此算例命名为验证算例2,算例中工况设定与文献[21]相同。

假定篦齿初始时置于100 kPa的均压环境中,无气体流动,在0时刻给予进口50 k Pa的压力阶跃,将一维瞬态模型计算结果与文献[21]中的三维计算流体动力学(CFD)仿真结果进行对比,最终结果如图7所示。

图7 齿腔内压力对比Fig.7 Comparison of tooth cavity pressure

从图7中可以看出,进口压力突增时,三维CFD 仿真结果中篦齿齿腔处会出现压力振荡上升现象。这是由于三维CFD 仿真计算中,进口与第一齿之间存在压力波的传播、反射,使得篦齿第一齿齿前压力存在明显波动,进而引起其他齿腔压力的波动。而一维瞬态模型计算并未考虑这一因素的影响,因此其结果显示各齿腔的平均压力随时间的响应变化是平滑上升的。但2种计算结果中压力响应快慢趋势一致,且最终稳定值也基本保持一致,表明一维瞬态模型中由于齿腔元件容积效应产生的流体参数迟滞现象与三维CFD 仿真基本一致。其中一维瞬态模型计算得到的出口齿腔处压力最大误差在2.2%以内,验证了封严篦齿一维瞬态模型的可靠性。

2.2 瞬态网络算法

在求解空气系统时,通常将复杂流路简化为由节点和元件组成的网络系统,通过求解网络系统的质量和动量守恒方程组来得到空气系统沿程参数分布。

图8展示了盘腔空气系统的流路简化示意图,、、为流路元件编号,其中元件为考虑容积效应的响应元件。

图8 盘腔空气系统流路简化示意Fig.8 Simplified diagram of flow path of disc cavity air system

对图8所示的空气系统流路建立守恒方程组求解计算,考虑容积效应的影响后,本文一维瞬态计算方法与传统的一维稳态流体网络计算的主要区别在于以下2点。

1)根据腔室元件的位置对流路进行划分

由于容积效应的影响,瞬态过程中元件之间的流量关系为

因此需要将腔室元件单独划分出来,将腔室上游的元件组合视为一条流路,腔室下游的元件组合视为另一条流路,从而建立起守恒方程组。

2)守恒方程的时间离散

在响应元件处建立守恒方程时,需要对3.1节中盘腔和篦齿的瞬态数学模型进行时间项离散,在每个时间步长内读入对应的边界工况,并对时间离散后的守恒方程组采用牛顿-拉夫逊法迭代求解,得到节点压力、流量、温度等参数,完成瞬态空气系统流体网络的求解,具体计算流程如图9所示。

图9 瞬态流体网络算法流程图Fig.9 Schematic diagram of transient fluid network algorithm

图9中,瞬态计算采用逐时间步长求解的计算方法,具体流程为：给定初始时刻的系统初场,将-Δ时刻的空气系统网络参数作为时刻的网络初场进行赋值,读入时刻边界节点参数,展开时刻的守恒方程组求解直至时刻节点压力()、流量()收敛,得到时刻空气系统网络参数,并作为+Δ时刻的网络初场,循环计算直至瞬态过程中收敛系数的绝对值小于设定值,本文取设定值大小为1×10。

收敛系数定义为

式中：()、(-Δ)分别为时刻和-Δ时刻的流场参数值；Δ为时间步长。当流场参数的收敛系数绝对值均小于设定值时认为系统参数达到稳定,响应过程结束。

3 结果分析

3.1 进口压力阶跃

当航空发动机紧急加速或刹车时,对空气系统进气参数造成的波动通常可以简化为阶跃函数,其中无量纲阶跃幅值是阶跃函数的一个重要参数,其大小反映了进口压力的扰动强度。图10(a)和图10(b)为进口压力阶跃工况下,阶跃幅值分别为1.1、1.2、1.3时,式(3)中转静盘腔内平均压力和平均温度随时间变化的响应曲线。

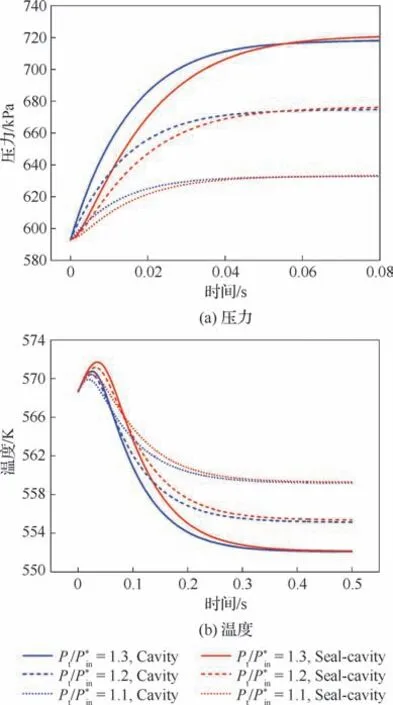
图10 阶跃工况下腔内流体参数随时间响应曲线Fig.10 Response curve of cavity flow parameters under inlet pressure step condition

图10中以施加压力阶跃工况为起始时刻的时间值。在不同阶跃幅值下,图10(a)中腔内平均压力随时间变化趋势为先逐渐增加,随后逐渐平缓至一稳定值,而图10(b)中腔内平均温度则在前0.05 s左右出现了明显的上升趋势,随后逐渐下降。腔内平均温度的响应速度明显低于腔内平均压力,腔内平均压力、温度分别在0.08 s和0.5 s内达到稳定,且Seal-cavity算例得到的腔内平均压力和腔内平均温度响应明显迟滞于Cavity算例。

为了定量分析腔内平均压力和腔内平均温度的响应快慢,定义瞬态响应过程中流动参数的响应残差达到并保持在5%以内的最短时间为响应时间,并将的大小作为瞬态过程响应速度的评价指标。

响应残差定义为

式中：c为流体参数在时刻的值；为初始稳态参数值；为响应达到稳定后的参数值。腔内平均压力与温度响应时间随阶跃幅值的变化如图11所示。从图11可以看出,随着阶跃幅值的增大,腔内平均压力的响应时间逐渐增大,而腔内平均温度的响应时间对阶跃幅值的变化并不敏感。

图11 腔内流体参数响应时间随阶跃幅值变化Fig.11 Variation of response time of cavity flow parameters with step amplitude

图11(b)中,Cavity算例的温度响应时间随阶跃幅值增大而减小,而Seal-cavity算例的温度响应时间随阶跃幅值增大而略有增加。这主要是因为腔内平均温度的响应时间受腔内平均温度的变化幅度及变化速率2个因素的共同影响。图10(b)所示的Cavity算例中,随着压力阶跃幅值的增大,虽然腔内平均温度的变化幅度增大,但腔内平均温度的变化速率也增大,因此腔内平均温度响应时间逐渐减小。而Seal-cavity算例中,由于篦齿容积效应的影响,相比于Cavity算例,随着压力阶跃幅值的增大,腔内平均温度变化幅度相对增大得更多,导致此时腔内平均温度响应时间略有增大。且考虑篦齿容积效应后,Seal-cavity算例腔内平均压力、腔内平均温度的响应时间明显高于Cavity算例的结果。当阶跃幅值为1.30时,与Cavity 算例的结果相比,Seal-cavity 算例的腔内平均压力响应时间相对提升了24.4%。腔内平均温度响应时间相对提升了9.3%。

为了研究篦齿容积效应对整个盘腔空气系统的影响,对上下游篦齿齿腔内的流体参数随时间响应变化进行具体分析。图12展示了压力扰动幅值为1.20时,上下游篦齿齿腔内平均压力、温度随时间响应的变化曲线。图12(a)、图12(b)为上游篦齿1的计算结果,其中按照流体流动方向将上游篦齿1中的4个齿腔依次命名为齿腔1～齿腔4,图12(c)、图12(d)为下游篦齿2的计算结果。

从图12(a)、图12(b)中可以看出,篦齿1中的4个齿腔的腔内平均压力和腔内平均温度的响应速度依次减小,这是由于元件之间的相互作用,在容积效应的叠加下使得下游齿腔内流体压力和温度的响应迟滞现象明显大于上游齿腔。由于篦齿2处于转静盘腔的下游,所以图12(c)、图12(d)中,篦齿2中齿腔的腔内平均压力和腔内平均温度响应时间远大于篦齿1。同样地,由于篦齿1元件位于转静盘腔的上游,所以考虑篦齿容积效应后,图11中Seal-cavity算例中盘腔内的流体参数响应时间大于Cavity算例的结果。

图12 篦齿齿腔内流体参数响应曲线Fig.12 Response curves of seal tooth cavity flow parameters

为了定量分析各元件流体参数响应时间同整个系统响应时间的关系,定义了无量纲响应时间系数用以评价元件响应时间对系统响应时间的影响大小,计算公式为

式中：t为元件内流体参数响应时间； 为元件进口边界处的流体参数响应时间,本文将元件紧邻的上游腔室类元件内流体参数响应时间视为 ；为系统响应时间,本文将转静盘腔内的流体参数响应时间视为。

表4给出了上下游篦齿和转静盘腔内的流体温度、压力响应时间系数对比,其中将篦齿1中出口齿腔的响应时间系数作为该元件的响应时间系数。从表4 中可以看出,流路中转静盘腔的压力、温度响应系数最大,对系统响应时间的影响也最大,上游篦齿1其次,下游篦齿2的响应时间系数最小。其中上下游篦齿内压力的响应时间系数远高于温度的响应时间系数,说明篦齿元件对系统内流体压力响应时间的影响更大。

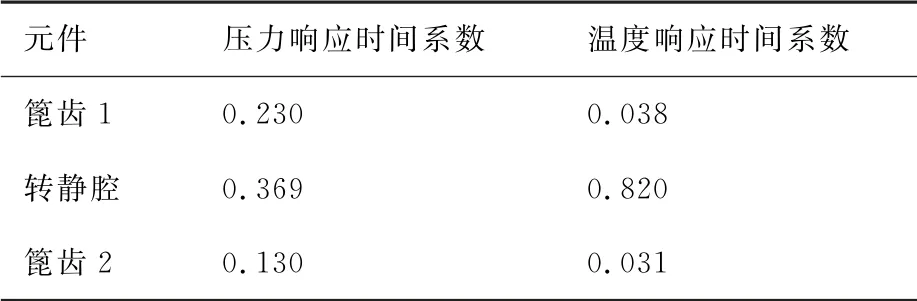
表4 元件中流体参数响应时间系数Table 4 Response time coefficient of flow parameters in each element

3.2 腔室容积的影响

Seal-cavity算例中腔内平均压力和腔内平均温度响应的迟滞是由篦齿齿腔内的容积效应造成的,而容积效应的作用程度主要取决于腔室容积的大小。由于实际航空发动机结构中盘腔容积的跨度很大,而篦齿齿腔容积的跨度相对较小,为了衡量航空发动机不同结构中篦齿容积效应的影响,通过改变盘腔容积大小,以无量纲参数盘腔-齿腔容积比进行定量分析,的计算公式为

图13(a)、图13(b)展示了压力阶跃幅值为1.2时,腔室轴向宽度分别为20、50、80 mm,对应为4.7、11.7、18.7时,转静盘腔内平均压力和平均温度随时间的响应曲线。

图13 不同盘腔-齿腔容积比下的腔内流体参数响应曲线Fig.13 Response curves of cavity flow parameters for differentγV

从图13中可以看出,的变化并不会影响腔内平均压力与腔内平均温度在响应到达稳定的值,但也随着盘腔轴向宽度的增大而增大,盘腔的容积效应使得腔内平均压力与腔内平均温度的响应迟滞现象愈加明显。图14(a)、图14(b)分别展示了上下游篦齿中压力与温度响应时间系数随的变化,其中篦齿1的响应时间系数为该元件出口齿腔的响应时间系数。

图14 腔内流体参数响应时间系数随盘腔-齿腔容积比变化Fig.14 Variation of t c of cavity flow parameters withγV

从图14可以看出,上游篦齿1中的压力、温度响应时间系数始终大于下游篦齿2。随着增大,上下游篦齿中压力与温度的响应时间系数减小,表明篦齿容积效应对系统流体参数响应时间的影响逐渐减小。当从4.7变化至18.7时,上游篦齿1中压力响应时间系数从0.55减小至0.17,相对减小了38%；温度响应时间系数从0.0726减小至0.0188,相对减小了75.2%。

3.3 进口压力斜坡

当航空发动机处于起飞、加速或减速等过渡工况时,空气系统进气参数的波动可以简化为斜坡函数。在进口压力斜坡工况下,由于盘腔压力的响应时间远小于斜坡时间0.15 s,所以进口压力斜坡工况的算例中腔内平均压力的瞬态特性可以忽略不计,后续仅对腔内平均温度的瞬态特性做具体分析。图15展示了扰动幅值为1.2时,进口压力阶跃和斜坡工况下,腔内温度随时间响应的对比。从图15 可以看出,相比于压力阶跃工况,压力斜坡工况下Seal-cavity算例的腔内平均温度响应曲线和Cavity算例响应曲线差异更大,说明压力斜坡工况下腔内平均温度的响应对篦齿容积效应更加敏感。

图15 阶跃、斜坡工况下腔内温度响应曲线Fig.15 Response curves of cavity temperature under inlet pressure step and ramp condition

图16展示了斜坡工况下腔内平均温度响应时间随扰动幅值的变化,可以看出随着扰动幅值的增加,腔内平均温度的响应时间逐渐增大。扰动幅值为1.3时,Seal-cavity算例的腔内平均温度响应时间为0.385 s,相比于Cavity算例提高了10.6%。

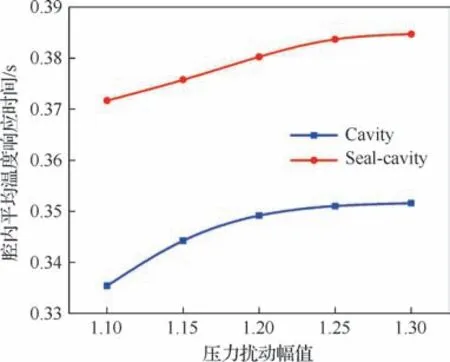
图16 进口压力斜坡工况下腔内温度响应时间Fig.16 Response time of cavity temperature under inlet pressure ramp condition

当进口压力增大,进入盘腔内的冷气流量增多,腔内气体温度应表现为逐渐下降的趋势,而上述结果中,不同边界工况下腔内平均温度的响应在瞬变前期表现出现明显的上升现象。将这种冷气流量增大情况下的腔内平均温度增加定义为温度超调现象。

图17、图18展示了Cavity算例中,盘腔进出口流量与盘表面平均换热系数在阶跃、斜坡工况下的响应曲线,用以分析腔内平均温度超调现象的产生原因。如图17所示,在瞬变初期,进口压力的突增导致盘腔进口流量突增,由于式(7)中的旋转盘表面平均换热系数会随着流量增大而增大,因此图18中在瞬变初期出现突增现象,对应的对流换热也会增强,从而导致温度会出现短时的上升趋势。随后换热系数趋于平稳,而由于图17中盘腔进口流量始终高于盘腔出口流量,式(5)中腔内滞留流量不断增加,因此腔内平均温度逐渐下降。

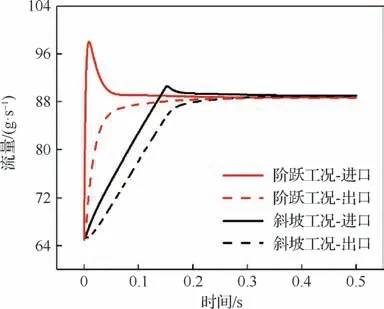
图17 阶跃、斜坡工况下盘腔流量响应曲线Fig.17 Response curves of mass flow rate under inlet pressure step and ramp condition

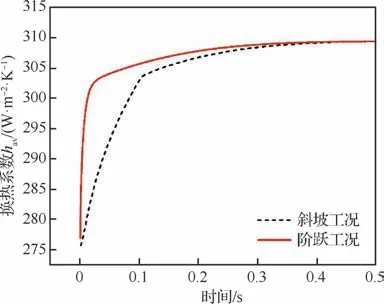
图18 阶跃、斜坡工况下轮盘表面换热系数响应曲线Fig.18 Response curves of h av under inlet pressure step and ramp condition

定义参数温度超调值用以定量分析腔内平均温度的超调现象,的计算公式为

式中：为响应过程中腔内平均温度所达到的最大值；为瞬态工况施加前的腔内稳态平均温度。进口压力阶跃和斜坡工况下的腔内平均温度超调值随扰动幅值的变化如图19 所示。从图19中可以看出,随着扰动幅值的增大,腔内平均温度超调值也随之增大,且阶跃工况下的明显高于斜坡工况下的。这是由于在响应初期,图17中阶跃工况下盘腔进口流量远高于斜坡工况,因此图18中阶跃工况下的轮盘表面平均换热系数更高,腔内的换热也更为剧烈,流体温升更高。

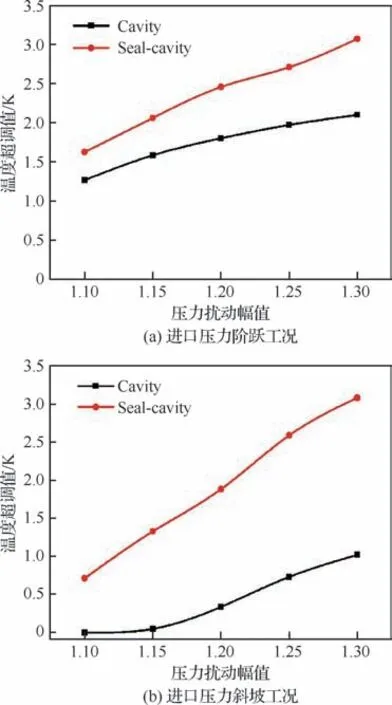
图19 进口压力阶跃、斜坡工况下温度超调值Fig.19 Overshoot of temperature under inlet pressure step and ramp condition

图19中Seal-caity算例的温度超调值明显高于Cavity算例,这是因为瞬态响应过程中篦齿齿腔内也会产生一定的温度超调现象,而由于流路中元件的相互作用,上游篦齿1的出口温度超调会使得转静盘腔进口温度升高,腔内温度也随之上升,从而使得Seal-cavity算例的温度超调值高于Cavity算例。图19(b)中,当扰动幅值为1.3时,Cavity算例的温度超调值为1.02 K,Sealcavity算例的温度超调值为3.2 K,相对提升了213.7%。

4 结 论

发展了考虑篦齿容积效应的一维瞬态数学模型,对某多级封严盘腔空气系统进行了计算,并与传统的一维瞬态计算结果进行了对比,得到如下结论：

1)对文献[21]中直通式篦齿模型进行了计算验证,提出的篦齿拆分模型的一维瞬态数学模型的计算结果与CFD 三维仿真结果误差较小,出口齿腔压力最大相对误差在2.2%以内,验证了本文一维瞬态数学模型的计算精度和可靠性。

2)由于元件之间的相互作用,上游篦齿元件的容积效应会使得流路中下游盘腔元件流体参数的响应时间增大。当阶跃幅值为1.30时,对比于Cavity算例的结果,Seal-cavity算例的腔内平均压力响应时间相对提升了24.4%,腔内平均温度响应时间相对提升了9.3%。

3)流路中转静盘腔的压力、温度响应时间系数最大,对系统响应时间的影响也最大,上游篦齿其次,下游篦齿的响应时间系数最小。随着盘腔-齿腔容积比增大,上下游篦齿对系统响应的影响减小,当从4.7变化至18.7时,上游篦齿1中压力响应时间系数从0.55减小至0.17,温度响应系数从0.072 6减小至0.018 8。

4)考虑篦齿的容积效应后,上游篦齿齿腔内的温度超调会影响下游盘腔元件的进口温度,从而使得腔内平均温度的超调值增大。当扰动幅值为1.3时,与Cavity算例的结果相比,Seal-cavity算例的腔内平均温度响应时间增大10.6%,温度超调值提升213.7%。