气相沉积法反应器内碳纳米管纤维运动模拟

刘宏霞 徐佳雯 陈廷

摘 要：為了研究碳纳米管纤维在气相沉积法反应器内的运动形态，并分析纤维运动形态对生成碳纳米管纤维的影响，首先采用数值模拟的方法对气相沉积法反应器内的气体流场进行数值求解，得到反应器内的气体流场的速度;然后在此气体流场中建立碳纳米管纤维模型并对其进行受力分析，得到纤维动力学方程，与气体流场控制方程组联立得纤维/气体两相流动模型;最后利用求解得到反应器内的气体速度，再对纤维动力学方程进行数值求解，从而得到碳纳米管纤维在反应器内的运动形态。模拟结果表明：气相沉积法反应器内的气体流场呈层流状态;由于气体从中心流入，纤维反应器中心轴线附近有较大波动，中心轴线附近气体流动区域逐渐扩大，加速度方向也产生改变，使得气体速度方向、大小均发生改变，纤维通过波动纠缠可以增加纤维束中纤维的连接，使之不易分散开来;而靠近壁面的气体流动逐渐稳定，导致靠近壁面的纤维运动形态逐渐平缓。通过模拟得到的纤维运动形态对形成碳纳米管纤维束有良好的促进作用。

关键词：气相沉积法;气体流场;纤维模型;数值模拟;纤维运动形态

中图分类号：TS101.2

文献标志码：A

文章编号：1009-265X（2022）02-0106-07

收稿日期：20210416 网络出版日期：20210708

基金项目：国家自然科学基金项目（51303121）;南通市基础科学研究项目（JC2019008）。

作者简介：刘宏霞（1994-），女，江西萍乡人，硕士研究生，主要从事数字化纺织技术、产业用纺织品方面的研究。

通信作者：陈廷，E-mail：tingchen@suda.edu.cn

Motion simulation of carbon nanotube fibers in a vapor deposition reactor

LIU Hongxia， XU Jiawen， CHEN Ting

（College of Textile and Clothing Engineering， Soochow University， Suzhou 215021， China）

Abstract： In order to study the motion morphology of carbon nanotube fibers in a vapor deposition reactor and the impact of motion morphology on the formation of carbon nanotube fibers， this paper first employs the method of numerical simulation to solve the gas flow field in the vapor deposition reactor numerically and then figures out the velocity of gas flow field in the reactor. After that， a carbon nanotube fiber model is built in this gas flow field and a force analysis is conducted to obtain a fiber dynamics equation. Combined with the gas flow field control equation set， we can get a fiber/gas two-phase flow model. Finally， the fiber dynamics equation is solved numerically， with the gas velocity in the reactor obtained through calculation， so as to get the motion morphology of carbon nanotube fibers in the reactor. The simulation results indicate that the gas flow field in the vapor deposition reactor presents a laminar flow state. Since the gas flows in from the center， there is a great fluctuation near the central axis of the fiber reactor. The gas flow area near the central axis gradually expands， and the direction of acceleration changes， making the direction and magnitude of gas velocity change accordingly. The undulating entanglement of fibers can increase the bond of fibers in the fiber bundle， making it difficult to spread out. The gas flow near the wall gradually becomes stable， making the fiber motion near the wall gradually flatten out. The motion morphology of fibers obtained through simulation has a good promoting effect on the formation of carbon nanotube fiber bundles.

Key words： chemical vapor deposition; gas flow field; fiber model; numerical simulation; motion morphology of fiber

碳纳米管纤维的开发开拓了纺织学术研究与商业应用的全新领域。气相沉积法可以实现碳纳米管纤维一步法制备，该工艺程序简单、纺丝速度快、成本较低[1]。碳纳米管纤维的运动形态与碳纳米管纤维的生成品质有着重大的联系，因此研究碳纳米管纤维在气相沉积法反应器内的运动是非常有必要的。

碳纳米管纤维在反应器中生成、运动符合流体力学中经典的两相流问题，随着计算机技术的发展，数值模拟方法成为研究纤维/气体两相流动问题的重要手段[2]，这极大地节省了实验时间，并且能够避免一些实验危险。许多研究者通过建立纤维/气体两相流动模型，经过数值模拟得到纤维在气流中的运动形态，进而研究纤维的成纱机理。近年来很多运用数值模拟方法研究高速气流的新型纺纱技术如喷气纺[3]、喷气涡流纺[4]等，也有运用数值模拟方法获得转杯纺纱通道内纤维运动规律[5]，而气相沉积法制备碳纳米管纤维反应器内部是高温、低速环境，且充满易燃气体，实验研究存在很大的局限性，缺乏有关于碳纳米管纤维在反应器内运动的研究。

纤维/气流两相流动的主要研究重点是纤维动力学方程的建立，纤维不同于其他刚性物体，它具有刚性和柔性的特征，因此对其受力分析时不能简单的只考虑刚性受力，在进行纤维运动模拟之前需要对纤维进行简化，建立纤维模型。根据以往的研究，纤维模型主要包括以下3类：第一类是球链模型[6]，后面又发展了珠-簧链模型[7]、针-链模型[8-9];第二类是珠-杆模型[10-11]，后面又延伸出珠-弹性杆[12];第三类是将纤维有限元划分，再研究整体的纤维运动[13-15]。

本文在建立气相沉积法反应器内气体流场数值模型的基础上，采用单向耦合方法建立碳纳米管纤维在气体流场中的动力学方程并进行求解，以此来探究纤维在反应器内的运动形态，为碳纳米管纤维的制备生成奠定了基础。

1 气相沉积法反应器内气体流场数值模拟

1.1 反应器几何模型

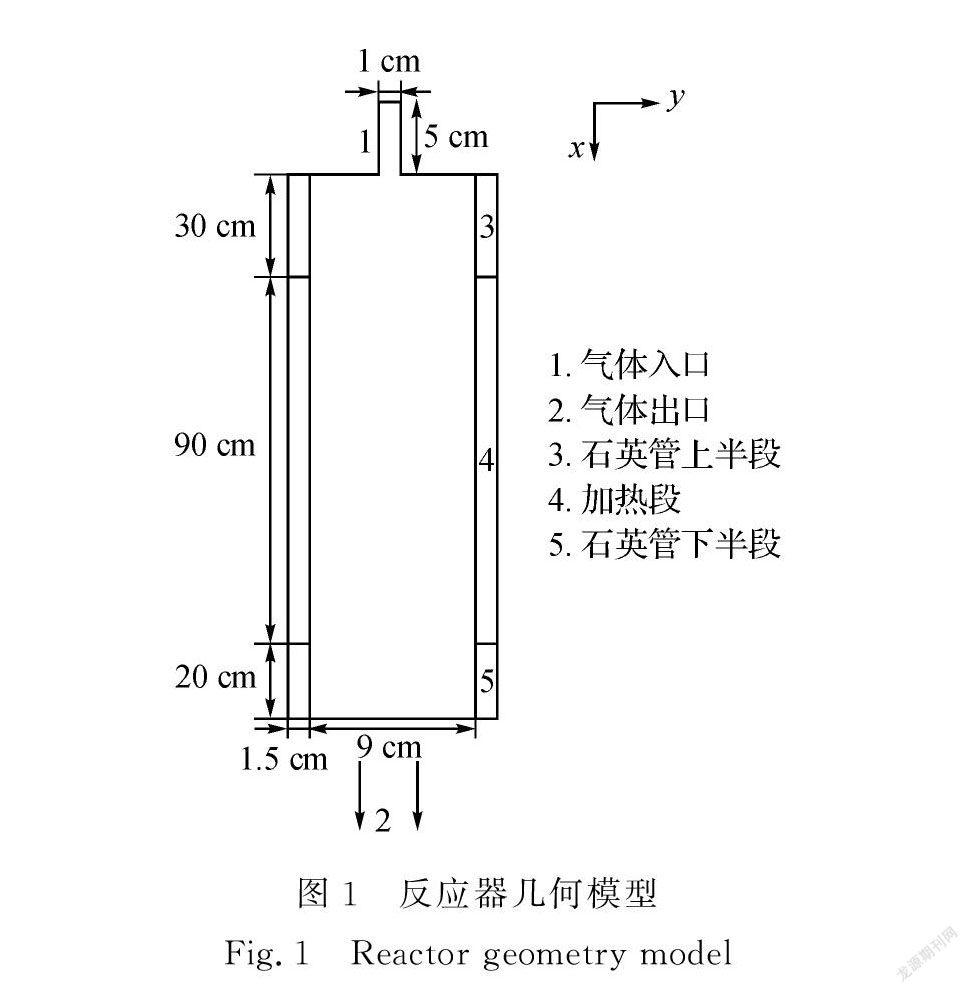
反应器由一个上下两节的圆柱体构成，上节圆柱体代表进气口，下节圆柱体代表反应器主体炉管。反应器只有一个进气口，并且是轴向对称结构，为了方便计算，可以只截取其径向剖面构建二维几何模型，并对反应器其他部件进行适当简化。载气从进气管（x轴方向）进入反应炉内，进气管长度为5cm，内径为1cm，随后进入内径为9cm、长度为140cm、壁面厚度为1.5cm的反应器主腔室，其中，加热段为90cm的铜电热体，提供约为1500K的反应温度，上下为30、20cm的石英炉管。几何模型如图1所示。

网格划分：采用结构化网格（即Map方法）划分，网格形式为四边形网格（Quad），网格间距（interval size）取0.00125，就可以得到54080个1.25mm×1.25mm的矩形小网格。

入口边界：速度入口，载气速度为1.2 m/s，方向与x轴平行，入口温度为600K。

出口边界：压力出口，为标准大气压，出口温度为室温。

壁面边界：流体区域介质为氢气，3、5区的介质为石英，4区的介质为铜。

1.2 求解控制参数

反应器入口的气体速度不大，根据雷诺数小于2300，选择层流模式，根据本文气体流动的工作状况选择压力-速度耦合求解，采用PISO算法处理，对于动量方程和能量方程的离散方法采用二阶迎风格式（Second order upwind）。

1.3 模拟结果

根据所建立的模型，对反应器内的气体流场进行计算，得到气体流场速度矢量图，如图2所示。从速度分布云图可以看到气流以1.2 m/s的速度进入反应器炉体之后，一直保持比较稳定的层流状态，进入主体炉管之后气体流动区域稍变大，气流的速度方向在反应器内部大都是向前并且速度大小無很大的变化，这也符合层流模型的规律，在近壁区可以观察到一些细微的回流区。

图3为不同y位置的气体速度分布曲线，气流在x轴坐标0～0.15 m的范围内有一个加速过程，这是由于气体受到与x轴方向平行的重力加速度，加速可达到2.25 m/s，之后受到流场的作用力，速度开始下降，最后趋于平衡且速度大于0。

2 碳纳米管纤维在反应器内的运动模拟

2.1 纤维模型的建立

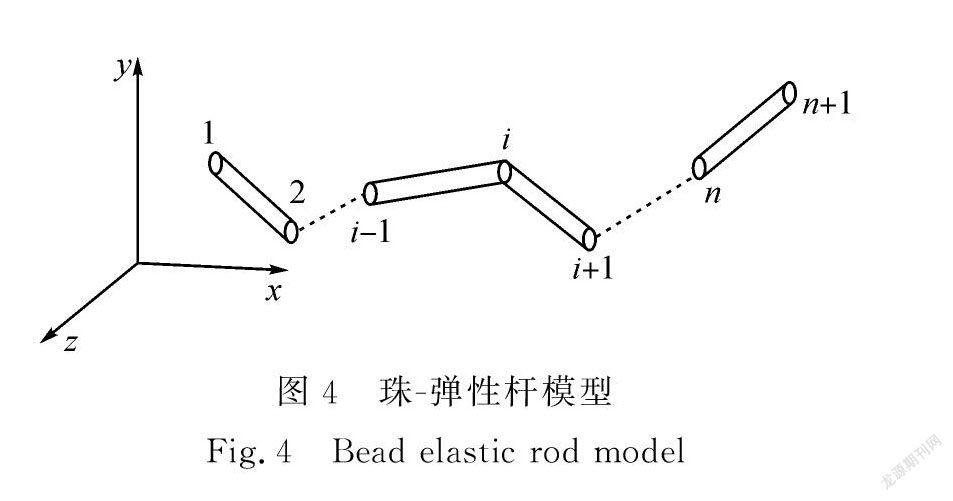
本文采用珠-弹性杆纤维模型，由n个球状珠子和n-1根与珠子同直径的弹性杆连接而成，如图4所示。当纤维在气流场中运动时，为了简化模型，假设纤维的质量和所受的合力全在珠子上，而纤维产生的拉伸弯曲变形在弹性杆上。纤维通过改变两珠的距离产生弹性伸长，这表现为珠子上所受的伸长回复力，沿纤维杆伸长的方向;改变弹性杆的弯曲挠度产生弯曲，珠上受到弯曲回复力，沿纤维杆的法向方向。

在纤维模型中，第i个珠子与珠i-1和珠i+1连接，则珠i的质量m i定义：

m i=ρ f2l i-1，i+l i，i+1（1）

式中：ρ f为纤维的线密度，l i-1，i，l i，i+1为纤维段（i-1，i）（i，i+1）的长度。对于第一颗和最后一颗珠子的质量，要根据镜面反射形成虚拟珠，即虚拟珠1和虚拟珠n，则m 1=ρ f2l 0.1+l 1，2，m n=ρ f2l n-1，n+l n，n+1。

2.2 纤维受力

2.2.1 伸长回复力

由于受到气流的牵伸，纤维产生伸长回复力，假设珠i-1和珠i受到伸长回复力，两珠的距离被拉伸，则珠i所受的伸长回复力为：

F ei=πd2E4lΔl（2）

式中：E为纤维的弹性模量，d为纤维直径，l为纤维长度， Δl为纤维的伸长，F ei的方向是沿纤维段的拉伸长度方向。

2.2.2 弯曲回复力

纤维被弯曲时，当如图5，纤维段（i，i+1）与（i，i-1）弯曲成θ i，珠i受到弯曲回复力F bi的作用：

F bi=2EI bl2 （i，i+1）·θ（3）

式中：E为纤维的弹性模量，I b为惯性矩，由于纤维是长柱体，因此采用圆形截面的惯性矩，如下：

I b=πd4 f64（4）

d f为纤维直径，θ i可以通过两珠的位置确定大小，即：

cosθ i=e i·e i+1（5）

e i和e i+1为珠杆（i-1，i），（i，i+1）的单位向量。

2.2.3 气流曳力

纤维在气流场中所受外力主要是流场施加的，这种外力主要表现为气流曳力F di。这种曳力又表现为两部分：一部分是由于纤维与流场交界的边界层的黏性剪切应力产生的，叫摩擦曳力F f i-1，i，方向沿着纤维表面的切向方向;另外一部分是由于流场沿y轴方向上的压力都不同而产生压力差，使得纤维的径向方向上产生压差而受到压差曳力F p i-1，i，方向沿纤维表面法向方向。在计算曳力时，每个珠受到的曳力是由该珠的前后两根连接杆所受的曳力矢量合成的，即

F di=12F d i-1，i+F d i，i+1（6）

式中：F d i-1，i和F d i，i-1分别为杆（i-1，i）和杆（i，i+1）所受的曳力。单独对纤维段（i-1，i）分析，杆所受的曳力等于摩擦曳力和压差曳力之和：

F d i-1，i=F f i-1，i+F p i，i+1（7）

式中：F f i-1，i，F p i，i+1分别为作用在纤维段（i-1，i）上的摩擦曳力和压差曳力。

具体曳力公式如下：

F f i-1，i=π2c fρdl i-1，iv2 rti（8）

F p i-1，i=π2c pρdl i-1，iv2 rni（9）

式中：v rti，v rni 分別为珠i处的相对速度沿纤维表面切向和法向的分量，气流与纤维的相对速度（V a i-V f i）; l i-1，i为纤维段的长度，ρ为气流场的密度。c f为切向曳力系数，c p为法向曳力系数。切向曳力系数与雷诺数有关，本文所处的工况雷诺数约为128，本文可以根据“标准阻力系数曲线”来确定法向曳力系数c p。

2.3 材料特性及初始条件

根据牛顿第二定律，珠i在气体流场中的动力学方程为：

m i=d2r idt2=F ei+F bi+F di（11）

式中：r i表示珠i在流场中的位置，通过求解珠i的动力学方程，可得到不同时刻珠子在流场中的位置，最后汇总可以得到纤维的运动形态。

本文是对气相沉积反应器内的纤维运动进行二维模拟，纤维直径d f=38μm，长度L f=37.5mm弹性模量E=500GPa。选取三个坐标点作为纤维运动的头端位置，纤维具有一定的初速度，假设该初速度等于反应器内该坐标的气流平均速度。纤维的总长度不发生变化，当 （r i-r i-1）=L f 时，停止计算。

3 结果与讨论

根据上述初始条件和气体流场模拟的结果来计算纤维动力学方程，选取（0.400，0.001）、（0.400，0.005）、（0.400，0.010）、（0.400，0.015）、（0.400，0.200）、（0.400，0.250）、（0.400，0.300）7个纤维头端位置，根据气体流场的模拟，得到这7个位置上y轴的速度曲线，气流在0～0.5 m 的范围内都有一个加速过程，然后速度逐渐降低直至达到稳定，这与徐子超等[16]模拟的碳纳米管纤维反应器内的气体流场速度分布一致，这是由于气体受到与其初速度同方向的重力作用，获得加速，后受到的流场曳力使气体速度下降至稳定。

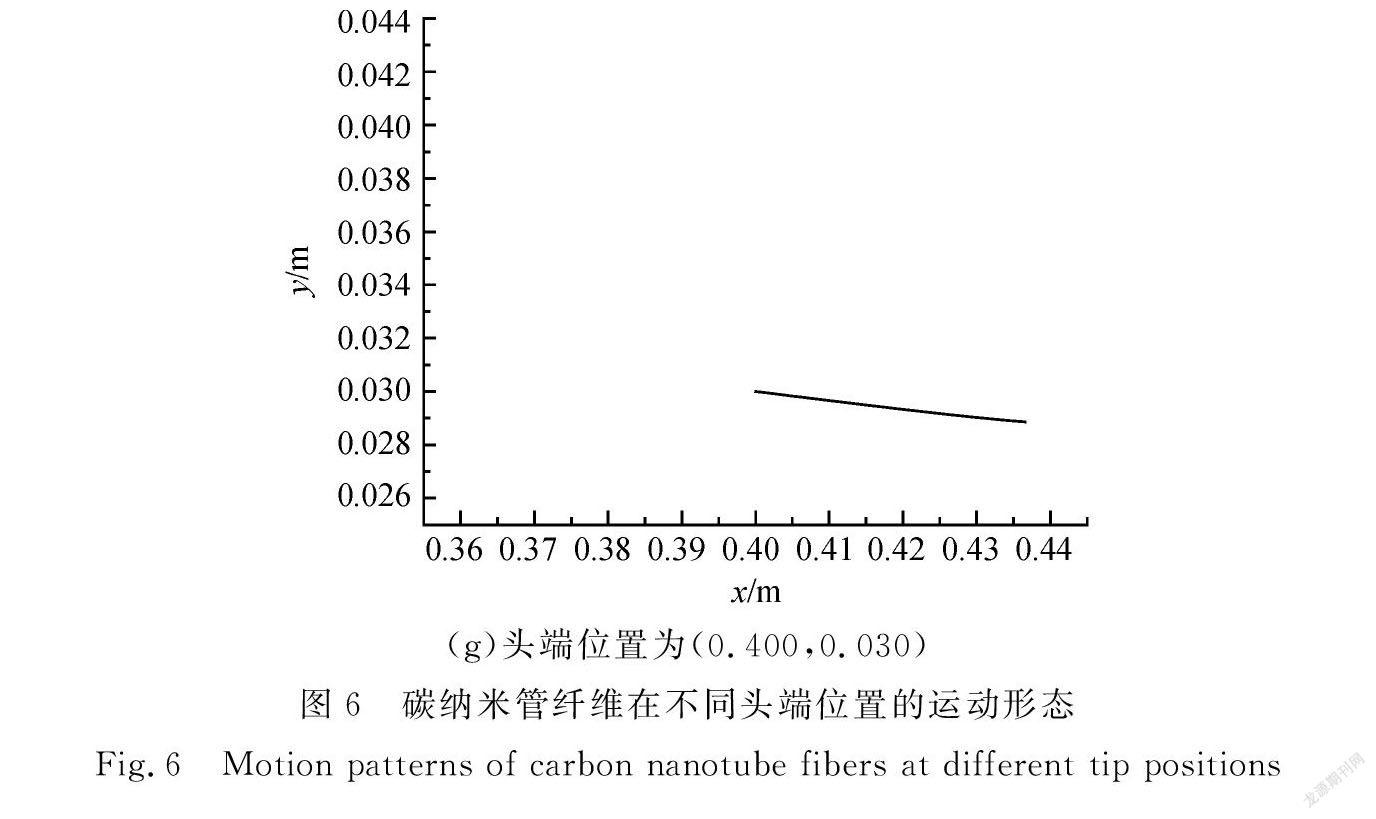
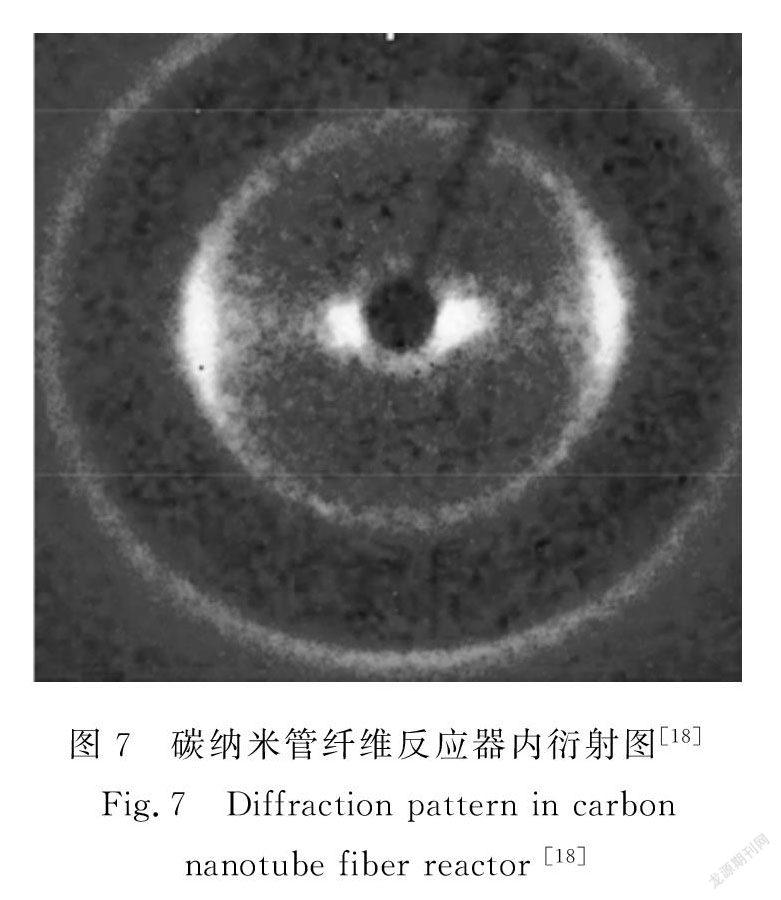
从头端位置释放纤维，运用MATLAB软件计算得到该位置纤维的运动形态，如图6所示。靠近中心轴线上（0.400，0.001）位置释放的纤维前端呈平缓状态，后端发生波动，根据速度曲线图，可以观察到靠近中心轴线上的气流速度起伏较大;而（0.400，0.005）位置与（0.400，0.010）位置的气流速度浮动变小，使纤维运动变平缓;（0.400，0.015）处于速度变化的交界处，从速度云图可以看到速度大小的颜色发生改变，导致纤维运动起伏变大。以上4个位置的减速过程的加速度很大，方向指向反应器前端，因此这些位置的纤维往反应器前端运动。从（0.400，0.200）到（0.400，0.300）的纤维运动形态都比较平缓，该区域的气流速度稳定，符合气体流场层流[17]状态，使得纤维运动方向逐渐与x轴平行，从反应器轴向观察得到纤维是较平直的，这与Fiona等[18]从反应器得到的碳纳米管纤维运动衍射照片中观察到碳纳米管纤维的纤维轴是垂直的现象是相符合的，如图7所示。

4 结 论

运用数值模拟的方法模拟了碳纳米管纤维在气相沉积法反应器内的运动形态，得到了以下结论。

a）对气相沉积法反应器内的气体进行模拟，得到气体速度矢量图，结果表明气体速度进入反应器炉管后，一直保持稳定的层流状态，速度大小沿轴线先有一段加速过程再不断减小直至稳定。

b）建立的珠-弹性杆纤维模型模拟反应器内纤维运动是可行的，纤维在反应器内中心轴线位置附近有波浪形运动，头端位置越靠上，由于气体速度保持稳定，纤维运动方向逐渐与气体流动方向一致。

c）通过对反应器内不同位置释放的纤维运动形态进行分析，总体上纤维的运动形态比较平顺，这验证了碳纳米管纤维束的形成机理。

参考文献：

[1]袁霞，刘艳秋，牛治群，等.化学气相沉积法合成纳米碳管阵列研究[J].化学与粘合，2009，31（2）：24-27.

YUAN Xia，LIU Yanqiu，NIU Zhiqun，et al.Synthesis of carbon nanotube arrays by chemical vapor deposition[J].Chemistry and Adhesion， 2009，31（2）： 24-27.

[2]曾泳春.纤维在喷嘴高速气流场中运动的研究和应用[D].上海：东华大学，2004.

ZENG Yongchun. Study on Fiber Motion in High Speed Airflow within the Nozzle and Its Application[D].Shanghai： Donghua University， 2004.

[3]吴重敏，陈革，薛文良.基于FLUENT的喷气织机主喷嘴内流场的三维数值模拟[J].东华大学学报（自然科学版），2010，36（1）：66-69.

WU Chongmin，CHEN Ge，XUE Wenliang.Three dimensional numerical simulation of flow field in main nozzle of Aair-jet loom based on FLUENT[J]. Journal of Donghua University （Natural Science），2010，36（1）：66-69.

[4]尚珊珊，余子开，郁崇文，等.喷气涡流纺旋转气流场及纱体运动的数值模拟[J].东华大学学报（自然科学版），2019，45（5）：665-675.

SHANG Shanshan，YU Zikai，YU Chongwen，et al.Numerical simulation of rotating air flow field and yarn motion in air jet bortex spinning[J]. Journal of Donghua University （Natural Science）， 2019，45 （5）： 665-675.

[5]林惠婷，汪军.纤维在输纤通道气流场中运动的模拟[J].纺织学报，2018，39（2）：55-61.

LIN Huiting，WAN Jun.Simulation of fiber movement in fiber conveying gas flow field[J]. Journal of Textile Research， 2018，39 （2）： 55-61.

[6]程悌吾.粘弹性纤维在均匀变形流场中的悬浮动力学[J].中国纺织大学学报，1988，14（6）：89-97.

CHEN Diwu.Suspension dynamics of viscoelastic fibers in uniform deformation flow field[J]. Journal of China Textile University， 1988，14 （6）： 89-97.

[7]YAMAMOTO S， MARSUOKA T A. Method for dynamic simulation of rigid and flexible fibers in a flow field[J].Journal of Chemical Physics，1993，98（1）：644-650.

[8]NYLAND G H， SKJETNE P， MIKKELSEN A， et al. Brownian dynamics simulation of needle chains[J]. Journal of Chemical Physics，1996，105（3）：1198-1207.

[9]MIKKELSEN A， KNUDSEN K D， ELGSAETER A. Brownian dynamics simulation of needle-spring chains[J].Physica A Statistical Mechanics and Its Applications，1998，253：66-76.

[10]GUO H F， AN X L， YU C W. Numerical study on the principle of yarn formation in murata air-jet spinning[J].Journal of Textile Engineering.2007，53（5）：173-178.

[11]曾泳春，郁崇文.氣流/纤维两相流动的数值计算和实验的研究[J].东华大学学报（自然科学版），2002，28（3）：109-113.

ZENG Yongchun，YU Chongwen.Numerical calculation and experimental study of gas / fiber two-phase flow[J]. Journal of Donghua University（Natural Science）， 2002，28 （3）： 109-113.

[12]张勇，曾泳春，王云侠，等.基于珠-杆模型的喷气涡流纺喷嘴气流场中的纤维运动规律[J].东华大学学报（自然科学版），2013，39（5）：583-589.

ZHANG Yong，ZENG Yongchun，WAN Yunxia，et al.Fiber motion law in air flow field of air jet vortex spinning nozzle based on bead rod model[J]. Journal of Donghua University （Natural Science）， 2013，39 （5）： 583-589.

[13]裴泽光，郁崇文.喷气涡流纺喷嘴中纤维运动的数值模拟[J].东华大学学报（自然科学版），2010，36（6）：615-621，644.

PEI Zeguang，YU Chongwen.Numerical simulation of fiber motion in jet vortex spinning nozzle[J]. Journal of Donghua University （Natural Science）， 2010，36 （6）： 615-621，644.

[14]李二明，華志宏，薛文良，等.纤维弹性细杆模型几何大变形静力学分析的有限元方法[J].东华大学学报（自然科学版），2016，42（6）：916-921.

LI Erming，HUA Zhihong，XUE Wenliang，et al.Finite element method for geometric large deformation static analysis of fiber elastic thin rod model[J]. Journal of Donghua University （Natural Science）， 2016，42 （6）： 916-921.

[15]郭臻，李新荣，卜兆宁，等.喷气涡流纺中纤维运动的三维数值模拟[J].纺织学报，2019，40（5）：131-135.

GUO Zhen，LI Xinrong，BU Zhaoning，et al.Three dimensional numerical simulation of fiber motion in air jet vortex spinning[J]. Journal of Textile Research， 2019，40 （5）： 131-135.

[16]徐子超，吴丽莉，陈廷.直接气相沉积法制备碳纳米管纤维的研究进展[J].纺织导报，2019（6）：67-71.

XU Zichao，WU Lili，CHEN Ting.Research progress of carbon nanotube fibers prepared by direct vapor deposition[J]. China Textile Leader， 2019 （6）： 67-71.

[17]袁亚雄.高温高压多相流体动力学理论与应用[M].北京：北京理工大学出版社，2016：347.

YUAN Yaxiong.Theory and Application of High Temperature and High Pressure Multiphase Hydrody-namics[M]. Beijing： Beijing Institute of Technology Press， 2016：347.

[18]FIONA S， ADAM B， ALAN W. Direct spinning of CNT fibers： Past， present and future scale up[J].Carbon，2019，152：218-232.