基于自适应模板匹配的四方连续花型最小单元提取
2022-03-29龙颖吕叶馨郭子翊黄振华邹奉元
龙颖 吕叶馨 郭子翊 黄振华 邹奉元











摘 要:为实现连缀式及重叠式四方连续花型最小单元的自动提取,对矩形模板边长占比进行迭代,探究了矩形模板大小对全局模板匹配的影响,再利用垂直矢量法分析了匹配所得矩形的中心点点集,揭示出像元重复规律与最小单元的对应关系;以相似度均值度量提取结果的准确性,阐明了最小单元重复次数与相似度均值的关系;通过分析模板匹配的适用性,提出了自适应阈值模板匹配的方法,改进后相似度均值平均可达94.29%。结果表明,该方法能有效实现连缀式及重叠式四方连续花型最小单元的提取。
关键词:最小单元提取;自适应模板匹配;四方连续花型;相似性匹配;直方图相似度
中图分类号:TS941.26
文献标志码:A
文章编号:1009-265X(2022)02-0191-06
收稿日期:20210311 网络出版日期:20210708
基金项目:浙江省教育厅项目(Y201942686)
作者简介:龙颖(1996-),男, 湖南岳阳人,硕士研究生,主要从事服装数字化技术方面的研究。
通信作者:邹奉元,E-mail:zfy166@zstu.edu.cn
Extraction of minimum units of four-consecutive patternbased on adaptive template matching
LONG Ying1a, L Yexin1a, 2, GUO Ziyi1a, HUANG Zhenhua1a, ZOU Fengyuan1a,1b,1c
(1a. School of Fashion Design & Engineering; 1b. Key Laboratory of Silk Culture Heritage and
Products Design Digital Technology, Ministry of Culture and Tourism; 1c. Zhejiang Provincial Research
Center of Clothing Engineering Technology, Zhejiang Sci-Tech University, Hangzhou 310018, China;
2.College of Creative Arts, Jinhua Polytechnic, Jinhua 321000, China)
Abstract: In order to realize the automatic extraction of minimum units of concatenated and overlapped four-consecutive patterns, this article iterated on the ratio of side length of rectangular template and investigated its impact on global template matching. The vertical vector method was adopted to analyze the center point set of the rectangle obtained from matching. The correspondence between the repetition law of pixels and the minimum unit was revealed. The accuracy of extraction results was measured by similarity mean, and the relationship between repetition times of minimum unit and similarity mean was clarified. By analyzing the applicability of template matching, an adaptive threshold template matching method was put forward. The average similarity can reach 94.29% after improvement. The results show that this method can effectively achieve the extraction of minimum units of concatenated and overlapped four-consecutive patterns.
Key words: extraction of minimum units; adaptive template matching; four-consecutive pattern; similarity matching; histogram similarity
織物花型是一种实用性与装饰性相结合的艺术形式,四方连续纹样是其中重要组成部分。四方连续纹样是通过单位纹样沿水平及垂直方向重复出现所产生的图案,而最小单元是表征四方连续花型周期性的重要参数。利用图像处理技术研究织物花型最小单元主要包括纹理最小单元识别和图案最小单元识别两类。第一类,纹理最小单元识别主要包括空间域和频域[1]:相对于以长度为自变量的空间域而言,频率域以频率为自变量进行图像信息表征,对噪声更为敏感,且处理更为简单。此外,不同学者针对色纱[2]、织物图像偏转[3]及纱线变形[4]等问题对纹理最小单元识别的干扰,提出了相应的解决方法。第二类,有Tao等[5]利用相似空间识别图案连续性,将图案分成单独、二方连续和四方连续;景军锋等[6]利用二维距离匹配函数计算规则织物图案的最小单元,来实现自动化检测图案最小单元并评估织物的质量;Kuo等[7]利用图案中元素中心提取最小单元,并在后续的研究中[8]考虑样本图案中元素存在的颜色、大小、旋转等变化。目前纹理最小单元识别方面的研究已经趋于完整;图案最小单元识别即四方连续纹样的花型最小单元提取,四方连续纹样按纹样中元素的连续关系,可分为散点式、连缀式及重叠式3种组织形式[9],相关学者通过不同方法研究了四方连续纹样最小单元识别,但多聚焦于散点式四方连续纹样,散点式四方连续纹样元素间存在明显的间隔,而连缀式及重叠式四方连续纹样,元素间存在连续性,导致最小单元分割识别困难。
针对连缀式及重叠式四方连续纹样,利用自适应阈值模板匹配,拟将连续特征转化为能替代花型重复规律的点集,避免直接对连续元素的分割;再采用垂直矢量法对点集进行分析,获取图像最小单元,以表征该类图像的周期性。为方便描述,将这两种纹样统称为花型连续纹样。
1 实 验
1.1 实验样本
由于目前暂无四方连续纹样样本库,主要针对四方连续纹样的3种组织形式中较复杂的连缀式及重叠式四方连续纹样,共采集连缀式及重叠式四方连续纹样样本各20个。两种组织形式纹样典型样本如图1所示。
在相似性匹配之前,首先需要对样本进行图像预处理,以去除纹理噪声以及织物色彩对图像分割的影响,主要包括灰度化、平滑及二值化处理。
1.2 相似性匹配
织物花型最小单元实质上是最小单元中的元素在上下左右4个方向上周期性的重复,因此任一元素都应符合同一重復规律,如图2所示。针对散点式四方连续,利用矩形框定位图中元素,并以矩形框任意点(这里以中心点为例)的重复规律识别出最小单元。
当花型连续时,各元素之间没有明显的界限,不能准确定位图像中某一元素的中心点,因此拟定一个一定大小的矩形框,以该矩形模板在图像中进行相似性匹配。
图像相似性匹配能根据已知模板,去寻找目标图像中的一个或多个相应模式的一种算法[10]。模板匹配是目前使用范围最广的相似性匹配算法之一,本实验通过最佳矩形模板迭代实验确定模板,比较匹配时模板与原图像所对应像素的灰度值,采用归一化互相关匹配法,将灰度值的相似性归结为向量间的相似性,并计算二者的匹配程度。相关性度量如式(1)所示:
R(i,j)=
∑Ms=1∑Nt=1Si,j(s,t)-E(Si,j)·T(s,t-E(T))∑Ms=1∑Nt=1Si,j(s,t)-E(Si,j)2·∑Ms=1∑Nt=1T(s,t)-E(T)2(1)
式中:E(Si,j)、E(T)分别表示(i, j) 处的子图及模板的平均灰度值。
使用最大类间方差法找到适合图像匹配的一个阈值[11],并将该值归一化,作为模板匹配时相关系数计算的初始阈值。若匹配时相关系数R(i,j)大于该值,则认为该矩形是矩形模板的相似矩形。在整个模板匹配过程中重复该过程,从而得到与模板矩形相似的多个矩形。
1.3 垂直矢量法
通过模板匹配完成相似性匹配后,定位矩形中心点,用矩形中心点代替匹配到的矩形,构成中心点点集。依据中心的点横纵坐标进行排序,将最靠近图像中心的点确定为原点O。从原点到图像范围的半径内,运用垂直矢量法搜索离原点最近的一个点A,确定OA向量。以OA向量为基准,搜索到满足与OA向量垂直且距离原点最近的点B。即OA与OB构成垂直夹角。夹角计算公式如式(2)所示:
θ=arccos(ABAB)(2)
在点集中,点位置可能存在一定误差,因此在判断垂直夹角时必须考虑误差(允许误差为:90°±1.5°)[8]。垂直矢量法如图3所示,OA与OB向量能确定一个近似矩形,根据OA与OB之间的夹角和距离得到一个近似矩形,所获取的近似矩形四个方向均符合四方连续的规则,且不存在再次连续的情况。在实际生产活动中最小单元多为矩形,故将近似矩形进一步处理,使其夹角为直角,以该矩形确定原图中相应位置,获取最小单元图像,从而实现花型连续纹样最小单元提取。
2 结果与讨论
2.1 矩形模板最佳占比迭代
为探究相似性匹配实验中矩形模板大小对结果的影响,以图1(b)为例进行矩形模板最佳占比迭代,拟得到矩形模板大小与结果之间的关系。因此需要对结果进行量化评价,而结果的准确性,实质是两个最小单元拼合时,拼合部分与样本中对应位置的相似性。采用直方图相似度来衡量相似性。如图4所示,将实验所得最小单元向四周平移,形成由9个最小单元组成的图像,以拼合线(粗线)向外侧延伸1/2最小单元的边长,并计算其与原图对应位置的直方图相似度。
针对单一图像,度量实验会呈现4个相似度值r(-1< r <1)构成的数组,以该数组的平均值对提取结果进行评价,称之为相似度均值。相似度均值越接近1,提取效果越好,反之越差。
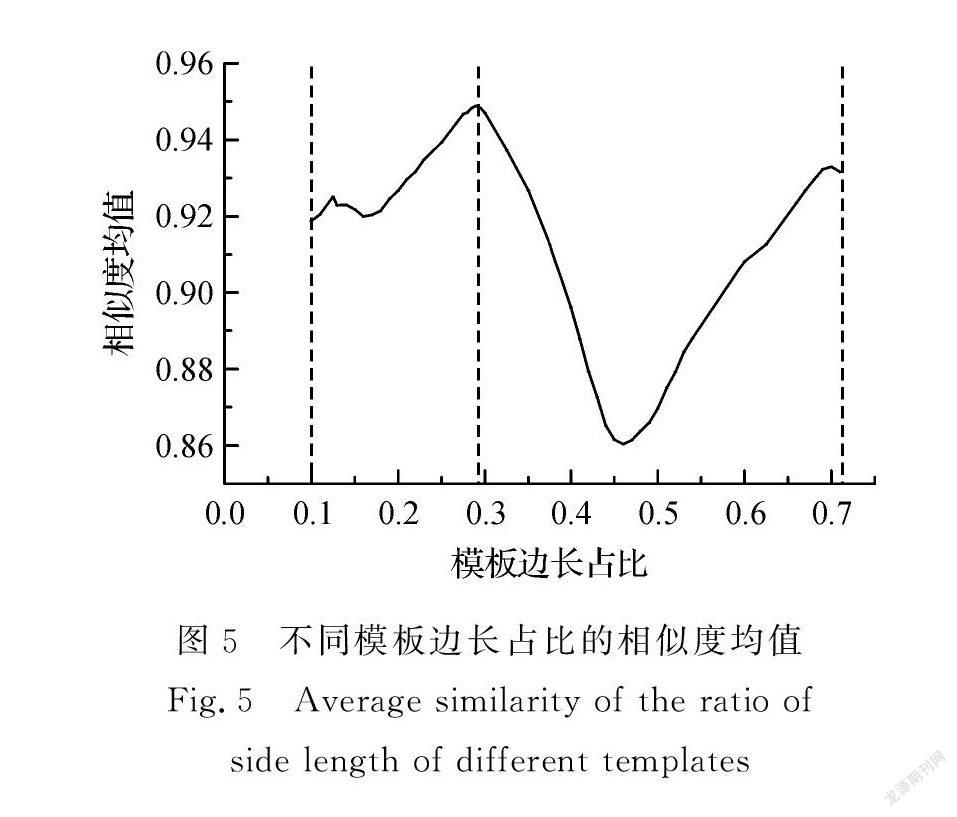
对于矩形模板大小,不同纹样之间存在差异,因此提出矩形模板最佳占比,拟寻找不同纹样间模板匹配时的统一性。矩形模板最佳占比是指相似度均值最大时,矩形模板边长所占原图像较短边长的比例。对矩形模板边长占比在区间(0, 1)进行迭代实验,其与相似度均值的关系如图5所示。
由图5知,矩形模板边长占比小于0.10或大于0.71时,超出了模板匹配的阈值,匹配无法进行;矩形模板占比迭代结果显示,使相似度均值最大的占比约为0.29。从40个样本中随机选取6、9、12、15个样本形成梯度,重复上述矩形模板最佳占比迭代实验,实验结果如表1所示。
如表1所示,随着样本数的增加,最佳占比区间趋于稳定。在样本数量为12、15时,最佳占比区间为(0.21, 0.38)。为方便实验进行,将矩形模板边长占比定为0.30。对于出现异常的样本,对比边长占比为0.30时,相似度均值与最大时的差值均小于0.005,因此取0.30为模板边长占比对该实验具有普适性。
确定矩形模板边长最佳占比后,为探究方法对不同样本的普适性,依据矩形模板与最小单元大小关系将样本分为三类:(Ⅰ) 模板包含最小单元;(Ⅱ) 模板与最小单元重合;(Ⅲ) 模板含于最小单元。三类关系典型样本如图6所示,样本(a)、样本(b)和样本(c)分别属于Ⅰ、Ⅱ和Ⅲ类。按照如上分类方式,40个样本中Ⅰ、Ⅱ和Ⅲ类分别有17、9、14个。
2.2 最小单元不同重复次数的适用性
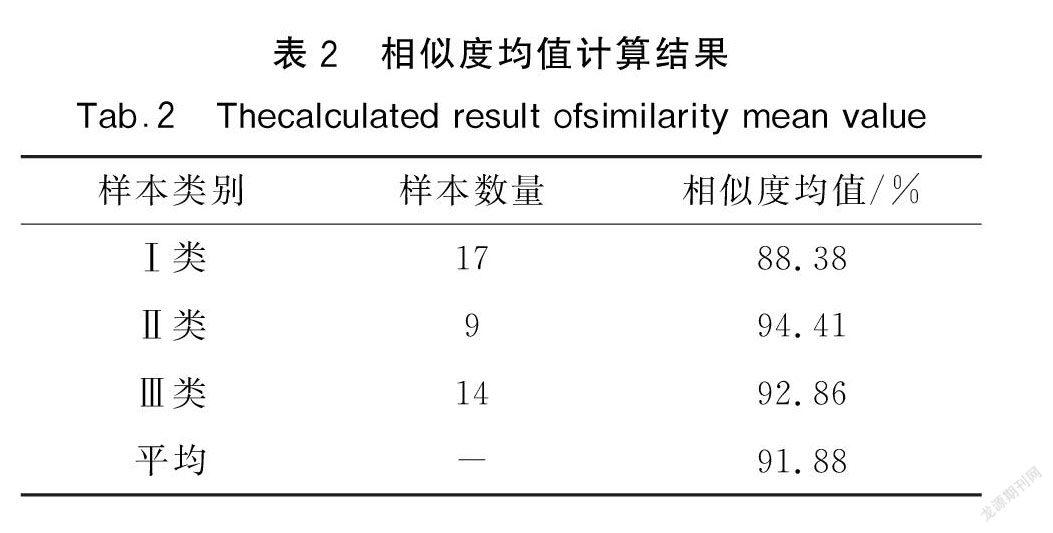
对40个四方连续纹样样本进行了识别,其相似度均值结果如表2所示。
由表2可知,相似度均值平均可达91.88 %,能较好达到预期结果;通过对比三类样本的相似度均值,Ⅰ类样本相似度均值较其余两类样本低。为探究该现象出现原因与纹样最小单元重复次数是否相关,以图6(a)为例,保持纹样不变,控制纹样最小单元在长、宽两个方向上的重复次数,生成5个图像分别属于三类样本。
不同重复次数的四方连续纹样如图7所示,从左至右最小单元重复次数依次降低,其中图7(a)、7(b)属于Ⅰ类,7(c)属于Ⅱ类,7(d)、7(e)属于Ⅲ类。其相似度均值依次为:87.62 %、89.53 %、94.7 %、92.71 %、92.59 %。结果表明,保持纹样不变时,Ⅰ类样本相似度均值仍偏低;结合最小单元提取过程发现,在模板匹配过程结束后,Ⅰ类样本中所匹配的矩形间存在交叉关系,对后续最小单元提取造成了一定干扰,使得该类样本相似度均值偏低。Ⅰ类样本表现为最小单元重复次数的增加,因此该方法更适用重复次数少的四方连续纹样,且在重复次数为3到4时(即最小单元与模板重合时),相似度均值最大。
2.3 自适应阈值
因不同图像自身信息差异,其模板匹配最佳匹配阈值存在差异,即通过最大类间方差法能确定初始阈值,使模板匹配顺利进行,但存在优化的空间[11]。模板匹配是根据模板以及原始图像之间的灰度值计算相关系数,再以匹配阈值来筛选相似矩形实现,而相关系数的计算是结合模板与其所覆盖待匹配的区域整体的灰度值进行计算,图像所包含的灰度值信息将直接影响匹配结果,图像差异对模板匹配的阈值设定有要求。为进一步提升最小单元提取结果的准确性,综合匹配原理与分析结果,提出自适应阈值模板匹配的方法,即同时考虑不同阈值下最小单元提取结果的准确性,采用直方图相似度对提取结果进行评价,获取最小单元最优解。
为缩减阈值k范围,综合比较不同阈值下的相似度均值。当k取0.1、0.2时,无法获取匹配点[12],k 0依次取值0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0,8个水平下不同样本的相似度均值如图8所示。
如图8所示,直方图相似度最大时阈值均落在0.6~0.8之间,为进一步提高阈值选取的合理性,在0.6~0.8范围内,步长为0.01进行遍历,固定阈值与自适应阈值相似度均值对比如表3所示。
由表3可知,3类样本自适应阈值时相似度均值均有提高,改进后相似度均值平均可达94.29 %,提升了2.41 %。结果表明,利用自适应阈值模板匹配算法提取花型连续纹样的最小单元,其结果更为准确。
为验证该方法对花型连续纹样最小单元匹配的普适性,实验选取三类样本各一个进行实验,其相似度均值分别为89.18 %、96.01 %、95.22 %,结果表明,该方法对Ⅱ、Ⅲ类样本更为适用。样本及提取结果如图9所示。
3 结 论
基于模板匹配提出一种识别连缀式及重叠式四方连续花型最小单元的方法。结果表明:模板匹配过程中,相似度均值最大时,矩形模板边长最佳占比区间为(0.21, 0.38);该方法更适用重复次数少的四方连续纹样,且在重复次数为3到4时,相似度均值最大;根据模板匹配阈值与相似度均值之间的关系,提出自适应阈值模板匹配的方法,改进后相似度均值平均水平提高到了94.29%。
参考文献:
[1]陶晨,周赳,奚柏君.织物图案连续性识别[J].纺织学报,2016,37(8):37-40.
TAO Chen, ZHOU Jiu, XI Bojun. Continuity identification of fabric patterns[J]. Journal of Textile Research, 2016, 37(8): 37-40.
[2]ZHANG J, PAN R R, GAO W D, et al. Automatic recognition of the color effect of yarn-dyed fabric by the smallest repeat unit recognition algorithm[J]. Textile Research Journal, 2015, 85(4): 432-446.
[3]XIAO Z T, GUO Y M, GENG L, et al. Automatic recognition of woven fabric pattern based on TILT[J/OB]. Mathematical Problems in Engineering, 2018: 9707104. https://doi.org/10.1155/2018/9707104.
[4]ZHENG D J, WANG L H. Multi-scale density detection for yarn-dyed fabrics with deformed repeat patterns[J]. Textile Research Journal, 2017, 87(20): 2524-2540.
[5]TAO C, ZHOU J, YIN M F. Automatic identification of textile pattern consecutiveness based on similarity space[J]. Textile Research Journal, 2017, 87(2): 224-231.
[6]景軍锋,杨盼盼,李鹏飞.采用距离匹配函数的印花织物图案周期测定[J].纺织学报,2015,36(12):98-103.
JING Junfeng, YANG Panpan, LI Pengfei. Determination on design cycle of printed fabrics based on distance matching function[J]. Journal of Textile Research, 2015, 36(12): 98-103.
[7]KUO J, SHIN C Y, LEE J. Repeat pattern segmentation of printed fabrics by Hough transform method[J]. Textile Research Journal, 2005, 75(11): 779-783.
[8]KUO J, LEE C L, SHIH C Y. Image database of printed fabric with repeating dot patterns part (I)-image archiving[J]. Textile Research Journal, 2017, 87(17): 2089-2105.
[9]刘兆辉,张华熊,林翔宇.基于内容特征的四方连续纹样自动生成[J].计算机系统应用,2019,28(5):156-160.
LIU Zhaohui, ZHANG Huaxiong, LIN Xiangyu. Automatic generation of quadrangle continuous patterns based on content characteristics[J]. Computer Systems & Applications, 2019, 28(5): 156-160.
[10]赵启.图像匹配算法研究[D].西安:西安电子科技大学,2013.
ZHAO Qi. Research on Algorithm of Image Matching[D]. Xi′an: Xidian University, 2013.
[11]OTSU N. A threshold selection method from gray-level histograms[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1): 62-66.
[12]汪会,孙洁,丁笑君,等.織物纹样特征提取与匹配方法比较[J].纺织学报,2020,41(4):45-50.
WANG Hui, SUN Jie, DING Xiaojun, et al. Comparison of feature extracting and matching methods for fabric patterns[J]. Journal of Textile Research, 2020, 41(4): 45-50.
