核心素养背景下的小学数学习题设计的三种策略

余文琳

在数学教学中，练习是不可或缺的部分。传统的习题设计注重对学生知识与技能的考查，起到巩固新知，静态反馈学生学习状态的作用。而在核心素养的背景下，数学题的设计不仅肩負对学生知识能力的考查，而且能够动态地推动学生思维的更深发展，提高学生的核心素养。因此，练习的设计尤为重要。如何才能有效设计练习，提高学生的核心素养呢？

一、立足知识本质，思辨中培养学生的核心素养

《义务教育数学课程标准（2011年版）》在评价建议中指出，要注重考查学生对基础知识和基本技能中所蕴含的数学本质的理解，以及能否在具体情境中合理应用。在以往的应试教育中，对知识的概念往往以这样的练习让学生强化记忆知识。如，在学完梯形的概念后的巩固练习，会以这样的练习来巩固知识：（  ）的图形叫作梯形。这样形式化的练习仅仅是将数学概念作为一个名词来教学，学生只是“接受”知识，虽然可能对梯形的概念记得滚瓜烂熟，但还是不得其意。而同样的知识练习，如果这样编制，不仅巩固所学的概念，还会提高学生的思辨能力。

如，如下图，在一张方格纸上画了5个图形，其中是梯形的有（  ）。

A.①⑤  B.①③⑤  C.①②④⑤  D.①③④⑤

在完成这道练习时，学生就必须调动所学的梯形的概念——“只有一组对边平行的四边形”，同时还要调动平行四边形的概念来比较它们的异同，并且认识到这些不同的概念所对应的不同解释，同时将这些概念在这5个图形中一一辨析，得出结论。通过这样的练习，避免了以偏概全的弊端，使学生不仅掌握了像①⑤这样的标准位图的梯形，而对像③④这样非标准位图的梯形也有了深刻的印象。通过这样的练习让学生明确了解决这样的问题必须关注概念的本质，从而提升学生的思维品质。

又如，在学习了分数，认识了后，为了让学生真正理解的内涵。可以设计这样的练习：你能用不同的方法在下面图形中表示出吗？对于每一种表示，解释你是如何知道你表示的阴影部分是的。

以往常常是借助分圆形蛋糕的情境来评价学生是否理解分数概念的。这样的评价是片面的，不能全面把握学生的认知情况。而以上的练习设计，开放了练习的答案，这样的练习让学生获得对分数的全貌认识，让学生充分地关注分数的概念本质，应用分数的概念，在更广阔的范围内表示出各种分数。并通过这样数形结合的认知，使思维推向更深的层次！

二、关注思维过程，体验中培养学生的核心素养

学生的数学学习不能仅仅是掌握一些概念和技能，而必须经历探索、猜想、推理等过程，解决有关的问题。《义务教育数学课程标准（2011年版）》明确把“形成解决问题的一些基本策略”作为一个重要的课程目标，为此，在我们的数学练习中要关注学生知识的形成过程，期望学生能够使用解决问题的方法调查和理解学习内容，即从解决问题的过程中学习数学，并尝试从不同角度分析问题，发展和应用各种策略解决问题，从而体验思维的养成过程。

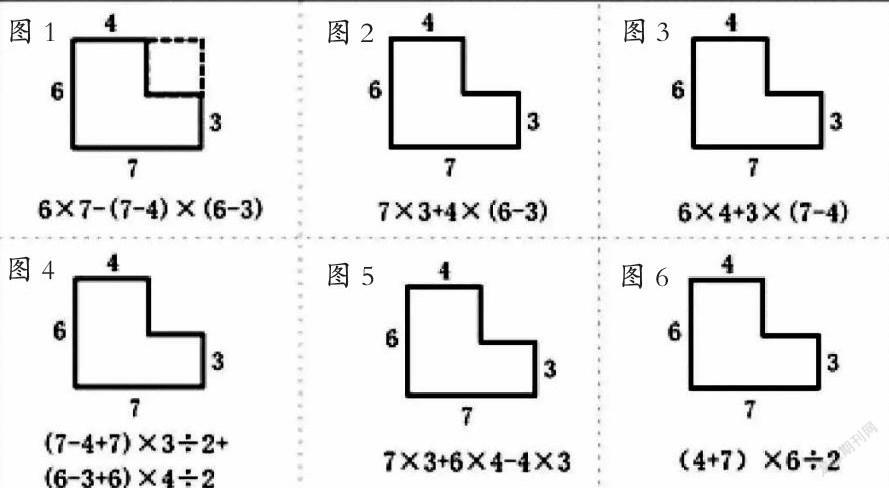
如，在学习了组合图形的面积后，可以通过这样的一组练习升化学生的思维品质。小明同学在求下图的图形面积时使用了6种不同的解决方法。图1的虚线表达了它的解法，其余的5种做法你能像图1一样用虚线表达对应的解题方法吗？

这样的一道题，并没有让学生动手去计算图形的面积，而是通过让学生根据算法来表示分法。这就要求学生不仅懂得算法还要深得其算理。通过对每一种算法中每一步算理的研究得出对应的分法，让学生的思维得到进一步的深入。这么多种的解法研究不再是课堂上简单的欣赏其他同学的做法，而是在参与深入的研究中真正拓宽了学生的思维维度，从而在思维的深度和宽度中升华其思维品质！

上述的练习对于大部分的学生来说具有一定的挑战性。当然教师在设计练习时也可以在一道题中让程度不同的学生的思维品质都得到肯定。在学习了三角形按角分类后，也可以这样设计练习：

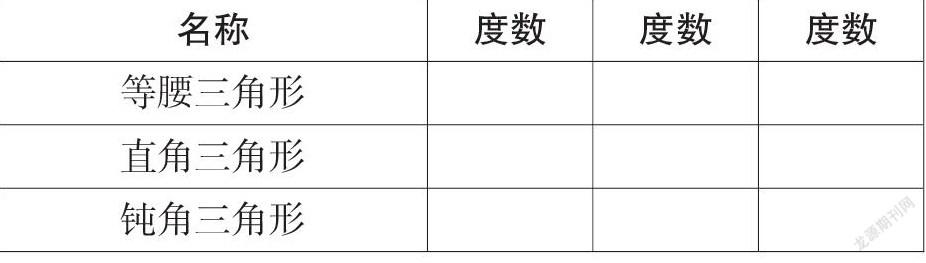
有3个不同的三角形，分别为等腰三角形、直角三角形和钝角三角形，这3个三角形一共有9个角，分别为70°，80°，90°，50°，20°，40°，50°，110°，30°。这3个三角形每个角分别是多少度？填在下面的表格里：

这道题打破了传统对于这方面知识的练习设计方式，不是已知角1、角2的度数，求角3的度数的填空题或选择题的形式，而是采用表格的方式呈现在学生们的面前。它不是单一的一个问题指向一个知识点，而是将三种三角形的特征及求第3个内角的度数这四个问题融合在一起，体现知识的内在联系。这道题虽然考查的是很简单、基础的知识，但学生的思维过程并不简单。它既可以考查学生是否具有策略意识，还需要调动学生的综合考虑问题的能力。面对这9个数据，学生首先要对这几个数据进行全面分析，这就要求学生要有数据分析的观念;还要将所学的各种三角形的特征和这些图形的度数对应联系起来，这里需要他们的应用意识;通过确定的角度求出第三个角的度数，这里需要一定的运算能力;如果出现问题，他们要反思自己先前的选择是否正确、如何调整，这里需要一定的推理能力。通过像这样类型的练习，很好地帮助学生主动地调动多方位思维，获得良好的数学素养。

三、融合趣味元素，浓情中促成学生核心素养的养成

“兴趣是最好的老师”，不管哪门学科的学习，这是颠扑不破的真理。数学作为培养人的逻辑思维和动手应用能力的基础课程之一，更应该遵循趣味性原则。新课标强调“以学生为本”的教学理念，数学作业的布置也要充分考虑到学生的需要和兴趣。而将每道枯燥的习题变身趣味的题型，对于教育者来说非常费时也并不那么容易。其实，有时在枯燥的练习中增添点情感因素，学生也就会兴趣盎然。

如，在学完小数乘法，探索发现乘数大于1、等于1和小于1时积的变化规律后有这样的练习：

先想一想积比第一个乘数大还是小，再计算。

0.12×50  2.6×0.5  1.3×2.2  9.6×0.8

教师以第一道0.12×50为例，说0.12先生出门遇见了乘数50先生，0.12先生高兴吗？此时，枯燥的题目显得生动起来，在趣味中学生对知识的运用往往发挥得更好。当学生回答“高兴”时，追问：“为什么？”学生在说出规律的同时，巩固了新知。接着，教师再次追问，“那50先生高兴吗？”“为什么？”显然，在趣味中，学生已经超常发挥完成题目中的问题，能思辨两个乘数与积之间的变化规律。而且，给枯燥的习题增添情感因素后，学生对这种练习题及习题背后的知识本质记忆犹新，不易忘却。

又如，学习三角形边的关系一课。当学生学会三角形任意两边之和大于第三边，进行“判断线段6cm，9cm，12cm是否能组成三角形？”练习时，教师可以赋予三边有趣的角色。“12cm相当于“‘地主中的地主，6cm和9cm联合能斗得过地主吗？”听到老师将枯燥的练习同有趣的“斗地主”游戏巧妙地联系起来，学生的兴趣和思维瞬间被点爆并绽放。学生开心地回答“能！”。再次判断其他类似题时，学生便能又快又准地回答。而且，像这样给枯燥的习题增添情感因素后，学生对这种练习题及习题背后的知识本质记忆犹新，不易忘却。

作为一线教师，要善于从培养学生良好数学素养的角度编制习题，编制时要考虑它的知识性、思维性和趣味性，以此有效地发挥习题在促进学生数学思考方面的功能作用，从而能更好地拓展学生的思维，提高学生解决问题的能力，提升学生的数学素养，促进学生的全面发展！