气动折入边装置中纱线初始位置对折边效果的影响

刘宜胜， 周鑫磊， 刘丹丹

(1. 浙江理工大学 机械与自动控制学院， 浙江 杭州 310018； 2.浙江大学 生物医学工程与仪器科学学院， 浙江 杭州 310027； 3. 浙江众合科技股份有限公司 中央研究院， 浙江 杭州 310051)

自19世纪以来，无梭织机技术[1]愈发成熟，轻巧、高产、优质、低耗、低振动、低噪声、快车速的新型无梭织机[2]受到市场青睐。无梭织机织造采用机外供纬，不像有梭织机是机内供纬，可连续投纬，故经其加工后的布边通常无法直接形成光边[3]，而折入边装置可使织物呈现光洁硬挺的折入边，被广泛地应用于工业生产[4]。折入边装置主要有机械式[5]和气动式2种。随着气动式自动化水平的高速发展，适用于高速织机的气动式优势明显。21世纪以来，国内外对气动折入边装置进行了大量的研究。德国Dornier公司提出的多尼尔气动折入边装置大幅度提升了喷气织机的性能极限。其结构上不存在可移动零部件，功能上提供了气动折入边单元，增设了折入边控制单元。宋日升等[6]开发了一种气动折入边装置，在织造阶段可将剪断后外露的纬纱经压缩空气适时折入布边组织，装备结构简单紧凑，没有运动部件，高效光边。

近年来，研究者们广泛研究了纱线在气流场中运动的规律。Guo等[7]指出标准的K-ε双方程湍流模型忽略了流线曲率效应引起的各向异性黏度和额外湍流的产生，无法模拟受限旋流，于是提出采用一种可实现的K-ε湍流模型来模拟开槽管喷嘴内的流动特性。此模型是一个涡流黏度模型，由新的模型耗散率方程和由Shih等[8]提出的新的可实现的涡黏性公式组成。Hassana等[9]建立了一个计算流体力学模型来模拟空气喷嘴内部的气流行为，研究、分析、预测和控制旋转气流行为对纤维运动和纱线性能的影响。纱线极高的长径比、一定的柔性、外观形态的均匀性、内在组成质量和分布的连续性及纤维间相互作用的稳定性等结构要求给三维建模带来了巨大挑战。Jonathan等[10]将纱线模拟成一根具有抗弯曲能力的不可延伸的曲线；Osman等[11]把柔性纤维丝视为由一系列杆元件连接的数字链，在有限元分析里选用弹性杆单元来简化模型。在研究气动折入边装置方面，刘宜胜等[4,12]建立了二维流固耦合模型来模拟不同长度的纱线在气流作用下的折边过程，研究了10 mm的纱线在不同角度气流作用下的运动规律。气流场中纱线的运动属于三维流固耦合范畴，然而以往的研究大都基于气动折入边装置二维流固耦合和喷嘴结构等方面的研究，对气动折入边装置中的纱线受气流场多方位作用的三维流固耦合仿真运动分析很少，尤其是纱线初始位置对纱线折入的影响。

本文采用考虑气流场与纱线相互作用的单向流固弱耦合算法，建立了纱线先后在斜吹和折入气流作用下大变形的三维数值模型来模拟一端固定另一端自由的单根纱线折入过程的行为。为进一步验证此数值模型的准确性，构建了可视化实验平台，通过分析初始位置不同的5组纱线先后在斜吹和折入气流作用下的运动规律，深层次探索纱线的折入机制，为优化实验装置提供理论参考。

1 单向流固弱耦合算法的数值模拟

流体域部分是采用机械三维设计软件SOLIDWORKS构建出气动折入边装置的三维气流场流体模型，并用有限元分析软件FLUENT中的realizableK-ε湍流模型来描述三维可压缩黏性气体的高速流动情况。固体域部分是把纱线离散成连续弹性梁单元组成的数字链。通过独立开发的JAVA程序仿真软件将FLUENT和ABAQUS联合，建立起一个考虑气流场与纱线相互作用的单向流固弱耦合模型来模拟一端固定另一端自由的单根纱线在气动折入边装置工作区域中先后在斜吹和折入气流作用过程中的运动行为。

本文采用反距离加权插值算法提取气流场中纱线固体模型每个梁单元节点处的气流速度，并通过白金汉Π定理总结出的方程将其转化为对应单元节点的气动力施加在纱线模型对应的单元节点上，最后通过显式动力学算法对受气动力等外力作用的纱线进行位移、形变的计算。其中由有限元分析软件FLUENT和ABAQUS的求解器分别求解流体模型的控制方程和纱线每个梁单元节点处的位移、形变，采用迭代算法计算获取每一时间步下纱线梁单元节点的位移、形变和气动力。

1.1 气动折入边装置三维气流场流体模型

气动折入边装置三维气流场流体模型如图1所示，由斜吹气流进气管道、折入气流进气管道、斜吹管道和4根折入管道组成。

图1 折入和斜吹三维气流场流体模型Fig.1 Tucked-in and oblique-blowing three-dimensional airflow field fluid model

1.2 纱线固体模型

选用55 tex纯棉纱线(越南纺织服装集团东南股份公司)，纱线的直径为0.38 mm，密度为500 kg/m3，弹性模量为80 MPa,泊松比为0.307。

1.2.1 纱线有限元模型

纱线在气流场中受轴向力、弯矩和扭矩。纱线固体模型是把纱线离散成连续弹性梁单元组成的数字链，在有限元分析软件ABAQUS中选用空间弹性梁单元(beam)来简化。在纱线固体模型有限元分析中，纱线会被离散成连续的弹性梁单元，单元的质量都被分解到该单元的节点上。纱线模型属梁柱单元，不考虑剪切变形，考虑轴力、弯矩和扭矩产生的变形等。

1.2.2 显式动力学算法

显式动力学算法是基于动力学方程的显式算法，通过前增量步结束时的已知状态计算后增量步结束时的状态。显式动力学算法能精确求解的前提是增量步中的加速度趋近于常数，也就要求增量步无穷小。

1.3 单向流固弱耦合算法

单向流固弱耦合算法是多物理场之间信息交互的纽带，本文需要同时处理和求解气流场流体和纱线固体这类物理场之间的问题。

1.3.1 反距离加权插值

用反距离加权插值算法提取出纱线固体模型每个梁单元各节点处的气流场流场数据。

1.3.2 气动力

影响气流场中纱线运动行为最主要的因素是气流阻力。气流阻力大小主要和气流密度(ρ)、气流与纱线之间的相对运动速度(v)和接触面积(A)有关，可根据白金汉宫Π定理推出：

(1)

式中，F为气动力，N。

由力学工程经验公式可知，根据白金汉宫Π定理推演出的Π为阻力系数Cd，得气动力F公式：

F=Cdρv2A=Cdρv2dl

(2)

式中：l为长度，m；d为纱线圆形横截面的直径，m。

纱线在气流场里受到的气动力F可沿纱线的轴向和径向分解，可得：

(3)

(4)

式中：Ca为纱线轴向阻力系数；Cr为纱线径向阻力系数；va为轴向上纱线与气流的相对运动速度，m/s;vr为径向上纱线与气流的相对运动速度，m/s。

2 纱线折入可视化实验

2.1 可视化实验平台

为验证单向流固弱耦合算法的准确性，设计搭建了一个包含高速摄像机的可视化实验平台来捕捉纱线的运动。可视化实验平台主要包括气路和电路2部分，工作原理见图2。气路部分由空气压缩机产生高速气流先后通过电气比例阀和电磁阀进入气动折入边装置的斜吹气流进气管道和折入气流进气管道。电路部分由24 V开关电源持续为信号发射器、电气比例阀、电磁阀、欧姆龙可编程控制器供电；信号发生器对电气比例阀进行调压输出控制；欧姆龙可编程控制器通过电信号控制电磁阀的开与闭，从而实现斜吹和折入气流能对气动折入边装置里的纱线进行异步喷射，达到斜吹和折入气流异步作用于纱线的效果。

图2 实验平台工作原理图Fig.2 Working principle diagram of visual experiment bench

2.2 实验设置

选取5个合适但不同的初始位置，使用高速摄像机实时捕捉记录这5组纱线先后受初始气压都为0.4 MPa的斜吹和折入气流异步作用的运动行为。

斜吹管道轴线和4根折入管道中心线相互垂直。定义4根折入管道中心线水平向右为X轴正方向，斜吹管道轴线铅垂向上为Y轴正方向。规定斜吹管道轴线与4根折入管道中心线交于点O(12.5,13.95,10)，如图3所示。

图3 管道坐标图Fig.3 Schematic diagram of ducts

5组初始位置不同的纱线沿X轴正方向平铺放置，纱线长度为10 mm。纱线固定端的坐标依次为A组(8.5,19.5,10)，B组(10,19.5,10)，C组(11.5,19.5,10)，D组(10,21,10)，E组(10,18,10)。

3 数值模拟结果与分析

纱线的折入可分为2个阶段：一是纱线受气流场的斜吹气流作用运动至斜吹平衡状态的斜吹运动；二是处于斜吹平衡状态的纱线受气流场的折入气流作用完成折入过程，达到折入平衡状态的折入运动。纱线的斜吹运动和折入运动是一个连续过程。

3.1 斜吹和折入气流对气流场的影响

首先打开斜吹气流进气管道气流入口，斜吹气流进入初始状态为1个大气压的气流场后会影响其周围气流场的状态，包括气流场的速度和压力。然后关闭斜吹气流进气管道气流入口的同时打开折入气流进气管道气流入口，折入气流进入气流场后，同样也会影响其周围气流场的状态。图4示出斜吹气流气流场和折入气流气流场的速度和静压力分布云图。

图5(a)示出斜吹气流气流场在斜吹管道轴线处速度和压力与其离斜吹气流进气管道入口的位移之间的关系，图5(b)示出折入气流气流场在4根折入管道中心线处的速度和压力(其中4根折入管道区域内的数值用4根折入管道轴线处的平均值表示)与其离折入气流进气管道入口的位移之间的关系。

从图4(a)和图5(a)可看出，斜吹气流从斜吹气流进气管道气流入口射入气流场后，斜吹气流进气管道内(Ⅰ区域)的气流开始向Y轴负方向流动，流速慢，压力稳定，总压等于静压加动压。在斜吹气流的影响下，斜吹气流进气管道(Ⅰ区域)和斜吹管道(Ⅱ区域)交界区域的气流速度急剧增大，交界区域前后速度差距明显。因气动折入边装置斜吹气流进气管道的直径比斜吹管道大5倍，根据流体力学连续性方程可知,斜吹管道顶端(Ⅱ-A区域)气流速度可达斜吹气流进气管道流速的36倍左右；由于气流速度过快，根据流体力学伯努利方程可知，气流静压大幅度下降，动压上升。在斜吹气流持续地喷射下，斜吹管道顶部稍往后的管道区域(Ⅱ-B区域)里的气流会稳定下来，呈现回落现象，速度和气压小范围变化。斜吹管道剩余区域(Ⅱ-C区域)因斜吹管道两端存在气压差，在气压差的推动下，气流速度有缓慢上升趋势，至斜吹管道末端达气流速度峰值;静压有平缓下降趋势，到斜吹管道末端减小至0 MPa;动压有平缓上升趋势，至斜吹管道末端达动压峰值。

图4 气流场的速度和静压力分布云图Fig.4 Contours of velocity and pressure of flow field.(a) Oblique-blowing airflow field; (b) Folding-in airflow field

图5 速度和压力与位移关系图Fig.5 Diagram of velocity and pressure for displacement.(a) Oblique-blowing airflow field; (b) Folding-in airflow field

在斜吹管道(Ⅱ区域)和远离斜吹管道区域(Ⅲ区域)交界区域后部(Ⅲ-A区域)的气流速度减小，静压维持在0 MPa，动压变小。由于气流是从窄细的斜吹管道突然进入较大的无束缚的区域，当气流在此区域某位置达一定量时，就会形成一个小范围高压区，气流速度和压力会有小范围波动。远离斜吹管道区域(Ⅲ-B区域)的气流速度随远离斜吹管道而线性减小，静压基本维持在0 MPa，动压也同样随远离斜吹管道而线性减小。

折入气流通过4根折入管道喷射，而斜吹气流仅通过1根斜吹管道。从图4(b)和图5(b)可看出，折入气流从折入气流进气管道气流入口射入后，折入气流进气管道(Ⅰ区域)内的气流开始向X轴负方向流动。折入气流进气管道前部(Ⅰ-A区域)气流速度慢，压力稳定，静压略小于折入气流的初始气压0.04 MPa，动压略大于0 MPa，总压等于静压加动压，稳定在0.04 MPa。4根折入管道在折入管道中心线处没有与折入气流进气管道直接连通，而在中心线四周连通，且折入气流进气管道首尾两端存在气压差，所以折入气流进气管道后部(Ⅰ-B区域)气流在压差的推动下，向分布在4根折入管道中心线四周的4根折入管道里流动，此区域内4根折入管道中心线方向的气流速度线性减小，直至进气管道的尽头由于管道不通减为0 m/s，动压线性上升至折入气流的初始气压0.04 MPa，静压线性下降至0 MPa。

在折入气流的影响下，折入气流进气管道的气流全部进入4根折入管道，在折入气流进气管道(Ⅰ区域)和折入管道(Ⅱ区域)4块交界区域的气流速度急剧增大，交界区域前后速度差距大，气流压力变化程度也大，静压锐减，动压暴增。因折入气流进气管道的直径大于4根折入管道，根据流体力学连续性方程可知：折入管道顶端(Ⅱ-A区域)气流速度可达折入气流进气管道里气流速度的36倍左右，为气流速度峰值。由于气流速度过快，根据流体力学伯努利方程可知：气流静压大幅度下降，而动压上升，达动压峰值。在折入气流持续地喷射下，折入管道顶部往后的管道区域(Ⅱ-B区域)里的气流会逐渐稳定下来，有一个回落现象，气压小范围变化，静压会有小幅上升，同时动压也相应有小幅下降。折入管道剩余区域(Ⅱ-C区域)会因为斜吹管道两端存在一定的气压差，气流会在压差的推动下，速度有略微的上升趋势，静压会有平缓的下降趋势，直到斜吹管道末端减小至相对气压为0 MPa，动压也会有略微的上升趋势。

从4根折入管道射出的折入气流(Ⅲ区域)向4根折入管道中心线方向汇聚，气流在中心线处叠加，气流速度随远离折入管道而线性增加，静压维持在0 MPa，动压同样随远离折入管道而线性增加。

3.2 斜吹气流对纱线运动的影响

斜吹气流进入气流场，不仅影响其周围气流场的状态，还影响沿X轴正方向平铺放置纱线的状态。在数值模拟结果中选取5组纱线初始位置、受斜吹气流影响每一整毫秒的斜吹运动状态以及受斜吹气流影响达斜吹平衡状态进行对比分析，如图6所示。

图6 气流场中不同时间步下纱线的斜吹运动状态Fig.6 Oblique-blowing movement state of yarn at different time steps in airflow field.(a) Group A; (b) Group B; (c) Group C; (d) Group D; (e) Group E

从图6可以看出，纱线一开始都处于水平状态，呈现 “一”字型。斜吹气流影响气流场后，纱线中前部在斜吹气流作用下，开始向Y轴负方向运动，整根纱线呈现近似“V”字型的斜吹运动状态。渐渐地，纱线中前部向Y轴负方向运动加剧，纱线自由端也随纱线中前部向Y轴负方向运动，整根纱线呈现近似“U”字型的斜吹运动状态。随斜吹气流持续作用，纱线自由端向Y轴负方向运动加剧，也逐渐向X轴负方向运动，整根纱线呈现近似“2”字型的斜吹运动状态。长时间受斜吹气流作用的纱线会达斜吹平衡状态，整根纱线呈现近似“1”字型的斜吹运动状态。表1示出不同时间步下纱线的伸长量和X坐标为0.012 5 m的梁单元节点所受气动力情况。根据图6和表1可知：整个斜吹过程中，纱线会伸长，所受的气动力随远离斜吹管道而逐渐变小，作用范围逐渐变大。

表1 不同时间步下纱线的伸长量和X坐标 为0.012 5 m的梁单元节点所受气动力情况Tab.1 Elongation of yarn and aerodynamic force of beam element node whose X coordinate is 0.012 5 m at different time steps

5组初始位置不同的纱线在斜吹气流作用下，都能达斜吹平衡状态。初始位置向X轴方向适当移动，5组纱线所受气动力对纱线的力臂不等，导致纱线所受力矩不等。初始位置向X轴负方向移动，力臂变大，导致力矩变大，相同时间步的纱线向Y轴负方向弯曲程度变大，伸长量变大，且纱线达斜吹平衡状态需运动的距离变小，故斜吹过程所需时间也少。A组虽力矩大，但作用时间短；C组虽力矩作用时间长，但力矩小，所以斜吹过程纱线的总伸长量小于B组。

初始位置向Y轴方向移动，5组纱线所受气动力不等，作用范围也不等。初始位置向Y轴负方向适当移动，虽气动力变小，但作用范围变大，相同时间步的纱线在二者的共同影响下向Y轴负方向弯曲程度略微变大，伸长量略微变大，且纱线达斜吹平衡状态需运动的距离变小，故斜吹过程所需时间也略少，但由于减少时间总量不明显，所以斜吹过程的总伸长量略变大，但增加不明显。

综上所述，纱线初始位置向X轴和Y轴负方向适当移动，可缩短纱线完成斜吹过程所需时间，尤其改变初始横坐标，也影响纱线斜吹过程的伸长量。

3.3 折入气流对斜吹后纱线运动的影响

纱线在斜吹气流作用下达斜吹平衡状态，后折入气流进入气流场，影响其周围气流场状态的同时，也影响处于斜吹平衡状态纱线的状态。在数值模拟结果中选取5组纱线折入前的初始位置(斜吹平衡状态)、受折入气流影响0.5 ms整数倍的折入运动状态以及先后受斜吹和折入气流影响完成折入的折入平衡状态进行对比分析，如图7所示。

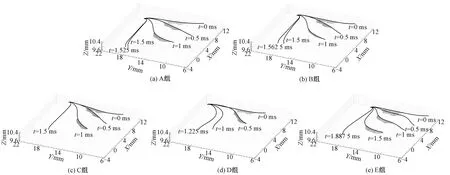
图7 气流场中不同时间步下纱线的折入运动状态Fig.7 Tucked-in movement state of yarn at different time steps in airflow field. (a) Group A; (b) Group B; (c) Group C; (d) Group D; (e) Group E

由图7可知，折入气流影响气流场后，经斜吹气流作用达斜吹平衡状态的纱线中后部在折入气流作用下，向X轴负方向运动。渐渐地，纱线中后部向X轴负方向运动加剧，纱线自由端也随纱线中后部向X轴负方向运动。随着折入气流持续作用，纱线自由端向X轴负方向运动加剧，也逐渐向Y轴正方向运动。长时间受折入气流作用的纱线会完成折入过程，达折入平衡状态。表2示出不同时间步下纱线的伸长量和Y坐标为0.013 95 m的梁单元节点所受气动力情况。根据图7和表2可知：在整个折入过程中，纱线会伸长，所受的气动力随远离折入管道而略微变化，作用范围逐渐变大。

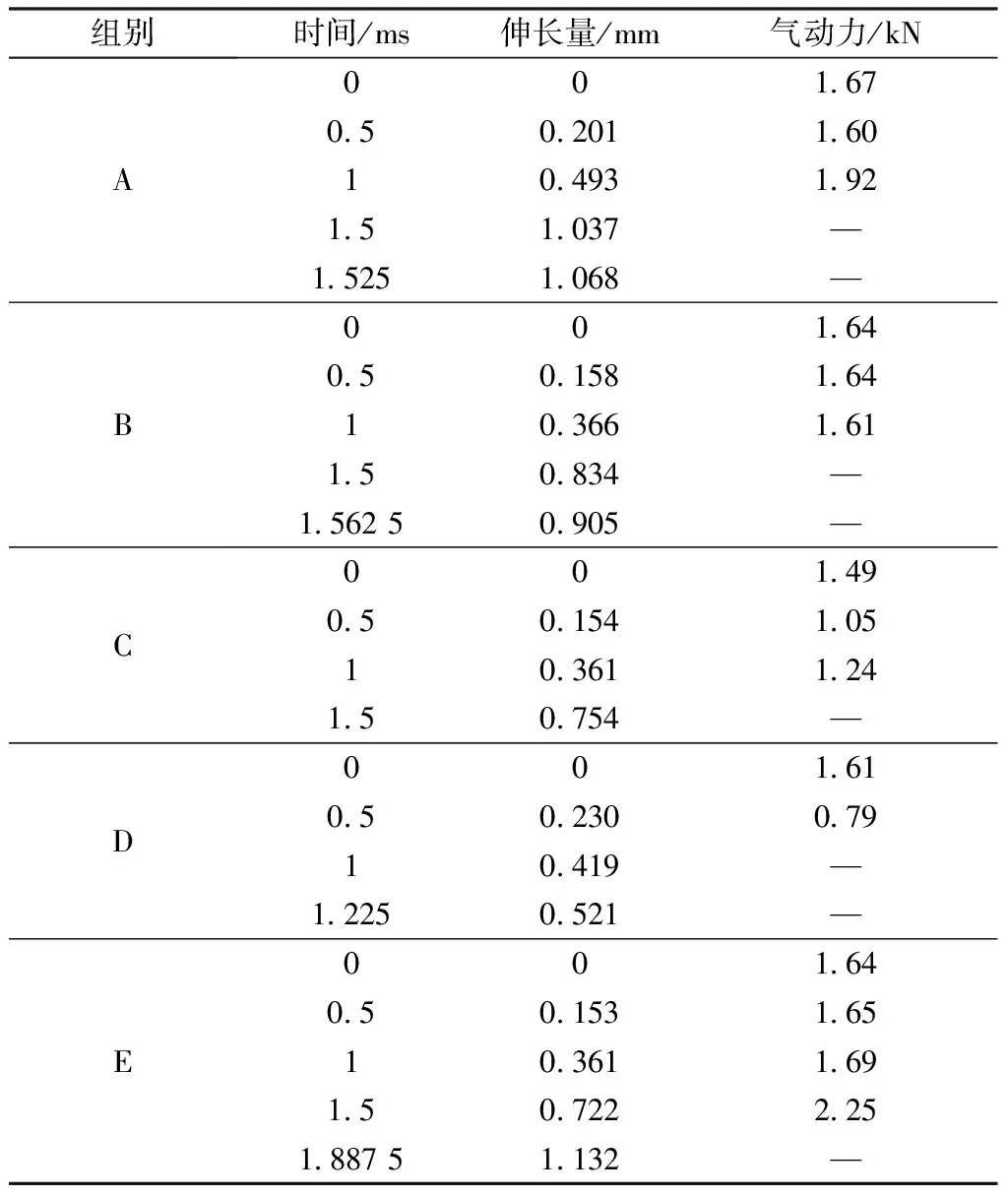
表2 不同时间步下纱线的伸长量和Y坐标为 0.013 95 m的梁单元节点所受气动力情况Tab.2 Elongation of yarn and aerodynamic force of beam element node whose Y coordinate is 0.013 95 m at different time steps

5组纱线先后受斜吹折入气流作用，都能在7.425 ms内完成折入，达折入平衡状态，但A、B和C组折入效果更好。初始位置向X轴方向适当移动，5组纱线所受气动力差距不大，作用范围不等。初始位置向X轴负方向移动，气动力稍大，前期气动力作用范围大，相同时间步的纱线向X轴负方向弯曲程度变大，伸长量变大，但后期气动力作用范围小，且斜吹平衡状态的纱线达折入平衡状态的距离变远，故折入过程所需时间差距不大，但总伸长量变大。

纱线初始位置向Y轴方向适当移动，5组纱线所受气动力对纱线的力臂不等，导致纱线所受力矩不等。初始位置向Y轴负方向移动，力臂变小，导致力矩变小，相同时间步的纱线向X轴负方向弯曲程度变小，伸长量变小，且斜吹平衡状态的纱线达折入平衡状态的距离变远，故折入过程所需时间增加，时间的增加导致折入过程的伸长量增大。

综上所述，纱线初始位置向Y轴正方向适当移动，可缩短纱线折入过程所需时间；初始坐标影响纱线折入过程的伸长量，纵坐标影响纱线折入效果。

4 可视化实验结果与分析

通过调节气动折入边装置的斜吹机构和折入机构，研究纱线初始位置对纱线折入的影响。高速摄像机下，5组纱线的折入轨迹如图8所示。

图8 实验中纱线的折入轨迹Fig.8 Tucked-in trajectory of yarn in experiment. (a) Group A; (b) Group B; (c) Group C; (d) Group D;(e) Group E

数值模拟和实验中的纱线完成折入后的总伸长量情况如表3所示。由于实验中纱线受气流作用时间远长于数值模拟，故实验总伸长量较大。

表3 纱线的总伸长量情况Tab.3 Total elongation of yarn

将离纱线固定端2.5、5和7.5 mm点的数值模拟和实验结果进行对比，得此3点的数值模拟和实验运动轨迹图，如图9所示。可以看出,5组纱线均能完成折入过程，A 组折入最快，E组伸长量最大，但A、B和C组折入效果更好。数值模拟中纱线折入过程的运动轨迹和实验中的基本吻合，单向流固弱耦合算法准确性较好。纱线初始位置会影响纱线的伸长量和纱线完成折入的总时间。适当将纱线初始位置向X轴负方向和Y轴正方向移动，可加速纱线的折入，尤其是改变初始横坐标。适当将纱线初始位置向X轴负方向和Y轴负方向移动，可提升纱线折入过程的总伸长量，尤其是改变初始纵坐标，且纱线的折入效果与初始纵坐标有关。

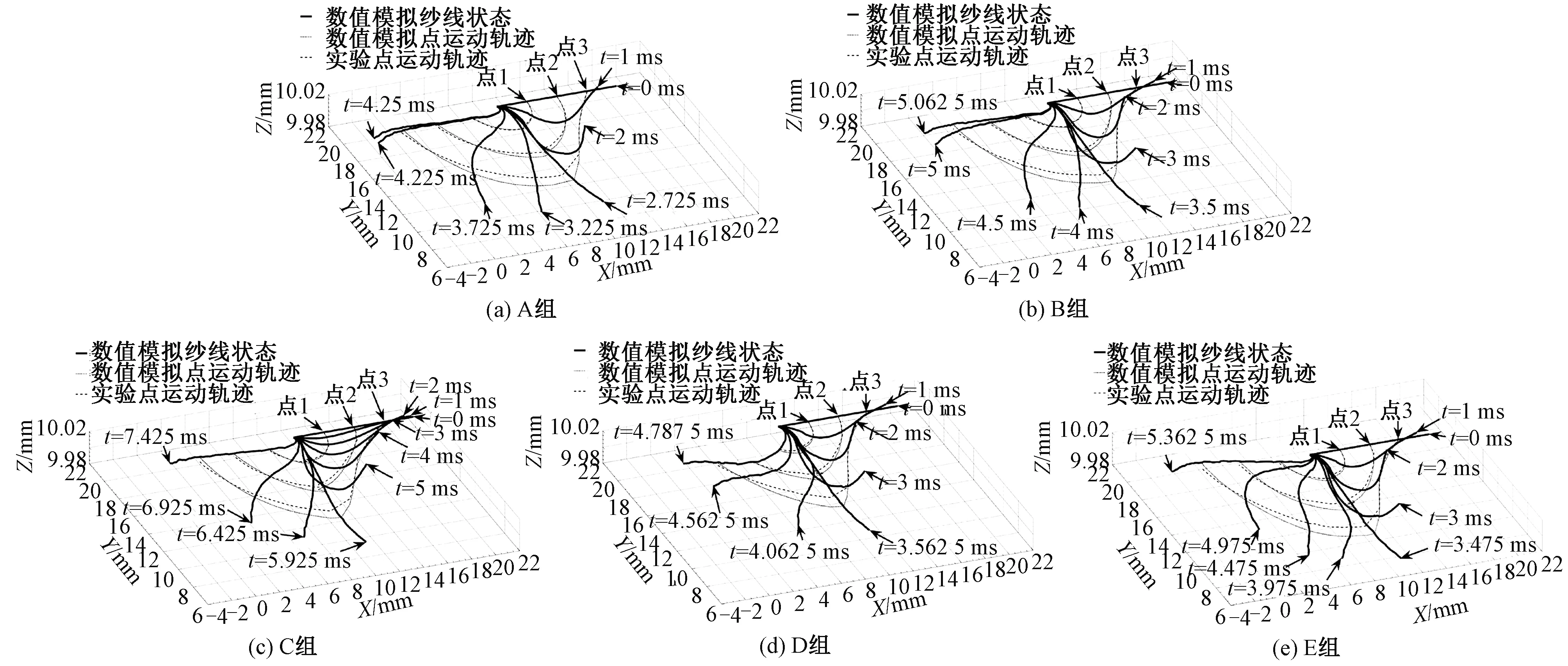
图9 3点的数值模拟和实验结果运动轨迹图Fig.9 Motion trajectory diagram of numerical simulation and experimental results of three nodes.(a) Group A; (b) Group B; (c) Group C; (d) Group D; (e) Group E

5 结 论

本文基于单向流固弱耦合算法的纱线折入过程数值模拟和可视化实验相结合的方法，验证了弱耦合算法的准确性，分析了5组不同初始位置的纱线空间运动状态的规律。结果表明：5组初始位置不同的纱线在斜吹和折入气流作用下均能在7.425 ms内完成折入；适当缩小纱线初始横坐标和增大纱线初始纵坐标可加速纱线的折入，尤其是缩小纱线初始横坐标；适当缩小纱线初始横坐标和缩小纱线初始纵坐标可使纱线折入过程的总伸长量变大，尤其是缩小纱线初始纵坐标；初始纵坐标影响纱线的折入效果。