升力式飞行器助推段多约束弹道优化设计

梁欣欣,王 惠,姜 威

(北京宇航系统工程研究所,北京 100076)

升力式飞行器一般在某一高度处入轨,通常采用多级固体运载器经助推段飞行将其助推至入轨点。由于整个助推段全部在复杂大气环境中飞行,弹道设计约束条件较多。助推段弹道设计除了要满足入轨条件外,还需提供尽可能大的入轨速度。目前,对于升力式飞行器的轨迹优化问题较多,多偏重于优化算法与优化方法研究,过程较为复杂、效率不高,工程应用可操作性不高。本文旨在基于工程设计方法,研究助推段轨迹优化的设计方法。

本文以三级固体运载器为研究对象,提出了升力式飞行器助推段弹道设计方法,建立了多约束下以入轨速度最大为目标的优化模型,并以牛顿迭代法确定初值,且以序列二次规划(sequential quadratic programming,SQP)法进行优化仿真。仿真获得了满足多约束条件下的优化解,验证了升力式飞行器助推段弹道设计方法的正确性和有效性。

1 助推段弹道设计方法

升力式飞行器助推段弹道具有飞行高度低、转弯角度大的特点,需要在入轨点处完成三级固体运载器从垂直向水平的转弯过程。三级固体运载器二级发动机为两挡变推力发动机,各级发动机均为耗尽关机方式,助推段一直在大气中飞行,飞行环境复杂,因此助推段弹道设计需尽可能提供较好的飞行环境。根据各级飞行特点,进行助推段俯仰程序角设计,设计结果如图1所示。图中,,,分别对应各级攻角转弯时的最大负攻角;(=0,1,…,8)为各阶段时刻点,为二级飞行两档推力间的无动力滑行时间,为二三级分离后无动力滑行时间;,,分别为对应定轴飞行的俯仰程序角。

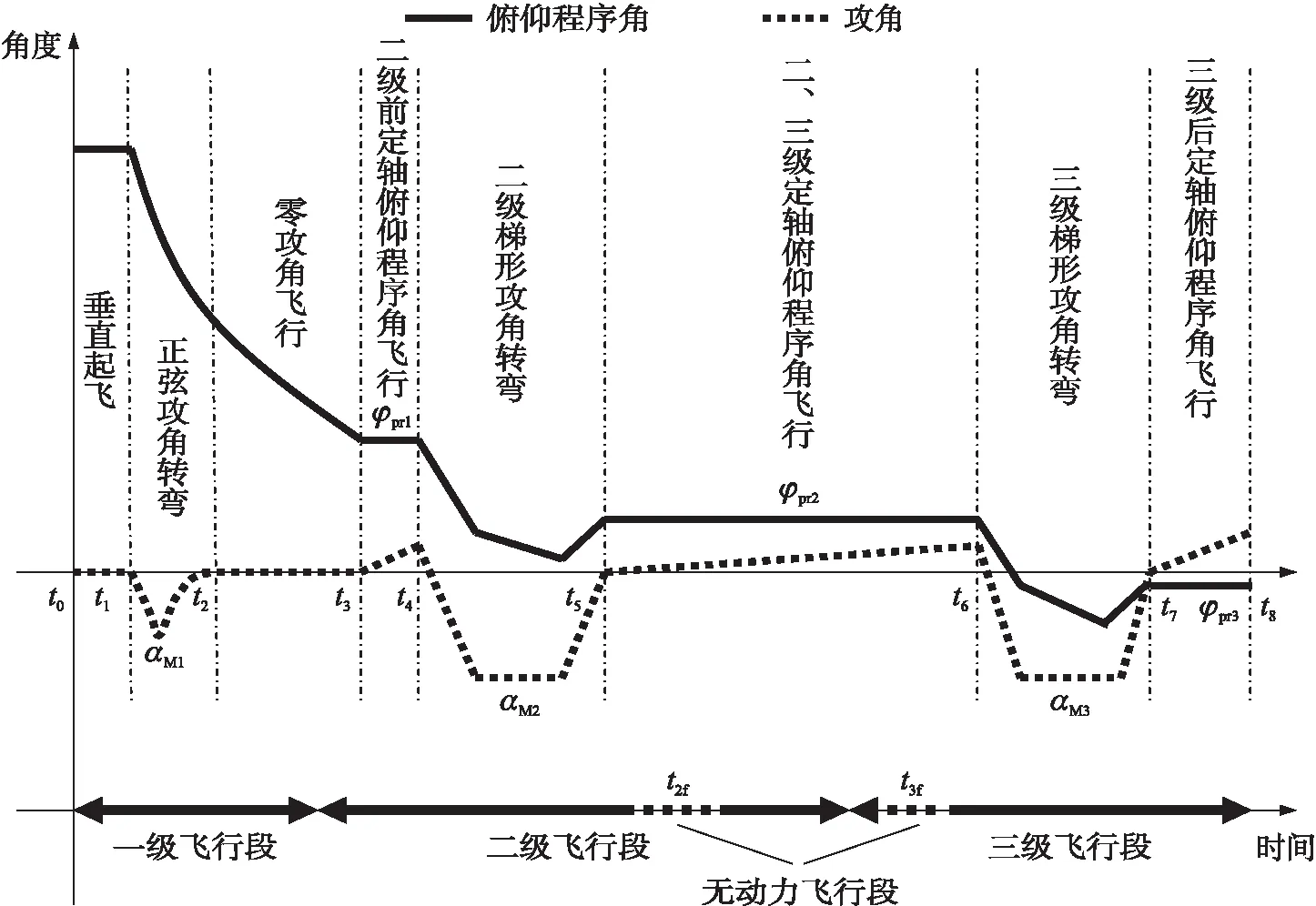
图1 飞行程序角设计示意图

图1中各段俯仰飞行程序角表达式为

(1)

式中:为速度倾角;为俯仰程序角;(),(),()分别为一级、二级、三级攻角转弯段攻角随时间变化的函数。

固体运载器的程序角设计方法如下:

①垂直起飞段。三级固体运载器为垂直发射,在进入攻角转弯时,需要一段时间进行垂直飞行。

②正弦攻角转弯段。三级固体运载器在一级发动机额定工作段开始攻角转弯,这一时间不能太早,保证发动机工作在额定状态下,转弯具有足够的控制力;同时,这一时间不能太晚,否则转弯具有较大阻力,损失运载器能量。一级要穿越稠密大气,故需要在亚音速阶段完成攻角转弯。此段采用正弦函数攻角构造法进行转弯。

③零攻角飞行段。在一级跨音速及二级飞行段初始段,飞行高度低,大气稠密,为减小大气阻力,运载器以零攻角飞行,飞行结束时刻点可根据飞行至某一高度确定。

④二级前定轴俯仰程序角段。在二级飞行段高度较高时,可实行定轴俯仰程序角飞行,对于抛头罩等分离时序的实现具有积极意义。

⑤二级梯形攻角转弯段。在二级以梯形攻角形式进行转弯,减小运载器飞行的当地弹道倾角。由于转弯时机早,二级相对于三级转弯效率高,但同时将消耗较多能量。

⑥二级、三级定轴俯仰程序角段。在二级攻角转弯后、三级攻角转弯前,均实行定轴俯仰程序角飞行,其中包含三级发动机点火前的无动力飞行段。采用定轴飞行形式对于二三级分离具有积极意义。

⑦三级梯形攻角转弯段。在三级以梯形攻角形式进行转弯,进一步减小运载器飞行程序角,由于此时大气稀薄,可采用较大攻角转弯飞行。

⑧三级后定轴飞行段。在转弯结束后,以某一定值俯仰程序角助推运载器入轨。

2 优化模型与求解流程

对助推段飞行特点分析和飞行程序角设计后,本节建立了升力式飞行器助推段优化模型,并进行了优化流程设计。

2.1 目标函数

选取初始入轨速度最大为优化目标。定义目标函数()=-,寻找优化设计变量,使得目标函数()最小,即:

min()=-

(2)

2.2 优化变量

在进行飞行程序角设计时,各级攻角转弯最大负攻角,,作为主要的设计变量,因此可作为优化变量;,,,分别为二三级攻角转弯段起始时刻和终止时刻,其需选择在发动机额定工作时间段内,并具有一定的可调节空间,可作为优化变量;此外,两段无动力飞行的飞行时间,可作为优化变量。因此,选取,,,,,,,,作为优化变量,即:

=()

(3)

2.3 约束条件

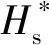
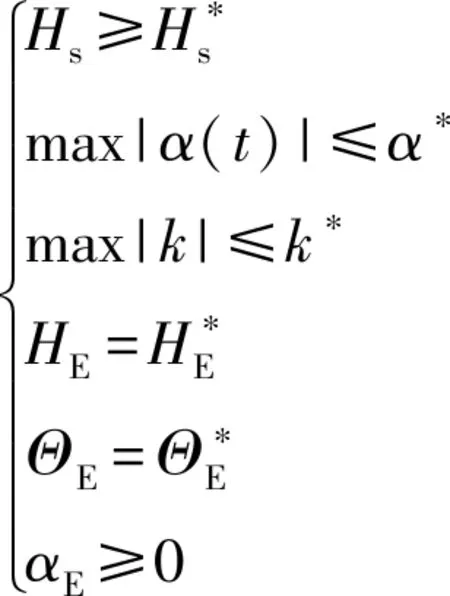
(4)

式中:为一二级分离高度,为俯仰程序角变化率,为入轨点高度,为入轨点当地弹道倾角,为入轨点攻角。

2.4 优化模型

综合以上各式,得到升力式飞行器助推段弹道优化模型如下。

目标函数:

min()=-

优化变量:

=()

约束条件:

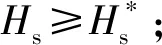
②攻角限幅约束max|()|≤;

③程序角斜率约束max||≤;

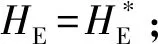
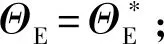
⑥入轨点攻角约束≥0。

2.5 优化流程

以牛顿迭代算法选取优化初值,并利用SQP法进行优化求解。由于自变量和约束较多,采用多轮次多维度牛顿迭代,为优化提供较为准确的初值,提高优化效率。通过深入分析模型各优化变量与约束条件的耦合关系,找出设计变量对约束的灵敏度影响,以一维或二维牛顿迭代快速找出满足部分约束的设计变量参数,从而达到降低优化设计变量维度、减少约束条件、提升优化效率的目的,优化流程如图2所示。

图2 优化流程图

3 仿真结果

针对前文给出的升力式飞行器助推段弹道设计方法、优化模型与优化流程,开展优化仿真。优化变量上下限、初值、牛顿迭代初值、优化解如表1所示,相关约束条件设定值、计算值和满足情况如表2所示。

从表1和表2中可以看出,约束条件均得到满足,优化变量值均在设计变量的优化范围内。此外,优化得到的入轨速度高出原来的3.1%,优化结果理想,进而证明了升力式飞行器助推段弹道设计方法的正确性,也验证了优化求解流程的有效性。优化后的弹道仿真结果无量纲化曲线如图3～图6所示。

表1 优化变量值

表2 约束条件设定值

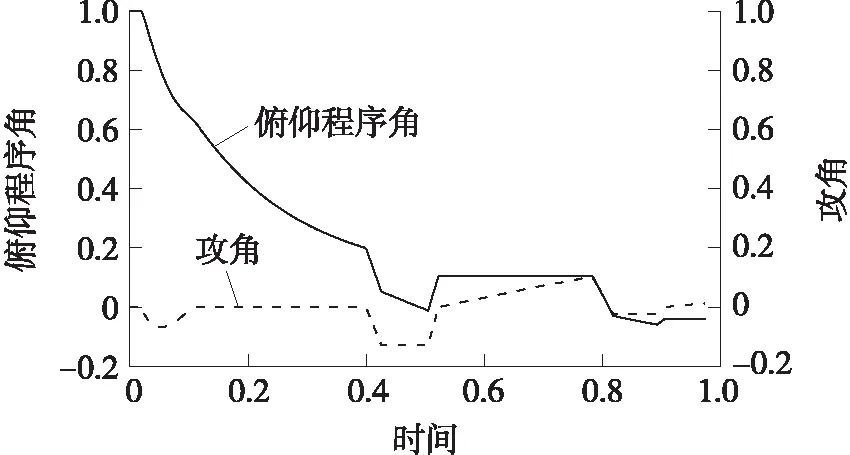
图3 攻角-时间和俯仰程序角-时间无量纲曲线

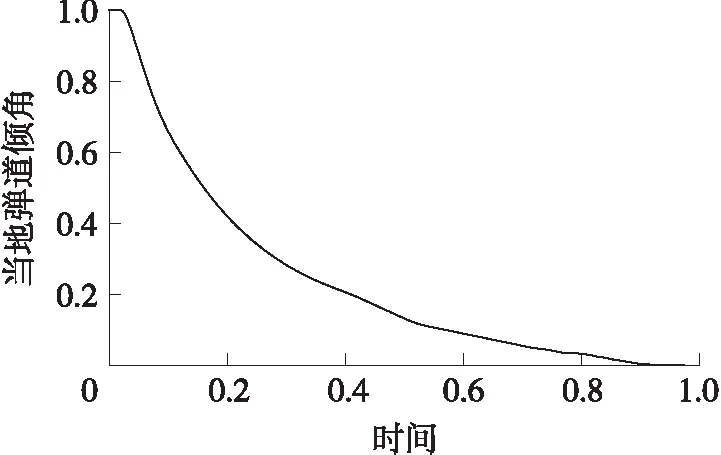
图4 当地弹道倾角-时间无量纲曲线

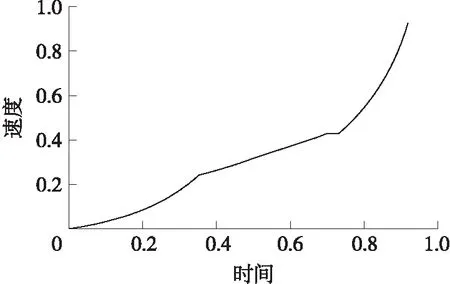
图5 速度-时间无量纲曲线

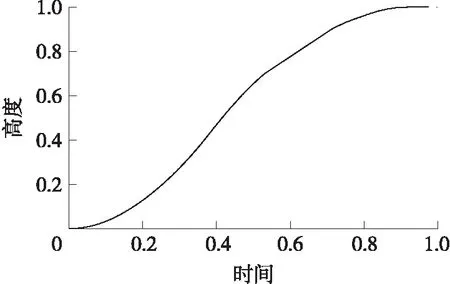
图6 高度-时间无量纲曲线

4 结束语

本文首先给出了升力式飞行器助推段弹道设计方法,选择了优化变量,确定了飞行过程约束和入轨点入轨约束,以入轨速度最大为优化目标,建立了优化模型,并以牛顿迭代法确定优化初值,且以序列二次规划法开展优化仿真。从优化结果来看,约束条件均得到满足,优化得到的入轨速度提高了3.1%,优化结果理想。本文中升力式飞行器助推段弹道设计方法具有较强的工程适用性,优化模型建立方法与优化求解流程可为其他优化问题提供参考。