板栗树振动响应特性与落果情况试验研究
2022-03-28韩元顺许林云
韩元顺,许林云,周 杰,余 兵
(南京林业大学 机械电子工程学院,江苏 南京 210037)
板栗(Blume),又称栗子、毛栗等,属壳斗科(Fagaceae)栗属()植物,原产自中国,乃中国驯化利用最早果树之一。中国是世界上板栗第一生产大国,中国板栗以优良的品质和高度的抗逆性享誉世界。截至2018年,中国板栗的收获面积已扩大至34.1万hm,产量达196.5万t。目前,中国板栗的采收主要以人工捡拾或长杆打落等方式,采收效率低下,成本较高,存在一定的作业风险,限制了中国板栗产业规模化的发展。中国板栗机械化采收是必然的发展趋势,可提高采收效率,降低劳动成本。
板栗属于干果类林果,针对此类林果最有效的采收方式是机械振动采收。国内外众多学者对于振动采收理论进行了大量的研究,Crooke等建立了三自由度果-茎振动系统,并分析了在正弦激励下该系统的动态响应情况,模拟果树在采收时动态响应;Moore等测定了9种人工栽培道格拉斯冷杉的自然频率和阻尼比,发现树木的自然频率与胸径与总树高的平方成线性相关;Castro-García等、Sola-Guirado等利用树干振动采收机械进行了对西班牙石松的振动采收,研究了落果率和对树皮的损伤,获得了最优的激振参数组合;王长勤等研究并设计了一款偏心式振动采收机,并用于核桃采收田间试验,在20 Hz的激振下采净率可达92.6%;林欢等对室内小型林果树进行加速度响应试验,分析了不同激振频率下树干、一级枝与二级枝的加速度响应情况;何苗等利用振动分离试验台进行结果枝-果蒂振动分离试验,探寻到在激振频率18.22 Hz、激振振幅7.87 mm和行进速度20.93 mm·s参数组合下采收效果最优;杜小强等利用ANSYS建立果树有限元模型,分析了三维激振下果树上各点的加速度响应;耿雷基于ANSYS和ADAMS软件对采摘机与蓝莓植株进行刚柔耦合动力学建模,分析了蓝莓振动采收机工作过程与能耗。
不同品种的果树因其生长特性与材料特性的不同,在相同的振动频率、振幅、振动时间等振动参数的激振下,具有不同的振动响应特性。目前,针对板栗树相关的振动采收理论研究非常缺乏。本文通过对板栗树进行频率特性与振动响应的田间试验,分析激振频率与落果之间的相互关系,以确定板栗振动采收的最佳采收参数。
1 材料与方法
1.1 试验地点与材料
本文田间试验地点位于江苏省南京市江宁区横溪街道官长社区西韩村板栗种植田(31°41′25″N,118°47′6″E),试验时间为2019年9月下旬,正值板栗果实采摘期的初期阶段。板栗田由栗农管理,水肥良好,无套种植物,选取其中3棵树龄为10~15 a的板栗树作为试验对象,命名为树Ⅰ、树Ⅱ和树Ⅲ,并将反映各棵树生长态势的基本特征参数进行测试并列入表1中,其中根部直径为接近地面处的树干直径,主干高为出现第一个分枝的分叉点至地面的距离,激振位置约为2/3主干高处。

表1 板栗树基本特征参数Table 1 Basic characteristic parameters of sample tree
本文主要研究板栗果树各位置点的振动响应,因此需在果树上进行测点布置。主干上布置一个测点,为激振位置上方100 mm处,各果枝上基本按果枝长度均匀布置测点,具体测点分布及各测点标号如图1-d、e、f所示,对应各测点位置处的枝干直径及各测点沿所在果枝生长方向距各果枝分叉点距离,其中树干测点T为距地面的距离,具体数值列于表2中。
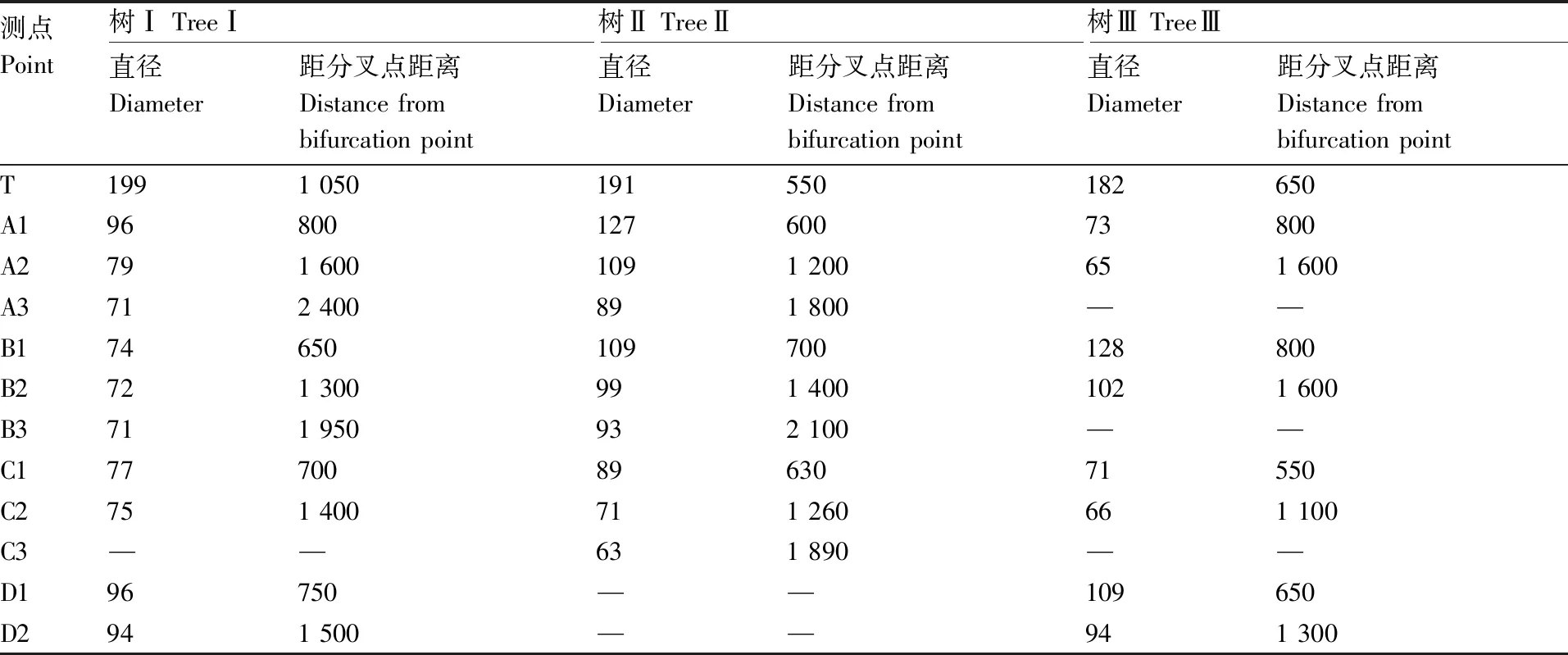
表2 各测点位置处参数Table 2 Parameters at position of each measuring point mm
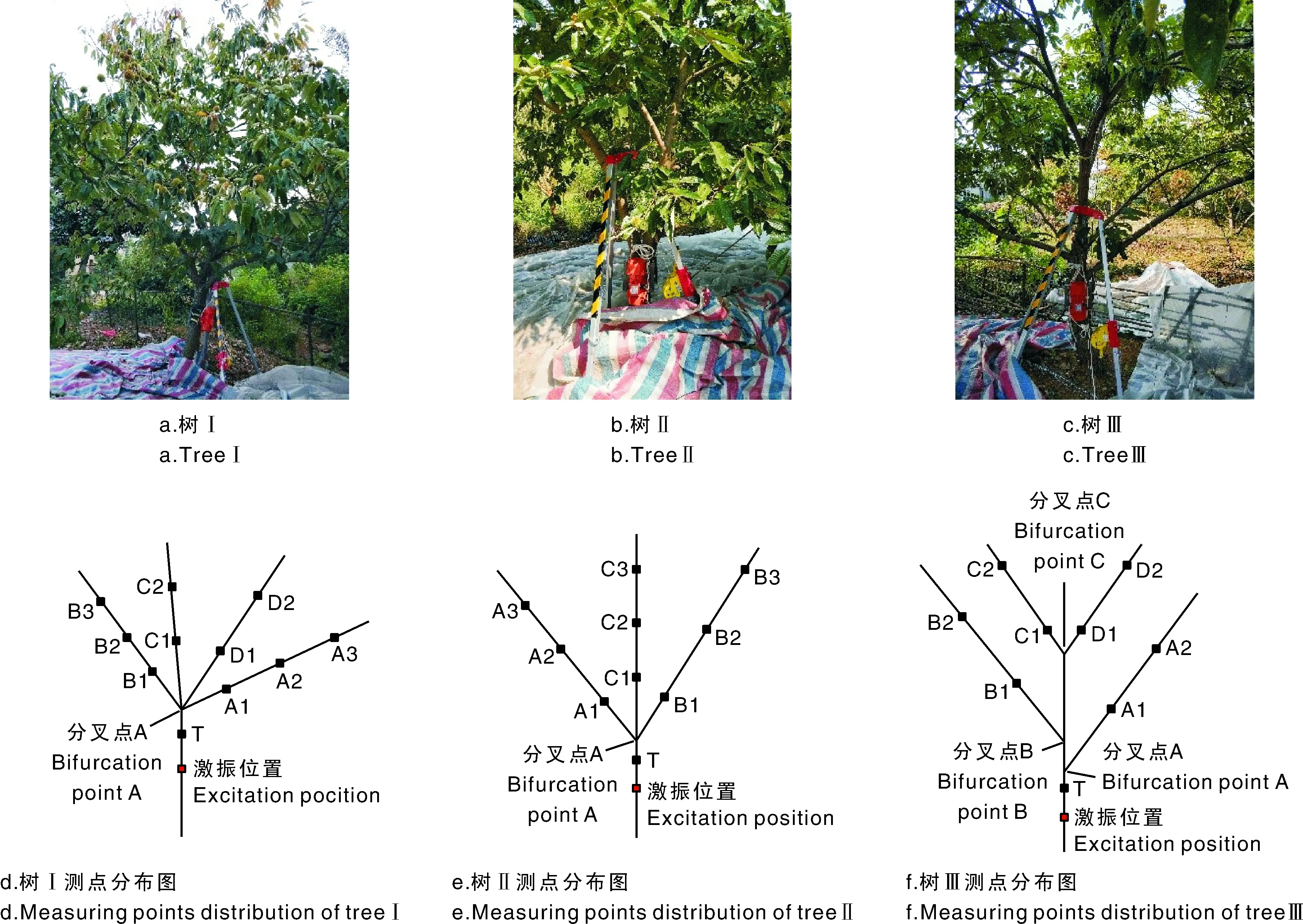
图1 板栗树与测点布置示意图Fig.1 Arrangement of measuring points
1.2 试验设备与方法
板栗振动响应及落果试验,需构建激振装置和加速度测试装置。激振装置采用单偏心激振电机(PUTA MVE500/3;Flrce:5 kN;Speed:3 000 r·min;Power:0.37 kw;Weight:15.8 kg),将其固定夹持在树干上,通过变频器(INVERTER)调节激振电机转速实现对果树的调频激振。加速度测试装置采用三向加速度传感器(1A313E),各测点可同时获取空间正交三向的3个加速度信号,应用DHDAS动态信号采集分析软件及多通道动态信号测试分析系统(DH5922D)对各信号进行采集与数据处理。
一般应用偏心块激振方式对果树适宜的采收工作频率区间主要为15~25 Hz,本试验研究设定激振频率范围为10~30 Hz,间隔为2 Hz,激振时间为10 s。由于板栗果实带有毛刺,考虑到果实的掉落对于大型果树振动响应特性的影响较小,为避免对试验人员与试验设备造成伤害,先进行落果试验,并统计每组激振频率下掉落果实数量。再进行振动响应试验,设定激振电机旋转中心与树干中心连成的水平线方向为方向,水平面内垂直于的为方向,垂直向上的树干生长方向为Z方向。三向加速度传感器在各测点的、、三向安装方向与设定方向一致,用热熔胶将其黏贴固定在各测点位置处。因加速度测试系统只有12个通道,每个测点测3个方向,因此每次试验只能同时测4个测点,需经过多次移动加速度传感器至不同测点才能完成一组设定参数下的全部试验,每组试验重复3次。
1.3 加速度幅值获取方法
利用变频器启动单偏心式激振电机会存在一定时间的响应过程,然后才会进入稳态响应阶段。如图2为在26 Hz频率激振下树Ⅱ测点B2处向加速度响应曲线,从激振开始瞬态响应持续约1 s后才能进入稳态响应阶段,随机取稳态响应阶段的连续10个峰值,取其平均值作为相应频率下对应测点处、、三个方向的加速度幅值,并按式(1)计算合加速度幅值。
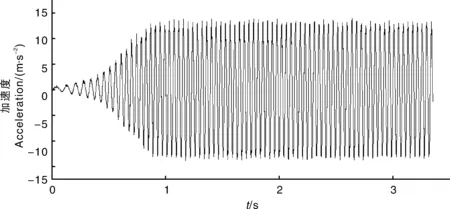
图2 在26 Hz频率振动激励下树ⅡB2测点处Z向加速度响应曲线Fig.2 Z-direction acceleration response curve of chestnut treeⅡB2 point under vibration of 26 Hz frequency
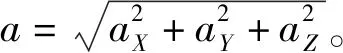
(1)
2 板栗树振动与响应理论分析
2.1 单偏心式激振装置-板栗树动力学模型
单偏心式激振装置夹持在板栗树干上,可将激振装置与板栗果树构成为一个系统,构建如图3所示的动力学模型,单偏心式激振装置可产生两个方向的激振力和,对单偏心式激振装置-板栗树动力学模型进行受力分析,可建立系统振动微分方程组:

(2)
式(2)中:为单偏心式振动激振装置-板栗树树系统的总质量,kg;和分别为板栗树沿向和向偏离原点的位,m。
根据振动力学理论,可求出单偏心式激振装置-板栗树系统在、方向的加速度响应幅值与相位差在数值上相等,并可写成相同形式:

(3)

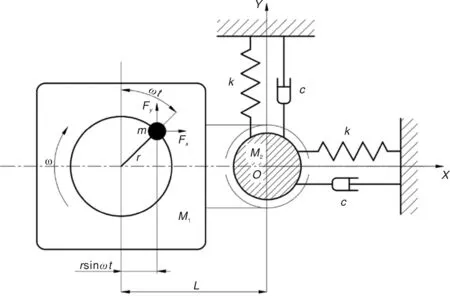
M1,偏心电机的质量(除偏心块);M2,板栗树在夹持点处的等效质量;m,偏心块质量,kg;ω,偏心块的转动频率,r·s-1;r,偏心块的偏心距,m;k,等效弹性系数,N·m-1;c,等效阻尼系数,Ns·m-1;L,激振装置转轴距板栗树中心的距离,m。M1,The mass of eccentric motor (except eccentric block);M2,The equivalent mass of chestnut tree at the clamping point;m,The mass of eccentric block,kg;ω,The rotation frequency of eccentric block,r·s-1;r,The eccentricity of the eccentric block,m;k,The equivalent elastic coefficient,N·m-1;c,The equivalent damping coefficient,Ns·m-1;L,The distance between the rotating shaft of the excitation device and the center of chestnut tree,m.图3 单偏心式激振装置-板栗树动力学模型Fig.3 Dynamic model of vibration harvester-chestnut tree

(4)
即与向的分加速度幅值与激振频率之间呈二次曲线增长关系。
实际上,单偏心式激振装置与板栗树构成的振动系统在树干上引起与向的振动位移为微小位移,对应的向位移几乎为0,则向的加速度幅值也可近似为0,可得出合加速度表达式

(5)
即理论上,树干上各点的合加速度同样与激振频率呈二次曲线增长关系。
2.2 板栗果实振动脱落条件
果树在树干上施加一定频率的激振力()作用下,如图4-a所示,将振动能量沿果枝传递至果实处,激发起果实振动响应,使果实获得加速度,果实受到重力、果柄拉力以及惯性力作用。其中惯性力可分解为法向惯性力和切向惯性力,前者产生沿果柄方向的轴向拉力,后者对果柄与果枝的悬挂点产生力矩,使果柄弯曲,如图4-b。
法向惯性力与切向惯性力可表示为
=;
(6)
=。
(7)
式(6)、(7)中为果实质量。
在实际的振动采收中,果实脱落主要依靠自身惯性力与重力的作用,当惯性力与重力沿果柄方向合力大于果实与果柄之间分离力时,板栗果实发生脱落,即
+cos>。
(8)
代入式(6),表达式则为
+cos>。
(9)
式(9)中为重力加速度,取9.8 m·s。
式(9)为板栗果实理论脱落条件。板栗果柄短而粗,可将板栗果实在稳定状态下的运动简化为随果枝的摆动,则果实所获得的加速度近似为果实悬挂点处果枝的合加速度,则悬挂点处果枝合加速度越大,果实越容易脱落。同时,研究究表明不同生长时期的果实与果柄分离力不同,随着果实成熟度的增加,果实与果柄间的分离力越小,果实也越容易脱落。但在实际振动过程中由于果树形态各异、外界干扰因素较多,还需对板栗树进行实际的测试,才能够寻找出较为合适的激振频率进行选择性采收。
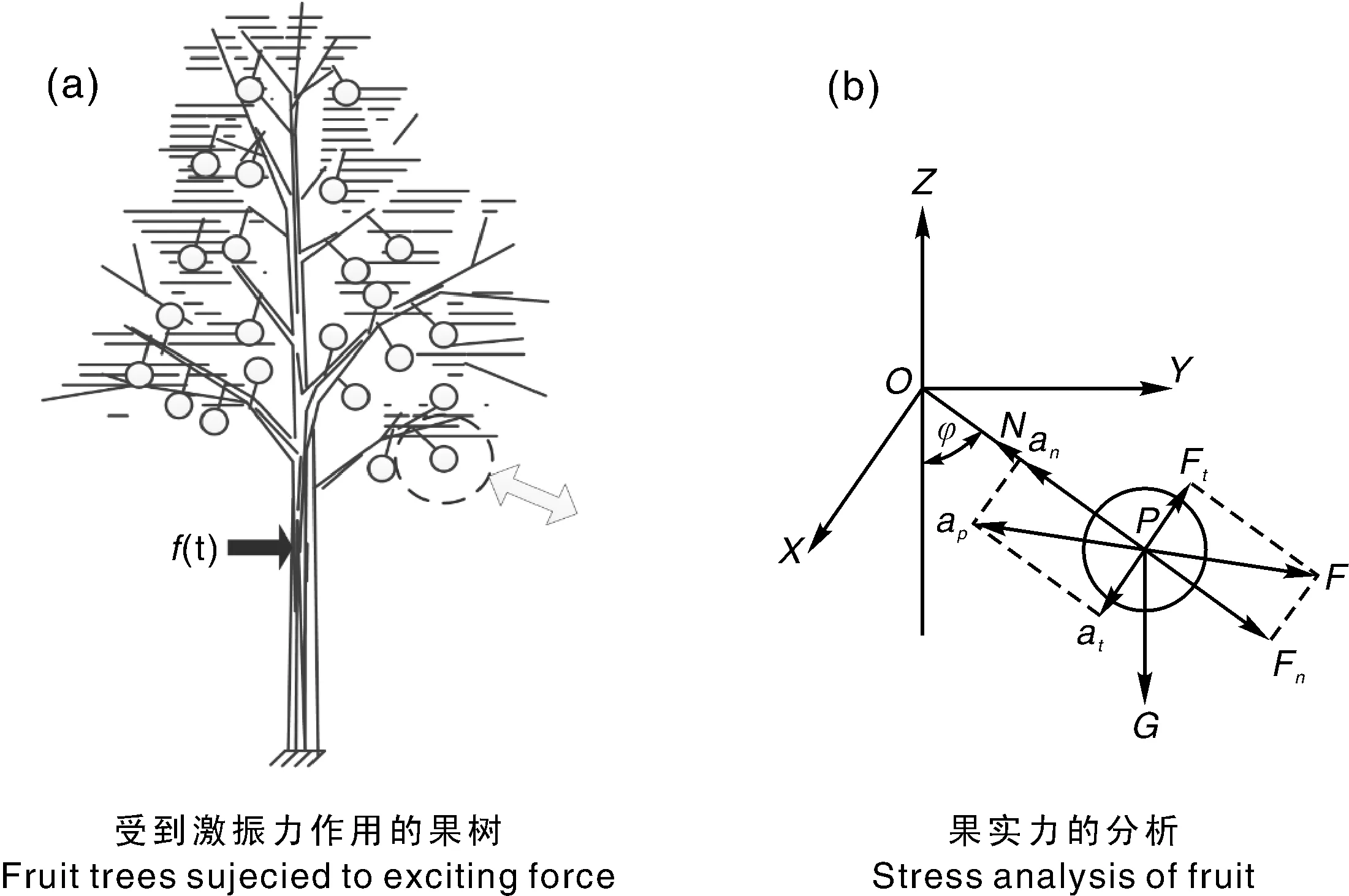
P,果实的质心;f(t),激振力;N,果实与果柄之间的分离力;F,惯性力;Fn,法向惯性力;Ft,切向惯性力;G,果实自身所受重力;N,φ为果枝与垂直方向夹角;α,法向惯性力与垂直方向夹角,°;ap,果实加速度;an,果实法向加速度;at,果实切向加速度,m·s-2。P,The center of mass of fruit;f(t),The excitation force;N,The separation force between the fruit and the stalk;F,The inertia force;Fn,The normal inertia force;Ft,The tangential inertia force;G,The gravity of the fruit itself,N;φ,The angle between the fruit branch and the vertical direction;α,The angle between the normal inertia force and the vertical direction,°;ap,The fruit acceleration;an,The fruit normal acceleration;at,The fruit tangential acceleration,m·s-2.图4 激振果树引起的果实受力分析图Fig.4 Stress analysis of fruit induced by excitation
3 结果与分析
3.1 主干加速度响应分析
三棵板栗树主干测点T的各分加速度与合加速度幅值见表3。任一棵树T点、、向的加速度幅值及合加速度均随激振频率的增加而增大,且与向加速度幅值均明显大于向的加速度幅值,这与21节理论模型分析结果一致。基于21节的理论分析,主干上各点的响应=,实际上,树Ⅰ对应于各激振频率基本上与相当,且激振频率对响应加速度的影响较明显,频率为30 Hz时达到25.07 m·s;对于树Ⅱ,当激振频率≤22 Hz时,虽然与相差不大,但响应值均较小,当激振频率为22 Hz时,略大于,只有4.58 m·s,随着频率进一步增加,值明显增加,但增加较缓慢,直至最大频率30 Hz时,=7.07 m·s,而=15.5 m·s虽远高于值,但仍远低于树Ⅰ的响应效果;对于树Ⅲ,在所有激振频率点上,均明显大于值,且频率越大,两者差值越大,当频率处于最高30 Hz时,达到最大值27.73 m·s,为的2.35倍。考虑到果树的生长形态与激振位置点,树Ⅰ的主干最高,激振位置约为树Ⅱ与树Ⅲ的2倍高度处,树干上的响应结果应与偏心式激振装置夹持点的位置有关,夹持点较低,树干中心响应轨迹易形成椭圆形式,且椭圆长轴为水平面内垂直于偏心激振电机中心与树干中心连线的方向,夹持点越高,树干中心的响应轨迹越近似于圆,这与散鋆龙等研究树干中心的响应轨迹相一致。当然,每棵树具有各自独立的生长态势,形成各自不同的树干高度、冠幅宽度、树冠质量分布等特征参数,因此该规律并不一定明显适合于所有果树。

表3 主干加速度幅值Table 3 Amplitude of trunk acceleration m·s-2
固定截距为0,利用SPSS 20.0软件对三棵树树干、向加速度幅值以及合加速度与激振频率之间关系进行拟合。
树Ⅰ、向加速度幅值及合加速度与激振频率的拟合关系为
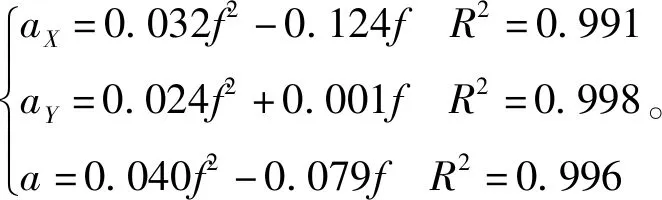
(10)
树Ⅱ、向加速度幅值及合加速度与激振频率的拟合关系为
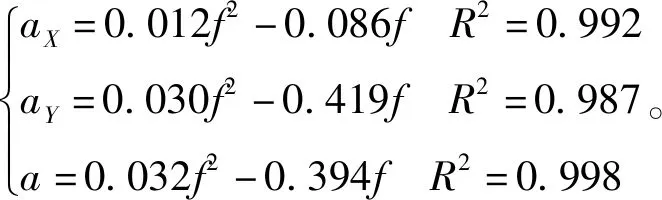
(11)
树Ⅲ、向加速度幅值及合加速度与激振频率的拟合关系为
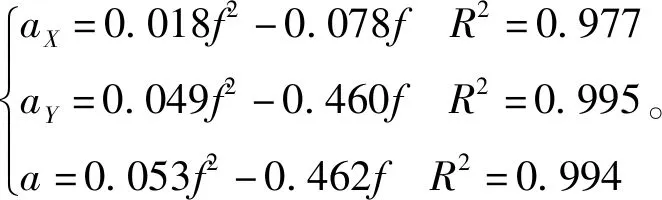
(12)
用于拟合优度检验的决定系数最小为0.977,拟合程度很高,进一步说明单偏心式激振电机激振树干时,实际所引起的加速度响应与激振频率之间的变化趋势较为符合理论推导所得的关系,都呈现出二次曲线增长的关系,增加激振频率可有效提高果树树干处振动响应。
3.2 果枝加速度响应分析
3.2.1 不同测点分加速度的差异性分析
以一定频率激振树干,振动能量的传递和分布与果树的结构密切相关,且果树分枝的运动响应在一定程度上是相对独立的,受分枝形态与尺寸的影响,在外力激励下的各分枝上的振动往往分布不均匀,这意味着即使在同一分枝上不同测点位置处的振动响应也存在一定的差异性。图5-a与图5-b为树Ⅰ同一分枝A上两个测点A1与A3在不同频率激振下的三向加速度响应幅值变化曲线,A1点向加速度幅值明显大于、向加速度幅值,且与向加速度幅值随频率呈现交错上升变化关系,而A3点以向加速度幅值最大,且与向加速度幅值随频率呈现不同的变化趋势关系。因位于各测点的果实获得的惯性分离力主要与该测点的合加速度有关,非必须区别各方向的分加速度幅值,因此以下各测点不再区分三向分加速度,而以合加速度幅值代表该测点的振动响应。
3.2.2 谐响应效果分析
果树存在许多谐振频率,同一果树的不同部位存在某些相同的谐振频率,同时又因各果枝具有各自独立的振动特性,相互之间又存在许多不同的谐振频率。理论上,当激励频率达到或接近某测点的固有频率时此测点则会发生明显的谐振响应现象。在激振板栗果树与各测点加速度响应试验过程中发现,果树存在相当多的谐振频率,但并不是所有的谐振频率都能激发起明显的或强烈的谐振响应,即使在某些谐振频率能引起一定的谐振响应,也不是在所有方向上均能获得明显较大的加速度幅值。如图6-a,树Ⅰ测点A2对应、向加速度幅值曲线在18~24 Hz各呈现出一个峰包现象,而在较高的24 Hz时出现谷底,但对于向的加速度响应则没有出现峰包和谷底现象,而是随频率连续增长,从而对于合加速度曲线则削弱了分加速度曲线的波动深度,达到平滑曲线的效果,因此,合加速度曲线总体呈现随频率增长趋势关系;图6-b所示的树Ⅲ测点A1的加速度幅值与频率曲线关系,22 Hz时、方向的加速度幅值出现明显的共振峰现象,且在整个频率范围内均为最大值,虽然向未显示出共振现象,但因该频率点与向的共振响应现象特别显著,致使合加速度曲线也在22 Hz处形成共振峰,但这种现象特别少。
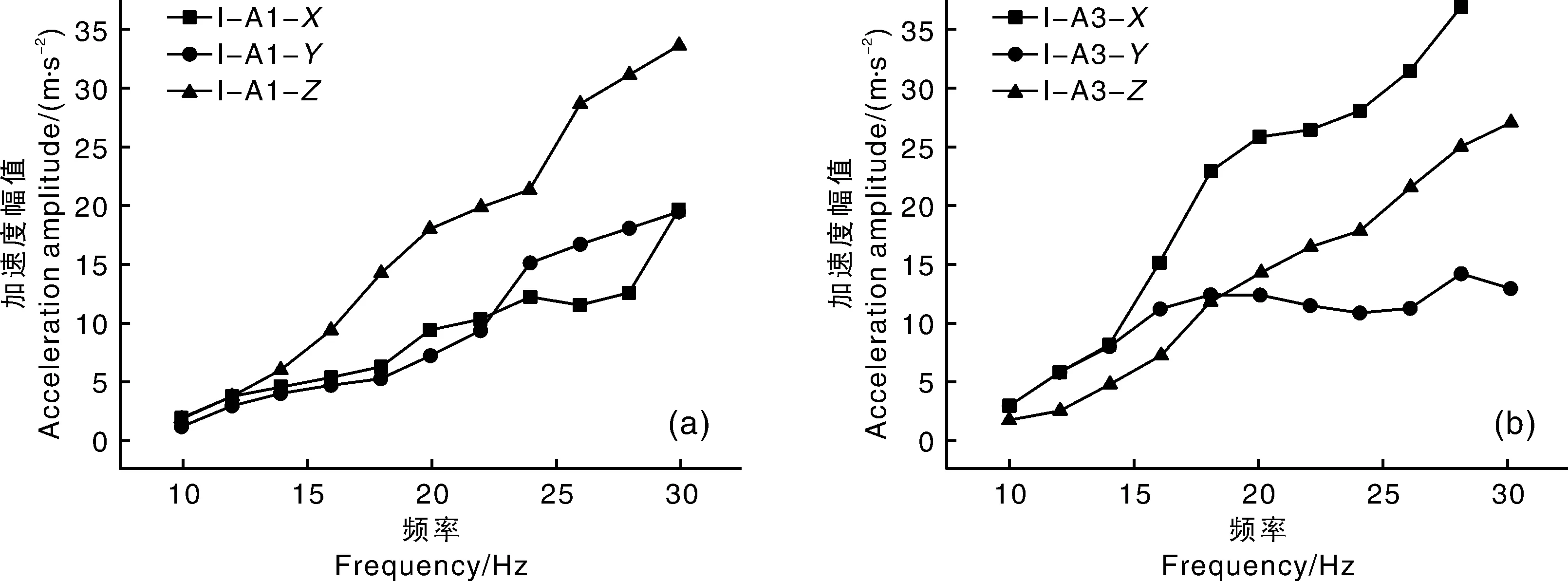
a,树Ⅰ测点A1;b,树Ⅰ测点A3。a,Sample tree Ⅰ point A1;b,Sample tree Ⅰ point A3.图5 树Ⅰ测点A1与A3处三向加速度幅值变化曲线Fig.5 Acceleration amplitude variation curves of three-direction acceleration at measuring point A1 and A3 on treeⅠ
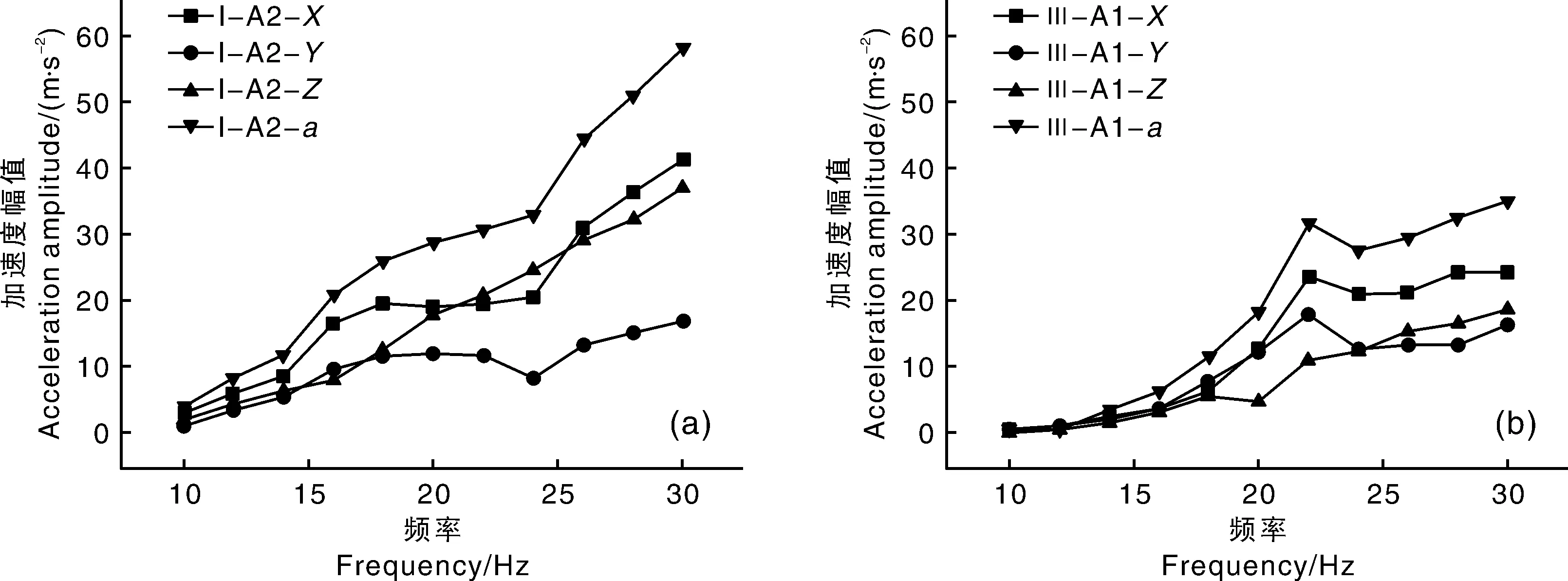
a,树Ⅰ测点A2;b,树Ⅲ测点A1。a,Sample tree Ⅰ point A2;b,Sample tree Ⅲ point A1.图6 树Ⅰ测点A2处与树Ⅲ测点A1处加速度幅值变化曲线Fig.6 Acceleration amplitude variation curves at measuring point A2 on tree Ⅰ and point A1 on tree Ⅲ
3.2.3 各测点合加速度响应分析
三棵板栗树果枝上各测点的合加速度响应幅值见表4。除树Ⅲ测点A1与A2处在22 Hz时出现极大值情况,其余各测点合加速度幅值均随激振频率的增加而增大,并于30 Hz时达到最大值。就整体而言树Ⅰ增长趋势最快,树Ⅲ次之,树Ⅱ增长趋势最为缓慢,树Ⅰ果枝上的测点合加速度幅值基本在14~16 Hz时超过10 m·s,树Ⅲ果枝上的基本在18 Hz时超过10 m·s,树Ⅱ果枝上的则基本在22 Hz时才超过10 m·s。当频率处于最高30 Hz时,以树Ⅰ果枝上的各测点合加速度幅值均值最大,为52.3 m·s,树Ⅲ次之,为48.8 m·s,树Ⅱ最低,为33 m·s,这与各果树树干上合加速度幅值大小顺序一致,可见果树树干振动响应越大,整体果枝的振动响应则越强烈,反之则越弱。而各测点的合加速度幅值受果枝尺寸、形态和距分叉点距离等因素影响各不相同,但除树Ⅰ的A枝、B枝与树Ⅱ的A枝外,其余各果枝上距分叉点越远的测点,其合加速度幅值则越大。
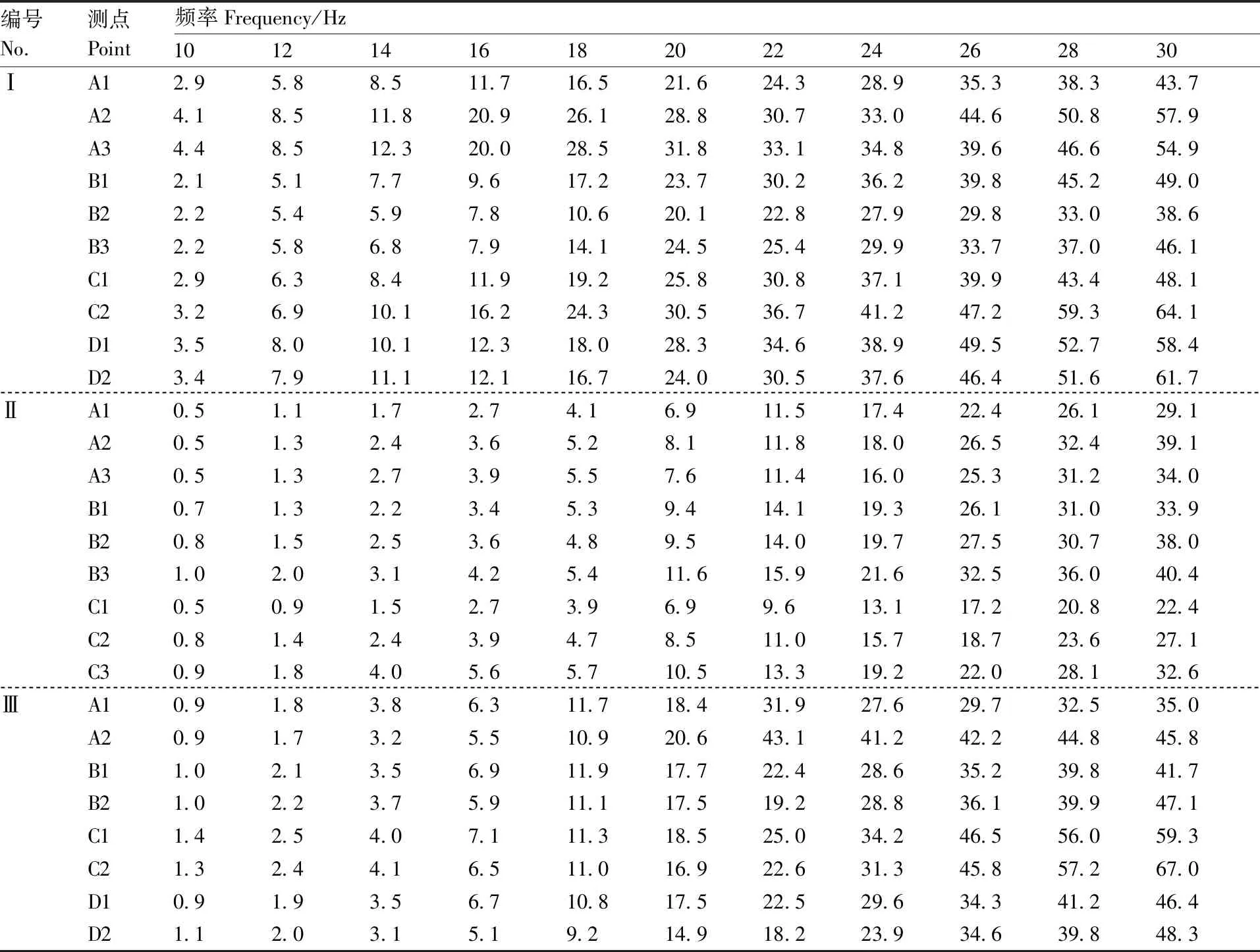
表4 果枝各测点的合加速度幅值Table 4 Combined acceleration response amplitude at measuring points of fruit branch m·s-2
各果枝上测点的合加速度幅值与激振频率之间可拟合为如式(13)所示的关系,系数及拟合优度检验的决定系数如表5所示,除树Ⅲ的A枝外,其余各果枝的拟合程度都很高,各果枝上测点的合加速度与激振频率之间仍为二次曲线增长关系,这与林欢等、崔文哲等的研究结果较为一致。
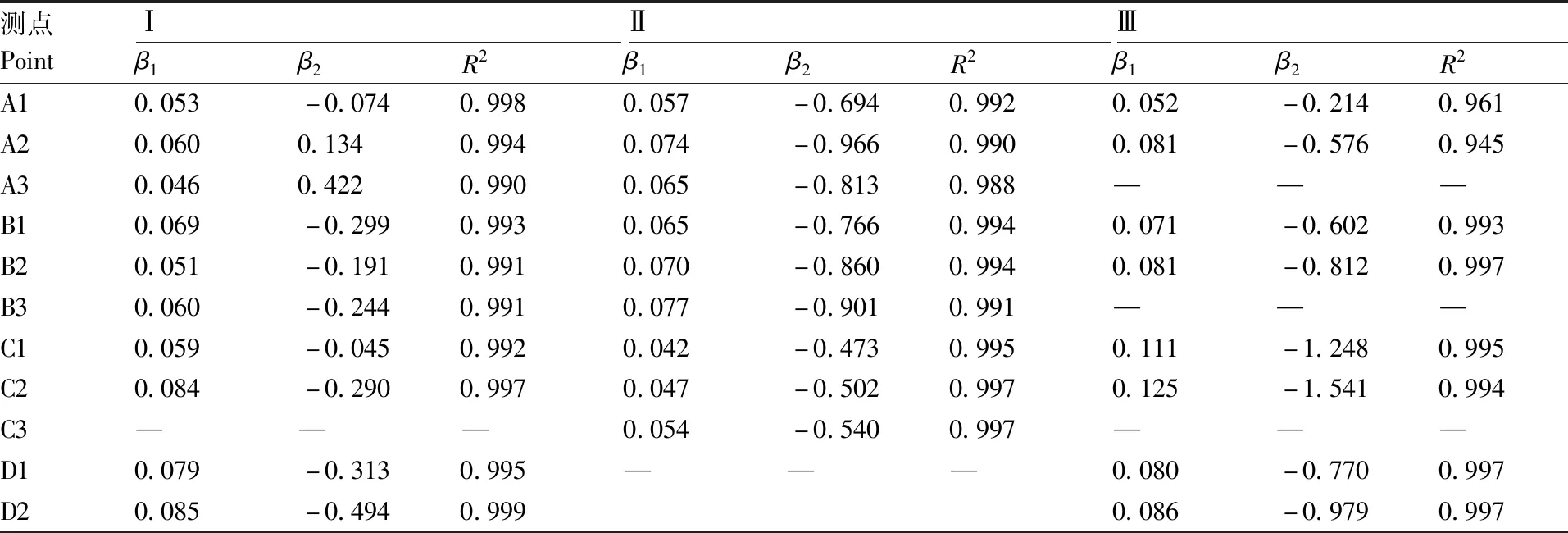
表5 拟合系数与决定系数Table 5 Fitting coefficient and determination coefficient
=+。
(13)
综上,三棵板栗树果枝上各测点合加速度幅值基本随着激振频率的增加呈现二次曲线增长的趋势,且在30 Hz的频率激振下达到最大值,激振频率的增加有利于板栗树各分枝振动响应的增强,进而提高果实所获得的惯性力,增加果实脱落几率,从而提高果实的采净率,但过高的激振频率可能会降低所采收果实的品质,为确定合适的激振频率,还需对实际落果情况进行分析。
3.3 落果情况分析
板栗果实随成熟度的增加,其栗苞会逐渐张开,完全成熟时,栗子会自栗苞中掉落,仅在树上留下空栗苞,如图7,如若不能及时捡拾,则会因腐烂、虫蛀等造成一定的经济损失。为了降低损失和提高所采收板栗果实的品质,果农一般采用分批次打落的人工采摘方式,将树上已成熟的板栗果实用竹竿一次性打落下来,未成熟果实则保留在树上继续生长,等待成熟后再进行采收。根据调查,果农一般依据板栗栗苞开口程度、栗苞颜色与栗壳颜色对板栗成熟度进行判断,依据此经验本文将所振落的果实进行了成熟度划分,认为当栗苞有一定的开口且颜色呈微黄色,栗壳基本呈棕色时,板栗果实达到可采收的成熟果实的标准。

1,空栗苞;2,成熟果实;3,未成熟果实。1,Empty chestnut bud;2,Mature fruit;3,Immature fruit.图7 板栗果实实物图Fig.7 Physical picture of chestnut fruit
将振动采收下来的果实收集,并依据上述判断标准对板栗成熟与否进行区分。由于部分成熟果振落下来存在栗苞与栗子分离的情况(图8),本试验所选板栗树栗苞中栗子含量基本为3颗,以3颗栗子作为一个成熟果实计入成熟果落果数当中。统计各频率激振下成熟果与未成熟果落果数量,同时依据各果枝合加速度随频率增加而逐渐增大的规律,加之果实在低频下很难掉落或掉落极少,在高频下会有大量果实掉落,故可认为在低频激振下掉落的果实同样会在高频下掉落,对各频率下成熟果与未成熟果实落果数量进行累加,并计算其落果率:

图8 振落下栗子与栗苞分离的果实Fig.8 Shaking down the chestnut fruit separated from the chestnut bud
成熟果落果率计算公式:

(14)
未熟果落果率计算公式:
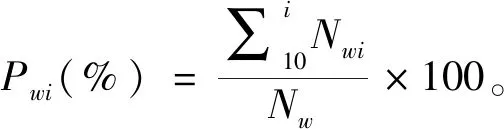
(15)
式(14)、(15)中:,频率的成熟果落果数,个;为频率的未成熟果落果数,个;为频率的成熟果整果脱落数,个;为成熟果实总数,个;为未成熟果实总数,个;为频率的成熟果落果率,%;为频率的未成熟果落果率,%。
试验前,人工对每棵板栗树上的板栗果实总数进行统计。3棵树上板栗果实总数各不相同,其中以树Ⅰ最多,约550个,其中成熟果实约200个;第二棵树次之,约400个,其中成熟果实约170个;第三棵树果实最少,约350个,其中成熟果实约130个。不同频率下3棵树落果情况统计结果如图9所示。
三棵果树在10~30 Hz激振频率下果实脱落数量、变化趋势各不相同。在10~12 Hz的低频激振下,三棵树上仅有少量果实脱落甚至没有果实脱落,且脱落下的果实都为成熟果,直到16 Hz时,三棵树上都开始有未成熟果实脱落,其中树Ⅰ的未成熟果脱落最多,达25个。树Ⅰ在16 Hz、20 Hz频率激振下果实脱落总数较多,分别为40个与50个,具有明显的峰值变化,此时亦是成熟果落果数的最多的两个频率;在频率22~30 Hz时,果实脱落总数呈轻微下降趋势,成熟果落果数基本呈下降趋势,而未成熟果实脱落数量则呈上升趋势。树Ⅱ上果实脱落总数在10~20 Hz呈上升趋势,且在20 Hz时达到峰值,此时成熟果落果数最多,达28个;在22~30 Hz频率下果实脱落总数基本持平,但成熟果落果数也有所下降。树Ⅲ果实脱落数量波动较大,18 Hz时果实脱落总数与成熟果落果数都较大,出现峰值变化,在24 Hz时果实脱落总数也较多,此时成熟果与未成熟果落果数仅相差2个。
对各频率的成熟果与未成熟果落果数进行累加并计算落果率,为了明确成熟果与未成熟果落果率随频率变化的规律,利用SPSS 20.0软件对落果率变化曲线进行拟合分析,拟合曲线如图10,三棵树成熟果落果率随频率变化呈现出三次曲线增长关系,而未成熟果落果率随频率则呈二次曲线增长关系。因在低频下果枝振动响应较小,此时两种成熟度的果实落果率均较低;随着激振频率的增加,果枝振动响应随之增大,成熟果与未成熟果落果率的增长趋势都愈加明显;而在26 Hz后成熟果落果率增长趋势都趋于平缓,这是由于果树上未掉落的成熟果实越来越少,即使再增大激振频率,成熟果实也落无可落,未成熟果落果率仍快速增长。
激振频率为30 Hz时,三棵树的成熟果和未成熟果总落果率如表6所示。三棵板栗树成熟果总落果率均值约80%,未成熟果总落果率均值也达到了32.4%。其中,树Ⅰ成熟果落果率最高,达到85%,树Ⅱ成熟果落果率最低,为74.1%,其未成熟果落果率也最高,达37.8%。
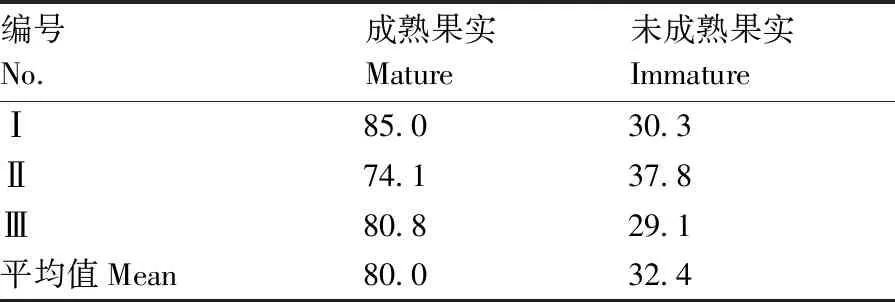
表6 落果率统计Table 6 Fruit dropping rate statistics %
由此可知,在10~30 Hz激振下,大量成熟果实振落的同时伴随着较多未成熟果的振落。而依据果农分批次打落板栗成熟果实的采摘方式,选择性振动采收的方法更适合板栗果实的机械化采收,即设置合理的振动参数,分批次对板栗树进行振动采收作业,理想的情况下每次振动采收下的板栗果实都为成熟果,未成熟果实或已成熟但未能振落的果实可留在板栗树上继续生长等待下一批次的采收。
因每棵板栗树的落果情况各不相同,仅从统计数据上难以确定合适的采收频率,为确定最佳振动采收频率,本研究采用综合评分的方法对统计数据进行分析,综合考虑成熟果落果率,未成熟果落果率以及各频率下落果情况中成熟果与未成熟果所占百分比,评分标准如下:
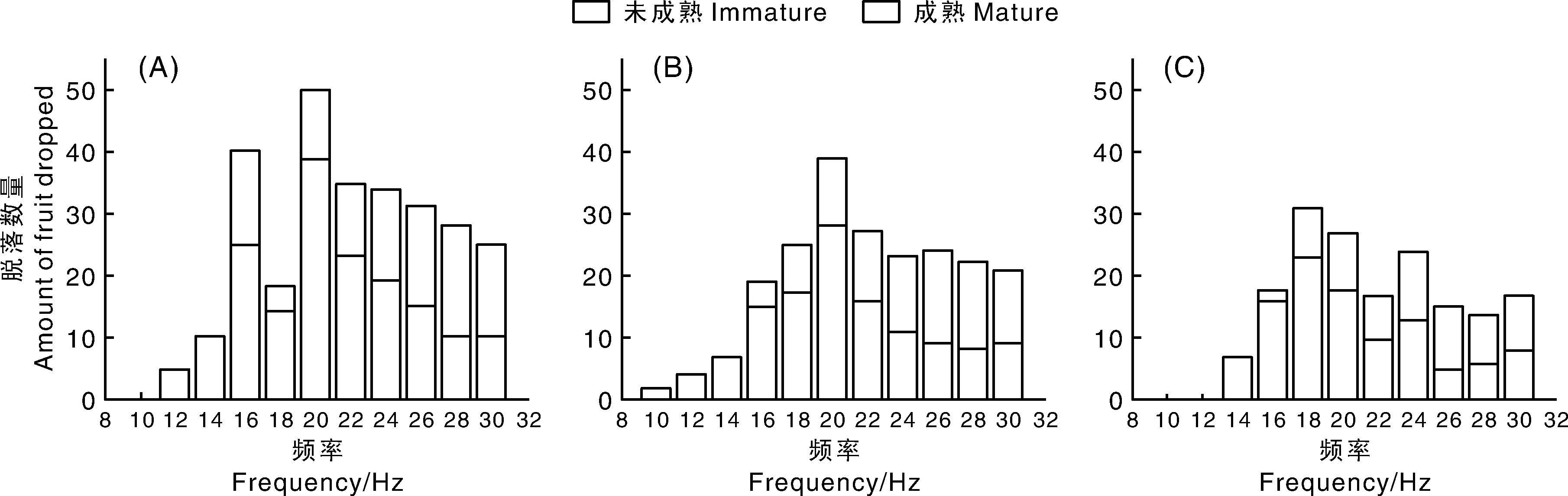
A,树Ⅰ;B,树Ⅱ;C,树Ⅲ。A,Sample tree Ⅰ;B,Sample tree Ⅱ;C,Sample tree Ⅲ.图9 不同频率下落果个数统计图Fig.9 Statistical figure of dropped fruit at different frequencies


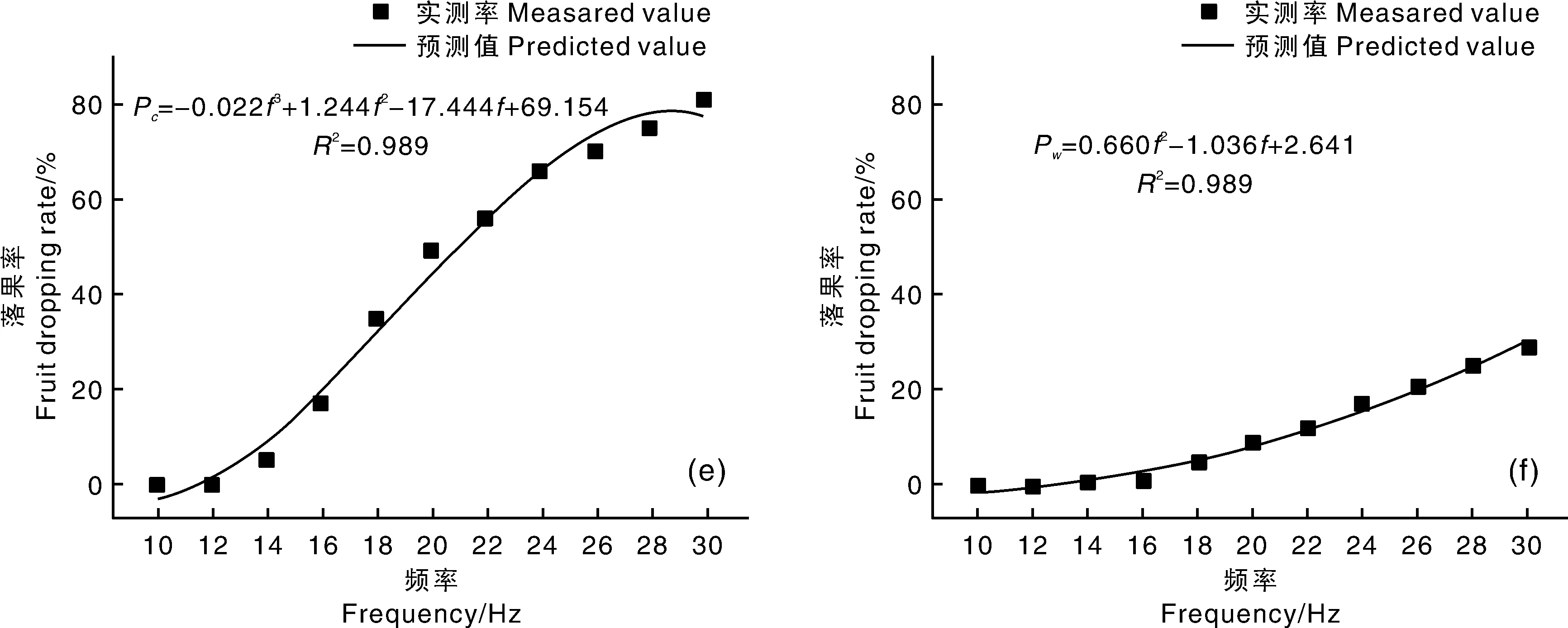
a,树Ⅰ成熟果实;b,树Ⅰ未成熟果实;c,树Ⅱ成熟果实;d,树Ⅱ未成熟果实;e,树Ⅲ成熟果实;f,树Ⅲ未成熟果实。a,Tree Ⅰ mature fruit;b,Tree Ⅰ immature ripe fruit;c,Tree Ⅱ mature fruit;d,Tree Ⅱ immature fruit;e,Tree Ⅲ mature fruit;f,Tree Ⅲ immature fruit.图10 板栗果实落果率随频率变化曲线拟合Fig.10 Curve fitting of Chinese chestnut fruit dropping rate with frequency change
1)当成熟果落果率低于10得分=0,高于90得分=100,成熟果落果率在10%~90%时得分:
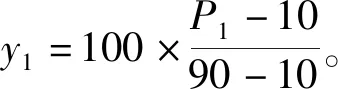
(16)
2)当未成熟果落果率低于5得分=100,高于25得分=0,成熟果落果率在5%~25%时得分:

(17)
3)各频率下脱落板栗果实成熟果数量所占此频率下果实脱落总数量的百分比为,未成熟果数量所占百分比为,各频率下落果情况得分:
=-。
(18)
4)通过调查栗农对板栗采收时成熟果与未成熟果落果率重视程度,并结合本试验实际的落果情况,分配成熟果落果率得分在总得分中占50%,未成熟果落果率占40%,各频率下落果情况得分占10%。
根据所定标准,得到综合评分,并按式(15)对评分进行归一化处理,结果如表7所示。

表7 综合评分表Table 7 Comprehensive score table
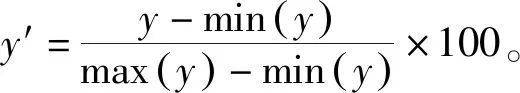
(19)
树Ⅰ在20 Hz与22 Hz,树Ⅱ在18 Hz与20 Hz,树Ⅲ在18 Hz与20 Hz下落果综合评分都大于90分,综合三棵树的综合得分情况,推荐使用18~22 Hz的频率对板栗树进行分批次的振动采收作业,可达到选择性采收的效果。
4 结论
1)对三棵板栗树树干测点处、向加速度响应曲线以及合加速度响应曲线和各果枝上的测点处合加速度响应曲线进行了拟合,发现其基本都随频率增加呈二次曲线增长关系。
2)对三棵板栗树成熟果与未成熟落果率随频率变化曲线进行拟合,发现三棵板栗树成熟果落果率随频率变化呈现出三次曲线增长关系,而未成熟果落果率随频率则呈二次曲线增长关系。
3)受果枝形态与尺寸的影响,各果枝上测点无论是三向加速度幅值亦或是合加速度幅值都存在一定差异性,但总体而言各果枝上测点的合加速度幅值都随着激振频率的增加而增大,且在30 Hz激振频率下达到最大值,这表明激振频率的增加可以使得果树各分枝获得更大的加速度响应,从而有助于提高果实采收率。
4)随着激振频率的增大,板栗成熟果实与未成熟果实的落果总量也逐渐增大。低频激振下果实落果数量较少,高频激振下果实落果数量较多,但未成熟果实落果数量也随之增大,本文用综合评分的方法对各指标进行了分析,发现三棵板栗树落果情况在18~22 Hz的激振频率下得分较高。
本文所选试验果树树龄为10~15 a,主干尺寸很相似,但抚育、管理方式粗放,导致整个冠型存在一定的差异,用综合评分的方法对进行分析后仍具有激振效果较好且相近似的激振频率区间,基于此,随着板栗树的抚育、培植、管理等技术越来越高,越来越精细化,板栗树生长形态更一致,更加可采用单一的频率对整个果园的板栗进行振动机械采收。
