主管受拉的K形圆管节点抗冲击性能试验研究

2022-03-27王庆凡

振动与冲击 2022年6期

曲慧，王庆凡，李伟，陈琦，徐洁

(1. 烟台大学土木工程学院，山东烟台 264005；2. 北京市建筑设计研究院有限公司，北京 100045)

钢管结构因其质量轻、强度高、外观美观等优点被广泛用于飞机航站楼、火车站、桥梁、海洋平台等。节点是结构的传力构件，在撞击、爆炸等突发事故中，节点可能因受到冲击荷载而破坏，严重时甚至会引起结构坍塌。因此近几年来，对管结构抗冲击性能的研究成为全球的研究热点。

目前，国内外学者采用试验研究和有限元分析相结合的方法对不同形式的管节点开展了抗冲击性能研究。如，Yu等[1]对火灾下T形圆管节点进行了抗冲击性能试验研究，得到火灾下与常温管节点的动态破坏模态均为主管与支管相贯部位的局部凹陷。Liu等[2]研究了主管直接受撞的T形圆管节点的抗冲击性能；曲慧等[3-5]以主管轴压比为参数，进行了T形圆管节点落锤冲击试验和有限元数值研究，并采用基于能量方法的塑性铰理论，较为准确地计算出在节点形成塑性铰过程中，局部凹陷和节点发生整体弯曲变形所耗散的能量，进而得到等效冲击力。Cui等[6-7]则对T形方钢管节点的抗冲击破坏机理进行了研究。王学蕾等[8-10]分别对K形管节点的冲击性能进行了研究。总体上，目前多数成果主要是针对T形管节点开展的研究，对管结构中常见的K形节点的研究较为少见；且在研究过程中，多数研究者没有考虑节点受撞前的初始应力状态，或仅考虑组成节点的主管的受力状态。

事实上，服役中的主管和支管是承受轴向的拉力或压力的，且轴向力的方向和大小将决定节点的破坏形态，以及节点局部破坏和整体破坏程度。另外，实际工程中，主管和支管的初始受力状态是不确定的，因此有必要对主管承受拉力工况下的节点进行抗冲击性能研究。

本文以节点初始受力状态和主管径厚比为试验参数，对两组6个K形圆管节点试件进行落锤冲击试验研究。通过试验研究，旨在确定不同主管径厚比、节点初始受力状态下节点的破坏模态；通过分析冲击力、节点各关键部位的冲击变形等抗冲击性能指标，揭示K形圆管节点抗冲击机理，进而验证和评价现有冲击承载力确定方法的适用性。

1 试验概况

1.1 试件设计

根据GB 50017—2017《钢结构设计标准》[11]，以典型管桁架中的K形管节点为对象，参照该类管节点工程常用参数范围，并结合落锤试验机的试验能力，设计并制作了主管径厚比不同的两组共6个K形管节点试件进行落锤冲击试验。每组3个试件的初始受力状态分别为主管及支管未施加初始轴力、主管施加轴拉力两支管施加轴压力、主管施加轴拉力两支管分别施加拉力和压力。冲击锤头与试件接触区域长度(a)为200 mm，宽度(b)为50 mm，冲击锤头质量(m)为704.4 kg，下落高度(h)为4.6 m，最大速度(v)为9.495 m/s。试件构造详图如图1所示，图1中试件由主管、两个支管以及端板组成，其中试件高度(H)为0.98 m，两支管间距(g)为50 mm，主管端板厚度(tb)为30 mm，支管端板厚度(td)为25 mm。试件几何参数以及荷载参数如表1所示。

图1 试件构造详图

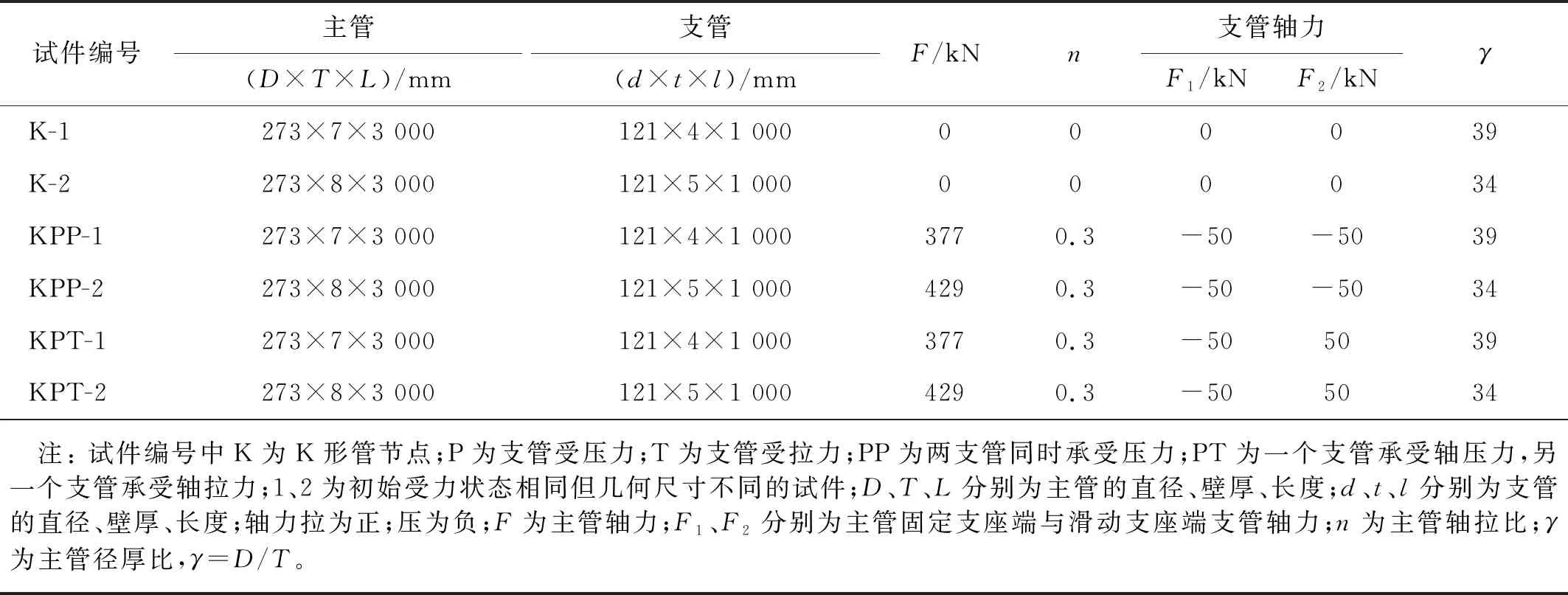
表1 试件基本参数

1.2 试件材料力学性能

试验中试件主支管均采用20号钢无缝钢管，钢管厚度为4 mm、5 mm、7 mm、8 mm，由材料力学性能的单向拉伸试验得到钢管的力学性能指标如表2所示。

表2 钢材力学性能指标

1.3 试验装置及数据测量

本试验采用的是湖南大学工程结构综合防护实验室高性能落锤冲击试验机。落锤试验机主要由控制系统、提升系统、导轨、落锤、机架等部分组成[12]。

冲击试验前，在主管和支管上分别施加轴向力。试件的边界条件为主管处一端固定，一端滑动，支管端部铰接。主管轴力通过千斤顶挤压碟形弹簧施加，以保证试验过程中预加力可以连续的加在主管上；支管压力通过千斤顶挤压支管实现，支管拉力通过拧动高强度螺栓张拉支管实现，受力简图如图2所示，冲击试验装置如图3所示。冲击荷载通过将锤头提升至指定高度再令其自由下落撞击节点来实现。

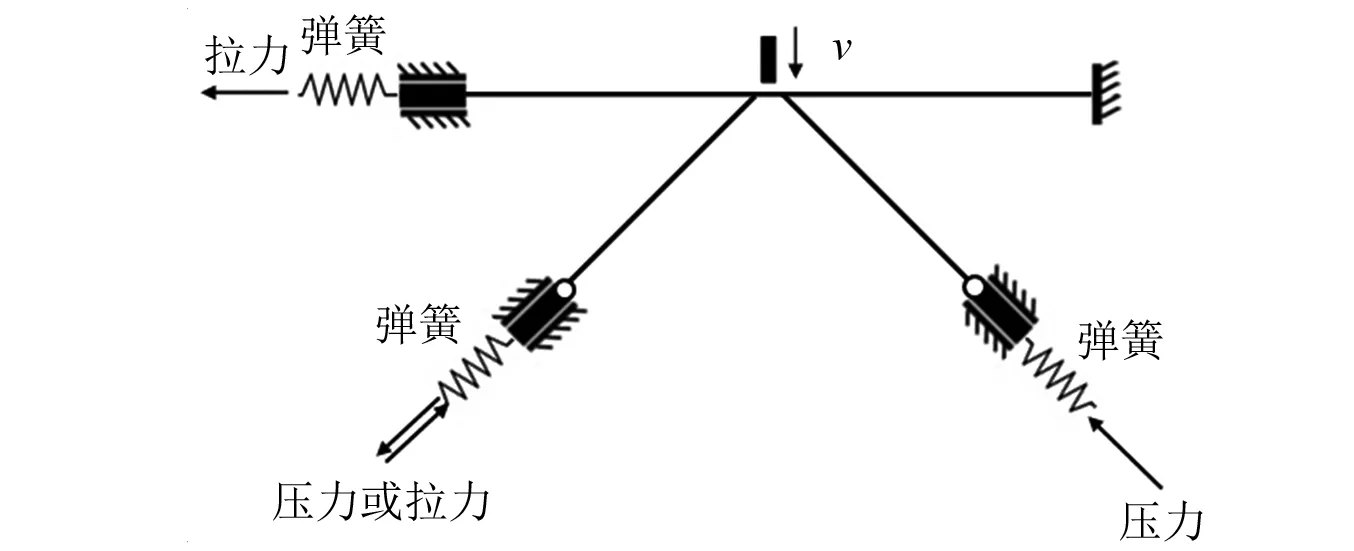
图2 试件受力简图

试验过程中，冲击力通过固定在锤头的压电传感器[13]采集到的应变换算得到。节点位移通过位移计测得，分别在节点处主管侧面、底部焊接钢板，用来连接位移计D1、D2、D3，用来测量节点侧向鼓曲、侧面竖向位移、底面竖向位移，位移计的布置如图3所示。

图3 试验装置图

2 试验结果及分析

2.1 破坏模态

受冲击荷载后的各节点的破坏模态，如图4所示。从图4可知，所有试件变形相似，即节点主管整体变形及支管变形并不明显，最终变形主要表现在主管上表面受撞击区域的局部凹陷屈曲，且主管的凹陷深度从受冲击区域向主管两端逐渐减小。支管的受力状态使得主管下表面的产生以下3种变形模式。模式一，支管不受力(试件K-1、K-2)时，主管下表面无明显变形；模式二，两个支管同时受压(试件KPP-1、KPP-2)时，两支管与主管相贯处主管下表面出现轻微的向内凹陷变形；模式三，一个支管受压另一支管受拉(试件KPT-1、KPT-2)时，因受力方向相反，两支管与主管相贯处主管下表面表现为受压凹陷和受拉外凸并存的变形模式。

图4 节点破坏模态

试验结束后将试件沿截面1-1剖开，可以看出试件主管跨中截面冲击前后变形，如图5所示，即由冲击前的圆形变为近似于半圆形。试验后主管截面的竖向高度Dv，横向宽度Dl，如表3所示。

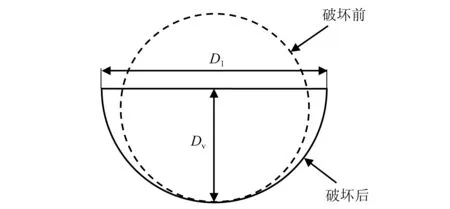
图5 主管冲击前后变形示意图

表3 试件的冲击力峰值及变形

基于图4以及表3，比较主管径厚比相同的试件(K-1、KPP-1、KPT-1或K-2、KPP-2、KPT-2)截面的残余变形可以看出，主管承受轴拉力两支管同时承受轴压力的试件(KPP-1、KPP-2)凹陷量及鼓曲量最大，其次是主管承受轴拉力两支管分别承受轴拉力和轴压力的试件(KPT-1、KPT-2)，主管及支管未承受轴力的试件(K-1、K-2)最小。对主管径厚比为39的3个节点，最大值与最小值凹陷量与鼓曲量分别相差4%、6%；主管径厚比为34的3个节点分别相差9%、5%；相较于主管未施加初始荷载的试件，试件KPP-1、KPP-2、KPT-1、KPT-2主管因施加了初始轴拉力，使得冲击过程中主管处于双向受力状态，特别是当主管上表面凹陷时会在主管上表面产生较大的拉力，进而使得主管产生更大的变形；主管施加轴拉力的试件中，相较于两支管分别受拉和受压的试件(KPT-1和KPT-2)，两支管同时受压的试件(KPP-1和KPP-2)对主管下表面位移限制更大一些，因此主管上表面局部凹陷变形分别增大2%、8%。

2.2 冲击力、位移时程曲线

试件K-1、K-2、KPP-1、KPP-2、KPT-1、KPT-2的冲击力以及位移时程曲线，分别如图6(a)～图6(f)所示。其中位移时程曲线包括各试件主管受冲击区域的侧向鼓曲(D1)、侧竖向位移(D2)、管底竖向位移(D3)，以及管侧竖向位移与管底竖向位移之差(D2-D3)。其中KPP-1由于管底位移计没固定牢导致试验中脱落，但仍可看出其变形趋势。参照Qu等的研究，将主管管底竖向位移(D3)定义为主管整体位移，通过管侧竖向位移与管底竖向位移之差(D2-D3)及侧向鼓曲位移(D1)来探究局部变形规律。

图6 冲击力、位移时程曲线

以主管径厚比为34的K形节点试件为例。根据图16中每个试件冲击力时程曲线的发展形式，冲击力及位移时程曲线均可划分分为4个阶段，即：弹性阶段、波动上升阶段、平台阶段、卸载阶段。第一阶段为弹性变形，在锤头与试件接触的瞬间会节点产生弹性激励，所有试件基本未发生变形，冲击力随时间呈线性增长。随后进入第二阶段，主管上表面开始发生类越跃屈曲，冲击力震荡上行。此阶段一开始，对主管及支管未承受轴力的试件K-2，主管管侧竖向位移(D2)与管底竖向位移(D3)时程曲线基本重合，侧壁鼓曲和管侧竖向位移与管底竖向位移之差(D2-D3)时程曲线斜率很小，说明此阶段试件K-2以整体弯曲变形为主；而对主管承受轴拉力支管分别承受轴压或轴拉力的试件KPP-2、KPT-2，其主管管底竖向位移(D3)、侧壁鼓曲变形(D1)以及管侧竖向位移与管底竖向位移之差(D2-D3)时程曲线基本重合，这说明此时试件KPP-2与试件KPT-2主管整体变形与局部凹陷变形速率基本相等。之后，3个试件整体变形速率减小，局部凹陷变形速率增大。到第二阶段后期，试件K-2与试件KPP-2因两支管对主管管底平面内支撑作用使主管整体变形趋于稳定，试件KPT-2因支管对主管管底施加剪力而可以发生剪切变形使得整体变形继续增长。第三阶段，平台阶段因为主管上表面变形过大形成塑性铰使得冲击力变化趋于稳定，并达到峰值；3个试件局部凹陷变形及试件KPT-2主管整体变形继续增大，但增速逐渐减慢；试件K-2与试件KPP-2主管整体变形基本保持不变。第四阶段，卸载阶段，锤头回弹，3个试件弹性形变恢复，但试件K-2侧壁鼓曲变形基本保持不变。

对比图6中主、支管受力状态相同、主管径厚比(γ)不同的试件(K-1与K-2、KPP-1与KPP-2、KPT-1与KPT-2)可以得出：主管径厚比较小(γ=34)的试件冲击持时短，且冲击力峰值分别增大8%、17%、5%，这是因为管壁厚度的增大增加了试件的抗弯刚度。比较相同主管径厚比，主管、支管受力状态不同的试件(K-1、KPP-1、KPT-1和K-2、KPP-2、KPT-2)，KPP-1试件的局部凹陷变形相比试件KPT-1与K-1增大了2%和4%；KPP-2试件的局部凹陷变形相比试件KPT-2、K-2则分别增大了8%和9%，而整体变形最小，这是因为一方面两支管受压可以减小跨中弯矩，进而减小了试件的整体变形；另一方面两个受压支管的存在限制了试件管底的竖向位移，因此，试件只能通过增大局部凹陷变形进行耗能。同时也可以发现主管受拉，支管一拉一压的试件整体变形与局部变形都比较大，这是因为主管轴拉力的存在使冲击过程中主管承受更大拉力，从而使试件的局部凹陷变形增大，而且冲击过程中两个支管分别受拉和受压的状态使主管下表面两支管间隔处发生剪切变形，因此管底竖向位移也较大。

3 抗冲击承载力计算方法的评估

管节点冲击承载力是进行结构动力设计的依据。目前，对管节点承载力的定义主要有以下几种方法：如，Lu等[14]将局部变形为3%D(D为主管直径)时对应的侧向力作为管节点静力承载力；Wang等[15-16]研究钢管构件横向冲击性能时，把冲击力平台值作为构件的稳定承载力；崔安稳等[17]的研究中运用冲量守恒，将求得从锤头开始接触试件到锤头速度第一次为零的过程中试件平均冲击力作为T形管节点的冲击承载力。挪威NORSOK Standard N-004规范[18]、美国API RP 2A-WSD规范[19]、Cerik等[20]分别提出了钢管受撞击时侧向力与局部凹陷变形关系式，并将残余凹陷变形对应冲击力作为冲击承载力(上述定义管节点抗冲击承载力的方法具体公式详见附录A)。这些方法中，Lu等所提出3%D准则需要确定受撞钢管的局部变形，但由于本试验没有测到主管顶部的变形，所以不能通过对位移计变形的换算计算出主管的局部凹陷量，因此该方法不适宜于用来确定本次试验的冲击承载力。本节将对依据以上抗冲击承载力确定方法得到的冲击承载力，与基于试验冲击力时程曲线得到K形管节点抗冲击承载力进行比较，以期确定较为合理的动力设计冲击承载力计算方法。所有的计算结果如表4所示，并绘制成散点图，如图7所示。

表4 试件冲击承载力

图7 冲击承载力评估

分析表4以及图7中可知：Wang等和Yousuf等依据冲击力时程曲线平台值得到的承载力与试验值较为接近；按照动量定理确定的冲击力承载力比试验值偏小；API RP 2A-WSD规范公式计算出的冲击承载力除试件K-2外，均高于试验得到的冲击承载力；而NORSOK Standard N-004规范公式计算出的冲击承载力较为不稳定，试件KPP-1与试件KPT-2计算结果均比试验值要大，其余皆比试验值要小；Cerik等公式计算出的承载力均小于试验值，且两者差距较大；通过以上比较可以得出，API RP 2A-WSD规范公式、NORSOK Standard N-004规范公式计算结果均存在比试验值大的点，作为抗冲击承载力将存在安全隐患；Cerik等公式计算出的结果与试验值相差较大，如果作为冲击承载力较为保守；相比于冲击力时程曲线平台值与按照动量定理确定的冲击承载力，则冲击力时程曲线平台值更接近于试验值，因此冲击力时程曲线平台值作为K形圆管节点的冲击承载力更合适。

4 结论

本文通过对两组主管径厚比不同的K形圆管节点试件进行落锤冲击试验，基于对节点的破坏模态、冲击力、位移时程曲线的分析，揭示了K形圆管节点抗冲击机理，并对国内外相关文献和规范所提出的冲击承载力确定方法进行了比较，得到如下结论：

(1) 冲击过程中，试件主要以主管上表面局部凹陷变形为主，主管整体变形及支管变形不明显，且支管的受力状态使得主管下表面产生3种变形模式，即支管不受力时，主管下表面无明显变形；两个支管同时受压时，两支管与主管相贯处主管下表面出现轻微的向内凹陷变形；一个支管受压另一支管受拉时，两支管与主管相贯处主管下表面表现为受压凹陷和受拉外凸并存的变形模式。

(2) 主管径厚比相同时，主管承受轴拉力两支管同时承受轴压力的试件，主管局部凹陷变形最大，整体弯曲变形最小；受力状态相同的试件中，随着主管径厚比的减小，试件局部凹陷变形减小。

(3) 试件冲击力时程曲线形状相似，受力状态相同时，主管径厚比大的试件冲击持时更长且冲击平台更低。

(4) 冲击荷载作用下的K形管节点，以冲击力时程曲线的平台值作为节点的抗冲击承载力较为合理。

附录A

(1) 冲量定理方法

假设从锤头开始接触试件到锤头速度第一次为零的过程中，锤头受力均为来自试件的冲击力反力。根据冲量守恒，通过以下公式来计算平均冲击力

(A.1)

式中：m为落锤的质量； Δv为落锤与主管接触前达到的最大速度； Δt为落锤与主管接触开始到速度第一次降为零的时间。

(2) 挪威NORSOK Standard N-004规范公式

(A.2)

(A.3)

(A.4)