落石冲击砂垫层的动力响应数值分析

2022-03-27王海生张锦华张亚栋李巧生

振动与冲击 2022年6期

王海生，张锦华，陈力，张亚栋，李巧生

(1. 陆军工程大学爆炸冲击防灾减灾国家重点实验室，南京 210007；2. 东南大学爆炸安全防护教育部工程研究中心，南京 211189)

含缓冲垫层的钢筋混凝土结构是山区落石防护的典型结构，在山区落石灾害防护中被广泛使用[1-2]。粗砂等是工程中防落石结构最常用的垫层材料[3-4]，其具有良好的缓冲性能，同时取材方便、耐久性好、经济效益高、透水性好。落石冲击含砂垫层的防护结构主要涉及3个关键问题：一是落石与砂垫层的相互作用；二是压缩波在砂垫层中的传播与衰减；三是防护结构的动力响应。已研究表明[5]，落石冲击砂垫层，是一个脉冲式的冲击过程，冲击力在几到几十毫秒内达到极大值，而后又迅速衰减，但冲击力在砂垫层中如何传播并作用在防护结构上，是当前研究尚未完全解决的问题。在设计防落石结构时，工程师最关心的问题是作用在防护结构上的冲击力和分布范围，因为这决定了防护结构的设计。为了研究落石冲击力的形成与传播规律，许多学者进行了理论、试验和数值模拟研究。

理论分析主要基于Hertz碰撞理论、冲量定理和功能原理。Hertz碰撞理论，假设落石与垫层为弹性体，接触面为光滑的球面，求得接触压力与法向变形的关系，但与实际情况差别较大[6-7]。Thornton等[8-9]对Hertz弹性理论进行了弹塑性修正；Walton等[10]对Thornton的弹塑性模型参数进行了简化，但都求解困难。基于冲量定理[11]和功能原理[12]获得的结果为平均冲击力，比实际冲击力小。由于理论求解困难，一些学者进行了落石冲击试验研究，Sasaki等[13-17]进行了砂垫层对落石缓冲的试验研究，认为落石冲击砂垫层会产生压缩波，影响冲击力大小。但试验成本高，只能获得宏观上的测试结果，无法深入研究砂垫层中压缩波的传播规律。Calvetti等[18-20]使用数值模型研究了落石冲击砂垫层的冲击效应。Zhang等[21]采用离散元模型分析了砂垫层中能量耗散的过程。Fang等[22]使用三维细观模型研究了砂在动荷载下的颗粒级响应。上述数值模拟均对砂中压缩波传播进行了深入分析，但计算效率低，对大尺寸砂垫层模拟困难。

近年来，有限元模型(finite element method，FEM)广泛用于动力响应分析，其计算稳定高效，能较好模拟大尺寸砂垫层受冲击的过程。Fasanella等[23]运用FEM模拟了太空舱冲击砂垫层的过程，与试验结果吻合良好，但其模型参数获取困难，依赖于大量的试验。本文提出了一种落石冲击砂垫层动力响应的数值分析方法。首先，分析了LS-DYNA软件中MAT_SOIL_AND_FOAM(SAF)材料模型的屈服面参数与砂的内摩擦角和黏聚力的关系，便于确定砂的模型参数。其次，建立了落石冲击砂垫层的有限元模型，与现有试验数据进行比较，验证了模型的可靠性，进一步分析了落石质量、冲击速度、冲击角度、砂垫层厚度和密度对冲击效应的影响。再次，以砂中压缩波的扩散角、衰减系数和冲击力传递系数，量化分析了砂中压缩波的传播和衰减规律。最后，以应力波在锥杆中的传播理论，初步讨论了砂中压缩波的传播过程和相互作用机理。

1 砂的本构模型及参数确定方法

1.1 砂的本构模型

砂为松散孔隙岩土材料，在冲击荷载下具有流体特性，体积压缩规律能描述砂在冲击受压过程中的减缩特征。Zhang等的研究表明，砂垫层与落石接触面中心点附近主要处于三向压缩状态，远离中心点的侧面主要处于剪切状态，砂的压缩程度取决于压力，因此可采用压力与体积的关系来描述砂的压缩过程。LS-DYNA软件中的SAF材料模型[24]对该关系具有很好的描述，其剪切屈服特征采用正应力与偏应力之间的二次函数表示

J2=a0+a1p+a2p2

(1)

式中：J2为应力偏量的第二不变量；p为静水压力；a0、a1、a2为屈服面参数。

若采用D-P(Drucker-Prager)屈服准则，可确定参数a0、a1、a2与内摩擦角φ、黏聚力C的关系

(2)

SAF模型用压力与体积应变的关系描述状态方程，其中体积应变是当前体积V与初始体积V0之比的自然对数ln(V/V0)，压缩状态为负值，拉伸状态为正值。

p=f[ln(V/V0)]

(3)

将ln(V/V0)展开为泰勒级数，有

(4)

式中，εV=V/V0-1。

根据式(3)和式(4)，得

(5)

式(5)满足固体的Hugoniot状态方程。

Felice等[25-29]研究表明，砂的力学性能与应变率关系不大，如图1所示。落石冲击属于低速冲击，砂垫层受落石冲击的应变率较低，一般在1 s-1以内，故本文采用的砂模型忽略应变率的影响。

图1 砂的应力应变曲线(Song等的研究)

1.2 确定屈服面参数的算例

Thomas等[30-31]的研究中砂的SAF模型参数为试验所得，本文将式(2)计算的参数a0、a1、a2与文献试验结果对比，证明该方法确定的屈服面参数是合理的，如表1所示。

表1 Thomas等的研究中砂SAF模型参数的试验和本文理论结果对比表

2 数值计算及分析

Calvetti等对落石斜冲击砂垫层、正冲击砂垫层、重复冲击砂垫层和冲击轻质陶瓷骨料4组工况进行了试验研究，本文选用其第二组工况进行数值模拟分析。

2.1 有限元模型的建立

2.1.1 模型尺寸与边界条件

根据试验给定的条件，建立了落石冲击砂垫层的三维有限元模型，如图2所示。落石为直径0.9 m的球；砂垫层厚2 m，为减小计算量，边界尺寸从试验的10.7 m改为4.8 m，并在侧面施加无反射边界条件，以近似消除侧边界反射波对模拟结果的影响；混凝土板厚0.2 m，在底面设置全约束，在与YOZ平面平行的侧面节点上施加X轴方向位移约束和绕Z轴和Y轴旋转的转动约束，在与XOZ平面平行的侧面节点上施加Y轴方向位移约束和绕Z轴和X轴旋转的转动约束。

图2 有限元模型(m)

2.1.2 模型参数

落石的变形模量比砂垫层高几个数量级，且冲击速度较低，冲击过程中落石很少发生塑性变形和破裂，故采用弹性材料模型[32]，根据落石的质量和半径推算密度为2 227 kg/m3，参考普通混凝土力学性能，取落石的弹性模量为36 GPa，泊松比为0.24。

砂垫层选用SAF模型，密度为1 500 kg/m3，内摩擦角为30°，黏聚力为3 500 Pa，根据式(2)计算a0、a1、a2。Brown等[33]对砂的状态方程进行了试验研究，发现幂次律P-α理论模型与试验数据吻合较好，本文采用其理论和数据描述砂的状态方程，砂的主要参数如表2所示，所有单位采取国际单位制。

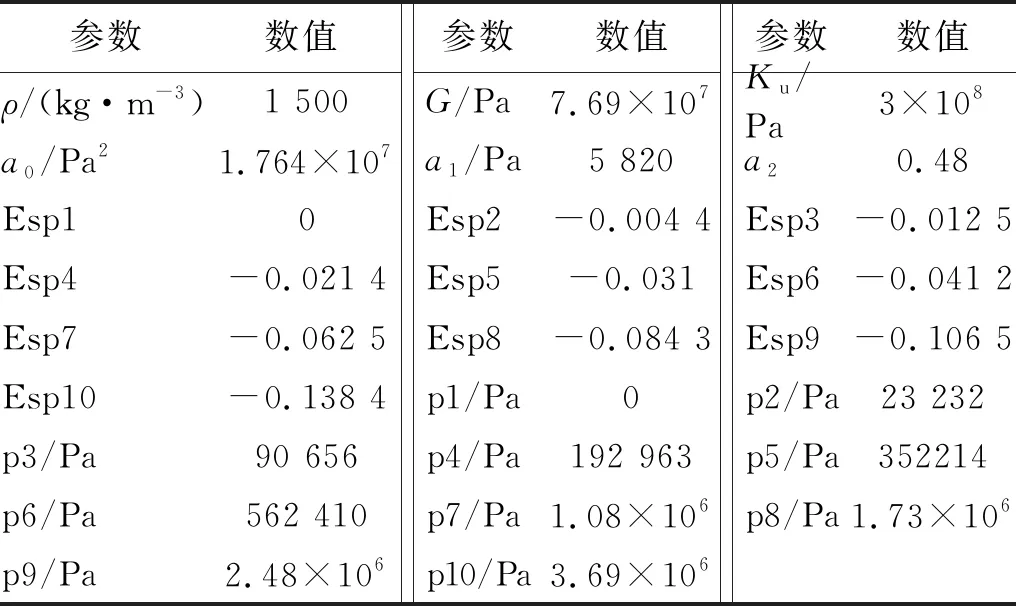
表2 砂垫层材料模型参数

混凝土板采用MAT_CONCRETE_DAMAGE_ REL3[34]材料模型，密度为2 400 kg/m3，泊松比为0.24，抗压强度为30 MPa。

落石与砂垫层、砂垫层与混凝土板均采用自动面面接触。岩土间摩擦因数常见取值范围为0.25～0.40，数值计算结果表明其对球形落石冲击效应影响不大，本文取动摩擦因数为0.25，最大静摩擦因数为0.30。

2.1.3 单元尺寸的敏感性分析

落石与垫层材料均采用六面体单元，其中，落石与砂垫层单元尺寸分别为2 cm和4 cm，共84.8万个单元。为了检验单元尺寸对计算结果的影响，进行了单元尺寸的敏感性分析，在原模型的基础上，将单元尺寸缩减一倍，即落石与砂垫层单元尺寸分别为1 cm和2 cm，单元总数量约339.2万。计算结果表明，在相同条件下，两个模型的冲击效应计算结果十分接近，加速度峰值和冲击深度分别相差1.2%和1.5%。因此，综合计算精度和效率，本文采用落石2 cm、砂垫层4 cm的单元尺寸。

2.2 数值计算与试验结果对比

以Calvetti等研究中Test n.6工况为例，质量850 kg的落石以14 m/s速度冲击2 m厚砂垫层，其模拟与试验结果如图3所示，以落石与砂垫层开始碰撞时为零时刻。图3(a)显示的是落石加速度时程曲线(本文没有特殊说明均指法向加速度)，在0.02 s之前，模拟与试验的曲线十分接近，模拟峰值为279 m/s2，试验峰值为270 m/s2，相差3.33%。0.02 s之后，模拟结果小于试验结果，可能是因为试验中砂垫层不是均质材料，砂的体积模量随着深度增加而增大，压缩波会反射，导致砂垫层与落石接触面应力增大，所以试验中出现了第二峰值，加速度下降的更快，本文主要研究砂垫层的动力响应峰值，从峰值角度看，模拟结果与试验结果相差不大。图4(b)显示冲击深度的模拟结果与试验数据相差不大，模拟结果为0.58 m，试验结果为0.56 m，相差4.8%。上述结果表明，模拟结果与试验结果吻合良好，该模型能够模拟落石冲击砂垫层的过程。

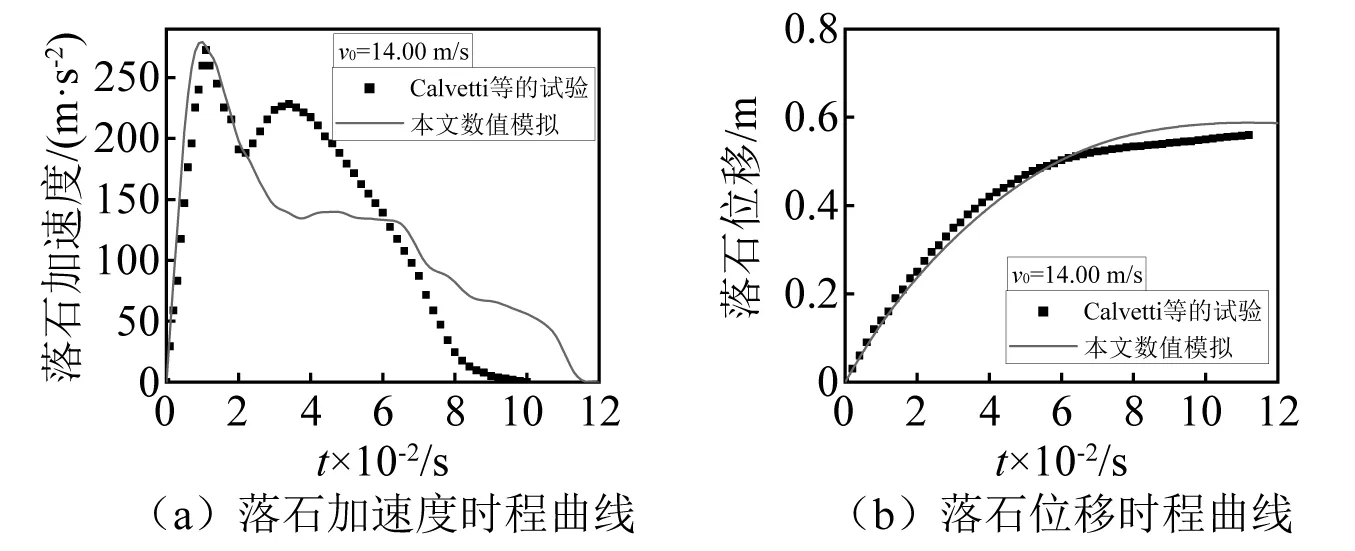
图3 Test n.6数值模拟与试验结果对比

根据上述模型参数，模拟冲击速度为19.02 m/s的工况Test n.8，模拟与试验结果如图4所示，模型曲线与试验曲线比较接近，故本文的模型可用。

图4 Test n.8数值模拟与试验结果对比

2.3 砂垫层参数分析

砂的力学性能是影响落石冲击效应的重要因素，本文已经研究了砂的内摩擦角和黏聚力对砂力学性能的影响，下面分析砂的厚度和密度对落石冲击效应的影响，选取典型落石工况，质量为850 kg、冲击速度为14 m/s。

2.3.1 砂厚度的影响

根据TB 10003—2005《铁路隧道设计规范》，垫层的厚度一般不小于1.5 m，选砂厚度的变化范围为1.0～2.0 m。落石对不同厚度砂的冲击效应，如图5所示。结果表明，砂的厚度对落石加速度峰值没有明显影响；随着砂厚度的增加，冲击深度从57.8 cm减至55.9 cm，变化不明显，故砂厚度对冲击深度的影响也可以忽略。定义砂垫层底面对混凝土板的冲击力为传递冲击力F1，则图5(c)显示随着砂厚度的增加，传递冲击力峰值减小，且减小的幅度越来越小。该结论在Kawahara等的试验中也有出现。本文砂的厚度增至1.6 m后，传递冲击力峰值变化不大，工程中增加砂的厚度会增大砂的自质量，故在该典型落石工况中砂垫层最佳厚度为1.6 m。

图5 砂垫层厚度对落石冲击效应的影响

2.3.2 砂密度的影响

JTG D30—2015《公路路基设计规范》常用的垫层密度范围为1 000～2 000 kg/m3，本文选取砂密度变化范围为1 000～2 000 kg/m3。落石对不同密度砂的冲击效应，如图6所示。结果表明，落石加速度峰值与砂密度呈指数增大关系，冲击深度与砂密度呈指数衰减关系，随着砂密度增大，传递冲击力峰值增大，且增大的幅度越来越小，当砂密度增大到1 400 kg/m3后，传递冲击力峰值变化不大，Kawahara等和Zhang等得出同样的结论。

图6 砂垫层密度对落石冲击效应的影响

上述计算结果表明砂垫层的厚度越大，落石受到的阻力变化不大，冲击深度减小幅度不大，对底面混凝土板的传递冲击力越小，故工程中砂垫层的厚度不能太小，否则无法达到减小冲击力的目的，但也不能过大，因为增加砂垫层厚度会增加砂的自质量对防护结构的静载作用，也不经济。砂垫层的密度越大，落石受到的阻力越大，冲击深度越小，对底面混凝土的传递冲击力越大，故工程中砂垫层倾向于选择松砂，即砂垫层密度相对较小，但也需注意落石冲击深度，不能大于砂垫层厚度，否则会损伤防护结构。

2.4 落石参数分析

下面分析落石质量、冲击速度、冲击角度对冲击效应的影响，根据2.3节砂垫层参数分析结果，选取砂的厚度为1.6 m，密度为1 500 kg/m3。

2.4.1 落石质量的影响

研究表明[35]，90%落石质量小于1 360 kg，平均质量460 kg，最大质量4 500 kg，选取落石质量变化范围为50～2 500 kg。不同落石质量对砂垫层的冲击效应，如图7所示。结果表明，落石加速度峰值与质量呈指数衰减关系，冲击深度与落石质量呈指数增大关系，传递冲击力峰值与落石质量呈指数增大关系。Kawahara等得出同样的结论。

图7 落石质量对冲击效应的影响

2.4.2 冲击速度的影响

Wyllie的研究表明，落石冲击速度的分布范围为10～42 m/s，平均值为26.2 m/s，本文选取冲击速度为10～45 m/s。落石以不同冲击速度对砂垫层的冲击效应，如图8所示。结果表明，加速度峰值与冲击速度呈指数增大关系，冲击深度与冲击速度呈指数增大关系，传递冲击力峰值与冲击速度呈指数增大关系。

图8 落石冲击速度对冲击效应的影响

2.4.3 落石冲击角度的影响

定义冲击速度与砂垫层表面的角度为冲击角度λ。Wyllie的研究表明，冲击角度的分布范围为60°～65°，为扩大分析范围，选取冲击角度变化范围为45°～90°。落石以不同冲击角度对砂垫层的冲击效应，如图9所示。结果表明，加速度峰值、冲击深度和传递冲击力峰值都与冲击角度是正弦函数的指数关系。因为冲击速度与冲击角度满足正弦函数关系，冲击角度的增大，相当于冲击速度的增大，所以冲击角度对落石冲击效应的影响，可以等效于冲击速度对冲击效应的影响。

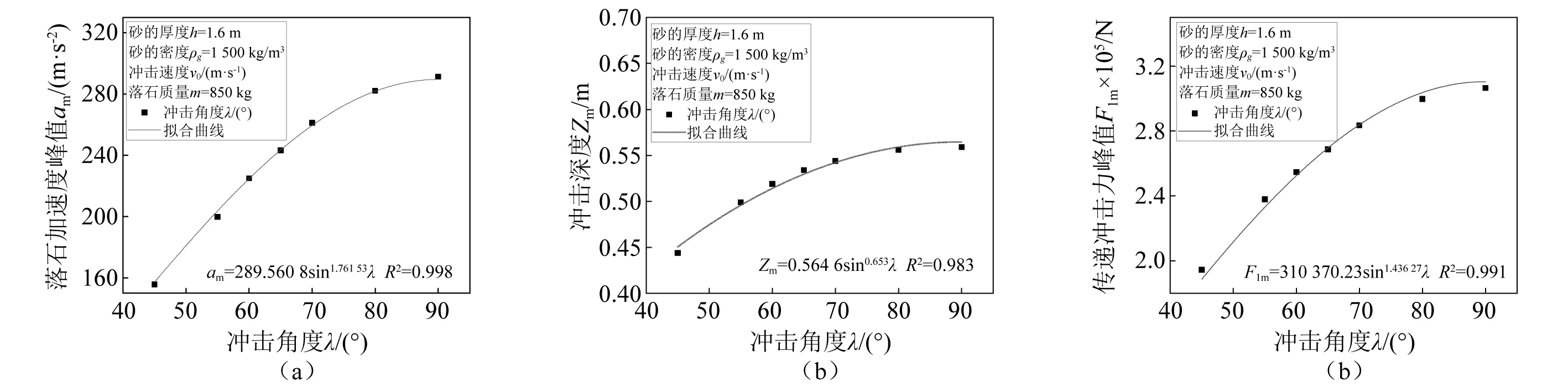
图9 落石冲击角度对冲击效应的影响

3 砂垫层缓冲性能分析

3.1 扩散角

研究表明[36-38]，落石冲击砂垫层形成的压缩波以冲击点开始呈锥角向底面传播。将砂垫层顶层和底面应力边界的连线与垫层表面法线夹角定义为扩散角θ，如图10所示。扩散角对于研究作用在结构上力的作用范围具有重大意义，假设扩散角为θ，则冲击力在砂垫层底面的扩散半径L为

图10 扩散角示意图

L=R+htanθ

(6)

式中：R为落石与垫层接触面的半径，R≤落石半径r；h为砂垫层厚度。

目前对于扩散角没有统一的规范，TB 10003—2005《铁路隧道设计规范》中为40°，JTG D30—2015《公路路基设计规范》中为35°，以上给出的扩散角只是一个经验值，落石冲击砂垫层的过程中，扩散角不是一个恒定值，与动荷载和砂垫层力学性能相关，试验中砂垫层材料不可能是均质材料，这也导致扩散角不是一个恒定的值，因此本文采用数值模拟的方法研究扩散角的规律。

由于不同工况砂垫层底面应力范围难以确定，为使扩散角不大于规范中最大值40°，以砂垫层最大应力的0.7%作为底面扩散边界。落石质量850 kg，冲击速度14 m/s、砂厚1.6 m、密度1 500 kg/m3工况的不同时刻扩散角，如图11所示。图11(a)显示砂垫层最大应力为2.116 MPa，以15 kPa作为砂垫层底面应力边界，可得到扩散角的大小。图11(b)～图11(d)分别表示砂垫层底面应力范围最大时刻、传递冲击力最大时刻和落石与砂垫层接触面最大时的扩散角，为25.2°、18.5°、15.5°，为使防护结构安全可靠，取其最大值作为该工况的扩散角θ=25.2°。

图11 工况1不同时刻的扩散角

落石质量850 kg、冲击速度14 m/s、砂厚2.0 m、密度1 500 kg/m3工况的不同时刻扩散角，如图12所示。图12(a)显示砂垫层最大应力为2.116 MPa，扩散角边界没有变化。图12(b)～图12(d)分别上述3个时刻的扩散角，取最大值作为该工况的扩散角θ=16.9°。

图12 工况2不同时刻的扩散角

落石质量850 kg、冲击速度14 m/s、砂厚2.0 m、密度1 800 kg/m3工况的不同时刻扩散角，如图13所示。图13(a)显示砂垫层最大应力为2.43 MPa，以17 kPa作为砂垫层底面应力边界。图13(b)～图13(d)分别上述3个时刻的扩散角，取最大值作为该工况的扩散角θ=13.7°。

技道合一的论点在中国艺术创作中产生了深远的影响。宋苏轼就曾在《书李伯时山庄图后》提出“有道而不艺，则物虽形于心，不形于手”的观点。明郑板桥用“眼中之竹”、“胸中之竹”、“手中之竹”来概括其艺术创作的全过程,可是从“胸中之竹”道“手中之竹”必须有高度娴熟的技巧方可达到,“必极工而后能写意”,写意的前提是“极工”，差一点不得。由此观之，中国传统艺术所追求的极致就是“技道合一”。

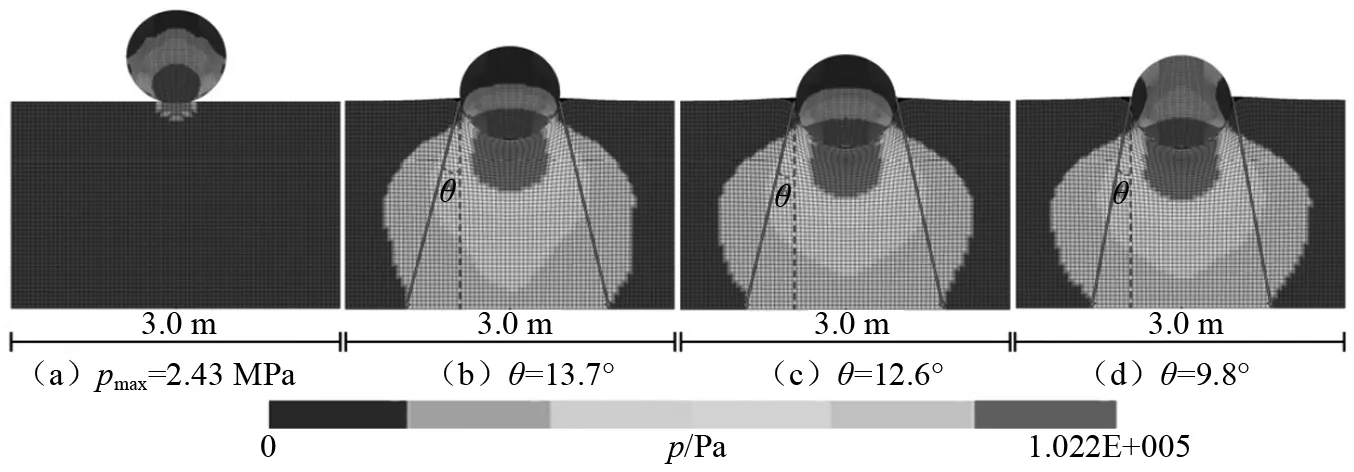
图13 工况3不同时刻的扩散角

砂垫层参数对扩散角的影响，如图14所示。图14(a)表明扩散角随砂厚度的增大而减小，这是由于砂垫层受落石冲击的最大应力与砂的厚度无关，当砂厚度增加时，传到砂垫层底面的应力随着砂厚度的增加而减小，对应的应力的边界范围缩小，致使扩散角减小。图14(b)表明，扩散角随砂的密度增加而减小，且减小的幅度越来越小。

图14 砂垫层参数对扩散角的影响

落石参数对扩散角的影响，如图15所示。图15(a)表明，扩散角随落石质量增大而增大，当落石质量小于临界值时，砂垫层底面应力为零，扩散角为零；图15(b)表明，扩散角随冲击速度增大而增大，且增大的趋势越来越大。

图15 落石参数对扩散角的影响

3.2 衰减系数

Szendrei[39]提出在有界介质中，波速振幅随着传播距离的衰减规律为

A(z)=A0z-n

(7)

式中：z为传播距离；A0为初始振幅；A(z)为z处振幅；n为衰减指数，与垫层性质和边界条件有关。

以落石与砂垫层接触面中心点应力峰值为初始应力σ0，接触面中心点正下方深度z处的应力峰值为σz，定义衰减系数

ζ(z)=σz/σ0

(8)

对于同一深度z，落石和砂的参数对衰减系数ζ的影响，如图16所示。结果表明，衰减系数ζ随落石质量的增大而增大，随落石冲击速度先增大后减小，与砂的厚度和密度关系不大。

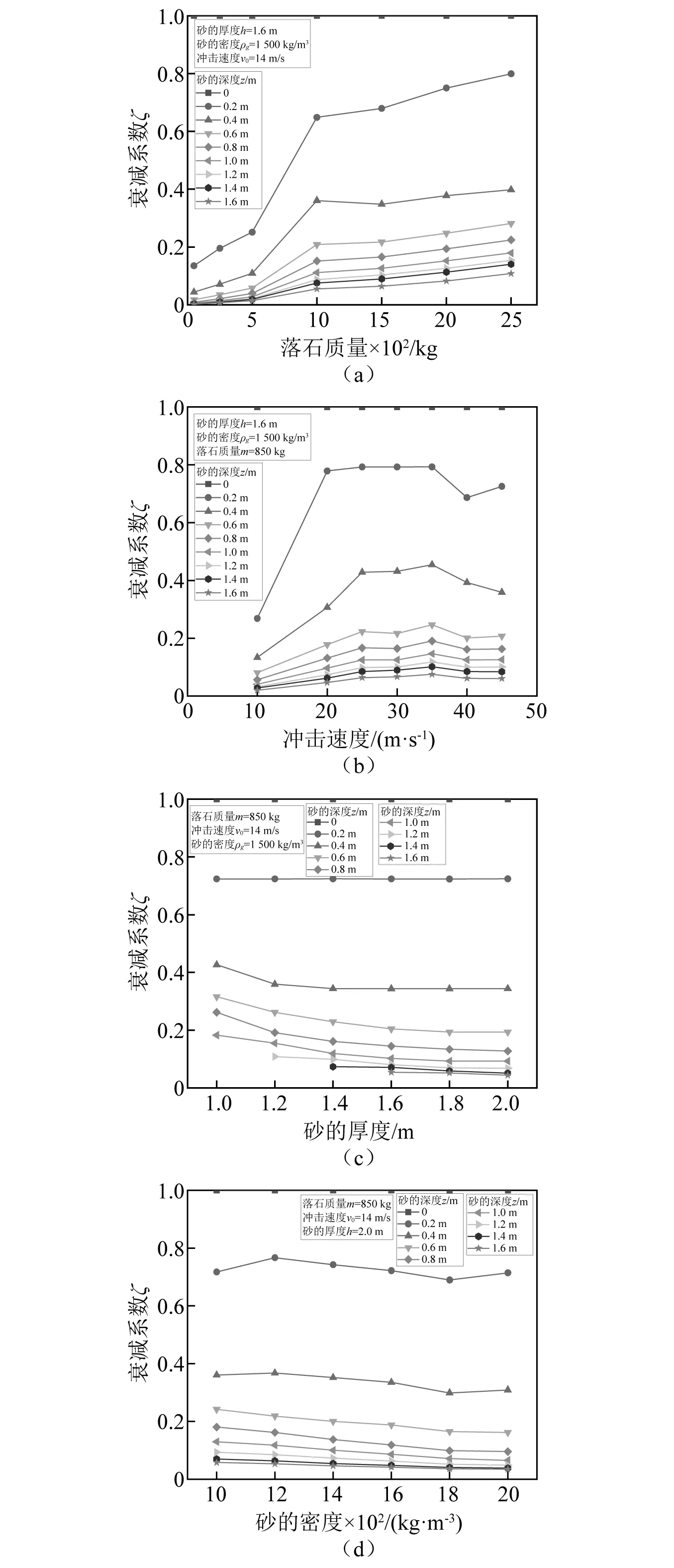
图16 落石和砂的参数对衰减系数的影响

通过以上分析可知，衰减系数与落石质量、冲击速度和砂中深度关系较大，与砂垫层参数关系不大。

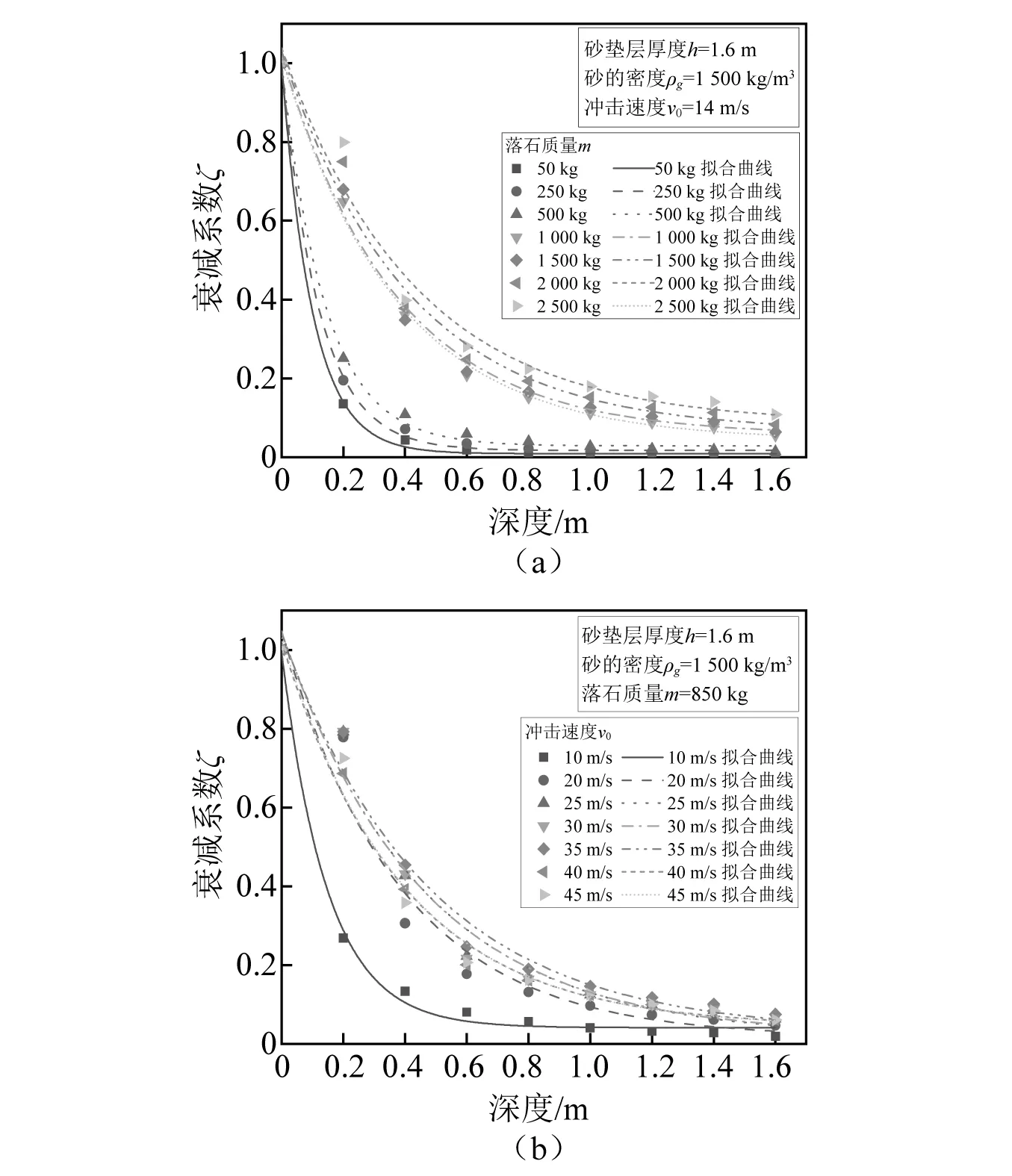
图17 不同工况下衰减系数随砂垫层深度的关系

因此通过衰减系数可以分析砂垫层对压缩波的衰减程度。对衰减系数与砂垫层深度关系进行拟合，可以得到式(8)，拟合函数的相关系数均大于0.85。

ζ(z)=Be-z/ω

(9)

式中：B与砂垫层参数有关；ω与落石尺寸和密度有关；z与砂垫层深度有关。

对于本文所涉及的砂垫层拟合值B为0.95～0.99，涉及落石的拟合值ω为0.10～0.45。落石质量越大，对应的ω越大。

3.3 传递系数

研究表明[40]，落石冲击过程中，落石重力对落石冲击力的影响不超过10%，故本文忽略落石重力对冲击效应的影响，假定落石冲击力F0近似等于落石加速度与质量之积，则定义传递系数

γ=F1max/F0max

(10)

图18(a)表明随着砂的厚度增大，传递系数减小，且减小的幅度越来越小，当砂的厚度增大到临界值后，传递系数变化不大；图18(b)表明传递系数与砂垫层密度呈指数减小的关系，该结论在Calvetti等的试验结果中也出现了；图18(c)表明传递系数与落石质量的呈指数增大关系；图18(d)表明传递系数随冲击速度的增大而减小。图18中所有传递系数γ都介于1～2，符合压缩波在不同介质界面上的传播规律。

图18 砂和落石参数对传递系数的影响

4 落石冲击砂垫层的机理分析

砂垫层受落石冲击的过程中，砂的颗粒结构和颗粒之间的接触都发生变化和破坏，砂的应力状态也随之变化，以落石质量850 kg、冲击速度14 m/s、砂垫层厚度2.0 m、密度1 500 kg/m3的工况为例，其应力云图如图19所示。

图19(a)为落石刚接触砂垫层时的应力云图，落石与砂的接触面较小，近似为点面接触，砂垫层中的应力非常大，但只分布于冲击点附近半球形区域。随着落石与砂垫层的接触面增大，应力在砂中向四周传播，图19(b)为落石冲击力F0达到峰值时的应力云图，砂垫层中沿落石运动轨迹的应力迅速增大，靠近冲击点的应力高于接触面边缘的应力。图19(c)为压缩波传播到混凝土板时的应力云图，可以看出，在接触面中心区域的砂主要以三向压缩为主，在边缘附近区域的砂主要以剪切变形为主，且压缩为主的区域，越靠近接触面的区域应力越大。图19(d)为砂垫层底面应力分布范围最大时的应力云图，由于混凝土板刚度较大，可将砂垫层与混凝土板的交界面看作固定端，压缩波经交界面反射形成反射波，应力边界范围由原来的球形变成了椭球型，是由于后续的压缩波与反射波共同作用形成的。图19(e)为落石冲击速度为零时的应力云图，砂垫层中的应力没有后续冲击补充，应力变小，分布范围越来越小，向冲击点“收缩”，砂处于卸载状态，直至冲击过程结束。

图19 落石冲击砂垫层应力传播过程

参考王礼立等[41-43]锥杆中应力波传播的理论，将与落石接触的砂垫层看作压缩波入射端，直径为2r，砂垫层底面应力分布范围看作反射端，直径为2L，锥角为扩散角θ，则压缩波在砂垫层中的传播可以简化为由锥体的小端向大端传播，锥体的截面积按扩散角由小变大，如图20所示。由该理论可知，锥杆的长径比2L/h对砂垫层底面的应力峰值的衰减影响很大，且同一截面上各点应力值不同，截面中心点应力比边缘大。

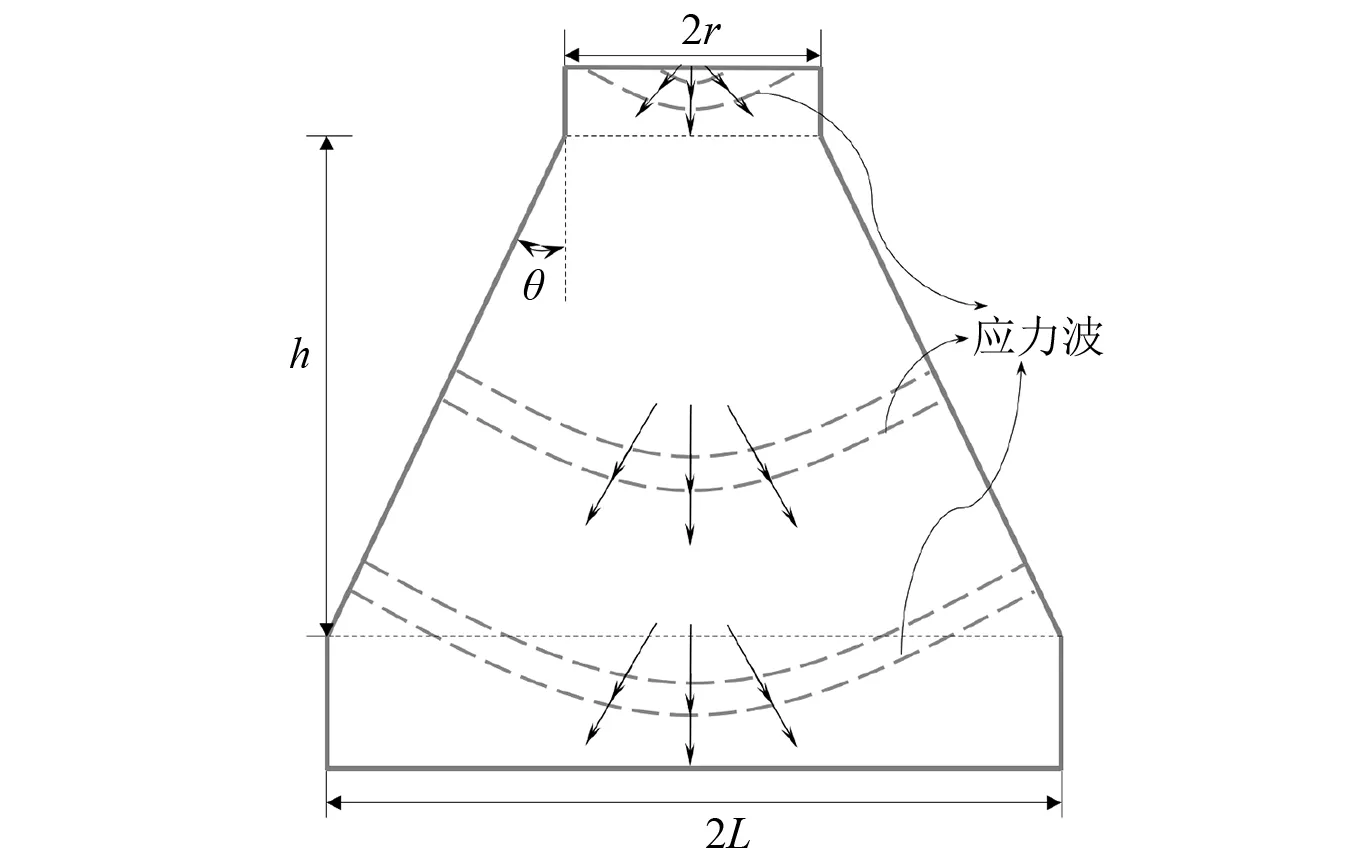
图20 锥杆应力波传播示意图

综上所述，可将落石冲击砂垫层动力响应简化为锥杆中压缩波传播，其作用过程如图21所示，图21(a)为落石冲击锥杆砂垫层，在锥杆顶面形成压缩波；由于压缩波传播速度远大于落石冲击速度，压缩波向锥杆底面快速传播，如图21(b)所示；压缩波中心区域的应力水平大于两侧的应力，其波速也稍大，与图19(b)所显示的计算结果基本一致；压缩波传播至锥杆底面时，经交界面形成反射波，如图21(c)所示；反射波沿着向上的方向在锥杆中传播，并与向下传播的压缩波相互作用并叠加，如图21(d)所示，在锥杆中该作用过程持续发生，直至压缩波衰减至零，如图21(e)所示。