双模交叉克尔型耦合系统中宏观量子叠加态的制备
2022-03-26韩佳秀龙玉梅孙迎春郑泰玉
韩佳秀,龙玉梅,郑 丽,张 雪,孙迎春,郑泰玉
(1.东北师范大学物理学院,吉林 长春 130024;2.大连工业大学基础教学部,辽宁 大连 116034)
光与物质的相互作用是腔光力学的核心[1-3].是光机械系统中的各种量子相干效应的根源.腔光力学的研究主要是对腔机械耦合的理解、操作与开发应用,对探索两量子理论基本原理和现代量子技术有着重要的意义.腔光力学系统因为其可以观测研究宏观物体的量子特性,最近引起了人们极大的研究兴趣.特别是光力腔中只有少数光子的情况[4-11].因为在这个区域,光力腔具有非线性特征,会增强许多有趣的现象,比如空腔阻塞和宏观量子相干性等.但是少光子光力效应在实验中很难观察到,因为效应远小于噪音的影响.许多科学家正在从事如何增强单光子情况下的光力耦合,比如力学谐振腔阵列[12]、约瑟夫森结非线性应用[13-15]、量子放大等[16].
交叉克尔效应目前在量子态的制备[17-18]、量子通信协议[19-22]、光子计数[23]中应用非常普遍.最近,有人提出通过交叉克尔效应耦合来实现少光子的腔力系统中的超强耦合.这里超强耦合的定义是单光子耦合强度能够达到力学谐振子频率的数量级程度[24].
本文提出利用交叉克尔效应在光力系统来制备宏观量子叠加态,并讨论其相干性的特点等.
1 理论模型
考虑一个二能级原子-光力系统,其中包含一个二能级原子、光腔和机械振子、二能级原子放置在一个单模光腔中,其相互作用可以用JC模型来描述,光腔包含一个固定反射镜和一个可移动反射镜,可移动反射镜与光场之间通过辐射-压力相互作用(即光机耦合)耦合,本文考虑单模机械振荡的单模腔场,两模式间的相互作用为交叉克尔相互作用.光力耦合系数是近共振可调谐的.因此,该系统的哈密顿量为
(1)
其中:a是光场的湮灭算符,σi是原子算符,b是机械振子的湮灭算符,Ω是原子与腔的耦合系数,g是机械振子与光腔的单光子光力耦合系数,ω和ωM分别是光腔和机械振子率.设原子和腔共振,χ为交叉克尔相互作用强度.
若考虑原子与腔相互作用强耦合的情况η=Ω/ω≥0.1,在二阶近似下,文献[25]利用微扰论给出了低能级子空间中的有效哈密顿量,H的有效哈密顿量可写为
Heff=ω+|+〉〈+|+ω-|-〉〈-|+ωMb†b+[ɡ(b+b†)-χb†b](α+|+〉〈+|+α-|-〉〈-|+ξ).
(2)
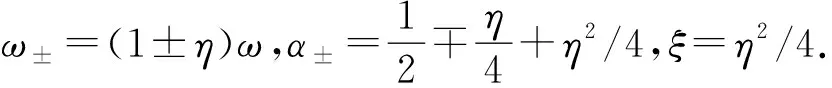
(3)
(4)
变换到相互作用表象
(5)
在-χb†b的旋转框架下,上述哈密顿量可以进一步写为
(6)
其中δ=ωM-χ.由Wei-Norm方法可得演化算符
UI(t)=ef1|+〉〈+|bef2|-〉〈-|bef3|+〉〈+|b†ef4|-〉〈-|b†ef5|+〉〈+|ef6|-〉〈-|ef7bef8b†ef9,
(7)
其中:
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
2 宏观量子叠加态的制备
t=0时刻,设系统的初态|+0〉,|0〉为机械振子真空态,计算出t时刻,系统的演化态为
|Ψ(t)〉+I=UI(t)|+0〉=eP++iQ+|+〉|γ+〉.
(17)
其中:
γ+=f3+f8;
同理可得:t=0时刻,设系统的初态为|-0〉,|0〉为机械振子真空态,计算出t时刻,系统的演化态为
|Ψ(t)〉-I=eP-+iQ-|-〉|γ-〉.
(18)
其中|γ-〉为机械振子的相干态,且
γ-=f4+f8,
变换到薛定谔表象,系统的波函数为
|Ψ(t)〉±=eP±+iv±(t)|±〉|β±〉.
(19)
其中|β±〉为机械振子的相干态,且
(20)
(21)

(22)
其中:
(23)
(24)
(25)
|φ3ɡ〉m=[eP++iv+(t)|β+〉-eP-+iv-(t)|β-〉].
(26)
|φ1ɡ〉m,|φ0e〉m,|φ2e〉m,|φ3ɡ〉m均为宏观叠加态.但是|φ2e〉m,|φ3ɡ〉m的几率极小,后面的分析中我们近似将其忽略.可以看出,若对腔和原子进行测量,不管其结果是|1g〉还是|0e〉,机械振子的状态都会处在相应的叠加态|φ1ɡ〉m或|φ0e〉m.
3 叠加态的宏观可区分性及其量子相干性的讨论
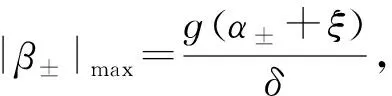
最后,分析一下两个相干态之间的量子相干性,以|φ0e〉m态为例,其wigner函数为
(27)

假设ωM=20ɡ,η=0.1,点划线对应δ/ɡ=0.03,实线对应δ/ɡ=0.01,虚线对应δ/ɡ=0.005.
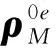

ωM=20ɡ,η=0.1,δ=0.01ɡ,t=π/δ
4 总结
本文考虑单模光腔中放置一个二能级原子并且考虑强耦合情况,光腔与一个单模的机械振子通过交叉克尔效应进行耦合,发现交叉克尔效应耦合强度接近于机械振子的振动频率时,机械振子的机械位移可以被放大,并实现可区分的宏观量子叠加态的制备.
