分数阶Like-Bao系统自适应滑模同步的整数阶滑模面设计

周长芹，毛北行，王东晓

(郑州航空工业管理学院数学学院，河南 郑州 450015)

0 引言

混沌系统具有对初始条件及参数变化的敏感性，因而备受人们关注，其在保密通讯、信号与处理、经济学、物理学及控制学科等领域被广为应用.伴随着分数阶微积分这一学科的发展，越来越多的科研人员逐渐关注到此类同步控制并把该问题作为研究的热点[1-3].文献[4]进行了分数阶Duffling系统混沌终端滑模同步问题的研究；文献[5]对分数阶Genesio-Tesi系统的适应转移滑模同步问题进行了研究；文献[6]运用了两种不同的滑模方法，对分数阶Newton-Leipnik系统的同步问题进行了探讨；文献[7]给出分数阶比例积分滑模面的设计与构造；文献[8]研究了一类神经网络系统的有限时间同步；文献[9]对一类分数阶时滞神经网络系统的有限时间同步问题进行了研究与分析.同时，很多专家学者对Like-Bao系统的同步控制进行了研究.文献[10]基于比例积分滑模方法，对分数阶超混沌Bao系统同步进行了研究；文献[11]给出了超混沌Like-Bao系统的混沌运动及动力学分析方面的研究结果；文献[12]探讨了一类超混沌Bao混沌系统的线性反馈同步问题.本文构造了新的整数阶滑模函数以及自适应规则，对分数阶Like-Bao混沌系统滑模同步问题进行了研究，得到分数阶Like-Bao混沌系统自适应滑模同步的充分条件.

1 系统描述和主要研究结果

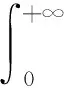
定义1[13]Caputo分数阶导数的定义为

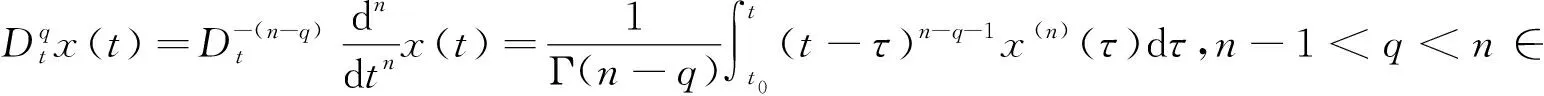
分数阶Like-Bao系统描述为[14]

(1)

当a=38，b=6，c=20，k=2，q=0.896时，吸引子如图1所示.

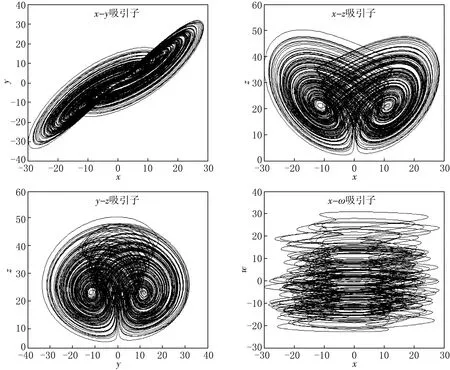
图1 系统吸引子

设计从系统如下：

(2)

其中：φ(t)=[x1，y1，z1，ω1]T，Δfi(φ(t))为有界不确定项，di(t)为有界外扰.定义e1=x1-x，e2=y1-y，e3=z1-z，e4=ω1-ω，从而有

(3)

假设1 存在未知常量mi，ni(mi，ni>0)，满足|Δfi(φ(t))|≤mi，|di(t)|≤ni.

定理1 构造滑模面si(t)=ei，控制输入为

自适应规则为

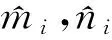
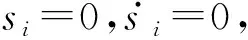
因为si(t)=ei，故

整数阶Like-Bao混沌系统可描述为

(4)

从系统设计为

(5)

其中：φ(t)=[x1，y1，z1，ω1]T，Δfi(φ(t))为有界不确定项，di(t)为有界外扰.定义e1=x1-x，e2=y1-y，e3=z1-z，e4=ω1-ω，从而有

(6)

定理2 构造滑模面si(t)=ei，控制输入

自适应规则为

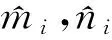
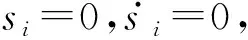
由于si(t)=ei，故

两边积分得

由引理3得到si(t)→0，从而ei(t)→0.

2 数值仿真

定理1与定理2的误差分别见图2与图3.通过观察可得，初始时误差较大，与原点的距离远，但随后误差曲线距离原点越来越近并且逐渐趋于一致.

图2 定理1的系统误差

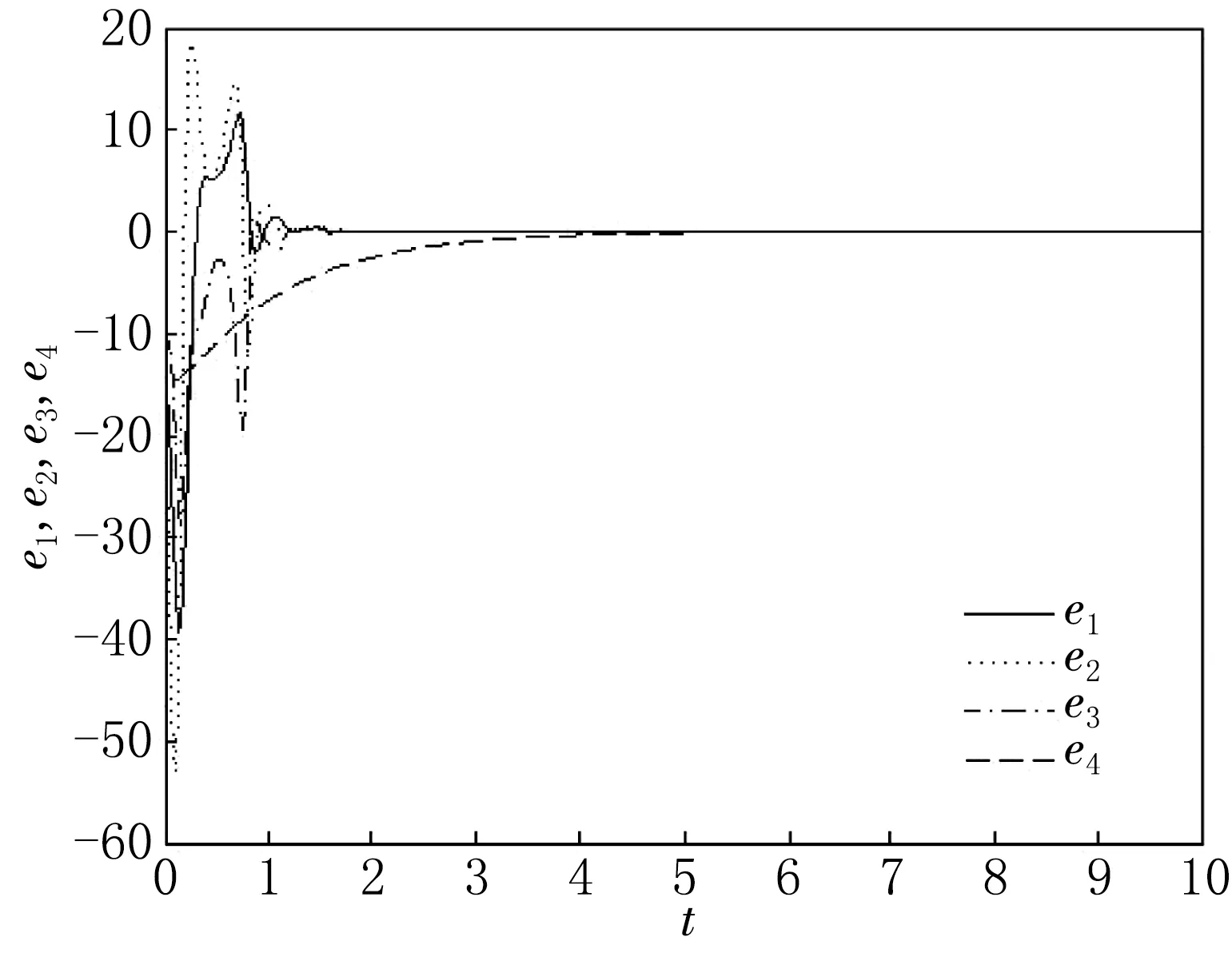
图3 定理2的系统误差

3 结论

通过构造一种整数阶滑模函数和自适应控制规则，对不确定分数阶Like-Bao系统的自适应滑模同步问题进行了研究，得出了系统取得自适应滑模同步的两个充分条件.结论说明在满足一定条件的前提下，不确定分数阶Like-Bao混沌系统的主从系统可取得自适应滑模同步.MATLAB仿真技术也验证了这一结论.