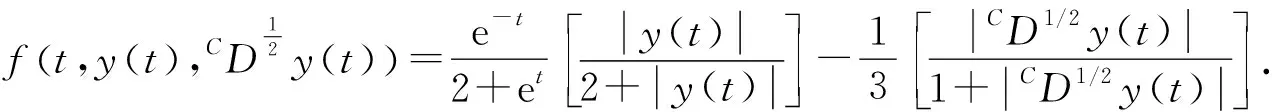具p-Laplacian非局部条件的非线性隐式分数阶微分方程解的存在唯一性
2022-03-26王和香
王 和 香
(喀什大学数学与统计学院,新疆 喀什 844006)
0 引言
作为整数阶微积分的推广,分数阶微积分的起源可以追溯到1695年.由于分数阶构建的模型比整数阶模型更符合实际且方法更多样,使得对分数阶微积分的研究得到迅速发展,并广泛应用于声控、信号处理、多孔介质、电化学等众多领域.
近年来,许多学者进一步研究了具有Caputo导数的分数阶微分方程解的存在性.[1-14]文献[1]利用Banach压缩映射原理讨论了一类具有Caputo导数的隐式分数阶微分方程边值问题
CDαy(t)=f(t,y(t),CDαy(t)),t∈J=[0,T],T>0,0<α≤1;
ay(0)+by(T)=c
解的存在性和稳定性,其中CD是Caputo导数,f:J×R×R→R是连续函数.文献[2]利用Leray-Schauder度理论证明了具有非局部边界条件的隐式分数阶微分方程
CDαu(t)=f(t,u,u′,CDβu,CDαu)
解的存在性,其中1<β<α≤2,函数f连续,CD是Caputo导数.文献[3]利用Banach压缩映射原理和Schauder不动点定理,讨论了含积分边界条件的隐式分数阶微分方程

解的存在唯一性,其中CD是Caputo导数,f:J×R×R,λ∈(0,+∞).受以上文献启发,本文研究一类具p-Laplacian算子的带有非局部条件的非线性隐式分数阶微分方程
(1)

1 预备知识
定义1[4]若α>0,函数u:[0,+∞)→R的Riemann-Liouville分数阶积分定义为
定义2[4]对于α>0,函数u:[0,+∞)→R的Caputo分数阶微分定义为
其中n-1<α≤n,n=[α]+1.
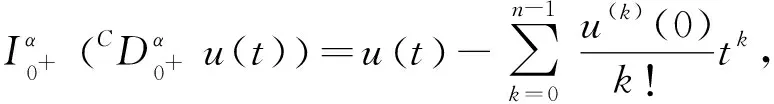

引理3[6](Krasnoselskii不动点定理) 设M为Banach空间上的有界闭凸非空子集,算子A,B满足:①Ax+By∈M,其中x,y∈M;②算子A是紧的且连续;③算子B是压缩映像.则存在z∈M,使得z=Az+Bz.
引理4[7](Arzela-Ascoli定理) 设{f(t)}是定义在α≤t≤β上的一致有界且等度连续的实函数族,则从其中必可选取一个在α≤t≤β上一致收敛的函数列{fn(t)}.
引理5[8]p-Laplacian算子具有以下性质:
(ⅰ) 若1
(ⅱ) 若p>2,|x|,|y|≤M,则|φp(x)-φp(y)|≤(p-1)Mp-2|x-y|.
引理6[9]设0<α≤1,h:[0,T]→R为连续函数,则线性问题
CDαy(t)=h(t),t∈J,y(0)+g(y)=y0

引理7 微分方程(1)等价于如下方程:
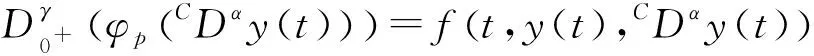
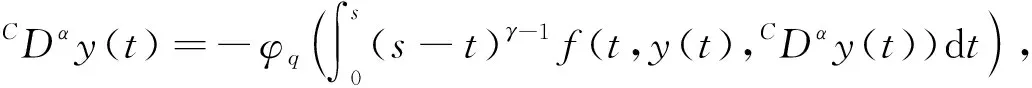
2 主要结论
首先给出以下条件:

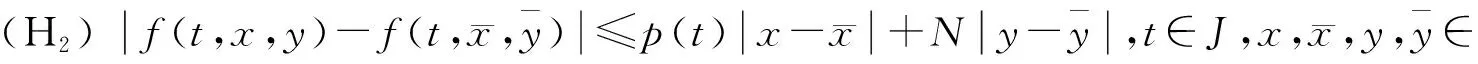
(H3)g:C(J,R+)→R是连续函数,并且满足‖g(x)-g(y)‖≤b‖x-y‖,∀x,y∈C(J,R);
(H4) |f(t,x,y)|≤q(t)|x|+L|y|,t∈J,x,y∈R,q(t)∈C(J,R+),0 证明定义T:C(J,R)→C(J,R), 令 则有 T(BR)⊂BR,BR={y∈C(J,R)|‖y‖∞≤R}. |CDαy(t)|≤|f(t,y(t),CDαy(t))-f(t,0,0)|+|f(t,0,0)|≤p(t)|y(t)|+N|CDαy(t)|+M, 可得 故 则有 任取x,y∈C(J,R),t∈J,有 |CDαx(t)-CDαy(t)|≤|f(t,x(t),CDαx(t))-f(t,y(t),CDαy(t))|≤ 故 由引理5,有 从而 即‖Tx(t)-Ty(t)‖∞≤‖x-y‖∞.由压缩映射原理,算子T有唯一不动点,即微分方程(1)有唯一解. 证明令R≥2(|y0|+G),BR={y∈C(J,R)|‖y‖∞≤R}.定义BR上的算子A,B: 下证Ax(t)等度连续.设t1,t2∈J,x∈BR, 故A(BR)相对紧,由引理4,A是紧的.由引理3可知微分方程(1)至少有一个解. 考虑微分方程 (2) 由定理1,微分方程(2)有唯一解.
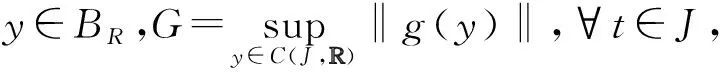
p(t)|x(t)-y(t)|+N|CDαx(t)-CDαy(t)|.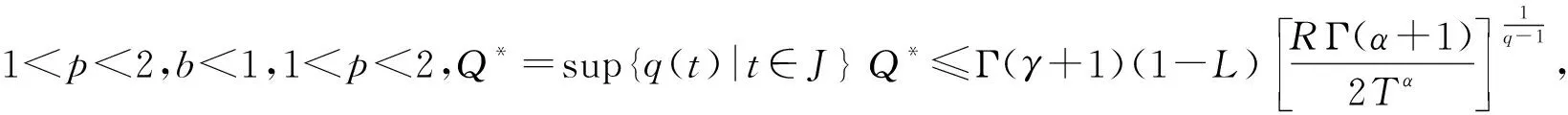
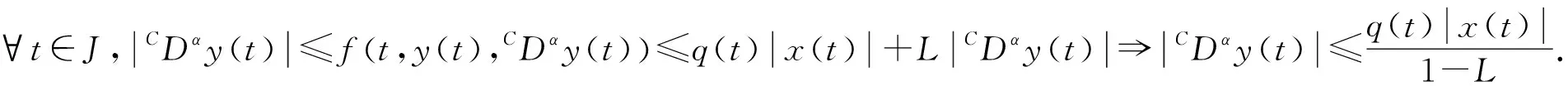
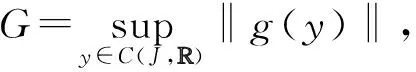
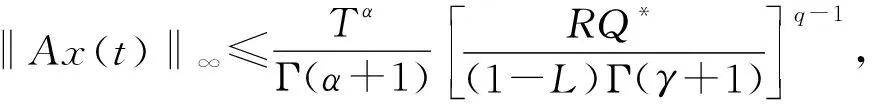
3 例子