3-李2-代数的交换扩张

王春月，张 爽，张庆成

(1.吉林工程技术师范学院应用理学院，吉林 长春 130052；2.吉林建筑大学基础科学部，吉林 长春 130118；3.东北师范大学数学与统计学院，吉林 长春 130024)

1 预备知识

近年来，高阶代数结构备受关注.高阶代数就是将已有数学概念“范畴化”，最简单的一种高阶结构是2-向量空间[1]，即范畴化的向量空间.目前，研究最广泛的一种高阶代数是李2-代数，它是在2004年由Baez等[1]提出的.李2-代数被视为李代数的范畴化.关于李2-代数已经取得了很多重要的结果[2-5].

3-李2-代数作为3-李代数的范畴化以及李2-代数的一种推广是近年来被提出的一类高阶代数.文献[6]详细阐述了3-李2-代数的基本概念及性质，并且证明了3-李2-代数与2-项3-Lie∞代数一一对应，因此3-李2-代数可由2-项3-Lie∞代数给出.文献[7]解决了3-李2-代数的构造问题，利用3-Leibniz代数和Rota-Baxter 3-李代数构造了3-李2-代数.本文主要研究3-李2-代数的交换扩张问题.本文所有的线性空间和代数均为数域K上的.

定义1[6]3-李2-代数L=(L1，L0，d，l3，l5)包括：

(ⅱ) 完全反对称三线性映射l3：Li×Lj×Lk→Li+l+k(0≤i+j+k≤1).

(ⅲ) 多重线性映射l5：(L0∧L0)⊗(L0∧L0∧L0)→L1.

(ⅳ) 对于任意的x，y，xi∈L0(i=1，…，5)，a，b，c∈L1，下列等式成立：

dl3(x，y，a)=l3(x，y，da)；

(1)

l3(a，b，c)=0，l3(a，b，x)=0；

(2)

l3(da，b，x)=l3(a，db，x)；

(3)

dl5(x1，x2，x3，x4，x5)=-l3(x1，x2，l3(x3，x4，x5))+l3(x3，l3(x1，x2，x4)，x5)+
l3(l3(x1，x2，x3)，x4，x5)+l3(x3，x4，l3(x1，x2，x5))；

(4)

l5(da，x2，x3，x4，x5)=-l3(a，x2，l3(x3，x4，x5))+l3(x3，l3(a，x2，x4)，x5)+
l3(l3(a，x2，x3)，x4，x5)+l3(x3，x4，l3(a，x2，x5))；

(5)

l5(x1，x2，da，x4，x5)=-l3(x1，x2，l3(a，x4，x5))+l3(a，l3(x1，x2，x4)，x5)+
l3(l3(x1，x2，a)，x4，x5)+l3(a，x4，l3(x1，x2，x5))；

(6)

l3(l5(x1，x2，x3，x4，x5)，x6，x7)+l3(x5，l5(x1，x2，x3，x4，x6)，x7)+
l3(x1，x2，l5(x3，x4，x5，x6，x7))+l3(x5，x6，l5(x1，x2，x3，x4，x7))+
l5(x1，x2，l3(x3，x4，x5)，x6，x7)+l5(x1，x2，x5，l3(x3，x4，x6)，x7)+
l5(x1，x2，x5，x6，l3(x3，x4，x7))=l3(x3，x4，l5(x1，x2，x5，x6，x7))+
l5(l3(x1，x2，x3)，x4，x5，x6，x7)+l5(x3，l3(x1，x2，x4)，x5，x6，x7)+
l5(x3，x4，l3(x1，x2，x5)，x6，x7)+l5(x3，x4，x5，l3(x1，x2，x6)，x7)+
l5(x1，x2，x3，x4，l3(x5，x6，x7))+l5(x3，x4，x5，x6，l3(x1，x2，x7)).

(7)

若d=0(l5=0)，则称3-李2-代数为简单的(严格的).

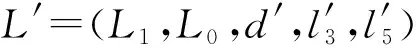
F0∘d=d′∘F1，

(8)

(9)

(10)

(11)

则称F=(F0，F1，F2)：L→L′是3-李2-代数同态.

若F2=0，则称F是严格同态.

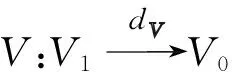
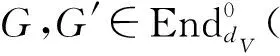
定理1[8](End(V)，δ，l2)是严格李2-代数.

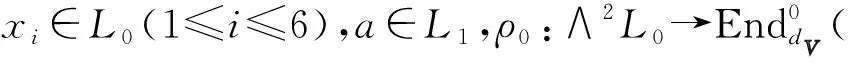
δρ1(a，x)=ρ0(da，x)，

(12)

dVρ2(x1，x2，x3，x4)=ρ0(x3，l3(x1，x2，x4))+ρ0(l3(x1，x2，x3)，x4)+
ρ0(x3，x4)ρ0(x1，x2)-ρ0(x1，x2)ρ0(x3，x4)，

(13)

ρ2(da，x2，x3，x4)=ρ1(x3，l3(a，x2，x4))+ρ1(l3(a，x2，x3)，x4)+
ρ0(x3，x4)ρ1(a，x2)-ρ1(a，x2)ρ0(x3，x4)，

(14)

ρ2(x1，x2，da，x3)=ρ1(a，l3(x1，x2，x3))+ρ1(l3(x1，x2，a)，x3)+
ρ1(a，x3)ρ0(x1，x2)-ρ0(x1，x2)ρ0(a，x3)，

(15)

ρ1(l5(x1，x2，x3，x4，x5)，x6)+ρ1(x5(l5(x1，x2，x3，x4，x6)))+
ρ0(x1，x2)ρ2(x3，x4，x5，x6)+ρ0(x5，x6)ρ2(x1，x2，x3，x4)+
ρ2(x1，x2，l3(x3，x4，x5)，x6)+ρ2(x1，x2，x5，l3(x3，x4，x6))+
ρ2(x1，x2，x5，x6)ρ0(x3，x4)=ρ0(x3，x4)ρ2(x1，x2，x5，x6)+
ρ2(l3(x1，x2，x3)，x4，x5，x6)+ρ2(x3，l3(x1，x2，x4)，x5，x6)+
ρ2(x3，x4，l3(x1，x2，x5)，x6)+ρ2(x3，x5，l3(x1，x2，x6))+
ρ2(x1，x2，x3，x4)ρ0(x5，x6)+ρ2(x3，x4，x5，x6)ρ0(x1，x2).

(16)

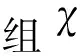
(17)

(18)

(19)

(20)

(21)

(22)

2 3-李2-代数的交换扩张

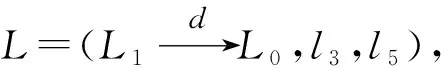
Im(i)=Ker(p)，

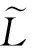
定理2 在上述条件下，线性映射ρ=(ρ0，ρ1，ρ2)是L在L′上的表示.

证明由定义1、定义2和定义3直接计算可得.

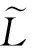
证明只需证明定义4的(3)式，其他等式类似可得.任取xi∈L0(1≤i≤5)，由定义1可得，