截渗墙作用下滨海地下水渗流与排泄特征❋

2022-03-26高明鹏郑西来郑天元常钦鹏方运海

中国海洋大学学报(自然科学版) 2022年4期

高明鹏，郑西来❋❋，郑天元，常钦鹏，方运海，张博

(1.中国海洋大学环境科学与工程学院，山东青岛 266100；2.山东省海洋环境地质工程重点实验室，山东青岛 266100；3.中国海洋大学工程学院，山东青岛 266100)

世界上约有70%的人口居住在沿海地区，在这些地区，地下水是主要的供水水源，因此地下水的水质对当地居民的生活至关重要[1-2]。在滨海含水层中，地下水在水力梯度的驱动下向海洋排泄，这是陆地向海洋进行物质输送的一个重要过程[3]。在许多沿海地区，地下水排泄量等同甚至数倍于地表径流量[4]。地下水的排泄是全球水循环的一个重要组成部分，同时也与滨海含水层中地下水的水质有着密切的联系[5]。在排泄过程中，地下水中的溶解物质(营养盐、金属元素等)会被携带入海，从而避免了这些物质的积累对含水层和地下水的污染[6]。Zhou等[7]评估了全球不同沿海地区的地下淡水排泄量，发现相比于干旱的中纬度地区，热带地区地下淡水排泄量更大。据此，他们认为干旱的中纬度地区的含水层更容易受到盐碱化的影响。

为满足沿海地区居民用水和工农业发展的需要，大量的地下水被抽取。同时，气候变化导致的海平面上升现象愈发严重。这使得地下水位相对海平面下降，海水-地下水界面向陆地方向移动，这种现象被称为海水入侵(见图1(a))[8-9]。海水入侵会造成地下水质恶化、地下设备腐蚀、农作物减产等危害。为防治海水入侵，国内外研究者提出了许多方法，如抽提咸水、人工回灌、优化抽水井布设模式和修筑地下物理帷幕等[10]。其中地下物理帷幕以其防治效率高、运行及维护成本低等优点而在世界范围内得到了广泛的应用[11]。常见的地下物理帷幕按照使用材料和修建位置可分为三种主要类型[12]：(1)由半透水材料组成，垂直贯穿整个含水层的半渗透物理帷幕，这种帷幕在实际工程中已经很少使用(见图1(b))[13]；(2)由不透水材料组成，修建在含水层隔水底板上并具有一定高度，上段开口以允许地下水向海洋排泄的地下坝(见图1(c))；(3)由不透水材料组成，从地表开始修建并穿透含水层到一定深度，下端开口以允许地下水流通过的截渗墙(见图1(d))。

图1 海水入侵和地下物理帷幕示意图

各类型的地下物理帷幕中，截渗墙防治海水入侵的有效性已经得到了充分的证明[14-16]。目前，截渗墙的修建对地下水环境的影响正引发研究者的关注。Ishida等[17]综述了墙体建设的基本问题、设计指标，并提出了与地下水循环利用有关的一系列问题，如盐渍化、硝酸盐污染和区域地下水流场改变等。在国内，大沽河流域截渗墙的修建使上游地下水中氯离子含量明显减少，但也在极大程度上限制了地下水向海排泄，建成后10年左右的排泄量仅相当于建成前一天的排泄量[18-19]。刘金玉[20]研究表明，三涧堡地下截渗墙的建成使上游地下水位抬升超过6 m，基本解决了当地居民用水需求；但由于前期设计时未考虑排泄的问题，导致当地耕地减产面积达1/10。Senthilkumar等[21]对印度南部某流域进行了数值模拟，模拟结果表明，当地截渗墙建成后，上游地下水位将升高10～30 cm，而下游地下水位将降低10～20 cm。Chang等[22]通过室内试验和数值模拟探究了地下截渗墙对淡水排泄的影响，发现具有最小有效高度的墙体可以有效防治海水入侵，同时保持最大的地下水排泄量。

总的来说，以往的研究已经证明，截渗墙的建设对地下水的排泄存在一定的影响，然而目前仍然难以确定两者的定量关系。存在的问题主要表现在以下两点：(1)评价指标单一，未考虑排泄过程中地下水渗流速度的变化；(2)通常只研究稳态的地下水排泄量，而实际上排泄量会随时间发生变化。因此，本研究以截渗墙为研究对象，定量刻画了截渗墙条件下地下水渗流和排泄的变化特征。

1 地下水数值模型建立与求解

1.1 定解条件

本研究考虑截渗墙建设前后的海水入侵过程，为简化这一问题，我们假设：(1)含水层为潜水含水层，均质、各向同性；(2)含水层完全饱水；(3)流体和固体都不可压缩；(4)流体密度仅取决于盐的浓度。在上述假设基础上，本文按图2所示建立概念模型。模拟区域为一个(300×30)m2的二维纵向垂直截面。模型的顶部和底部设置为Neumann无流动边界，没有任何流体的流动和物质的运输；左侧为内陆地下水的定水头边界和Dirichlet质量边界，水头值为28.5 m(hf)，浓度值为0 g/L(C0)；右侧为海水的定水头边界和Dirichlet质量边界，水头值为29.4 m(hs)，浓度值为36 g/L(Cs)。截渗墙厚度设置为1 m，墙体内没有流体和物质的运移。

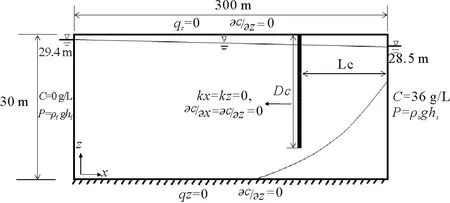
图2 场地尺度数值模拟的模型设置

1.2 数值解法

在上述定解条件的基础上建立数值模型。有限差分模型SEAWAT-2000[23]被用于求解数值模型中的变密度地下水流和溶质运移方程，从而进行海水入侵过程的模拟。

使用预处理共轭梯度(PCG)方法对流量方程进行处理。广义共轭梯度(GCG)作为溶质运移方程的色散项和源项，改进特征方法被用于求解方程的平流项。使用Matlab软件(Mathworks, I., 2018a)进行模型数据的转换、计算和可视化等后处理工作。基于以往场地尺度研究中所常用的含水层参数，我们设置并保持含水层水力梯度(J)为3‰，孔隙度(n)为0.4，水力传导率(K)设置为0.000 6 m/s，纵向弥散度(αL)设置为1 m，横向弥散度(αT)为纵向弥散度的1/10[24-27]。模型区域被Δx×Δz=1 m×1 m尺寸的矩形单元离散化为9 000个网格。网格划分方案满足Péclet指标，因此可以认为所建立的模型具有足够的数值稳定性[28]。Péclet指标Pem定义如下：

(1)

式中：Δx为沿x轴方向的网格尺寸；αL为含水层中纵向弥散度。

时间步长设为1 d。模拟的应力期设为3 000 d，这一时间长度足够模拟的所有案例达到稳定状态。地下水排泄量通过模型中的Zone Budget模块计算，设置模拟区域左侧第二列网格为流量计算区。根据水量平衡原理，应力期内从流量计算区流入含水层的水量即为地下水的排泄量。使用模型中的Velocity模块计算地下水的流速。模型中截渗墙的模拟通过设置特定区域为非活动单元来实现。截渗墙深度的参考值为24 m，与海洋边界距离的参考值为60 m，在此基础上采用控制变量的方法研究截渗墙结构对地下水渗流和排泄的影响，共进行17组模拟。主要的模拟方案和模型参数如表1所示。

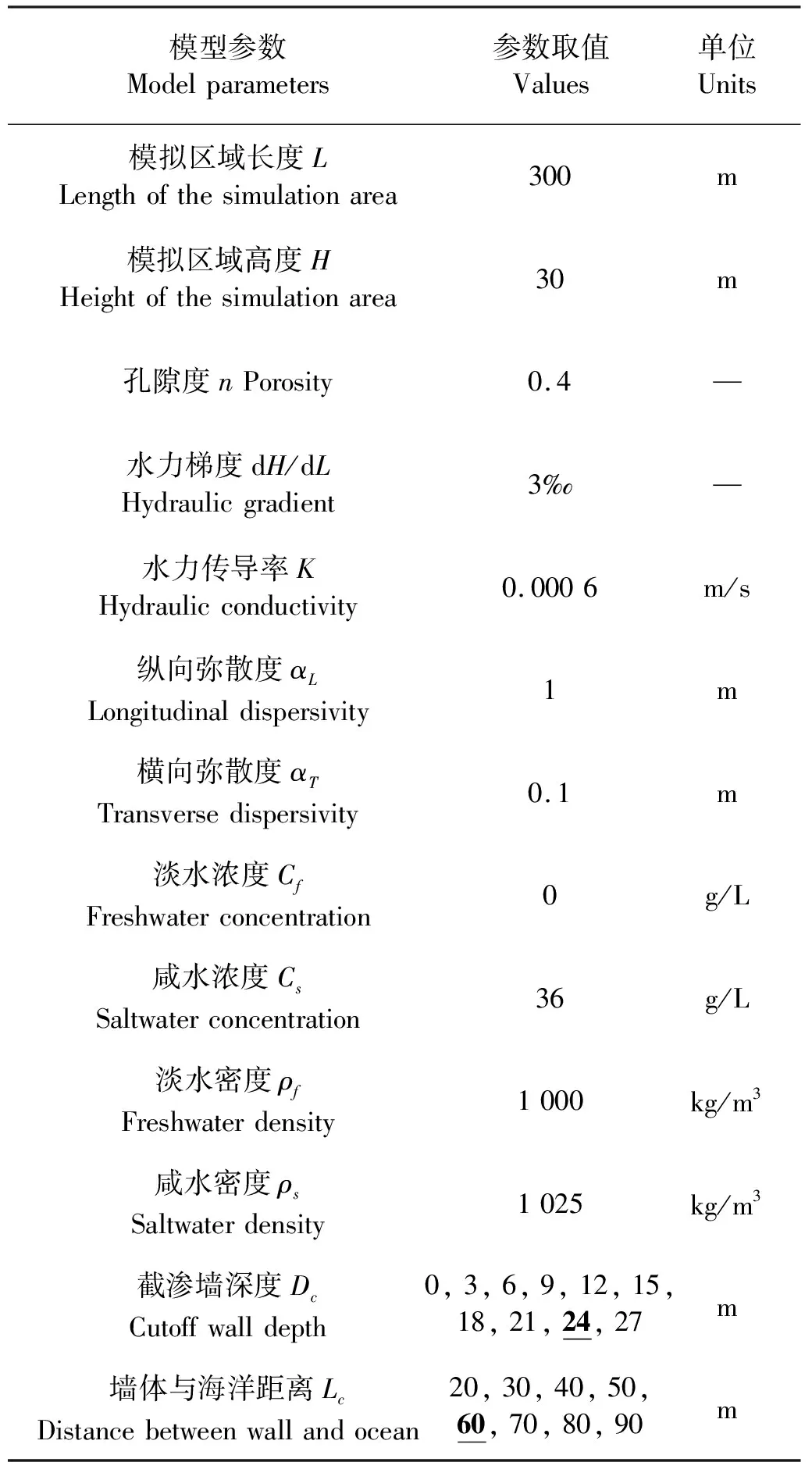
表1 数值模拟参数

1.3 评价指标

使用地下水相对流速(V)和相对排泄量(Q)来评价截渗墙对含水层中地下水渗流和排泄的影响。其中，地下水相对流速包括相对最大流速(Vmax)和相对平均流速(Vmean)。为便于描述和对比，上述指标均设置为无量纲变量，定义如下：

(2)

(3)

(4)

式中：Q0、V0和V0′分别代表无墙条件下的地下淡水排泄量、含水层内局部最大流速和地下水平均流速；Qt、Vt和Vt′分别代表截渗墙建设后的地下淡水排泄量、含水层内局部最大流速和地下水平均流速。

2 结果与讨论

2.1 无墙和有墙条件下地下水渗流和排泄特征

模拟了无墙和有墙条件下的海水入侵过程以探究截渗墙的建设对地下水渗流和排泄的影响，结果如图3所示。图中白色箭头的方向代表流速方向，箭头长度代表流速大小(下文中相同)。如图3(a)所示，无墙条件下含水层中稳态咸水楔的长度为170 m(以海水浓度的50%浓度等值线为准[29-30])，由于楔内咸水的高浓度、高密度，整个咸水楔成为一个地下淡水无法通过的低流速区(流速值小于1×10-6m/s)。因此，含水层中的地下淡水流动至咸水楔时会沿着咸淡水界面向右上方的排泄口运动。这一过程中，随着与海洋边界距离的减小，咸水楔厚度越来越大，淡水的排泄空间逐渐被压缩，所以淡水的流速逐渐增大，并在含水层的排水口(咸水楔上方)处达到最大值。此外，由于低流速区域内咸水的流速方向与含水层内淡水流速方向相反，二者达到一个动态稳定的状态。因此在含水层垂直方向上，越靠近咸水楔，淡水流速越小，速度最小的区域位于咸淡水过渡带处。

截渗墙建设后，地下水的流动受阻。因此，含水层内的地下水流速显著降低，截渗墙顶部陆侧区域降低得尤为明显(见图3(b))。然而，截渗墙底部及其右侧的狭窄空间出现了新的高流速区(流速值大于1×10-5m/s)。这是由于被截渗墙阻挡的地下水流动方向发生改变，并集中在截渗墙底部进行排泄。与此同时，通过截渗墙底部的地下水还需通过墙体与咸水楔之间的区域才能向海洋排泄，狭窄的排泄空间导致了高流速区的产生。与截渗墙建设前相比，此时含水层排泄口处原本的高流速区面积减小了16%。此外，截渗墙下方的咸水楔内部出现了流速较大的区域，这导致咸水楔趾部形状出现波动。截渗墙条件下地下水渗流特征和排泄路径的改变使咸水楔长度从170 m缩短至60 m，但墙体下游咸淡水过渡带的面积明显增加。

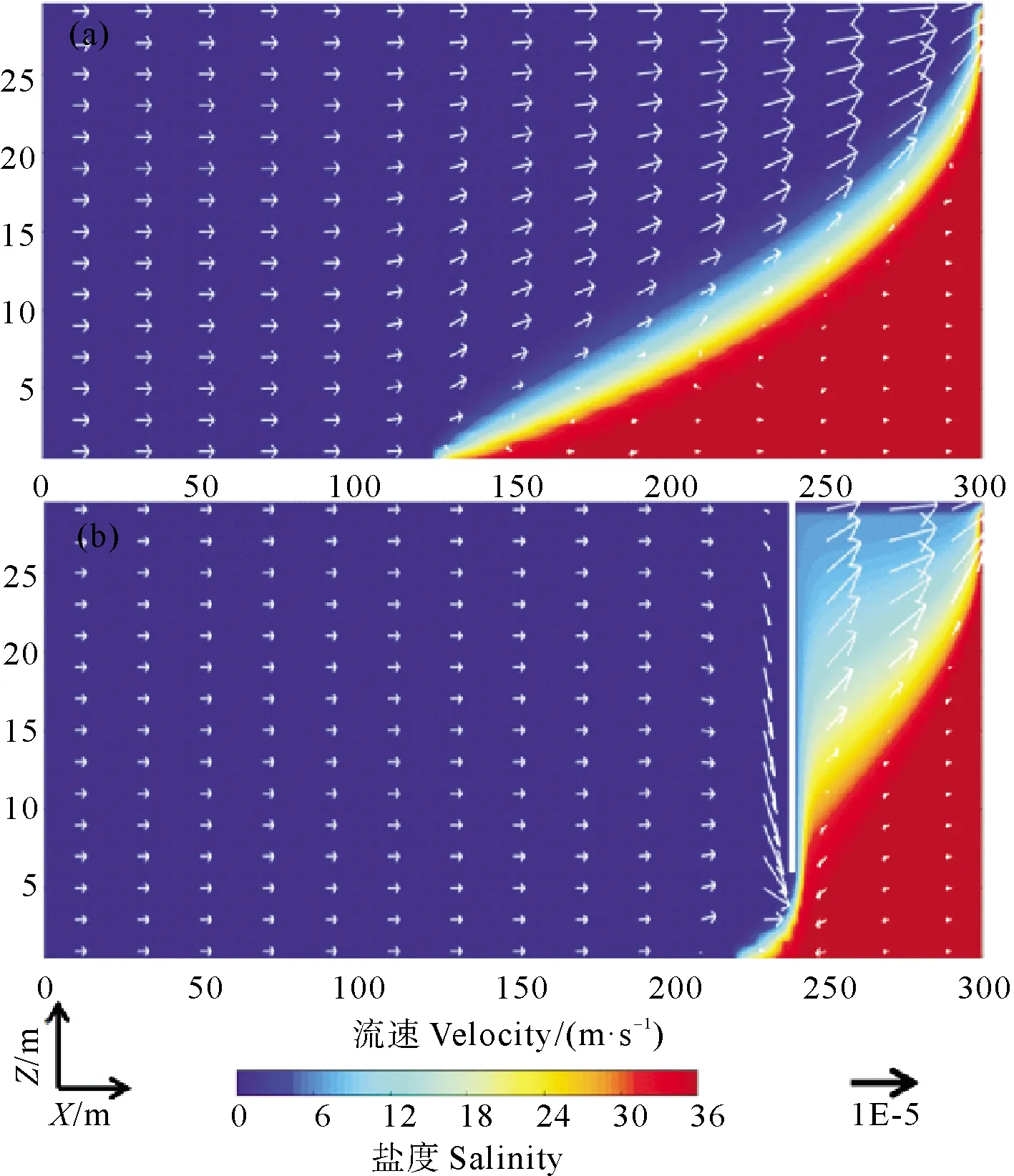
图3 无墙(a)和有墙(b)条件下地下水渗流特征

墙体建设前后地下水相对排泄量随时间的变化如图4所示。在无墙条件下，相对排泄量在极短时间内(15 d)迅速上升并达到稳定。在15～3 000 d期间，咸水楔持续向内陆延伸，长度及厚度不断增加，地下水排泄空间逐渐被压缩。但由于含水层厚度较大，地下水排泄空间的缩小会带来流速的增加，因此地下水排泄量并没有发生变化。也就是说，在无墙条件下，咸水楔的形态对地下水排泄量不会产生影响。截渗墙建设后，地下水相对排泄量增速变慢，在32 d时增加至84.5%，之后开始缓慢下降，在404 d时降至59.4%并达到稳定。此时截渗墙深度为含水层厚度的80%，这意味着地下水排泄空间被极大地压缩。因此，尽管截渗墙底部地下水流速显著增大，但含水层整体的地下水流速降低，相对排泄量减小。截渗墙安装32 d后相对排泄量开始降低的原因在于，此时咸水楔已经逼近截渗墙，高浓度咸水开始逐渐占据截渗墙下方的地下水排泄通道。不同于截渗墙安装前，此时地下水的排泄空间已经很狭窄(仅为含水层厚度的20%)，随着咸水的入侵，流速的增加已经不能抵消排泄空间进一步缩小带来的影响，因此相对排泄量开始降低。

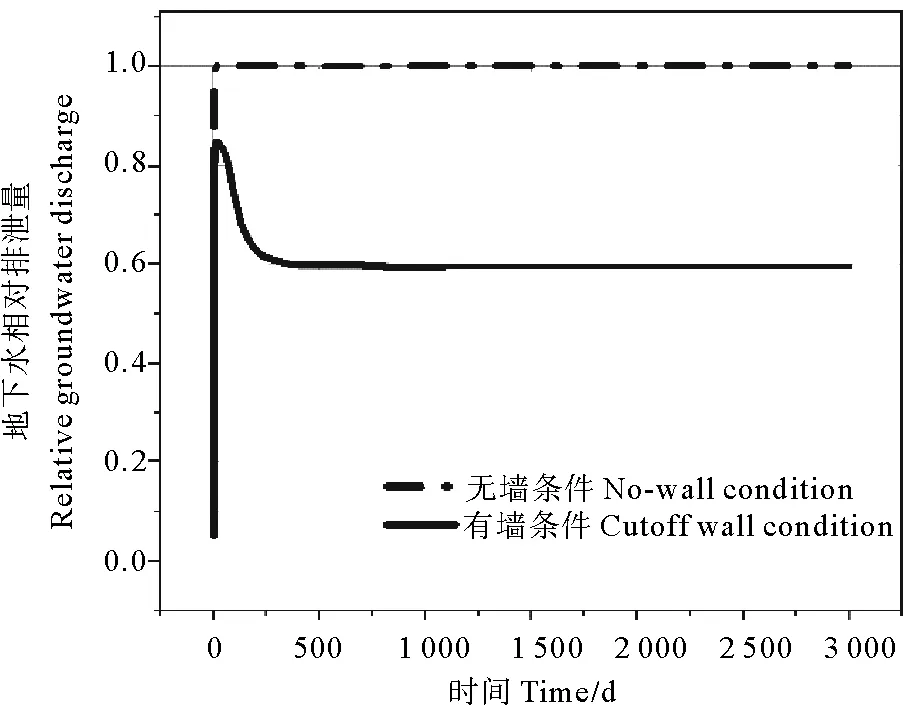
图4 无墙和有墙条件下地下水相对排泄量随时间的变化

2.2 截渗墙深度对地下水渗流和排泄的影响

墙体距海洋边界60 m，深度为18～27 m时，地下水的渗流特征如图5所示。随着墙深的增加，咸水楔长度逐渐缩短，意味着截渗墙防治海水入侵的效果增强；与此同时，墙体右侧咸淡水过渡带的面积逐渐增大。此外，截渗墙上游含水层内的地下水流速明显降低。墙深Dc=18 m时，上游含水层中地下水流速值约是咸水楔内高浓度咸水的3～4倍；而在墙深Dc=27 m时，上游含水层内的地下水流速值与咸水楔内的高浓度咸水大致相当。随着墙深的增加，含水层排水口处的高流速区域的面积减小，这意味着截渗墙深度的增加不仅会降低墙体上游地下水的流速，还会影响墙体下游的排泄过程。

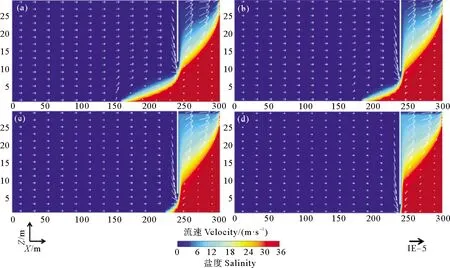
图5 墙深为18 m(a)、21 m(b)、24 m(c)和27 m(d)时的地下水渗流特征

上述4组墙深条件下地下水相对排泄量随时间的变化如图6所示。与图4中描述的趋势相同，4组案例中地下水相对排泄量均在短时间内迅速上升至最大值，然后缓慢下降直至达到稳定。相比之下，截渗墙越深，地下水相对排泄量能够达到的最大值越小，且之后的下降幅度越大。在墙深Dc为18、21、24和27 m时，地下水相对排泄量达到的最大值分别为92.3%、88.9%、84.5%和76.4%，之后分别降低了11.5%、17.7%、25.1%和29.9%，达到稳定状态。总的来说，截渗墙深度的增加会显著降低含水层中地下水的流速和排泄量。

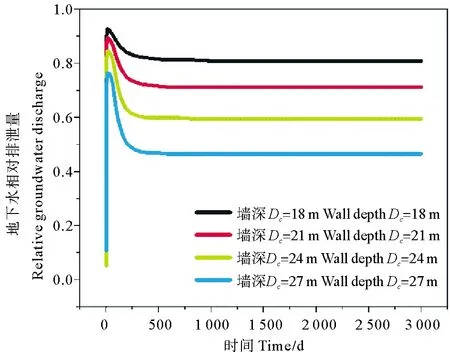
图6 不同墙深条件下地下水相对排泄量随时间的变化

为定量研究墙体深度的变化对地下水渗流和排泄的影响，本文在上述4组案例的基础上共进行了10组不同截渗墙深度的模拟。如图7(a)所示，随着墙深的增加，含水层中地下水相对平均流速显著降低，且降低速率逐渐增大。这是由于入侵的咸水楔会占据截渗墙底部空间，与截渗墙同时压缩地下水的排泄通道，从而导致上游含水层中的地下水无法及时排泄。墙深从0 m增加到18 m，相对平均流速仅降低了约19%；而当墙深Dc>18 m时，深度每增加3 m，相对平均流速就降低约11%，在Dc=27 m时，相对平均流速已降至49%。截渗墙越深，地下水的排泄通道越窄，因此地下水相对平均流速的降低越显著。

截渗墙条件下含水层中存在两个地下水的高流速区(截渗墙底部和含水层排水口处)，而随着截渗墙深度的变化，这两个区域的流速值也会相应发生改变。在墙深Dc<18 m时，同无墙条件下一样，含水层中的最大流速值仍出现在含水层排水口处，但相对流速值从100%降低至76%。由于截渗墙会阻碍并改变地下水的排泄路径，即使在墙深很小(Dc=3 m)时，相对最大流速值仍迅速降低了17%。相比之下，此时的相对平均流速值仅降低了0.3%，也就是说，深度较小的截渗墙对含水层中地下水平均流速的影响很小，但会显著改变局部的最大流速值。在墙深Dc≥18 m时，最大流速值出现的位置不再是含水层排水口处，而是转移到截渗墙底部，且随着墙深的增加，其数值逐渐增大并趋于稳定。这是由于在截渗墙深度增加的过程中，由于墙体对地下水排泄的阻挡程度越来越高，含水层排水口处的流速值逐渐减小；而由于排泄空间的压缩，通过截渗墙底部的地下水逐渐被加速，此区域也成为含水层中新的最大流速区。

地下水相对排泄量随墙深的变化(见图7(b))与相对平均流速的变化趋势相似。墙深从0 m增加至15 m时，相对排泄量降低了11%；之后深度每增加3 m，相对排泄量依次降低8%、10%、12%和13%，在墙深Dc=27 m时，相对排泄量仅为46%。这意味着只有深度较大(含水层厚度的50%以上)的截渗墙才会明显降低地下水排泄量。总的来说，在截渗墙深度较大时，地下水排泄量和平均流速对深度的变化更加敏感。

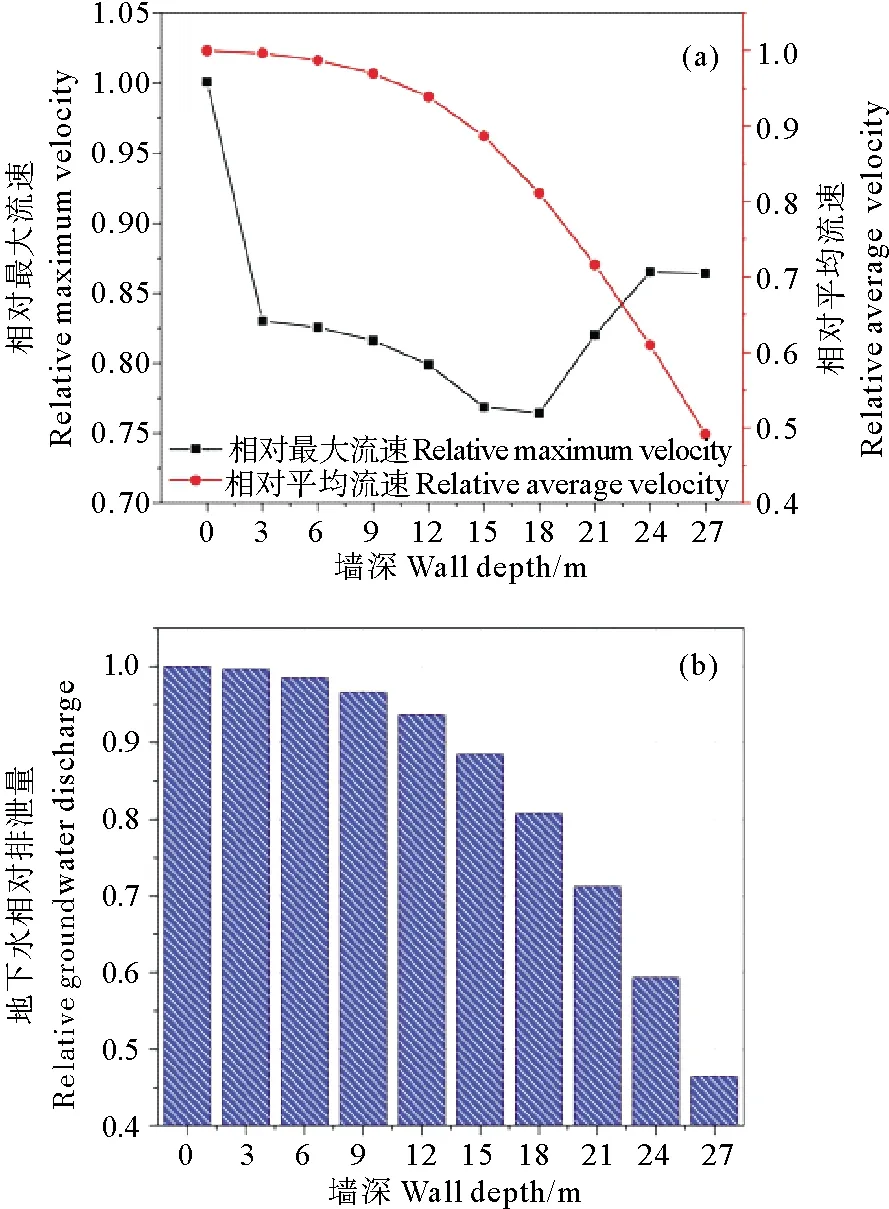
图7 稳态地下水相对流速(a)及相对排泄量(b)随墙深的变化

上述研究结果可以为实际生活中海水入侵的防治和地下水资源的保护提供一定的参考。以青岛大沽河水源地的截渗工程为例，该截渗墙底部位于含水层隔水底板之上，顶部直达地表[18]。在这种深度条件下，截渗墙虽然可以有效防止海水入侵含水层，但同时也会阻碍地下淡水的渗流和排泄，造成污染物积累、土壤盐渍化等危害[17]。因此，在实际工程设计中，应注意保留墙体下方地下水的排泄空间。如图7(b)所示，在墙体深度为21、24和27 m时，地下水相对排泄量分别为71.2%、59.4%和46.5%。也就是说，若将截渗墙深度设计为含水层厚度的70%～90%，这样不仅可以保持良好的海水入侵防治效果，同时减小了墙体对地下水渗流和排泄的阻挡作用，从而有利于地下水环境的保护。此外，截渗墙深度的减小还可以有效降低建设成本。

2.3 截渗墙位置对地下水渗流和排泄的影响

截渗墙建设位置的不同会导致墙体与海洋边界的距离发生变化，从而改变咸水楔的形态。墙深为24 m，墙体距离海洋边界20～80 m时的模拟结果如图8所示。从图中可以看到，截渗墙位置越靠近海洋边界，即二者之间距离越小，咸水楔长度越短，墙体防治海水入侵的效果越好；与此同时，截渗墙右侧咸水楔高度越来越大。截渗墙位置的变化同样会影响地下水的渗流和排泄过程。随着截渗墙与海洋边界距离减小，墙体下游地下水的排泄空间逐渐减小；而咸水楔的高度的增加进一步压缩了地下水的排泄通道，因此截渗墙右侧的高流速带逐渐延长。此外，截渗墙向海洋边界移动过程中，上游含水层中的地下水流速略微降低；同时，咸水楔内高浓度咸水的流速也有所增大。

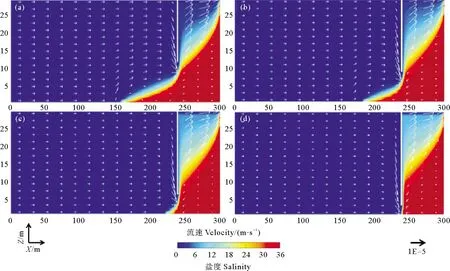
图8 截渗墙距离海洋边界80 m(a)、60 m(b)、40 m(c)和20 m(d)时的地下水渗流特征

在上述4组墙体位置条件下，地下水相对排泄量随时间的变化如图9所示。在截渗墙与海洋边界距离Lc为80、60和40和20 m时，地下水相对排泄量达到的最大值分别为84.9%、84.5%、82.7%和68.3%，之后分别降低了20.3%、25.1%、28.8%和19.6%,达到稳定状态，所需时间分别为697.7、403.8、233.7和78.3 d。截渗墙与海洋边界距离近时，咸水楔会更快地入侵到截渗墙下方，因此地下水相对排泄量开始下降的时间更早，也更快地达到稳定。

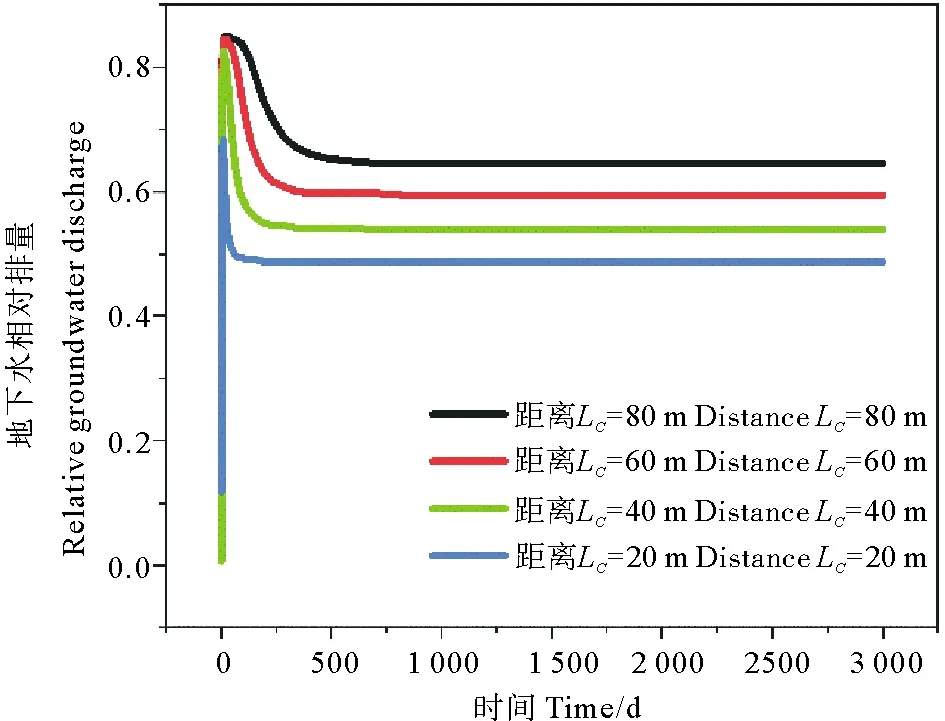
图9 不同墙体位置条件下地下水相对排泄量随时间的变化

图10(a)展示了地下水平均和最大流速值随截渗墙位置的变化。随着墙体逐渐远离海洋边界，地下水相对平均流速从距离Lc=20 m时的47.2%，几乎线性增加到Lc=90 m时的69.8%。这是因为截渗墙离海洋边界越远，墙体下游的咸水楔高度越小，这意味着地下水的排泄路径更短，因此更有利于地下水的排泄。此外，从图8中可以看出，墙体与海洋边界之间是地下水流速较大的区域，因此二者之间距离远意味着这一区域的面积大，这也在一定程度上提高了地下水的平均流速。与平均流速相比，地下水最大流速值随截渗墙位置的变化并没有呈现出一定的规律性。但由于截渗墙深度保持在24 m，最大流速值出现的位置始终在截渗墙底部。

随着截渗墙与海洋边界距离的增加，地下水相对排泄量从Lc=20 m时的48.7%持续增大至Lc=90 m的66.8%，且增幅较为稳定(见图10(b))。截渗墙与海洋边界的距离从20 m增加至50 m和从50 m增加至80 m的过程中，含水层中地下水相对平均流速分别增加了12%和8.3%，地下水相对排泄量增加了8.1%和7.7%。这说明截渗墙与海洋边界距离近时，地下水排泄量与平均流速对截渗墙位置的变化更敏感。但相比于深度变化，这种敏感性的差别并不明显。

由以上分析可以推知，在实际截渗工程当中，若条件允许，可以使截渗墙的建设位置尽可能靠近海岸带。这样虽然会导致截渗墙对地下水渗流和排泄的阻碍程度有所提高，但可以显著减小墙体下游的咸水面积，同时增加墙体上游含水层的储水空间(见图8)，有利于地下淡水资源的储存和开发。