基于动量因子DD-LMS算法在高速相干接收机中的应用

龚 闯，刘志强，2，陆 叶，周 鹏，武康康，李传起，3

(1.广西师范大学 电子工程学院， 广西 桂林 541004；2.中国电子科技集团公司 第三十四研究所， 广西 桂林 541004； 3.南宁师范大学 物理与电子学院， 广西 南宁 530001)

在单模光纤中，基模的群速度与频率相关，脉冲不同的频谱分量以略微不同的群速度传输，导致光脉冲在传输过程中展宽从而引起码间串扰(intersymbol interference,ISI)，影响信号的传输距离和传输质量。

实际光通信系统中，受外界因素影响，色散信道模型并不是恒定的，一般会在接收机数字信号处理(digital signal processing, DSP)模块中加入采用自适应的思想设计的均衡滤波器用于估计变化参数。重叠-保留法采用光纤色散理想期望传输函数[1]对色度色散(chromatic dispersion,CD)进行补偿，将信号分块，变换到频域上，截断分块后的两端部分序列，对残余色散进行补偿，计算复杂度大，同时无法完全消除其他因素对信号的扰动。恒模算法(constant modulus algorithm，CMA)及其改进类算法在信道变化剧烈时，稳态误差较大，收敛速度较慢，一般迭代次数需大于8 000次[2-6]，难以满足实际传输系统的需求。基于机器学习的色散补偿模块，利用神经网络[7-9]、支持向量机[10-13](support vector machine,SVM)等技术训练相应的映射网络，在一定程度上能估计出信道模型，但训练计算量大、系统延时高，一般需对数据样本遍历150 000 次左右，无法适应高速光系统。

本文构建基于动量因子的判决引导的最小均方(momentum decision-directed least means-square，MDD-LMS)算法，从理论上论证了动量因子对此算法收敛性的影响，推导了动量因子与迭代步长之间的关系。结果表明，在基于OptiSystem的56 Gbaud双偏振非归零正交相移键控(non return zero-quadrature phase shift keying，NRZ-QPSK)相干光传输系统中，相比于其他盲均衡算法，MDD-LMS收敛速度明显加快；在面对色散常数变化时，此算法具有良好的均衡性能。

1 算法结构

在采用QPSK调制格式的光纤传输系统中，通过相干接收机前端完成光电转换、模数转换、正交归一化、时钟恢复等步骤后，在用于补偿光纤线性损伤的接收机中进行数字信号处理(流程如图1所示)。

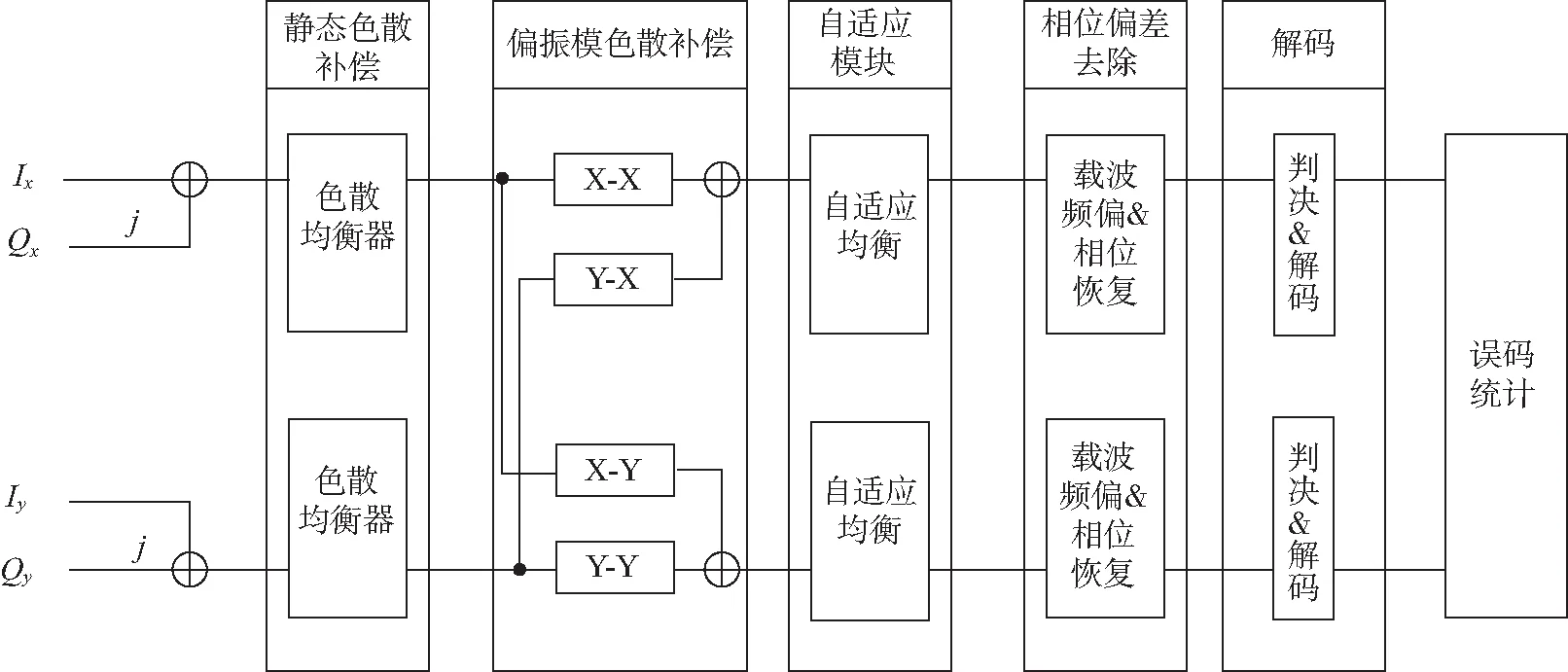
图1 数字相干光接收机中DSP流程Fig. 1 DSP flow chart in digital coherent optical receiver

在数字相干光接收机中，CD对光纤通信系统的影响被建模[12]为

H(ω,z)=exp[-jK(ωT)2]，

(1)

(2)

式(1)和式(2)中：ω为等效基带信号的角频率，T为信号采样周期,D为光纤色度色散常数,λ为传输波长，z为传输距离，c为光速。

1.1 时域色散补偿均衡器

高速光通信系统一般采用有限长单位冲激响应(finite impulse response,FIR)的滤波器结构进行补偿。补偿可在频域或时域进行。将式(1)进行傅里叶反变换，可得时域均衡器(time domain equalizer,TDE)的冲激响应为

(3)

考虑到对信号的采样频率需满足奈奎斯特抽样定理，可得FIR滤波器抽头系数为

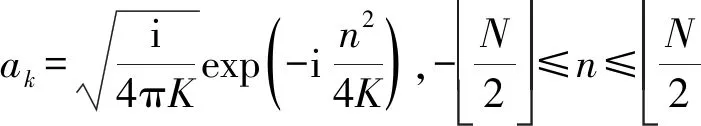
(4)

N=2[2πK]+1。

对于色散常数恒定光纤模型，时域色散均衡器的抽头权重模值恒定，其实部和虚部呈周期性变化。实际应用中，FIR滤波器由于截断效应，导致经过TDE后的信号中依然会存在一定值的残余色散，一般通过后续自适应均衡算法去除。

1.2 MDD-LMS算法理论与实现

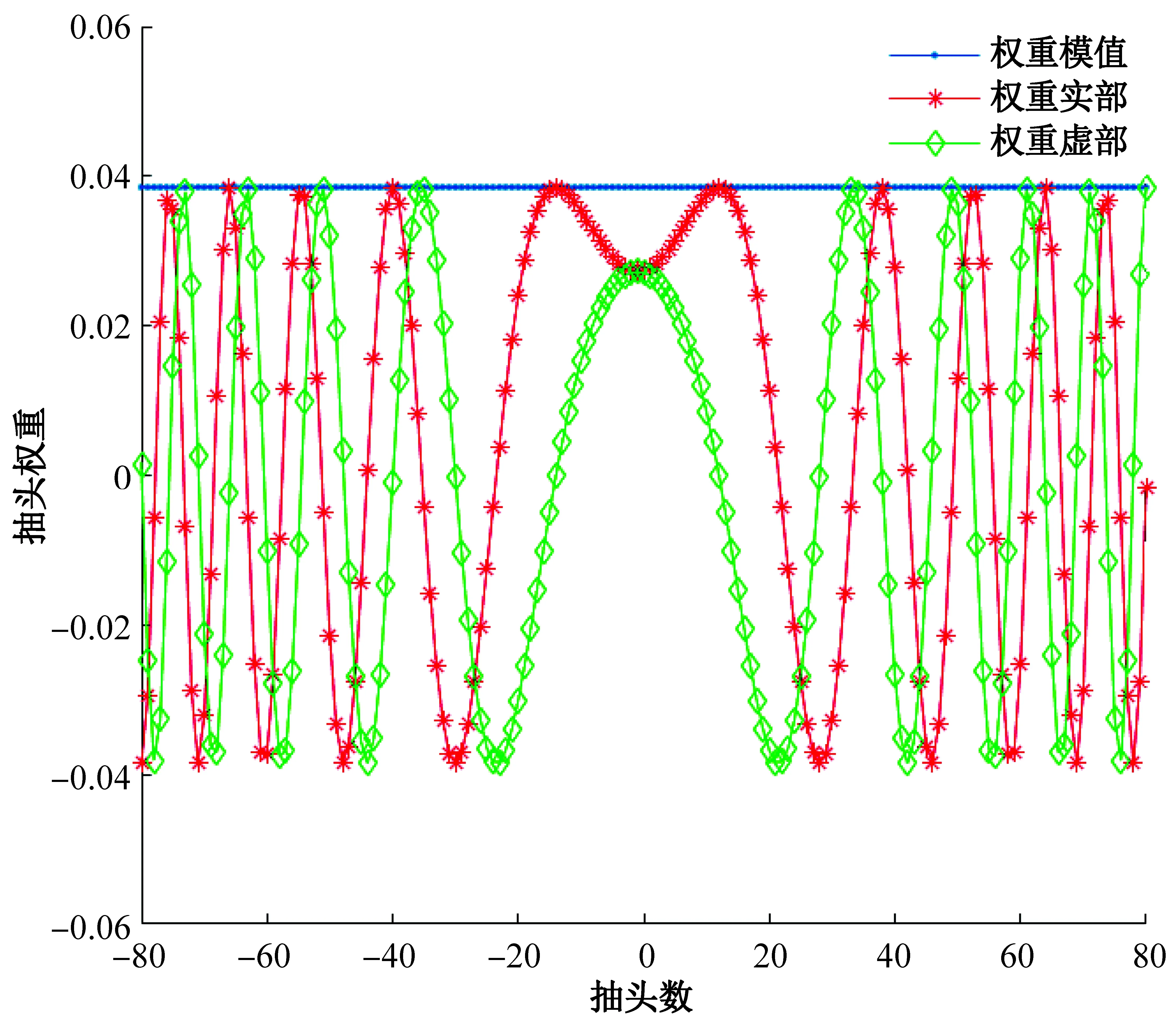
图2 TDE抽头权值Fig. 2 TDE tap weights

DSP处理模块中的均衡算法通过对接收信号x(n)抽样后的数据点进行“迫零”处理，从而消除ISI影响，下面推导其原理。

设发射信号s(n),经过长度为L的离散信道传输后的接收信号可表示为

(5)

式中：hl为FIR离散信道单位冲激响应；v(n)为加性高斯白噪声(additive white gaussian noise,AWGN)。考虑到抽头数为2M+1的均衡滤波器单位冲激响应为

(6)

(7)

将式(5)代入式(7)得

(8)

经过变量代换l=k+i，得

(9)

式中f(n)为h(n)与w(n)线性卷积和；式中第一项与发射信号成比例，第二项为码间串扰值，第三项为噪声影响。为消除ISI，f(n)应满足

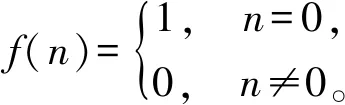
(10)

基于静态色散补偿的MDD-LMS算法流程如图3所示。

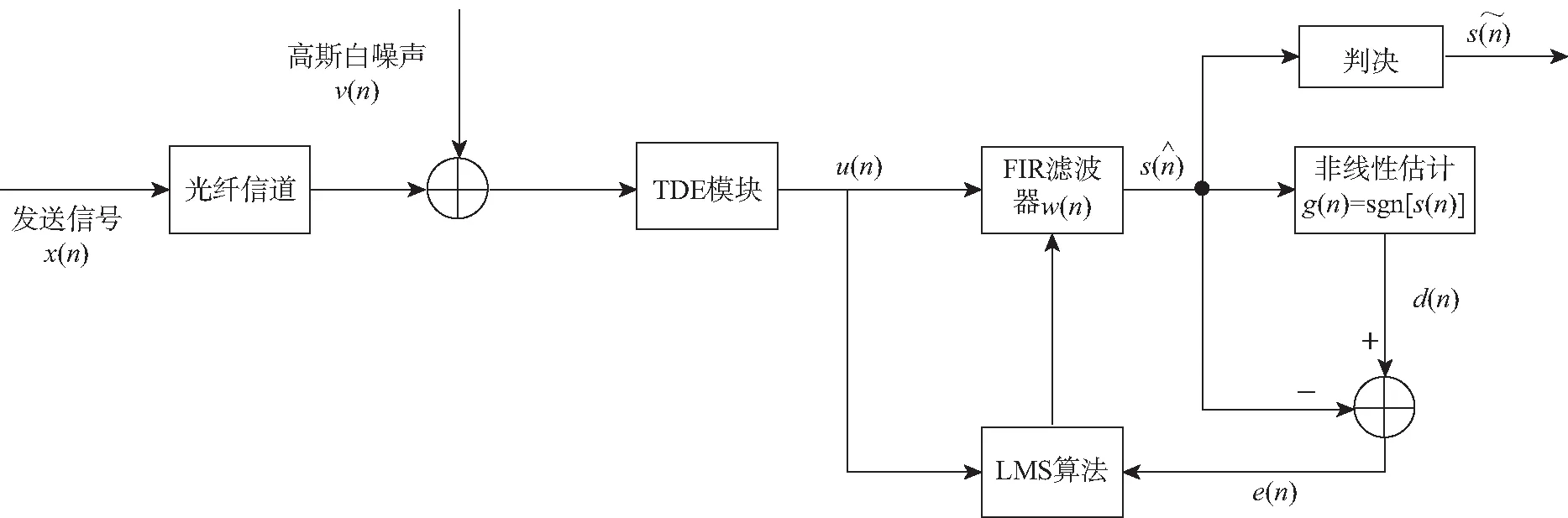
图3 MDD-LMS算法原理Fig. 3 Schematic diagram of MDD-LMS algorithm

利用信道盲均衡原理，构建代价函数

(11)

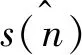
JM(n)=J[w(n)]+αJ[w(n-1)]。

(12)

式(12)可化为

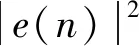
(13)

根据经典维纳滤波器理论，可求得横向滤波器迭代公式为

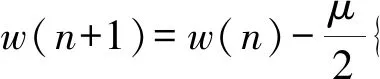
(14)

w(n+1)=w(n)+μu(n)e*(n)+α[w(n)-w(n-1)]。

(15)

考虑到MDD-LMS算法性能以及动量因子α的选取，设ξwi=w(n+1)-w(n)，式(15)可表示为ξwi(n)=μe(n)u(n)+αξwi(n-1)，设γ(n)=e(n)u(n)，可得

(16)

式中引入α的幂次累加项，MDD-LMS算法初期收敛速度加快，追踪能力加强；迭代近稳态时，动量的引入可以帮助稳定误差曲线。由于存在非线性项，前向累加误差难免会对收敛稳态值产生一定波动。

本文在MATLAB中搭建224 Gbps NRZ-QPSK光纤传输信道，设置色散常数为16 ps/(nm·km-1)，传输距离为100 km，在OSNR为10 dB的情况下，比较传统定步长DD-LMS算法与MDD-LMS算法的误差曲线，如图4和图5所示。

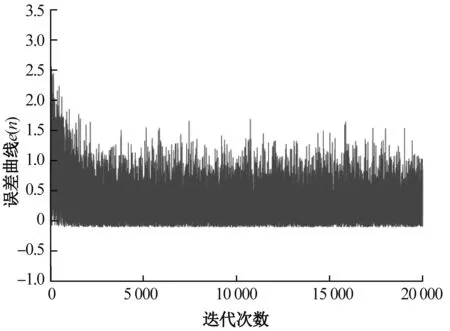
图4 MDD-LMS误差曲线Fig. 4 MDD-LMS error curves

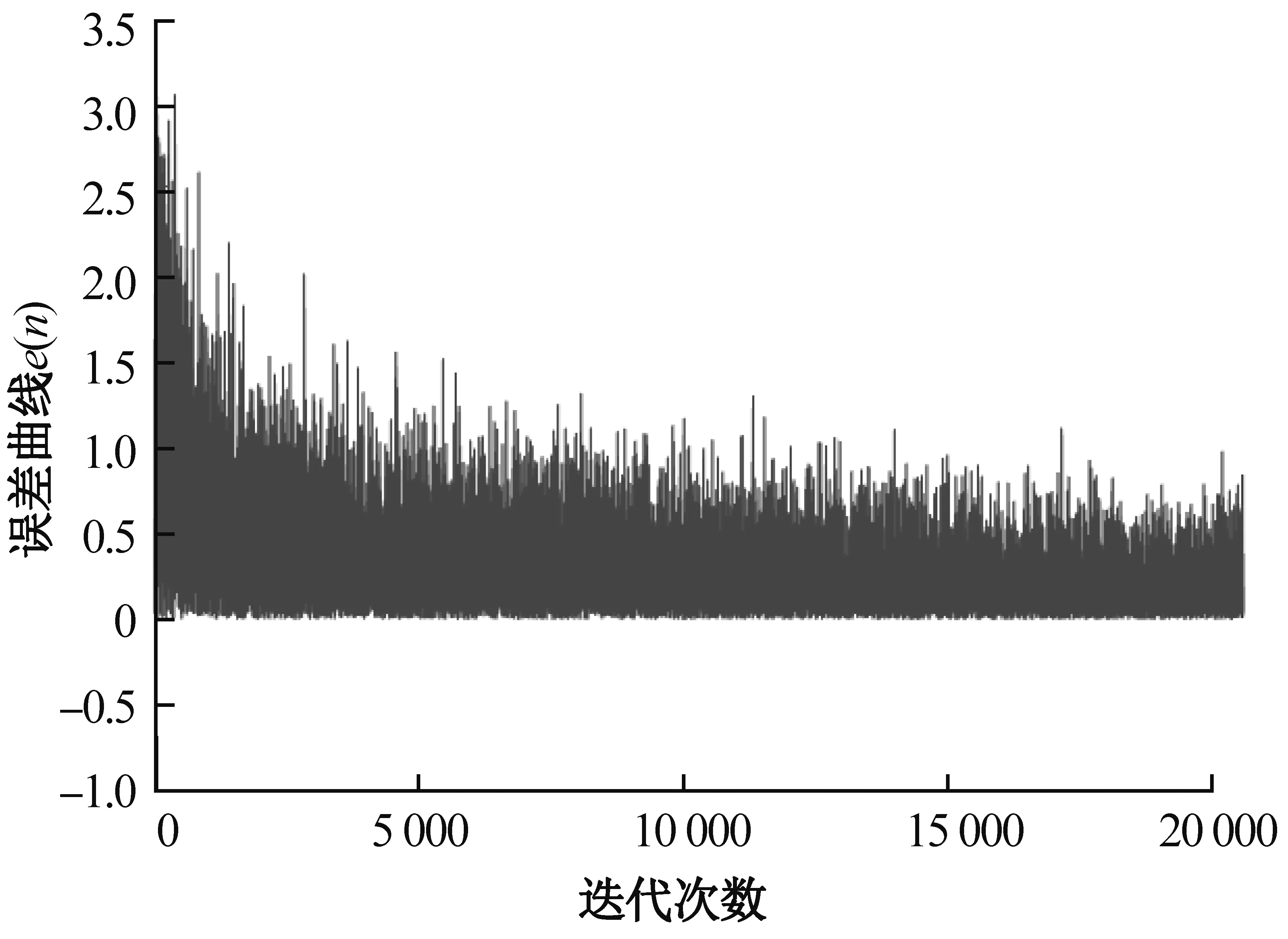
图5 DD-LMS误差曲线Fig. 5 DD-LMS error curves

可以看出，MDD-LMS算法收敛性优于DD-LMS算法，然而稳态误差稍大一些。综合来说，引入动量项的DD-LMS算法性能优于传统的DD-LMS算法。

增加动量项后，当n→∞时，设理想抽头权重为w0，定义权向量误差为

ε(n)=wi(n)-w0。

(17)

由MDD-LMS算法迭代公式

(18)

考虑到高次动量项对收敛性能影响不大，保留一次动量项后可得

E{ε(n+1)}=E{ε(n)}-(μ+α)RE{ε(n)}。

(19)

即E{ε(n+1)}=[I-(μ+α)R]E{ε(n)}，其中I为单位矩阵，R为输入向量u(n)的自相关矩阵。可得步长μ和α的关系为

(20)

式中λmax为R的最大特征值。

考虑到动量因子α决定MDD-LMS算法收敛速度和稳态误差，迭代初期收敛速度是首要因素，待算法趋近稳定后，使用动量因子帮助稳定误差。因此不同类型的动量因子对算法的优化性能不尽相同，本文探究指数动量因子(exponential momentum factor)、线性动量因子(line momentum factor)、乘幂动量因子(power momentum factor)和有理函数动量因子(rational momentum factor)对DD-LMS算法收敛性的提升。不同类型的动量因子模型如图6所示。

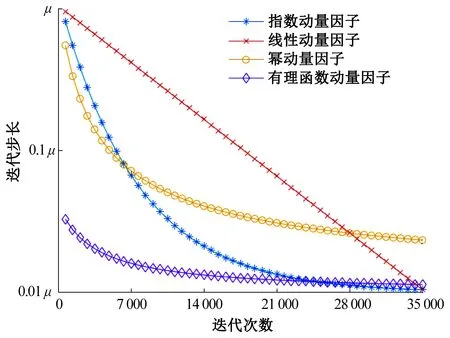
图6 不同函数模型的动量因子Fig. 6 Momentum factors of different functional models

本文通过中心抽头的收敛性，比较了MDD-LMS算法、传统DD-LMS算法以及变步长DD-LMS算法(variable step-decision-directed least mean-square，VS-DD-LMS)。设置横向滤波器抽头数为13，迭代步长μ为0.000 1，α区间为[2×10-7，2×10-5],仿真结果如图7所示。由图7可以看出，指数因子MDD-LMS算法迭代次数在4 000左右即可达到稳态，而其他类型动量因子的DD-LMS需迭代近30 000次才趋近收敛。引入动量项对盲均衡算法收敛性的改善显而易见。在高速光接收机中，盲均衡算法需在迭代前期快速收敛，动量项的引入提升了盲均衡算法的追踪能力，动量因子α取值越大，收敛速度和追踪性能提升越大，但这种优化并非没有代价，算法趋近稳态后，系统中会引入一定量的残余误差，此时可以通过迭代步长μ和动量加权因子α来改善稳态性能，因此盲均衡算法迭代初期采用较大的α用于提升算法跟踪速度；待系统达到稳态后，通过动量因子α的衰减来控制稳态误差。由图5和图6可得，对比不同类型的动量因子，无论是在收敛速度还是在稳态误差控制方面，指数动量因子衰减模型相较于其他类型动量因子模型更加契合盲均衡算法。

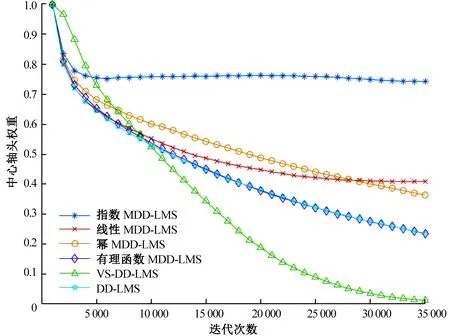
图7 动量因子对自适应均衡器中心抽头收敛性影响Fig. 7 Influence of momentum factor on center tap convergence of adaptive equalizer

2 实验结果

2.1 误码率分析

本文数字相干光接收机采用单载波224 Gib/s的传输方案。仿真实验基于Matlab和OptiSystem光学仿真软件，考虑到实际相干光系统，采用标准单模光纤(single mode fiber,SMF)，使其工作波长位于1 550 nm处，SMF中一般色度色散常数为16 ps/(nm·km-1)，考虑到传输距离增大时，二阶色散对传输信号影响加剧，设置二阶色散常数为0.075 ps/(nm2·km-1)。由光纤Kerr效应引起的非线性损伤[14-18]，在传输光功率较小时忽略不计，其他仿真参数如表1所示。

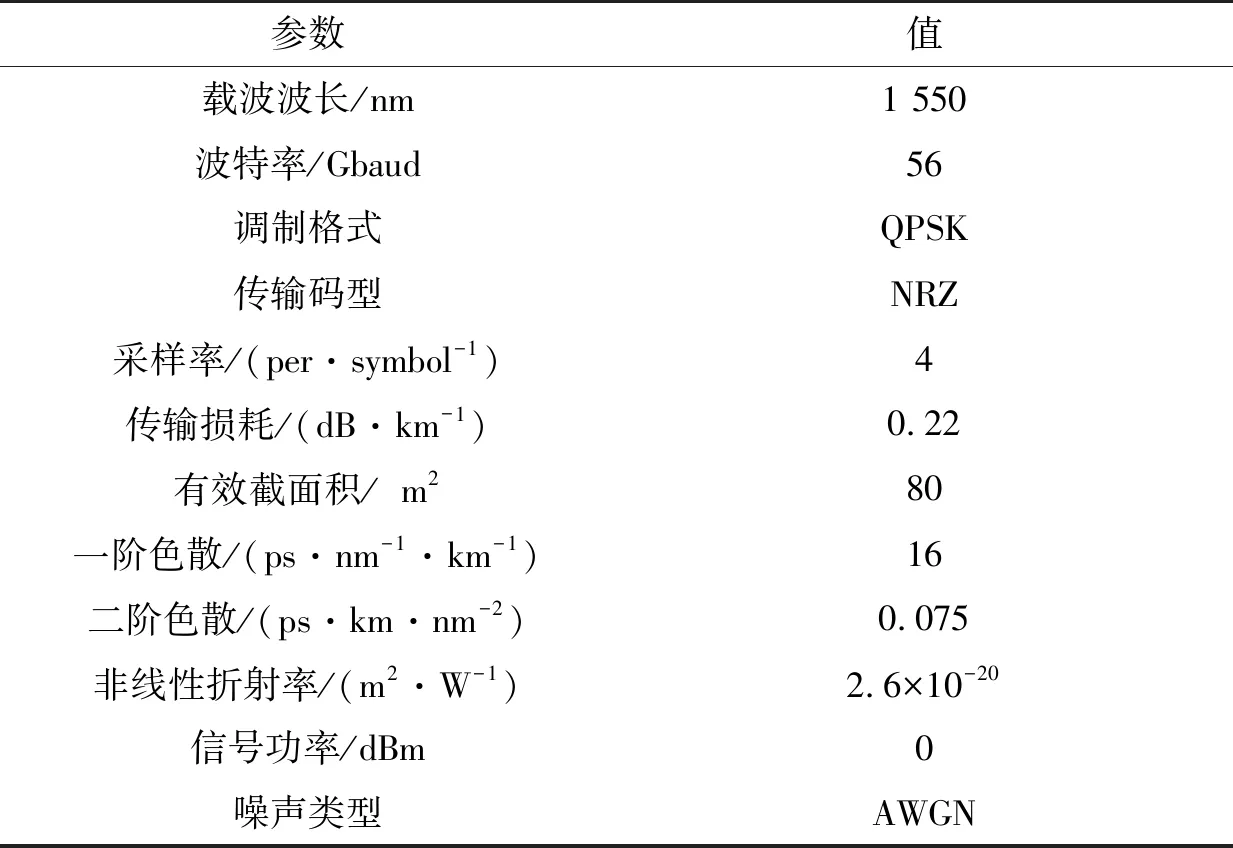
表1 相干传输系统仿真参数

在未添加前向纠错码[19-22](forward error correction,FEC)的情况下,设置光纤长度为500 km，MDD-LMS算法迭代步长为0.000 1，动量因子为指数模型，忽略偏振模色散(polarization mode dispersion,PMD)的影响，测试所得光信噪比与误码率如图8所示。

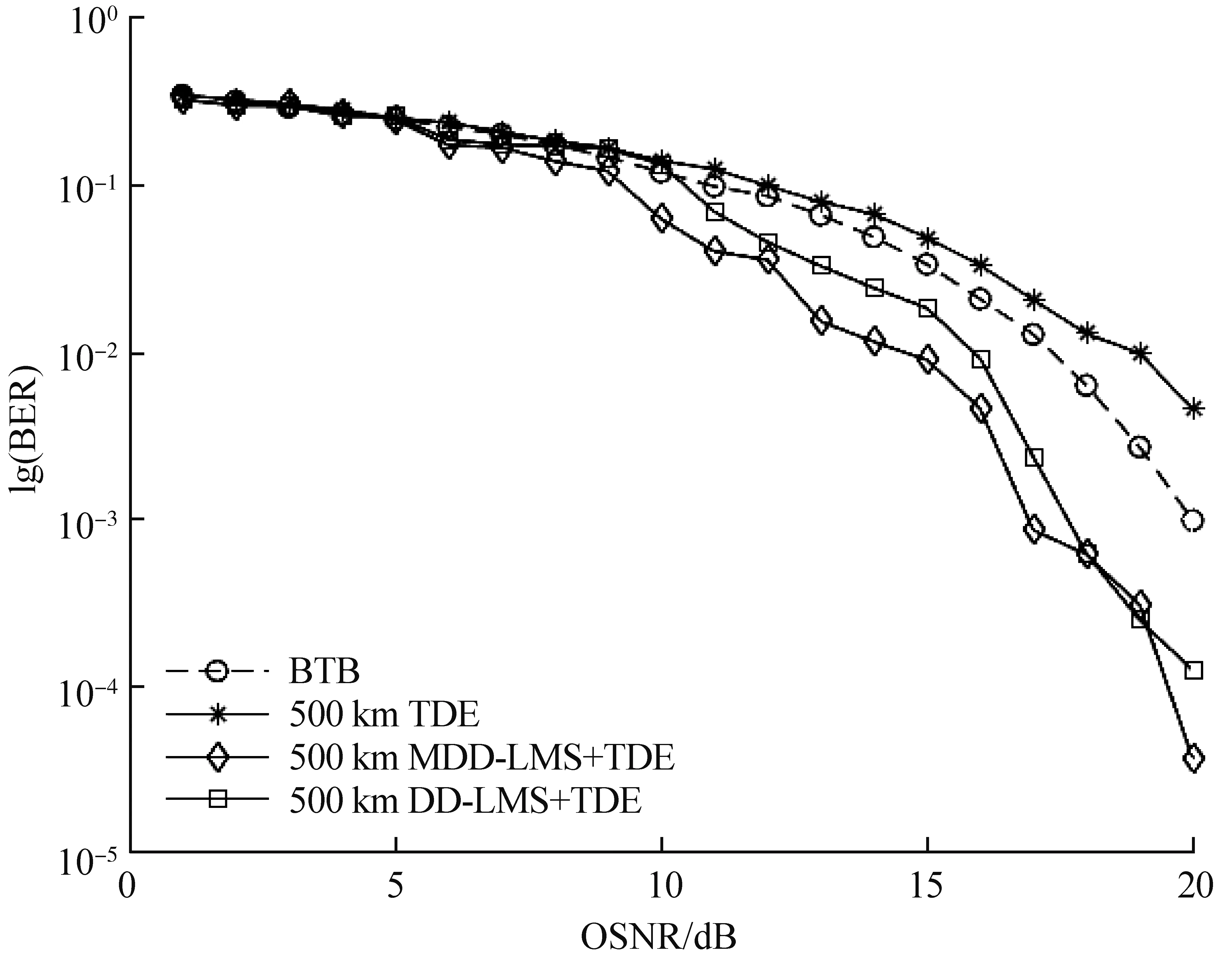
图8 光信噪比与BER的关系Fig. 8 Relation diagram of OSNR ratio and BER

图8分别对比了时域色散补偿FIR滤波器性能和添加DD-LMS或MDD-LMS自适应滤波器后色散均衡器的性能，同时对比参考了背靠背(back-to-back,BTB)情况下系统的误码率。可以看出，在低OSNR情况下，各类算法差距不大，而TDE模块由于其本身FIR滤波器特性限制，无法完全均衡静态色散影响，在OSNR为10 dB之后性能逐渐下降，20 dB情况下误码率达到4.57×10-3。在TDE后端增加MDD-LMS算法模块后，随着OSNR增大，系统的误码率下降较为明显，在20 dB时，BER降低到3.707×10-5，相比传统TDE模块，系统误码率下降了约2 dB。结果证明添加MDD-LMS算法后的均衡方案对光纤信道中的静态色散损伤具有较好的补偿作用。图8同时对比了DD-LMS算法和MDD-LMS算法的BER性能。由于本身的盲均衡特性，MDD-LMS的BER浮动在-0.354 8 dB左右,与DD-LMS算法类似，2种算法的BER曲线图存在一定的波动，但总体差异不大。从实际工程角度而言，指数因子MDD-LMS算法由于在收敛速度和追踪性能上的优势，更适用于实际高速光传输系统。

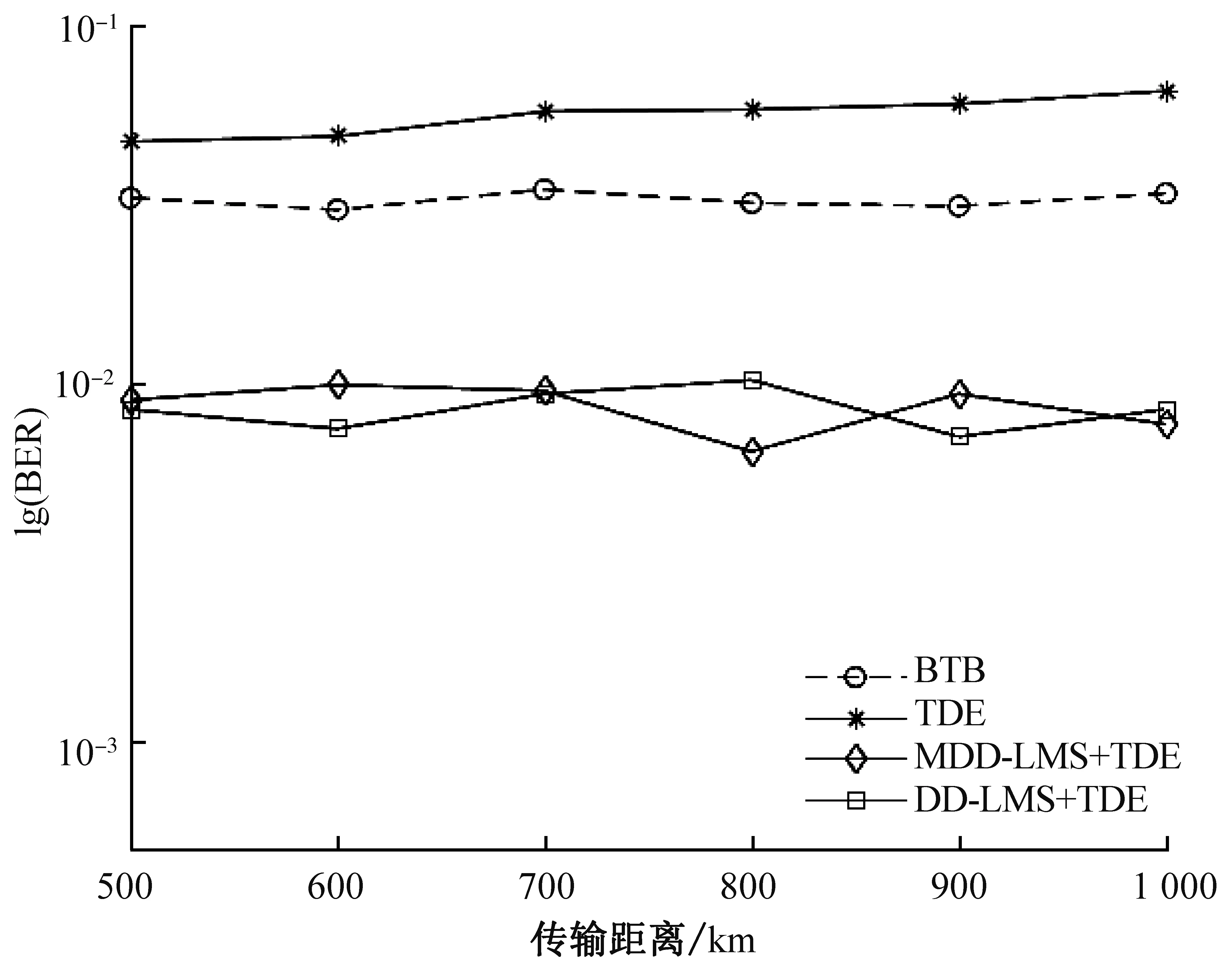
图9 光信噪比为15 dB情况下光纤长度与误码率的关系Fig. 9 Relation diagram of fiber length and bit error rate at optical signal-to-noise ratio of 15 dB

考虑到单模光纤中色散参数D与光纤长度有关，本文同时测试了传输距离对MDD-LMS算法的影响，结果如图9所示。图9对比了在光信噪比为15 dB的情况下，添加MDD-LMS算法模块对TDE的影响。TDE模块随着传输距离逐渐增大，误码率有一定的上升趋势。而MDD-LMS由于其本身具有较强的抗干扰能力，总体误码率处在一定范围之内，在色散信道中具有较好的鲁棒性。在传输距离为1 000 km时，其误码率可达到10-2。

2.2 计算复杂度比较

本文从各类算法的均衡过程来分析TDE、DD-LMS、MDD-LMS算法实现的计算复杂度，设输入信号长度为M，自适应横向滤波器长度为L，分析结果如表2所示。

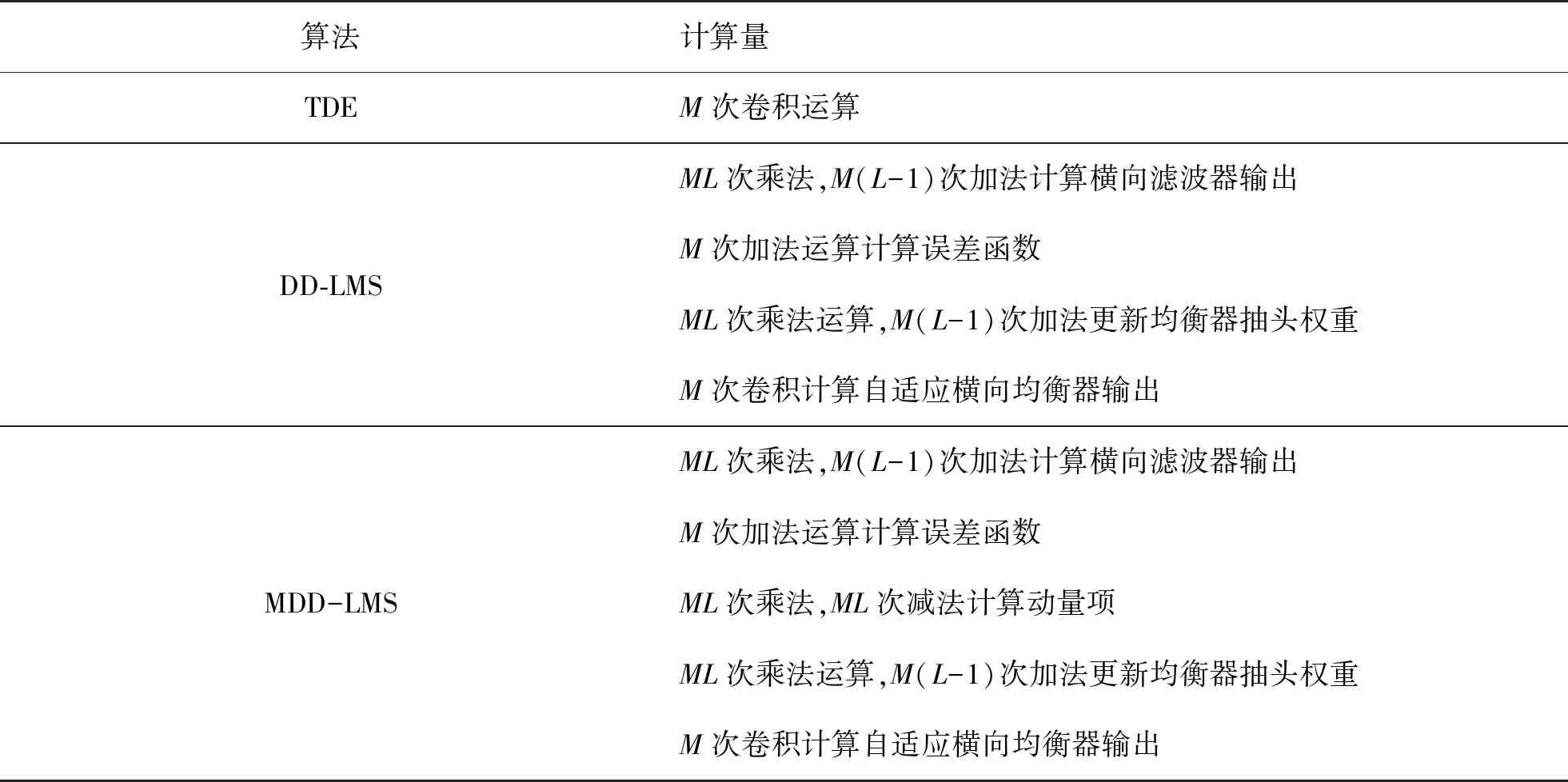
表2 各类均衡算法计算复杂度

本文所搭建的单载波56 Gbaud PM-QPSK系统中，在传输距离为1 000 km的情况下，由式(4)计算出TDE所需抽头数为N=1 683个，其均衡静态色散所需计算量为N与信号长度M的卷积运算。后续添加的DD-LMS算法所设置的抽头数为L=13，根据经典盲均衡算法迭代过程，单次迭代所需计算量仅为2L次乘法运算和2L-1次加法运算。MDD-LMS算法引入动量因子后在原有DD-LMS算法的基础上仅增加了2L次加法运算和L次乘法运算，增加后的计算总量约为TDE的1.5%。在几乎没有提升接收机计算复杂度的条件下，MDD-LMS算法有效地抑制了残余色散的影响，证明本算法在实际系统中的可行性。

3 结语

本文采用动量因子改进了盲信号处理理论中的判决引导算法，通过仿真实现了MDD-LMS算法模块在单载波传输速率为224 Gib/s的高速光接收机色度色散补偿中的应用。指数因子MDD-LMS算法与传统DD-LMS算法在色散均衡方面性能相近，能有效地降低光纤中色度色散的影响;但指数因子MDD-LMS算法的收敛速度仅约为DD-LMS算法的1/10，其跟踪能力方面远优于VS-DD-LMS和其他类型MDD-LMS算法，更适合高速光接收机。由于实际光纤通信系统信道的复杂度和当前电子器件工作频率限制，后续改进算法还需针对系统的稳定性加以研究。