步履式顶推曲线钢箱梁桥倾覆稳定性研究

2022-03-25吴大俊唐益军李雪红

现代交通技术 2022年1期

余满，吴大俊，唐益军，李雪红

(1. 江苏宁沪高速公路股份有限公司，南京 210049； 2. 南京工业大学土木工程学院，南京 211816)

与传统顶推法的拖拉方式不同，步履式顶推施工是通过一套液压千斤顶设备来进行梁体的连续式顶推。其优势在于由液压电器控制并集顶升、平移和横向调整于一体，精度和同步性能得到较好控制；能够控制墩顶所受水平力；竖向调整较方便；当箱梁局部应力超过限度时，可通过调整竖向千斤顶的伸缩量控制各个支点反力。桥梁步履式顶推施工工艺也因其高效可靠且对桥下设施影响较小等优点在桥梁施工中逐步应用，但由于该工艺尚处于应用初期阶段，在施工中的倾覆稳定性研究尚不充分。对于曲线形钢箱梁桥，由于其自重轻、曲率大等结构特点，在采用步履式顶推施工时，其倾覆稳定性问题尤为突出，有必要开展工程分析及控制技术研究，避免相关事故发生。步履式顶推系统工作原理如图1所示。

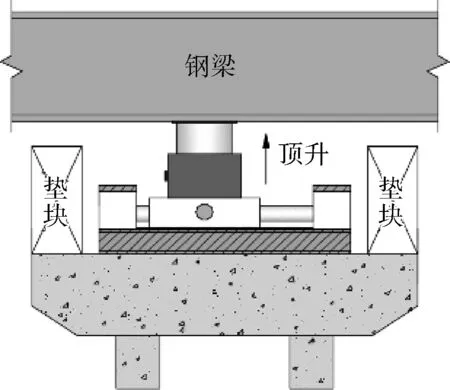
(a) 顶升

黄志华[1]通过对某钢箱梁顶推施工工艺的总结，得出步履式顶推法具有安全灵活、高效便捷并且控制要求高等特点。谢福君等[2]结合某钢箱自锚式悬索桥，分析导梁各设计参数对顶推受力及变形的影响，结果表明导梁的长度及其平均线重度对顶推受力及变形的影响较大。李怀雷[3]以实际工程为基础，分析影响弯桥顶推施工中梁体内外侧位移不同以及梁中线偏移等问题的影响因素，并提出千斤顶纠偏的具体解决措施。已有研究主要着眼于顶推施工工艺分析，而对步履式顶推施工过程中倾覆稳定性问题研究尚不充分。

针对曲线钢箱梁桥的步履式顶推施工过程，研究结构主要参数及主要影响因素对倾覆稳定性的影响规律，归纳相关控制方法，并提出量化控制标准用于指导工程的施工控制。

1 研究对象和内容

已有研究表明[4]，影响桥梁倾覆稳定性的主要因素包含支点脱空、支点纵横向间距以及轴线偏移等。曲线钢箱梁桥布置示意如图2所示，以4×40 m 跨径曲线钢箱梁桥为研究对象，该桥采用单箱双室闭合截面，桥梁顶板宽为13 m，底板宽为9.2 m，悬臂长为1.9 m，曲率半径为400 m。针对各影响因素进行系统分析，其中结合支点所在截面分别考虑1-1、2-2、3-3和4-4截面内外侧支座分别脱空；支点横向间距的确定与桥宽相关联，主要考虑B/2、7B/12、2B/3、5B/6、B(B为桥宽)情况下的5种工况；支点纵向间距的选取与跨径相结合，主要考虑L/6、L/3、L/2、2L/3(L为跨径)情况下的4种工况；轴线偏移结合施工过程中的控制标准，主要考虑0 cm、5 cm和10 cm的3种偏移量。此外为使分析结果具有普适性，还应考虑不同桥梁设计参数，曲率半径具体参考《公路工程技术标准》(JTG B01—2014)[5]，分别考虑100 m、150 m、200 m、400 m和600 m 的5种尺寸，顶推长度结合工程实际情况及施工设备，主要考虑40 m、80 m和120 m情况下的3种工况，桥宽主要考虑单车道、双车道和三车道情况下的3种工况，即桥宽分别为8.4 m、13 m和17.6 m。

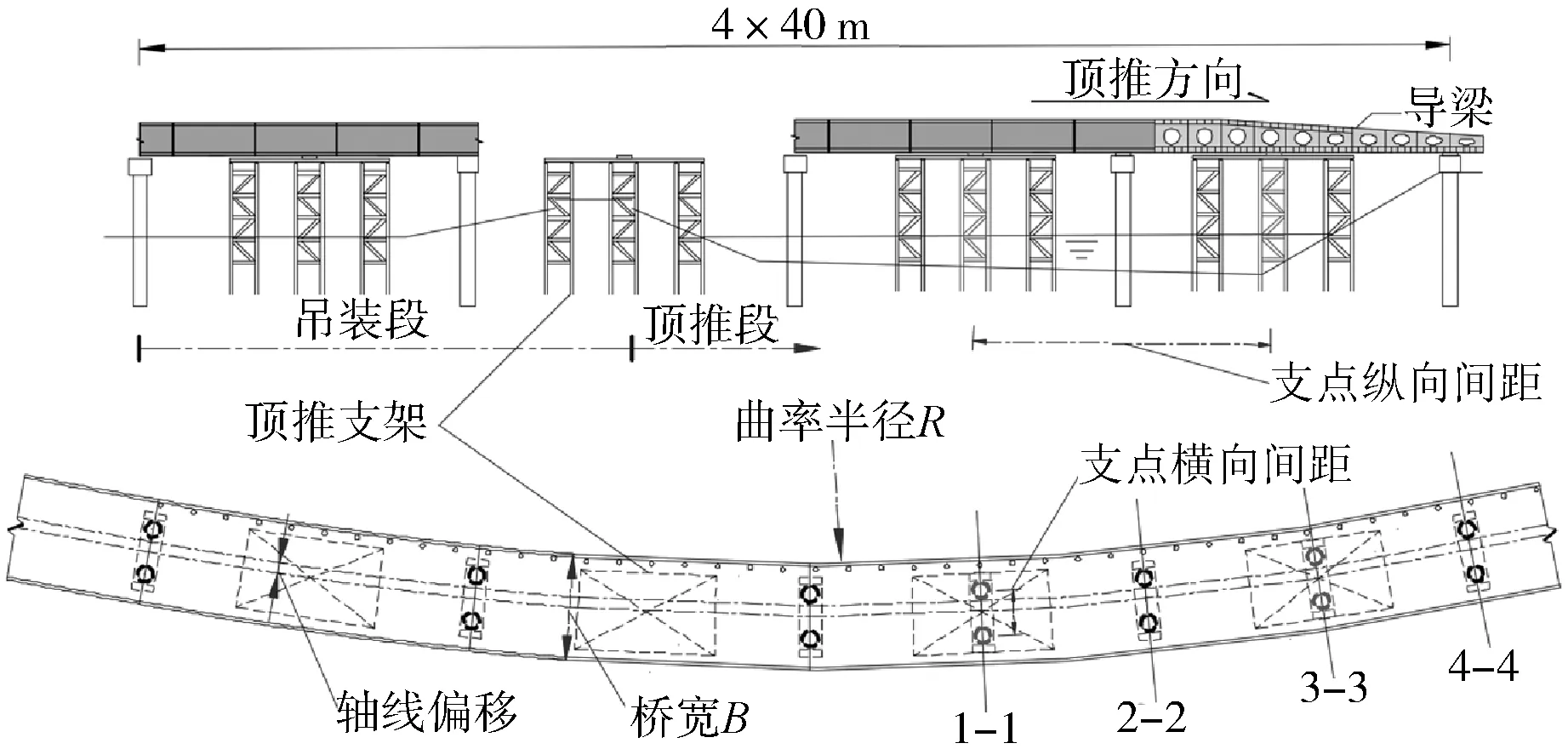
图2 曲线钢箱梁桥布置示意

2 稳定性计算方法及有限元模型

2.1 倾覆稳定性计算方法

桥梁倾覆过程复杂，一般认为支座失效或脱空是倾覆的开始。曲线梁桥在弯-扭耦合效应下，外侧支座反力变大，内侧反力变小甚至出现负反力。根据梁体在静止情况下力和力矩的平衡状态，荷载产生的作用力大小等于所有支座反力之和，荷载产生的扭矩在数值上等于支座反力产生的扭矩。因此荷载的作用力相对于偏离梁体中心线距离为e的位置产生一个大小为F的总荷载，截面示意如图3所示，可得计算公式：

(1)

式中，e为荷载的偏心距；F内、F外分别为内侧和外侧支座的支座反力；e内、e外分别为内侧和外侧支座与梁体中心线的距离。

横向倾覆稳定系数(以下简称稳定系数)可定义为[6]：k=e外/e，其中k的容许值取2.5[7]。当k=e外/e且k>2.5时，表明横向倾覆稳定性满足要求。

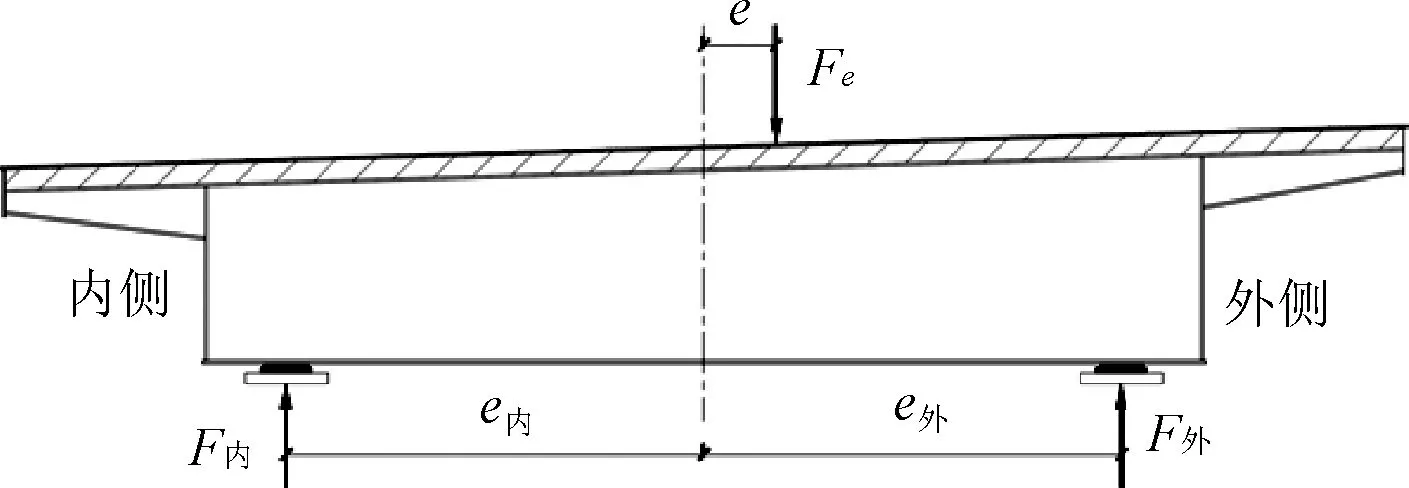
图3 截面示意

2.2 有限元模型

借助有限元分析软件MIDAS Civil建立钢箱梁模型，分析顶推过程中各阶段钢箱梁的支点受力状态。其中钢箱梁和导梁均用梁单元模拟，钢箱梁与导梁之间采用刚性连接。模型边界条件定义为：当钢箱梁和导梁架在临时墩上时，加竖向约束，临时墩墩顶与梁之间采用弹性连接。有限元模型如图4所示。

图4 有限元模型

3 主要设计参数对倾覆稳定性的影响分析

参照倾覆稳定性计算方法，结合MIDAS软件计算所得的支座反力，可得到各工况下的倾覆稳定系数k。根据稳定系数相应变化情况，可分析不同设计参数对钢箱梁桥在顶推施工过程中的稳定性影响，具体分析如下。

3.1 曲率半径对稳定性的影响

为分析曲率半径的影响，桥宽和顶推箱梁长度保持不变，分别为13 m和80 m。在不同支点脱空位置、支点间距和轴线偏移量情况下，不同曲率半径对稳定系数的影响变化曲线如图5所示。稳定系数随曲率半径的变化曲线表现出相似的变化规律，当曲率半径<150 m时，稳定系数随曲率半径的增大而减小，稳定性逐渐降低；当曲率半径>150 m后，稳定系数随着曲率半径的增大而增大，稳定性逐渐增强，在150 m左右时稳定性相对较差。经分析这主要与倾覆轴线的变化有关，当曲率半径<150 m时，倾覆轴线落在支座连线外，但其与加载车道围成的面积变小，即上部结构产生倾覆的作用变小；当曲率半径>200 m时，倾覆轴线落在支座连线内，倾覆力矩减小。因此设计时，在满足工程线形要求的前提下，应尽量避免选用150 m左右的曲率半径。

(a) 不同支点脱空位置

3.2 顶推跨径对稳定性的影响

为分析顶推跨径的影响，桥宽和曲率半径保持不变，分别为13 m和400 m。在不同支点脱空位置、不同支点间距和轴线偏移量情况下，不同顶推跨径对稳定系数的影响变化曲线如图6所示。稳定系数随顶推跨径的增大而减小，当顶推跨径由40 m 增大到80 m时，稳定系数明显降低，降低幅度达40%～70%；由80 m增大到120 m时，稳定系数的变化幅度有所降低，为5%～20%。因此在顶推过程中应尽量减小顶推跨径，宜控制在60 m以内，以保障施工过程中的横向稳定性。

(a) 不同支点脱空位置

3.3 桥宽对稳定性的影响

在分析桥宽变化的影响时，曲率半径和顶推长度分别取400 m和80 m，对单车道、双车道和三车道3种较常见的车道进行研究，对应的桥宽分别为8.4 m、13.0 m和17.6 m。在不同支点脱空位置、支点间距和轴线偏移量情况下，不同桥宽对稳定系数的影响变化曲线如图7所示。桥宽与稳定系数之间的关系表现出一定的不确定性，当支点脱空位置和支点间距发生变化时，稳定系数随桥宽的增大呈现出增大趋势，增大幅度有所不同，在5%～50%之间变化，桥宽较窄时稳定性更为不利；而轴线偏移时，稳定系数则随着桥宽的增大而减小，对宽桥更为不利。因此对于窄桥，控制支点脱空和支点间距的影响更为重要；对于宽桥，更应关注对轴线偏移的控制。

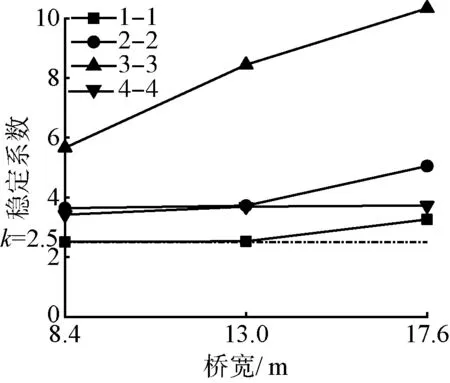
(a) 不同支点脱空位置

4 顶推施工参数对倾覆稳定性的影响及其控制

4.1 支座脱空的影响分析

内弧侧支点脱空时稳定系数的变化曲线如图8所示，外弧侧支点脱空时稳定系数的变化曲线如图9 所示。综合桥梁参数和内外侧支点脱空变化规律可以发现：①结构的边支点(1-1、4-4)脱空后的稳定系数明显小于中间支点脱空后的系数，并且会出现小于2.5的情况，有可能发生横向倾覆失稳，因此在施工中应注意避免边支点脱空；②外弧侧支点脱空时的稳定系数总体小于内弧侧支点脱空时的稳定系数，比内弧侧支点脱空更为不利，应重点关注。总之在步履式顶推过程中，应严格控制各支点顶推力，使其均衡受力、共同作用，避免支点脱空，尤其要避免边支点和外弧侧支点的脱空。

(a) 不同曲率半径

4.2 支点间距的影响分析

稳定系数随支点横向间距的变化曲线如图10所示，稳定系数随支点纵向间距的变化曲线如图11所示。分析可知：①不同的曲率半径、顶推跨径和桥宽，稳定系数均表现出相似的变化规律；②随支点间距的增大，稳定系数明显增大，支点间距较小时可能发生倾覆失稳，当横向间距<7B/12(B为桥宽)或纵向间距

(a) 不同曲率半径

4.3 轴线偏移的影响分析

稳定系数随轴线偏移量的变化曲线如图12所示。分析可知：不同的曲率半径、顶推跨径和桥宽，稳定系数随轴线偏移量的变化规律相似，均随轴线偏移量的增大而减小。当轴线偏移量<10 cm 时，稳定系数基本>4，具有一定安全储备。因此在施工过程中，应控制轴线偏移量不宜过大，建议不超过10 cm，并及时纠偏，以确保施工安全。

(a) 不同曲率半径

5 施工过程稳定性控制

针对曲线钢箱梁桥的步履式顶推施工，除参考上述关键的设计和施工参数外，结合施工监测技术，在施工过程中还应采取相应控制措施，以确保曲线钢箱梁桥在顶推过程中能够实现有效落梁。

(1) 考虑到顶推过程中支点受力不均匀的影响，在设计中应考虑增加临时墩及梁体的安全储备系数，同等条件下选择曲率半径较大的设计方案，可增大桥梁在施工中的抗倾覆稳定性。

(2) 在施工过程中，支点脱空可能产生虚接触，以滑块是否滑动作为判断依据，在梁体处于滑动、滑块不动的情况下，表明已经脱空。

(3) 施工过程中应严格控制千斤顶的转向，保证各个千斤顶的同步性。

(4) 结构稳定性受支点纵横向间距的影响很大(尤其是结构的倾覆稳定性)。通过研究，结合实际工程中的有效运用，可以得出施工中的支点横向间距在7/12B～B时，能够保证结构的倾覆稳定性满足规范要求。如果现场无法达到条件，可允许中支点横向间距不在此范围内，但边支点的间距应尽量大；支点纵向间距在一定范围内应保证其超过L/3。同时现场施工环境较恶劣时，应设置抗倾覆装置，保证施工中结构的抗倾覆稳定性。