虚拟轨道列车多轴协同预瞄循迹控制方法

崔 涛，王 淇，刘学刚，贾星衡，王 硕，王文军

(1.中车唐山机车车辆有限公司，河北 唐山 063000；2.清华大学 车辆与运载学院，北京 100084；3.吉林大学 机械与航空航天工程学院，长春 130022)

近年来，对于清洁、便捷、高效的运输方式的研究受到人们广泛关注. 相比较传统汽车，多铰接式虚拟轨道列车运输量大，可增加单程运输效率. 采用多铰接式虚拟轨道列车相比传统汽车可降低约30%能源消耗，还可以降低40%的道路磨损[1-2]，大幅提升能源利用效率. 相比较现有的轻轨列车，多铰接虚拟轨道列车不需要铺设轨道，可充分使用现有道路条件，大大降低了建设成本.

多轴转向的多铰接虚拟轨道列车转向控制难度较大. 例如，具有多轴转向的多铰接虚拟轨道列车[3-5]设计为具有差动转向功能的驱动转向一体化模块架构，转向自由度多，增加了转向控制的难度.孙帮成等[4-5]采用非时间因素的控制策略，并结合李雅普诺夫函数证明该控制策略下虚拟轨道列车能够沿目标直线路径行驶. Yamaguchi等[6]针对三轴主动转向的五轴车辆也基于李雅普诺夫函数设计了一种路径跟踪方法. 针对多铰接车辆模型的复杂性，有的研究工作对模型进行了线性简化. 例如，Bolzern等[7]采用输入-输出线性化方法对多铰接虚拟轨道列车进行循迹控制，搭建牵引车转向模型，介绍了设置目标轨迹上跟踪点的方法，以及计算车辆与跟踪点距离偏差的方法，以使列车可以双向行驶. 并且通过仿真验证了该方法下列车在曲线上横向偏差的动态收敛性. Kim等[8]基于线性二次调节器提出了对多铰接车的主动控制策略，包括对牵引车和挂车的控制. 还有的研究工作在单节车阿克曼转向模型的基础上构建多铰接车的循迹策略。例如，Wagner等[9]研究了全挂和半挂混合的双铰接式客车，提出了基于运动学车辆模型设计的类似轨道列车的循迹控制方法和基于运动学模型设计的扩展阿克曼转向模型两种自动转向控制方法，用以提高双铰接客车的循迹能力.张立伟等[10]在阿克曼转向模型的基础上，采用航向角预估控制算法，依靠增量PID算法补偿模型误差，从而实现车辆路径跟随控制. 在控制方面，有学者利用模糊控制解决多铰接车辆的循迹控制问题. Tanaka等[11]提出了一种基于模型的模糊控制方法，并利用Lyapunov稳定性理论进行了稳定性分析，可以实现对铰接车辆的倒车运动进行控制. 文献[12]针对双挂车行驶问题也提出了一种基于模糊控制的倒车稳定性控制方法，其控制器参数可以通过线性矩阵不等式求解得到. 在实验方面，Sampei等[13]针对曲线行驶工况，基于车辆运动学模型给出了一种非线性转角指令的控制方法，并且进行了“8字绕环”实验验证. Tanaka等[14]又提出了一种应用于三节挂车的循迹控制方法，给出了渐进稳定条件，并且进行了模型实验进行验证. 在以上的研究工作中，文献[5]中提出的多铰接虚拟轨道列车的控制方法不能直接应用于车辆航向角变化量为90°的行驶工况. 文献[7]中只提出了针对多铰接车辆牵引车的控制，没有明确说明对于拖车部分的控制策略. 文献[8]中研究了单节虚拟轨道列车的稳定性问题，但没有对列车在行驶过程中的轨迹内移问题做相关研究.

综合现阶段对多铰接虚拟轨道列车的循迹控制研究难点，本文作者在文献[3]所提出的多铰接虚拟轨道列车架构以及自动驾驶车辆特点的基础上，采用多刚体动力学软件搭建了多铰接虚拟轨道列车仿真模型，并提出了一种基于单点预瞄的多铰接虚拟轨道列车协同转向控制策略. 最后通过仿真分析验证了提出的控制策略可以使多铰接虚拟轨道列车在直线和曲线工况下实现较好的轨迹跟随，为后续对多铰接虚拟轨道列车行驶稳定性的研究奠定了基础.

1 多铰接虚拟轨道列车仿真模型

多铰接虚拟轨道列车由4个驱动转向模块和3节车厢组成，车厢之间通过驱动转向模块进行连接，通过各驱动转向模块左右的驱动电机差动转向来控制虚拟轨道列车的行驶轨迹. 在多刚体动力学分析软件Simpack中搭建其仿真模型，如图1所示，其中长度较短的模块为驱动转向模块，各驱动转向模块之间的较长的框体为车厢部分.

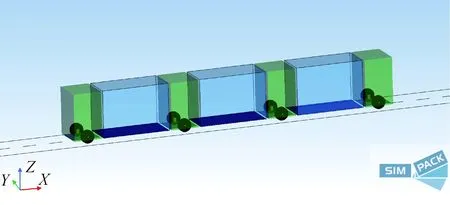
图1 多铰接虚拟轨道列车Simpack仿真模型Fig.1 Simulation model of the multi-axle virtual railway vehicle in Simpack

Simpack模型的拓扑结构如图2所示，整列多铰接车共有3节车厢，4个驱动转向模块. 连接虚线表示铰接的自由度，连接实线表示被约束的自由度.

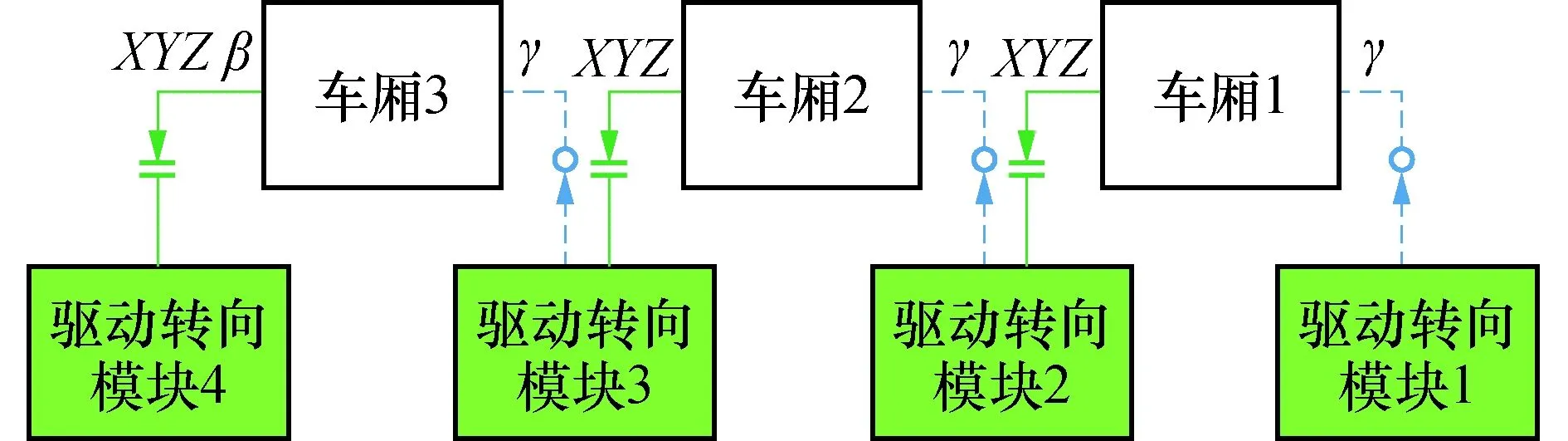
图2 驱动转向模块与车厢之间的拓扑结构图Fig.2 Topology diagram between drive steering module and carriages

车厢1与驱动转向模块1通过具有横摆γ相对转动自由度的铰接盘连接，并在车厢1与驱动转向模块2之间施加球铰约束，即约束纵向X、横向Y、垂向Z三个相对平动自由度，只保留相对转动自由度；其他车厢与其前后的驱动转向模块的拓扑连接方式与第1节车厢相同，另外最后一节车厢与最后的驱动转向模块之间在球铰约束的基础上还需约束俯仰β相对转动的自由度.

每个驱动转向模块的左右侧车轮均由轮边/轮毂电机独立驱动，使得各个驱动转向模块具有相对简易的机械结构. 仿真中设置的车厢、驱动转向模块和轮胎的主要参数如表1所示.

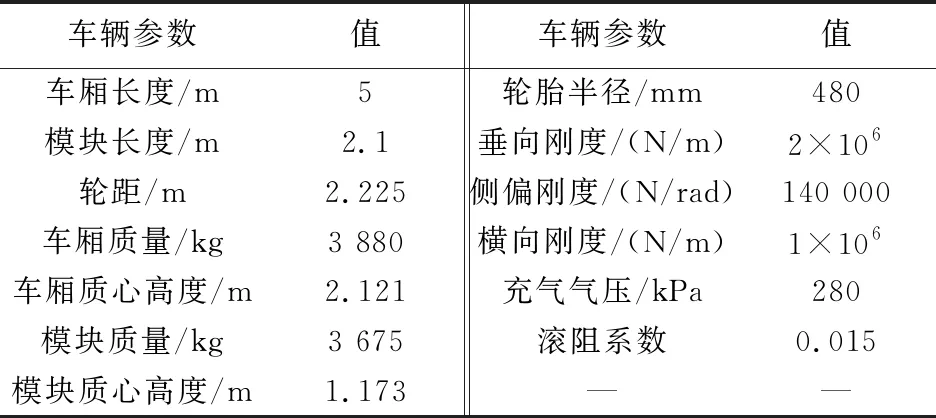
表1 多铰接虚拟轨道列车主要动力学参数Tab.1 Key dynamic parameters of the multi-axle virtual railway vehicle

2 基于单点预瞄的循迹控制

针对多铰接虚拟轨道列车，对每节车厢采用单点预瞄控制方法进行理论分析，并利用Simpack-Simulink软件展开联合仿真验证.

2.1 基于单点预瞄的循迹控制方法

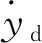
(1)

(2)

铰接点处的横向加速度可表示为

(3)

式中：R为车厢上铰接点处的转向半径.

根据前轮转向双轴车辆的运动学模型，小角度条件下的转向半径与前轮转角之间的关系为

δ=L/R

(4)

式中：L为轴距.

预瞄时间T后铰接点应行驶到预瞄点，故将横向位移等于预瞄横向偏差设置为控制目标，即

(5)

对于每一节车厢而言，其前方铰接的驱动转向模块相当于“前轴”，后方铰接的驱动转向模块相当于“后轴”. 由于“后轴”转角对车辆循迹效果产生的影响未知，故先不考虑车间铰接带来的各车厢间的运动耦合，直接对每节车厢应用单点预瞄循迹控制. 结合式(1)～(5)，可得到每节车厢前方驱动转向模块相对于该车厢的转向角目标值，前3个驱动转向模块的目标转角为

(6)

(7)

(8)

因第4驱动转向模块后方无车厢，用第4驱动转向模块相对第3车厢的转向角δ43来控制第4驱动转向模块的方向. 其转向角目标值构造为

(9)

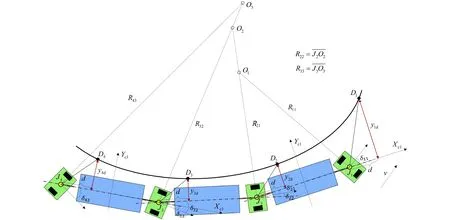
图3 多铰接虚拟轨道列车基于单点预瞄控制模型Fig.3 Multi-axle virtual railway vehicle model under single-point pre-targeting control

2.2 基于单点预瞄的循迹控制策略的仿真

每节车厢采取基于单点预瞄控制的循迹方法，将仿真工况设置为一段50 m直线，接半径为30 m的90°圆弧，再接50 m直线的目标轨道，车速设置为5 m/s,预瞄距离d=2 m，将虚拟轨道列车的起始位置距离道路中心线偏移量设置为0.5 m. 仿真中，虚拟轨道列车可以沿着圆弧曲线行驶，该工况下的仿真结果如图4所示.

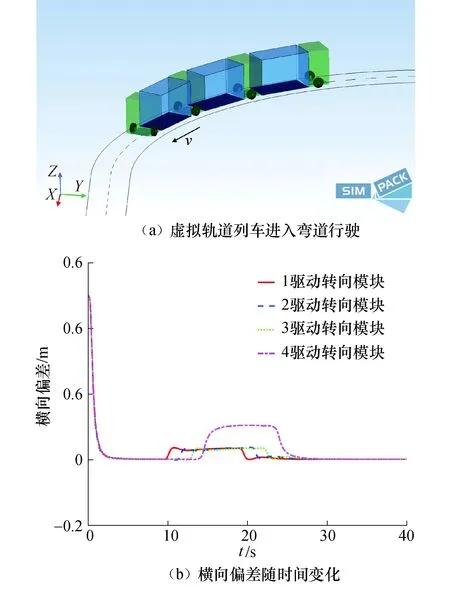
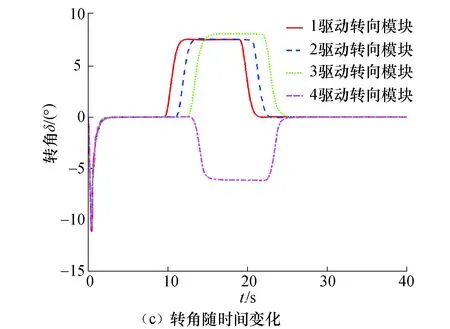
图4 基于单点预瞄的循迹控制策略的仿真结果Fig.4 Simulation results under single-point pre-targeting path-tracking control

在有0.5 m初始横向偏差的直线工况，参考图4(a)所示的坐标轴方向，4个驱动转向模块的转角在收敛到直线的过程中均为负. 10 s后进入曲线工况，前3个驱动转向模块的转角为正，第4驱动转向模块的转角为负. 实际上，对于除第1个驱动转向模块外的每个驱动转向模块，如果其相对于前车厢的转角固定为0，则退化为传统多铰接半挂车的形式，后轴有轨迹内移的趋势，对于图4(a)所示的横向方向，会有正方向的横向偏差. 如果每个驱动转向模块相对于前车厢的转角完全自由，则其在后车厢的惯性离心力作用下，会有向虚拟轨道外侧“外甩”的趋势，即对于图4(a)所示的横向方向，会有负方向的横向偏差. 横向循迹控制本质上就是在这两个趋势之间利用转角主动控制找到一个平衡，使其尽可能行驶在虚拟轨道上. 前3个驱动转向模块由于后方都铰接有车厢，横向惯性大，使得“外甩”的趋势相对较大，所以需要正打方向. 而第4个驱动转向模块由于后方没有车厢，受“后轴内移”趋势影响相对较大，所以需要反打方向.

由图4(b)和图4(c)知，在对虚拟轨道列车各个驱动转向模块直接应用单点预瞄控制的情况下，虚拟轨道列车可以快速纠正起始位置的横向偏移，并实现对目标轨道的跟随. 10 s之后，第1驱动转向模块进入弯道行驶，之后的驱动转向模块依次进入弯道. 在弯道行驶工况下，各驱动转向模块的横向偏移量均未收敛至0. 由此可见，不考虑各个驱动转向模块之间的力和运动的耦合关系，对各个驱动转向模块分别采用基于单点预瞄的循迹控制，虚拟轨道列车的弯道虚拟轨迹跟踪效果并不理想.

3 多轴协同预瞄循迹控制

将多铰接虚拟轨道列车的各个车厢和驱动转向模块间的运动和力的耦合关系考虑在内，结合单点预瞄原理可以提出应用于虚拟轨道列车的基于单点预瞄的多轴协同循迹控制方法，并利用Simpack-Simulink联合仿真对该控制方法的有效性进行验证.

3.1 多轴协同预瞄循迹控制策略原理

以第1节车厢为例，其运动规律由第1个驱动转向模块和第2个驱动转向模块相对于第1节车厢的转角决定，如图5所示.

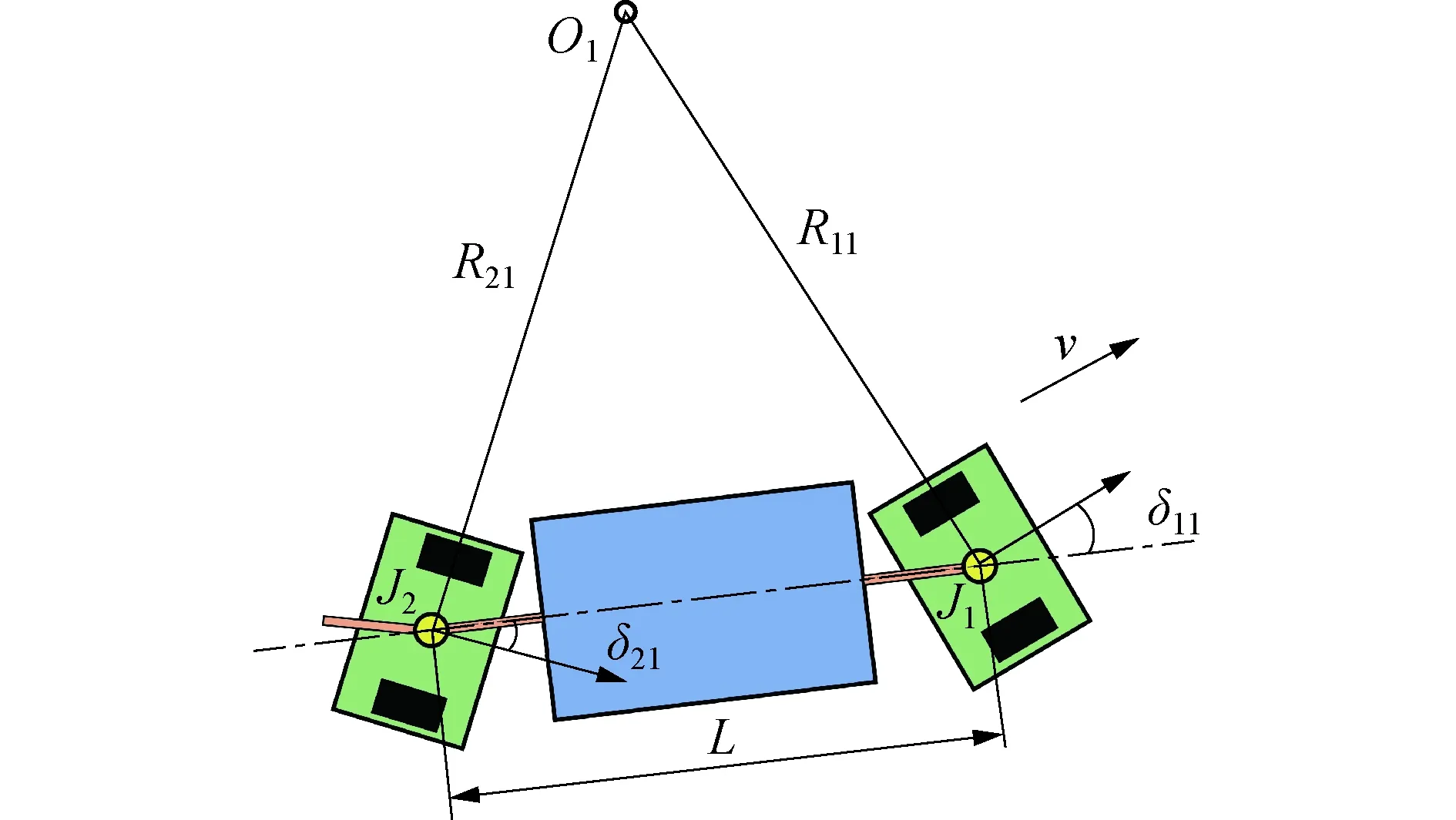
图5 第1节车厢与驱动转向模块间的运动学关系Fig.5 Kinematic model of the first carriage with its front and rear driving-steering integration modules

O1为第1节车厢前后两个驱动转向模块铰接点的瞬时转动中心，R11为该车厢上第一铰接点J1的转动半径，R21为该车厢上第二铰接点J2的转动半径，L为相邻两个铰接点之间的距离. 由于驱动转向模块和车厢在铰接处的速度相同，所以利用铰接点处，即J1和J2处的两个驱动转向模块的速度，即可确定出车厢的平面瞬时转动中心O1.

规定相对于车厢朝向的逆时针转向角方向为正方向，即图5情形下δ11为正，δ21为负. 根据正弦定理可得

(10)

整理得

(11)

在驱动转向模块相对于车厢的转角为小角度的条件下，可进行近似简化，cosδ11≈1，tanδ11≈δ11，tanδ21≈δ21，从而得到

(12)

在小角度条件下，R11与R21近似相等. 以R11近似作为第1节车厢的瞬时转动半径，则其横向加速度为

(13)

同理，第2、第3节车厢的横向加速度为

(14)

(15)

根据(13)式，结合第1节车厢前方铰接点处的横向加速度，即第一驱动转向模块铰接点的横向加速度，参考(1)式计算出该点在预瞄时间T后的横向位移为

(16)

经过前视时间T之后，为使该驱动转向模块中心行驶到目标轨迹上，须满足Δy1=y1d，即

(17)

由式(16)推导出第一个驱动转向模块铰接点相对第1节车厢的期望转角δ11d为

(18)

同理可得

(19)

(20)

对于第4驱动转向模块的转向控制，由于第4驱动转向模块后方无车厢存在，故类似前三个驱动转向模块的单点预瞄算法不适用于该驱动转向模块. 如果同时对驱动转向模块3和驱动转向模块4基于第2节车厢采用单点预瞄控制，则只能实现第3车厢横向偏移的控制. 因此考虑到对第3车厢横摆方向的控制，利用驱动转向模块4的转向实现对第3车厢横摆方向运动的控制. 第3车厢的角度偏差可表示为

(21)

如果可以控制车厢的横摆角速度为ωd，经过预瞄时间T后，第3车厢的横摆角度偏差应变为0，即

(22)

从而推算出第3车厢的目标横摆角速度为

(23)

在基于第3车厢前后驱动转向模块的小角度前提下，根据驱动转向模块的转角可以推知第3车厢的实际横摆角速度为

(24)

通过控制第4驱动转向模块的转向角使第3车厢达到目标横摆角速度，即

ω=ωd

(25)

则有

(26)

从而求出第4驱动转向模块的理论转向角为

(27)

3.2 多轴协同预瞄循迹控制策略仿真验证

对基于单点预瞄的多轴协同控制策略进行仿真验证时，由于驱动转向模块惯性较大，控制上存在一定的时间延迟，不能立即达到理论转角位置，需要用反馈控制进行动态调节以实现目标转向角. 采用PID控制器，将各个驱动转向模块与对应车厢间的实际转角与期望转角的偏差作为PID控制器的输入参数，将驱动转向模块两侧电机的电压差作为PID控制器的输出参数，控制器设计如图6所示. 其中PID控制器的参数分别设置为KP=60，KI=30，KD=20.

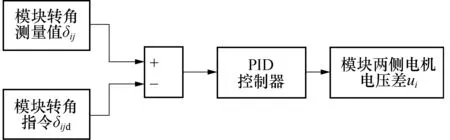
图6 各模块转角PID控制器设计Fig.6 PID-control-based actuator model of each driving-steering integration module

第4驱动转向模块控制第3车厢角度偏差的过程也利用PID控制方法进行动态调整. PID控制器设计如图7所示，输入包括第3车厢的角度偏差和第3驱动转向模块的转角测量值，输出为第4模块转角指令. 其中PID参数设置为KP=1，KI=1.7，KD=0.

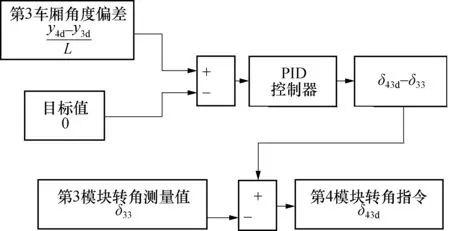
图7 第4驱动转向模块转角PID控制器设计Fig.7 PID-control-based steering angle command model of the last driving-steering integration module

由于两个PID底层控制器的目的只是让实际转角向目标转角收敛，并不需要调校至最优动态性能，只需将PID控制器调整到稳定的边界范围内，稍做调试优化，在一定程度上提升不同车速下的鲁棒性即可. 实施过程中，采用控制工程中的“试探法”[19]调整PID参数即足够.

仿真分析该工况条件下虚拟轨道列车的轨迹跟随效果，具体仿真结果如图8所示.

图8 多轴协同预瞄循迹控制下的仿真结果Fig.8 Simulation results under multi-axle cooperative control

图8(a)中多铰接虚拟轨道列车在基于单点预瞄的多轴协同循迹控制时，各驱动转向模块在弯道过程中的横向偏差较小，均可以收敛至0. 虚拟轨道列车在进入和驶出弯道过程中能够较快地跟随轨迹，使横向偏差达到收敛状态. 图8(b)中驱动转向模块的转角均在正常范围内.

对图8(b)和图4(c)在10 s之后的各驱动转向模块曲线对应时间作差，可以得到曲线工况下两种方法各驱动转向模块的转角差随时间的变化关系,如图9所示.

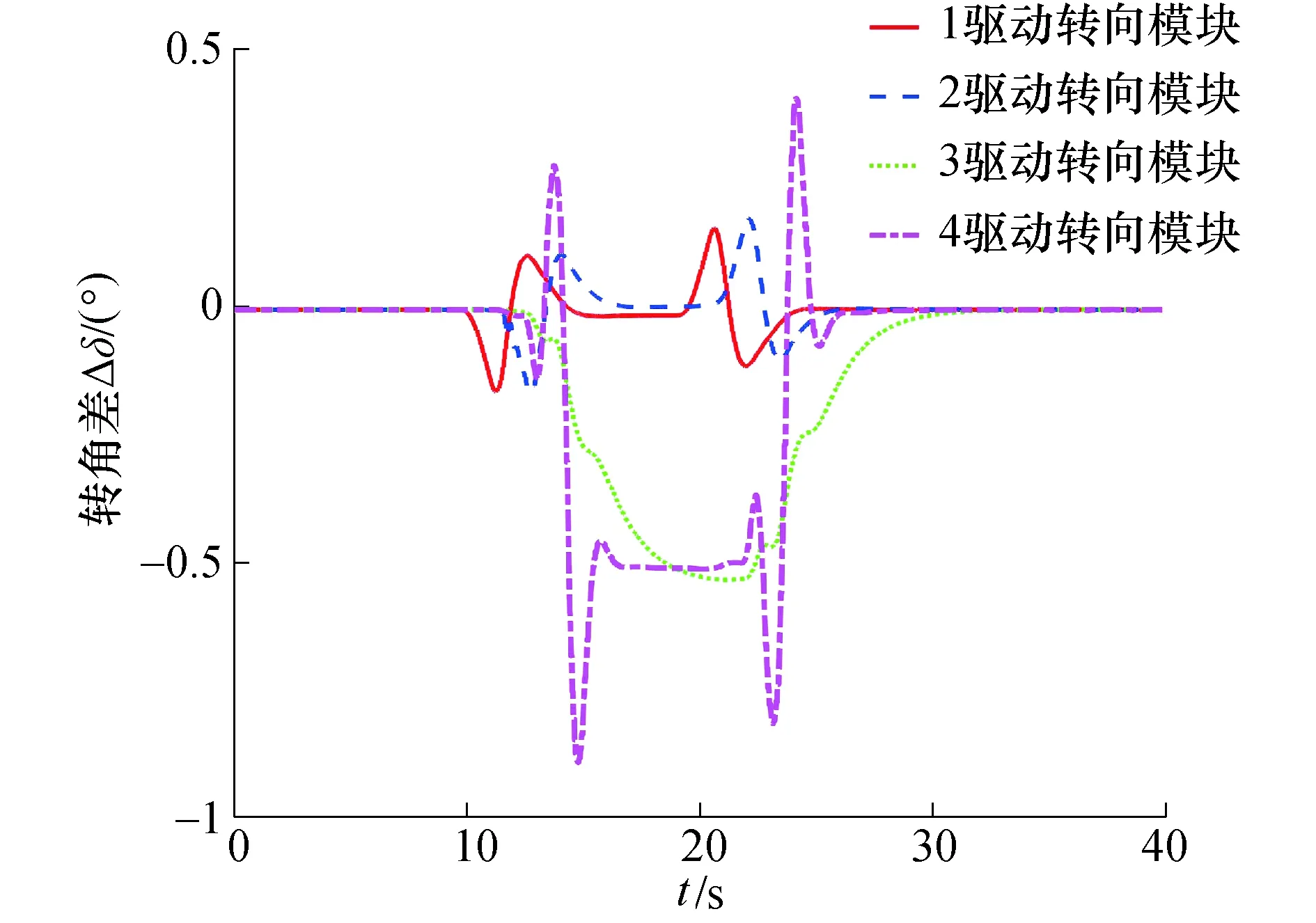
图9 曲线工况下两种方法各驱动转向模块的转角差随时间的变化关系Fig.9 Variation relation between the steering angle difference of each driving-steering integration module in the two methods with time on the curved track

由图9知，虽然转角差的绝对值不大，但是第4驱动转向模块相对其曲线工况下的最大绝对转角6.6°，有近10%的相对差别，使得第4驱动转向模块的循迹效果变好. 又由于基于图5的分析考虑到了各车厢前后两个驱动转向模块对车厢运动学的影响，进而在多轴协同的作用下，图8(a)相比图4(b)在曲线工况下整体的控制效果变好.

综合图8(b)和图9，前三个驱动转向模块的横向偏差变化规律一致，说明基于单点预瞄的多铰接虚拟轨道列车多轴协同循迹控制方法对不同驱动转向模块的控制具有一定的相似性. 第4驱动转向模块采用第3车厢转角偏差控制时，其在弯道处的横向偏差也较小，且能够收敛，验证了针对第4驱动转向模块控制方法的有效性. 曲线工况下4个驱动转向模块相对虚拟轨道的横向偏差均较小，且均能够收敛，验证了多轴协同预瞄循迹控制方法的有效性.

4 结论

1)针对特定结构的多铰接虚拟轨道列车行驶提出了一种基于单点预瞄的多轴协同循迹控制方法.相比于只基于单点预瞄的循迹控制方法，对于某一节车厢，需要考虑其后侧驱动转向模块的转角，以实现多轴协同控制.针对整车尾部驱动转向模块的特殊性，需让尾部驱动转向模块控制其所在车厢相对于目标轨道的角度偏差收敛，以保证其在曲线上的行驶稳定性并收敛至目标轨道.

2)基于多体动力学仿真软件Simpack搭建了多铰接虚拟轨道列车动力学模型，设计了多铰接虚拟轨道列车曲线运行工况，利用Simpack-Simulink软件联合仿真分别对四个驱动转向模块采用单点预瞄方法以及采用基于单点预瞄的多轴协同循迹控制方法进行了仿真验证. 通过对比两种控制方法下多铰接虚拟轨道列车的横向偏差仿真结果，证明了基于单点预瞄的多轴协同循迹控制方法能够显著改善虚拟轨道列车通过弯道时后轴轨迹内移现象，提高虚拟轨道列车的循迹能力，进而提升虚拟轨道列车弯道行驶的安全性和机动性.