基于正交试验的发动机定位力改进分析

孙芸　张洪信　赵清海

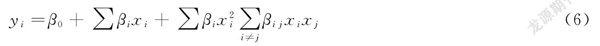
文章编号： 10069798（2022）01008006; DOI： 10.13306/j.10069798.2022.01.012

摘要：  针对双元动力发动机存在的结构复杂和非线性磁路难以建立精确优化模型等问题，本文基于正交试验，对永磁活塞机械电力发动机定位力进行改进分析。研究了永磁体沿磁化方向长度、气隙宽度、齿槽槽宽对定位力的影响，利用正交试验法对各参数进行优化，并以定位力幅值最小为目标，得到发动机电动力结构的最优尺寸，同时对仿真结果进行极差分析，得到主要结构参数对目标值影响的权重顺序。分析结果表明，优化后定位力幅值为507 N，与优化前相比，降低了489%，验证了优化方法的有效性，有效改进了永磁活塞机械电力发动机结构的定位力。该研究为永磁活塞机械电力发动机的设计优化提供了理论依据。

关键词：  发动机; 直线电机; 正交试验; 定位力

中图分类号： TM351文献标识码： A

永磁活塞机械电力发动机将传统发动机与直线电机集成一体，是一种高度紧凑的双元动力装置，其直线电机部分的定位力，对整个系统的稳定运行具有重要作用。目前，电磁力波动是直线电机在实际应用中的主要缺陷之一，因此学者们运用多种方法进行相關研究。S.ARSLAN等人[1]通过对设计变量建立响应面模型，确定设计变量和发电机输出变量大小之间的关联，进而利用多目标遗传算法，找出结构尺寸的最优值，有效提高直线发电机效率，减少定位力波动，实现提高综合性能的目标;ZHANG W J等人[2]采用模型参考自适应控制（model referenced adaptive control，MRAC）和周期自适应学习控制（periodic adaptive learning control，PALC）算法，提出了一种消除重复运动任务下，力脉动对系统性能影响的补偿方法，有效减小了永磁直线同步电机（permanet magnent piston mechanical power engine，PMPMPE）的力脉动;胡致远[3]引入全局优化算法，以电机结构参数作为优化变量，以电机平均水平推力和推力脉动幅值作为优化目标，寻找最优组合，并与田口法寻优进行比较，验证了全局优化算法的优良性能;宗开放[4]采用蚁群算法，对V型线圈双次级无铁芯永磁同步直线电机的相关结构参数优化迭代，得到一组最优的结构参数，实现推力波动最小的目标;赵玫等人[5]以推力密度、推力波动为优化目标，对聚磁式横向磁通永磁直线电机的优化变量进行灵敏度分析，实现了电负荷和磁负荷的解耦，并基于三维有限元法对所优化电机的定位力、电磁力等电磁性能进行计算与分析，验证了多目标优化设计方法的有效性;吴涛等人[6]应用一种改进的黑洞多目标进化算法，建立电机推力、推力体积比和铜损多目标优化模型，实现对圆筒型无槽无铁心直线永磁同步电机的多目标优化设计。基于此，本文将有限元与正交试验算法相结合，对永磁活塞机械电力发动机电动力结构的定位力进行改进分析。该研究为进一步完善永磁活塞机械电力发动机的电动力结构，减小定位力波动幅值提供了理论参考。

1永磁活塞机械电力发动机电动力结构定位力分析

永磁活塞机械电力发动机是将传统的活塞式内燃机与直线电机集成一体，其包括曲柄连杆机构、活塞

永磁铁动子组件（动子永磁体通过螺栓连接在活塞裙部）、定子组件（铁心和线圈）等。发动机工作时，活塞永磁铁动子组件做上下往复直线运动，并通过曲柄连杆机构驱动附属机构。电磁线圈内部磁通量因永磁体的往复运动发生变化，产生感应电动势，并对外输出电能。同时，曲轴端部仍可对外输出机械动力，满足多元动力需求。永磁活塞机械电力发动机外形结构如图1所示，该发动机为二冲程发动机，曲柄连杆机构上下运动1个周期的时间约为18 ms。

由于电动力结构存在端部效应和齿槽效应，使永磁活塞发动机存在定位力波动。定位力对永磁活塞机械电力发动机的性能影响较大，使电机的电磁推力发生波动。如果定位力过大，则电磁力波动较大，进而产生振动以及噪声。当发动机低速运行时，有可能引起共振，影响发动机安全稳定运行，为提升电动力结构的性能，必须尽可能的减少定位力[710]。

永磁活塞机械电力发动机电动力结构的定位力包括边端力和“齿槽”定位力。其中，边端力沿轴向端方向，在运动过程中，动子永磁体磁钢产生推力波动，在分析端部磁通变化规律的基础上，得到端部推力波动为

式中，Kc为卡式系数;δ为气隙长度;Φm为最大磁通幅值;μ0为真空磁导率;k为磁通压缩系数;τ为极距;l为铁心厚度;n为槽数。

“齿槽”定位力是由于铁心处气隙磁场分布不均匀产生的一种周期性脉动电磁力，本质上是由定子“齿槽”与动子永磁体相互作用而产生。采用虚位移法，对“齿槽”定位力进行解析计算，假设动子沿着x方向有位移，此时运动物体受力计算公式为

磁场能量为

式中，L和D分别为永磁活塞机械电力发动机电动力结构初级长度和次级外径;Br为磁钢剩磁;δ（θ，α）为气隙有效长度;h为永磁体充磁方向长度。

运用傅里叶展开式，得电动力结构的“齿槽”定位力为

定位力为

2电动力结构参数对定位力的影响

2.1永磁体沿磁化方向长度

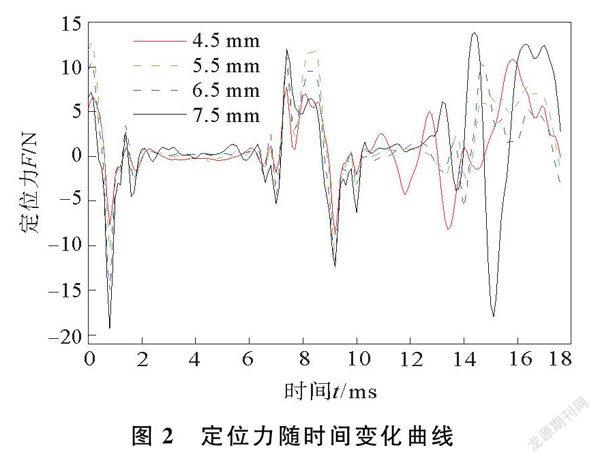
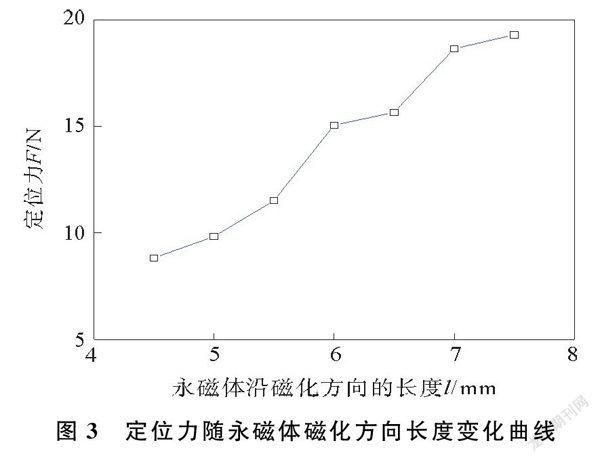
改变永磁体轴向长度，即永磁体磁化方向长度，当永磁体磁化方向长度不同时，定位力随时间变化曲线如图2所示，定位力随永磁体磁化方向长度变化曲线如图3所示。由图2和图3可以看出，随着永磁体磁化方向长度的逐渐增大，由45 mm变化到75 mm，电动力结构的定位力幅值不断增大。这是由于随着永磁体磁化方向长度增大，电动力结构内的气隙磁密不断增大，而定位力的大小与电机气隙磁密的平方成正比，因此定位力的幅值不断增大。且增大的速率趋于平缓。

2.2气隙宽度

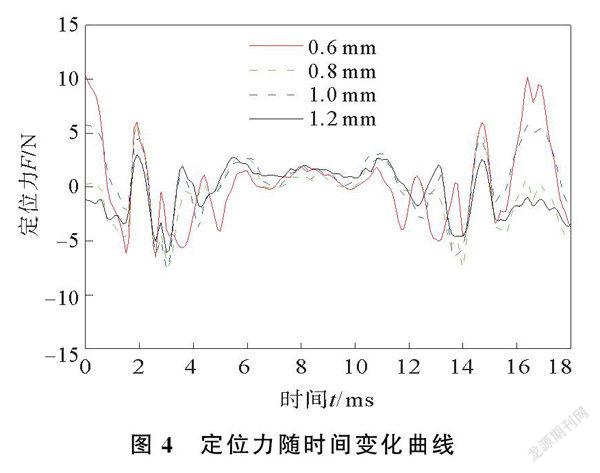
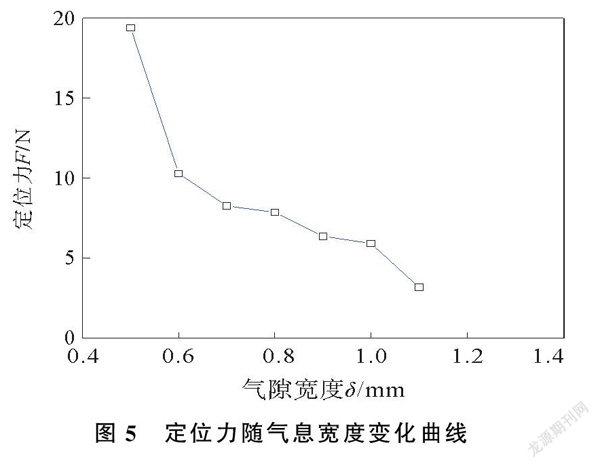
在不同氣隙宽度下，定位力随时间变化曲线如图4所示，定位力随气息宽度变化曲线如图5所示。由图4可以看出，气隙宽度由06 mm增加到12 mm，对应定位力幅值随气隙宽度的增大而减小。由图5可以看出，电动力结构的定位力与磁感应强度呈正相关，气隙宽度越大，磁感应强度越小，定位力幅值也就越小。

2.3齿槽槽高

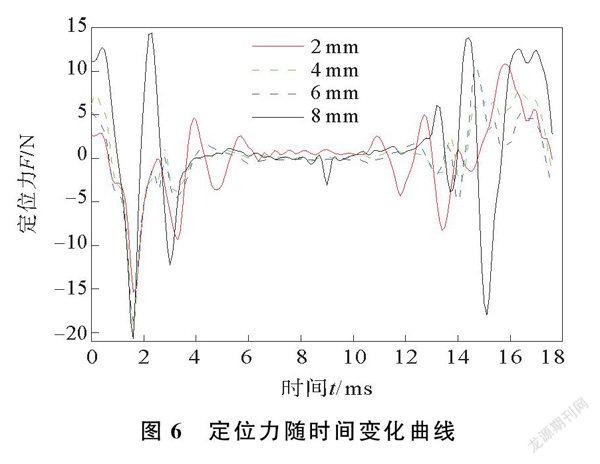
为有效降低铁心损耗，永磁活塞机械电力发动机电动力结构部分的定子铁心由硅钢片叠加组成，定子叠片轴向长度不仅对定位力大小有较大影响，而且还影响定位力的波形。在不同齿槽槽高度条件下，定位力随时间变化曲线如图6所示，定位力随齿槽高度变化曲线如图7所示。由图6可以看出，电动力结构的定位力幅值随定子叠片单元轴向长度的变化先减小后增大，这与传统永磁同步电机的定位力矩幅值随定子齿宽的变化规律基本一致。由图7可以看出，齿槽槽高的变化改变了发动机电动力结构的气隙磁导，导致变化率不同。当气隙磁导变化率减小时，电机的边端效应减弱，定位力减小。

3正交试验设计与优化分析

3.1正交试验设计

当多个因素同时变化时，正交试验法可同时对多个元素进行分析，通过较少的试验次数，找到最优的参数组合，从而减少工作时间，提高设计效率，而ISIGHT集成设计优化框架在这方面具有较强的功能[1116]。参照上述各参数对定位力的影响程度，选择沿永磁体充磁方向的长度l、气隙宽度δ和齿槽槽高h作为优化变量，建立优化模型，对目标值进行优化。优化变量示意图如图8所示。

基于ISIGHT集成ANSOFT Maxwell有限元软件，采用正交试验算法，构建正交数组，降低永磁活塞机械电力发动机电动力结构的定位力波动幅值。根据前述所求得的定位力随试验因素的变化情况，确定正交试验因素水平的选取范围，正交试验因素水平及试验因素如表1所示。

根据试验因素及因素水平，确定正交表为L16（43），即试验包括3个因素，每个因素有4个不同的值，共进行16次试验，正交表和试验结果如表2所示。

3.2正交试验结果

3.2.1变量对响应的贡献

ISIGHT根据样本点建立多元二次回归模型，通过回归系数进行表达[1719]，回归系数表如表3所示。表中的参数反应多项式模型中每一项对响应的主效应，因子对响应的主效应是因子在某个水平时所有试验中相应的平均值;表中的系数是将模型系数转化为贡献率百分比，描述各变量对结果的贡献值。

回归系数为

式中，yi为上述响应;xi为上述因子;βi为对应因子项对响应的贡献率。

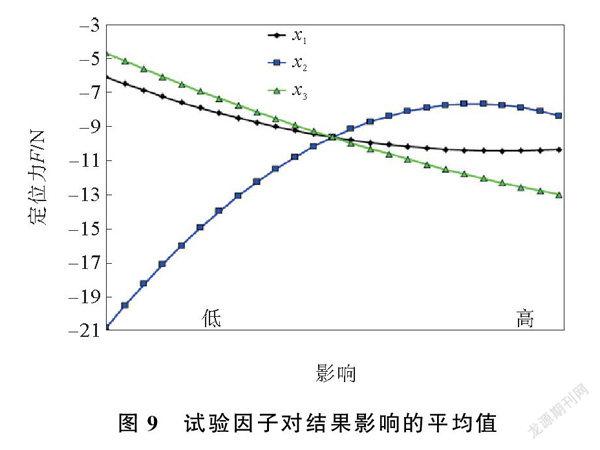
试验因子对结果影响的平均值如图9所示，由图9可以看出，随着定位力绝对值（负号仅代表方向）不断减小，变量气隙宽度x2的影响逐渐增大，而沿永磁体磁化方向的长度x1和槽高x3的影响逐渐减少。

Pareto图可直观反映回归模型中各因子项对响应的贡献率，其值为系数表中的规范化值[20]。样本拟合后，模型中所有项对每个响应贡献程度百分比如图10所示。图10中，蓝色条形表示正效应，即参数越大，越接近目标值;红色表示反效应;平方项代表该参数对目标值特征的影响，具有非线性。由图7可以看出，x2对目标值的贡献率最大，且为正效应，而x1和x3为反效应。

3.2.2试验结果分析

用极差法对正交实验结果进行分析，根据正交试验结果，求出每个因素在每个水平的平均值，即

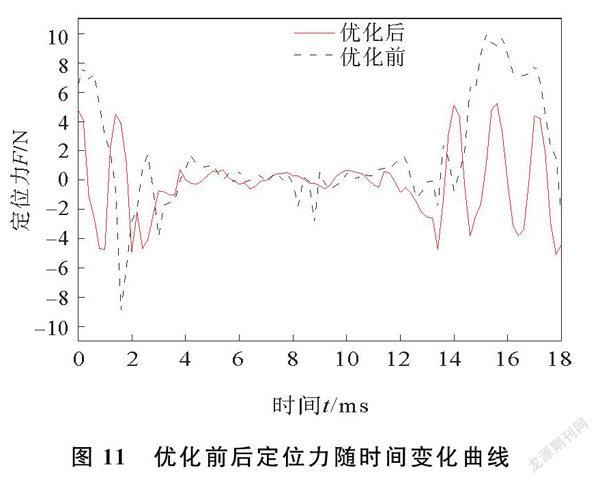
基于优化后得到的参数组合，建立三维有限元模型，对电动力结构进行仿真分析，优化前后定位力随时间变化曲线如图11所示。由图11可以看出，优化前的定位力波动幅值为992 N，优化后为507 N，与优化前相比，降低了489%，有效改进了永磁活塞机械电力发动机电动力结构的定位力。

正交实验结果分析如表4所示。由表4可以看出，对于定位力幅值，根据极差大小可得到因素的主次顺序为l，δ，h。考虑定位力幅值越小越好，选出最优因素的水平组合l（2）δ（2）h（1），即沿永磁体充磁方向的长度为5 mm，气隙高度为07 mm，槽高为5 mm。

4结束语

本文以新式双元动力发动机——永磁活塞机械电力发动机为研究对象，通过建立三维模型，叙述其基本结构和工作原理，并对其定位力进行解析。采用有限元法对发动机电动力结构进行电磁分析，得到在不同参数下的定位力波形，通过分析永磁体沿磁化方向长度、气隙宽度和齿槽槽高对电动力结构中定位力的影响，获得定位力随时间的变化规律，从而求得参数的最优尺寸。同时，利用正交试验法对发动机电动力结构进行优化，以上述变量为优化变量，以定位力波动幅值最小为目标，得到电动力结构的最优尺寸，并确定电动力结构沿永磁体充磁方向的长度为5 mm，气隙宽度为07 mm，齿槽槽高为5 mm为最优参数组合，优化后电动力结构的定位力赋值为507 N，与优化前相比降低了489%。但在研究过程中未考虑温度对发动机电动力结构的影响，后期还需进一步探索。

参考文献：

[1]ARSLAN S， GRDAL O， OY S A. Design and optimization of tubular linear permanent magnet generator with performance improvement using response surface methodology and multiobjective genetic algorithm[J]. Scientia Iranica， 2018， 27（6）： 30533065.

[2]ZHANG W J， NAN N， YANG Y F， et al. Force ripple compensation in a PMLSM position servo system using periodic adaptive learning control[J]. ISA transactions， 2019， 95： 266277.

[3]胡致远. 基于全局优化算法MVO的永磁同步直线电机的优化设计[D]. 广州： 华南理工大学， 2019.

[4]宗开放. 基于V型线圈永磁同步直线电机推力波动抑制研究[D]. 合肥： 安徽大学， 2020.

[5]赵玫， 于帅， 邹海林， 等. 聚磁式横向磁通永磁直线电机的多目标优化[J]. 电工技术学报， 2021， 36（17）： 37303740.

[6]吴涛， 商慧丽， 张煜葵， 等. 基于黑洞多目标进化算法的永磁直线同步电机优化设计研究[J/OL]. 控制与决策， 2021： 16[20210506]： https： ∥doi. org/10. 13195/j. kzyjc. 2020. 0869

[7]WANG W J， ZHAO J， SONG J， et al. Thrust performance improvement for pmslm through doublelayer reverse skewed coil and wrfmkh method[J]. IEEE/ASME Transactions on Mechatronics， 2020， 25（6）： 29502960.

[8]ISAZA C V， SARMIENTO H O， KEMPOWSKYHAMON T， et al. Situation prediction based on fuzzy clustering for industrial complex processes[J]. Information Sciences， 2014， 279： 785804.

[9]DONG F， ZHAO J W， ZHAO J， et al. Robust optimization of pmlsm based on a new filled function algorithm with a sigma level stability convergence criterion[J]. IEEE Transactions on Industrial Informatics， 2020， 99： 11.

[10]AYALA H V H， SEGUNDO E H V， MARIANI V C， et al. Multiobjective krill herd algorithm for electromagnetic optimization[J]. IEEE Transactions on Magnetics， 2016， 52（3）： 72085047208507.

[11]李佳霖， 李劲松， 李美. Isight平台理论与方法及其在产品结构设计与优化中的应用研究[J]. 汽车实用技术， 2021， 46（8）： 6367.

[12]陈昭明， 邹劲松， 王伟， 等. 改进粒子群神经网络融合有限元分析的铸锻双控动态成型多目标优化[J/OL]. 吉林大学学报（工学版）， 2021： 111. https：∥doi. org/10.13229/j.cnki.jdxbgxb20210108.

[13]黄国富， 张乔宇. 船型小样本结合近似模型的阻力性能优化[J]. 船海工程， 2020， 49（3）： 5358.

[14]ZHAO W X， YAO T， XU L， et al. Multiobjective optimization design of a modular linear permanentmagnet vernier machine by combined approximation models and differential evolution[J]. IEEE Transactions on Industrial Electronics， 2020， 68（6）： 46344645.

[15]HWANG C C， LI P L， CHUANG F C， et al. Optimization for reduction of torque ripple in an axial flux permanent magnet machine[J]. IEEE Transactions on Magnetics， 2009， 45（3）： 17601763.

[16]HASANIEN H M. Particle swarm design optimization of transverse flux linear motor for weight reduction and improvement of thrust force[J]. IEEE Transactions on Industrial Electronics， 2011， 58（9）： 40484056.

[17]彭显刚， 林利祥， 刘艺， 等. 基于纵横交叉-拉丁超立方采樣蒙特卡洛模拟法的分布式电源优化配置[J]. 中国电机工程学报， 2015， 35（16）： 40774085.

[18]史石磊， 康尔良， 史桂英. 扁平型永磁直线电机定位力综合优化[J]. 微电机， 2020， 53（3）： 3337， 54.

[19]胡凯. 自由活塞内燃发电机系统中直线电机的研究[D]. 上海： 上海交通大学， 2018.

[20]施小娟， 吉洪湖. 二元收扩喷管设计参数对红外特征影响的数值研究[J]. 航空动力学报， 2020， 35（5）： 944955.

Improved Analysis of Positioning Force of Permanent Magnet Piston

Mechanical Electric Engine Based on Orthogonal TestSUN Yun ZHANG Hongxin ZHAO Qinghai

（a. College of Mechanical and Electrical Engineering;  b. Power Integration and

Energy Storage Systems Engineering Technology Center， Qingdao University， Qingdao 266071， China）Abstract：  Aiming at the problems of complex structure and nonlinear magnetic circuit that are difficult to establish an accurate optimization model of the dualelement power engine， this paper improves the analysis of the positioning force of the permanent magnet piston mechanical electric engine based on orthogonal tests. The effects of the length of the permanent magnet along the magnetization direction， the air gap width and the slot width of the tooth slot on the positioning force are investigated， and the orthogonal test method is used to optimize each parameter to obtain the optimal size of the engine electrodynamic structure with the minimum positioning force amplitude as the target， while the extreme difference analysis is performed on the simulation results to obtain the weight order of the influence of the main structural parameters on the target value. The analysis results show that the optimized positioning force amplitude is 5.07 N， which is 48.9% lower than that before optimization， verifying the effectiveness of the optimization method and effectively improving the positioning force of the permanent magnet piston mechanical electric engine structure. This study provides a theoretical basis for the design optimization of the permanent magnet piston mechanical electric engine.

Key words： engine; Linear motor; orthogonal test; positioning force

收稿日期： 20210901; 修回日期： 20211103

基金項目：  国家自然科学基金资助项目（52075278）; 青岛市民生科技计划项目（196192nsh）

作者简介：  孙芸（1997），女，硕士研究生，主要研究方向为车辆新型动力传动技术及其电子化。

通信作者：  张洪信（1969），男，教授，博士，主要研究方向为动力系统集成仿真匹配及多学科设计优化。 Email： qduzhx@126.com