复杂山地大跨多曲拱-斜柱结构设计与分析

2022-03-24刘向刚陈剑峰赵雪冰郑良平来武清

工业建筑 2022年12期

刘向刚陈剑峰杨越赵雪冰郑良平来武清

(中机中联工程有限公司，重庆 400039)

山地建筑依照坡度差异进行建筑布局，并与山地地形地貌相协调以减少对坡地的高挖或高填，取得错落有致的建筑效果[1]。近年来，为了使建筑与山地自然景观相协调，大量异形复杂建筑被广泛运用于山地自然景观区域，而这些异形复杂建筑难以用常规的掉层或吊脚框架结构实现[2-3]。为此，基于重庆中岛艺路项目中的异形复杂建筑提出了大跨多曲拱-斜柱结构方案，既能满足异形建筑造型的需求，又能解决异形复杂建筑跨越复杂山地的难题。通过时多曲拱倾斜角度、斜柱倾斜角度、弧形撑位置等参数对大跨多曲拱-斜柱结构体系影响的分析，并根据分析结果确定了最终结构方案。基于最终大跨多曲拱-斜柱结构方案，分析了结构受力、结构变形、结构稳定、结构地震时程响应和抗连续倒塌等内容，并根据结构分析内力对多曲拱铸钢节点进行了有限元分析。对此类结构的舒适度进行了详细分析，并对结构的基础和拱脚连接进行了详细介绍。

1 工程介绍

1.1 工程概况

重庆中岛艺路项目位于重庆九龙坡区长江艺术湾区美术公园入口段处，上连杨家坪商圈，下接涂鸦街。该项目为重庆美术公园提供了一个兼具美术信息传播、休憩观景、艺术创作基地的城市空间。项目全长约1.5 km，其后侧是杨九路，其正前方约300 m处是长江，其中风憩阁为一栋单层建筑，建筑总面积约1 131 m2，其屋面为斜屋面，最高点为6.5 m，最低点为4.3 m，主要功能为艺术展览和休憩观景。风憩阁建筑造型突破常规，多重曲面的流线型造型构建成复杂的空间体系，建筑平面似月牙形，其立面由空间多曲拱和弧形斜撑形成视野开阔的弧形曲面，整个结构形态就是建筑形态本身(图1)。

a—建筑效果；b—建筑室外；c—建筑室内。图1 建筑效果及实景Fig.1 Rendering and the actual building

1.2 工程难点

该异形建筑展现曲线之美的同时给结构带来了巨大的挑战，主要体现在以下三点：1)建筑造型多曲流线型，内部需要大空间，建筑内部不能设置结构柱，使建筑跨度大，常规框架结构难以实现。2)由于建筑正前方是长江，建筑外立面要求视野开阔，致使建筑外侧不能设置常规跨度的结构柱。3)建筑位于陡坡上，总体地形坡度为50°～85°，部分区域达到90°(图2)，基础设置困难。

a—结构与边坡关系;b—典型地质剖面。图2 结构与地形关系Fig.2 Relations between the building and the terrain

1.3 设计条件

结构设计使用年限为50年，安全等级为二级，设防类别为标准类，抗震设防类烈度为6度，设计地震分组为第一组，场地类别为二类，场地特征周期为0.40 s。根据GB 50011—2010《建筑抗震设计规范》[4]，考虑边坡不利影响，地震放大系数取1.6。采用振型分解反应谱法计算地震响应。恒荷载包括：1)重力荷载，软件自动计算，并且考虑1.05的放大系数；2)屋面附加恒载7.0 kN/m2，一层附加恒载3.0 kN/m2；3)玻璃幕墙按1.5 kN/m2面载考虑，折算成线荷载施加于梁上；4)栏杆恒载1.0 kN/m。活荷载包括：1)屋面及一层取4.0 kN/m2；2)栏杆竖向荷载取1.2 kN/m。对于风荷载，基本风压为0.40 kN/m2(50年一遇)，场地粗糙度类别为B类。对于温度作用，考虑结构合龙温度为15～25 ℃，升温30 ℃，降温25 ℃。

2 结构方案

2.1 结构方案选择

如何解决该异形复杂建筑跨越复杂边坡成为本工程的难题。为了解决这种地形条件下竖向力传递问题，同时满足建筑大开间、大视野需求，结构采用多曲拱、弧形撑和斜柱形成中间无柱的复杂钢结构受力体系(图3a)。结构体系中多曲拱倾斜一定角度的主要原因是：如果多曲拱不倾斜，拱脚在斜坡边缘，将无法设置拱脚基础(图2)。结构在主要受荷模式竖向荷载作用时(图3b)，整体结构有向外倾覆的趋势，致使多曲拱以受压力、弯矩和扭矩为主，与多曲拱相连的楼层梁起到拉杆作用，楼层梁将拉力传递给后排柱。为了增加结构的抗倾覆能力，主要采取两项措施：1)后排柱采用斜柱以抵抗由拉拱梁产生的水平拉力，并在柱脚处设置预应力锚索，以平衡斜柱在柱脚对桩产生的水平力推力；2)多曲拱拱脚段采用钢管混凝土组合拱以提高拱的安全储备。

a—结构侧视图；b—荷载传递途径。图3 结构方案Fig.3 Structural schemes

为了分析斜柱倾斜角度θ(图3b)对结构的有利作用，建立了两种结构对比模型，如图4所示，方案1后排柱倾斜角度θ为0°，方案2后排柱倾斜角度θ为15°，方案1和方案2除了后排柱倾斜角度不同外，其余结构布置均相同。由于结构的主要受荷模式为竖向荷载，因此，仅以方案1和方案2在恒载和活载作用下的受力和变形来分析后排柱倾斜角度θ对结构的影响。

a—方案1;b—方案2。图4 结构方案对比模型Fig.4 Comparisons of models between structural schemes

图5a为结构在“恒载+活载”作用下水平位移，方案1拱顶A点的水平位移约为方案2的1.11倍，说明后排柱倾斜可以增加结构的整体刚度。图5b为方案1与方案2在“1.3恒载+1.5活载”作用下内力分布，方案1多曲拱的最大弯矩、最大轴力和最大扭矩均大于方案2，说明后排柱倾斜对结构受力有利。综上可知，后排柱倾斜对结构刚度和受力均有利，因此，在空间条件允许的情况下应尽量增加后排柱的倾斜角度。

a—水平位移，mm;b—弯矩分布,kN·m。图5 结构方案位移和内力对比Fig.5 Comparisons of displacements and internal forces between different structural schemes

2.2 结构布置

基于结构方案分析结果，多曲拱的倾斜角度根据边坡条件进行调整确定，后排斜柱的倾斜角度根据柱顶和柱底距离已建挡墙一定距离进行调整。最终钢结构布置如图6所示，多曲拱的倾角为41°，后排斜柱的倾斜角度为15°。图6a、b为结构平面布置，钢梁、斜柱、弧形撑和多曲拱均采用箱型截面，各构件编号对应的截面尺寸见表1，钢材均为Q355B，多曲拱和斜柱GZ1在一层以下部分均采用钢管混凝土柱进行加强，钢管内浇灌C50微膨胀自密实混凝土。如图6c结构模型所示，GL2、GL3、GL4、弧形撑和多曲拱在一层相连形成复杂节点，采用铸钢节点进行设计。拱顶至一层的高度约为6.5 m，一层至拱脚的高度约为7.2 m，铸钢节点之间距离约为30 m，拱脚之间距离约为41 m，一层至屋面部分拱的矢跨比约为0.217，整个多曲拱的矢跨比为0.334。

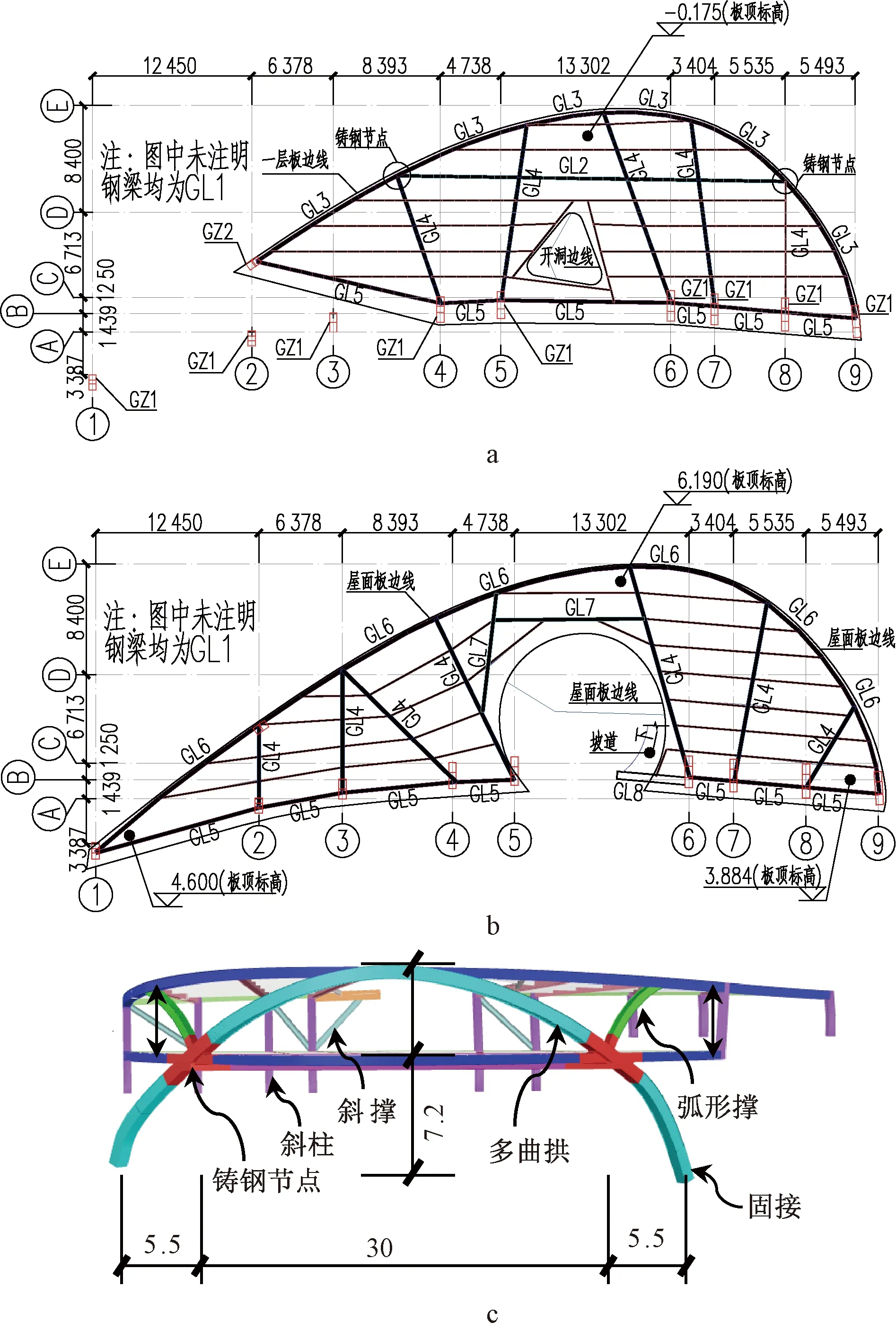
a—一层平面布置,mm；b—屋面平面布置,mm；c—结构模型,m。图6 结构布置Fig.6 The layout of the structure

表1 构件截面Table 1 Sections of members

3 结构分析

3.1 结构动力特征

振型数量取60，X、Y向振型质量参与系数为95%，满足规范[4]要求。图7为结构前4阶振型，均表现为以竖向振动为主，未出现水平振型，说明结构的抗侧刚度较大。结构前4阶振型对应的周期及频率见表2。

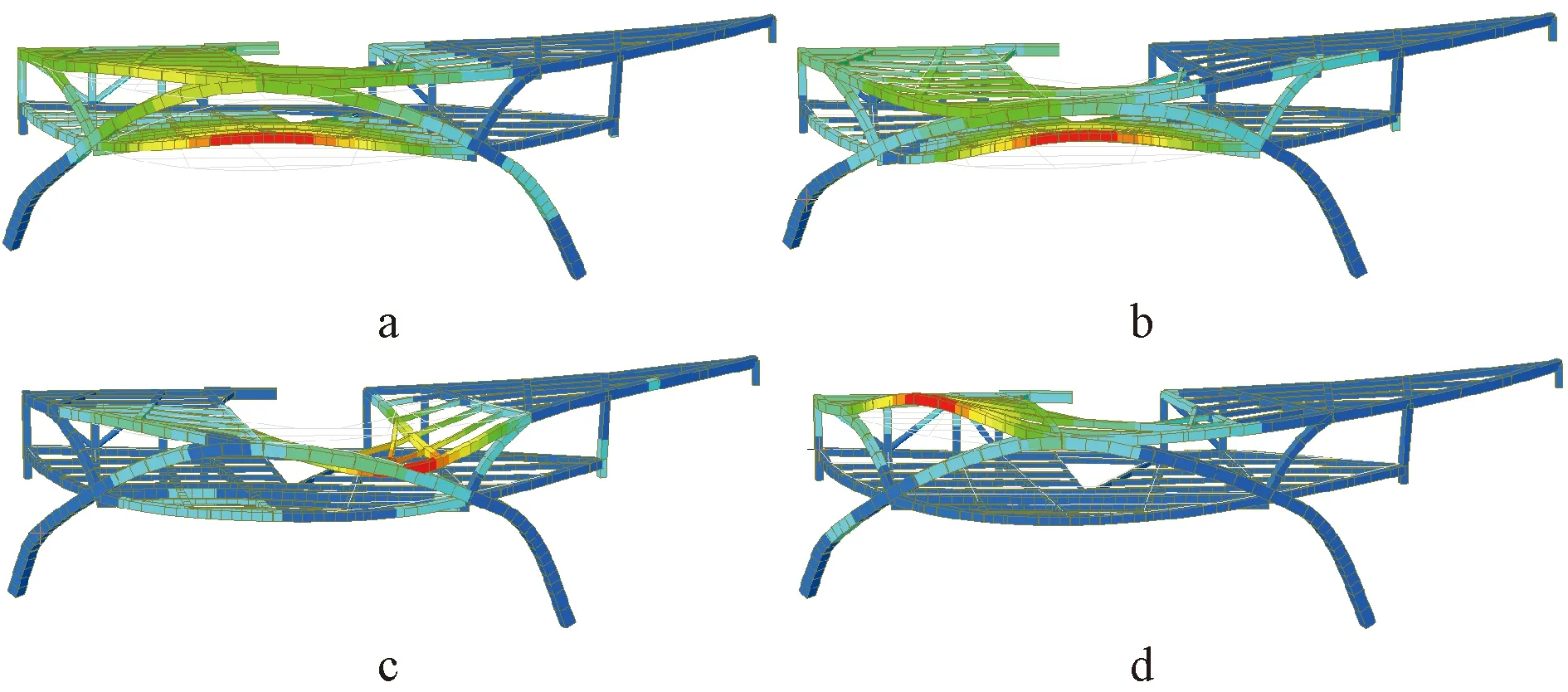
a—第一阶振型；b—第二阶振型；c—第三阶振型；d—第四阶振型。图7 前4阶振型Fig.7 The first fourth-order vibration modes

表2 前4阶振型周期Table 2 The first fourth-order vibration modes

3.2 结构位移

图 8a为1.0恒载+1.0活载作用下结构竖向位移，一层竖向变形最大，GL2跨中A点(图8a)的竖向位移为60 mm，小于限值75 mm(30 000/400)，悬挑区域B点(图7a)的最大竖向位移为95 mm，相对竖向位移为35 mm，小于限值44 mm(5 540/125)。图 8b分别为多遇地震下、风荷载下结构的水平位移，最大水平位移分别为1.4 mm、0.8 mm，对应位移角分别为1/4 643、1/8 125，均远小于规范[4]限值1/250。

a—竖向位移；b—水平位移。图8 结构位移 mmFig.8 Structural displacements

3.3 结构内力分析

图9为结构轴力、弯矩分布，表3为单工况下多曲拱、弧形撑、斜柱等主要构件的最大弯矩和轴力，可以看出，各主要构件的弯矩和轴力在恒荷载、活荷载及温度作用下较大，在多遇地震和风荷载作用下内力均较小。由此可见，恒载、活载及温度对结构起控制作用，荷载组合时应重点关注这些工况参与的组合。在竖向荷载作用下，GL3、GL4(图6)的轴力均为拉力，这与结构方案原理一致。

表3 各工况下主要构件内力Table 3 Internal forces of main members in different cases

a—恒载下;b—升温下。图9 单工况下内力Fig.9 Internal forces in single one cases

在恒荷载、活荷载及温度作用时，拱脚段是多曲拱受力最大的部位，其轴力和弯矩均达到最大。在恒荷载和活荷载作用下，拱顶扭矩达到最大，分别为843,242 kN·m，在温度作用下，拱脚扭矩达到最大239 kN·m。综上可知，多曲拱受力复杂，且为整个结构的关键构件，因此，多曲拱设计时有两方面需要重点关注，一是多曲拱构件稳定验算；二是多曲拱的节点和拱脚。对于节点，最重要的就是GL2、GL3、GL4、弧形撑与多曲拱相连形成复杂空间节点(图6c)；对于拱脚，其轴力、弯矩和扭矩均很大，是结构设计的关键部位，因此，铸钢节点至拱脚范围的多曲拱采用钢管混凝土组合拱进行加强，并采用埋入式柱脚方式连接。

轴力负号表示受压，正号表示受拉；轴力量纲为kN,弯矩量纲为kN·m。

3.4 拱屈曲分析

由于该种结构体系目前使用较少，为了保证结构设计的安全性，在多曲拱设计时，按两种方式进行稳定承载力验算，一是按JGJ/T 249—2011《拱形钢结构技术规程》[5]中的无铰拱计算方法进行验算，二是通过线性屈曲分析确定拱的计算长度系数[6-7]，再按GB 50017—2017《钢结构设计标准》[8]进行验算。

根据内力分析可知，恒荷载、活荷载和温度为拱的主要控制荷载，其中“恒载+活载”是拱的基本承载模式，因此，采用“1.0×恒荷载+1.0×活荷载”的荷载组合进行线性屈曲分析，其中活荷载按多曲拱的全跨和半跨两种方式施加。图10为结构的前两阶屈曲模态，一、二阶模态主要表现为拱的面外和面内屈曲，对应的临界荷载系数分别为383.3、502.4。根据欧拉公式(1)反算拱的计算长度系数[6]。

图10 前两阶屈曲模态Fig.10 The first second-order buckling modals

μ=π(EI/Ncr)0.5/l

(1)

式中：EI为该构件发生屈曲方向的弹性抗弯刚度；Ncr为该构件的屈曲临界荷载，由线性屈曲分析得到；l为构件的几何长度。

经分析，拱面外、面内计算长度系数为1.29～1.38。在构件稳定验算时，拱的面内、面外计算长度系数均取为1.5。

3.5 构件应力比分析

图11为各杆件在包络工况下的应力比分布云图，大部分构件应力比在0.6以内。按两种验算方式得到多曲拱最大应力比为0.71，组合拱最大应力比为0.46，后排斜柱最大应力比为0.60，均满足设计要求。此外，在一层拱节点区域，应力比较大，但由于该处节点采用铸钢节点，具体应力比详节点分析部分。

a—构件应力比云图;b—构件应力比。图11 应力情况Fig.11 Stress of members

3.6 结构整体稳定分析

线性屈曲得到的稳定承载力仅为结构失稳的上限值，几何非线性对结构稳定承载力有显著影响，因此，需要对整体结构进行非线性稳定分析，同时考虑几何非线性，并考虑结构的初始几何缺陷[3-4]。初始缺陷的分布是随机的，采用“一致缺陷模态法”来近似模拟。将初始缺陷按结构最低阶屈曲模态分布，其最大初始缺陷取为拱跨度的1/300[7-8]。

由3.4节的线性屈曲分析可知，结构的前两阶屈曲模态均表现为拱的面内、面外屈曲，由此可见，拱的稳定性对结构的整体稳定至关重要。因此，选取拱变形最大的点作为位移法的控制点进行非线性分析。

图12a为拱位移控制点在“1.0×恒荷载+1.0×活荷载”作用下的荷载系数-位移曲线，其荷载系数随变形基本呈线性增长，荷载系数-位移曲线未出现拐点。当控制点水平位移达到350 mm，竖向位移达到450 mm时，多曲拱和后排斜柱开始屈服，此时多曲拱最大应力为359.4 MPa，斜柱最大应力为338.2 MPa(图12b)，对应荷载系数为17.43。综上可知，由于多曲拱的截面和壁厚均较大，承载力较高，在逐渐加载过程中，当截面达到屈服时，多曲拱未发生屈曲失稳，由此可见，结构稳定承载力不起控制作用。

a—荷载-位移曲线；b—控制点水平位移达349 mm应力分布，MPa。图12 位移情况Fig.12 Displacement

3.7 节点分析

一层平面布置图中GL2、GL3、GL4、弧形斜撑与多曲拱相连(图6a、c)，形成复杂空间节点，难以按常规框架节点进行设计，且该节点为关键节点，若节点破坏将导致结构的整体失稳或连续性倒塌，同时根据 “强节点弱构件”的设计要求[4]，节点承载力必须加强。为此，将该处节点设计成铸钢节点(图6c、图13)，要求节点极限承载力不小于荷载设计值的2.5倍，铸钢钢号根据《钢标》[8]选用ZG340-550H，铸钢制作满足相应规范要求。取节点中心至2倍杆件截面高度范围作为铸钢节点。由于加工制作要求，铸钢从汇交中心至铸钢节点杆件端部，由实心截面逐渐过渡到2倍原截面壁厚(图13)。

a—铸钢三维模型;b—铸钢杆件中心剖面,mm。图13 铸钢节点Fig.13 Cast steel joints

采用ABAQUS6.14-5对铸钢节点进行有限元分析，铸钢弹性模量Es=2.06×105MPa，泊松比0.3，单元类型为实体单元C3D10，材料本构关系采用理想弹塑性本构[9]。为了便于节点分析，同时使分析结果更偏于保守，节点边界条件按图14a进行设置，将节点两侧多曲拱进行固接，在剩余杆件端部施加包络工况下杆件内力。分析时采用静力分析步，并考虑几何非线性。

由于节点区应力复杂，采用von Mises 屈服准则判断节点是否失效。从Mises应力云图(图14b)可以看出，节点区大部分应力在100 MPa以内，只有小部分区域应力为161 MPa，最大应力比为0.61(161/265)，综上可以判断节点处于弹性状态。

a—模型边界条件;b—节点应力,MPa。图14 节点边界条件及Mises应力云Fig.14 Boundary conditions and Mises stress nephogram of joints

为得到对应杆件节点的极限抗弯承载力，在图14a的模型边界条件基础上，以在杆件1的端部施加竖向位移为例，得到杆件1 的弯矩-位移曲线(图15)，可以看出，极限抗弯承载力为Mju=40 096 kN·m，杆件1端部弯矩设计值为M=5 982 kN·m，两者比值为Mju/M=6.7，经验算，节点极限承载力满足设计要求。

图15 节点弯矩-位移曲线Fig.15 Relations between bending moment and displacement of joints

3.8 舒适度分析

由图7可知，结构前4阶振型均为竖向振型，第一、第二振型变形最大为一层拉拱梁悬挑区域，竖向自振频率分别为2.96,3.85 Hz；第三、四振型变形最大区域为屋面拱顶两侧，竖向自振频率分别为4.72,5.43 Hz。结构第一阶竖向自振频率略小于规范限值3.0 Hz[10]，第二、三、四阶竖向自振频率均满足规范要求，因此，基于第一阶竖向自振频率进行振动加速度响应分析。混凝土弹性模量放大1.35倍，阻尼比取0.04[10]，步行荷载曲线采用MIDAS Gen提供的IABSE曲线[11-12]。选取一层最不利位置计算楼盖的振动响应，共15个加载点，其中点A～F为竖向加速度提取点(图16a)。按单人慢走、单人快走、单人慢跑和单人快跑四种典型激励工况施加于楼盖[12-13]，各工况下的时程曲线见图16b～e。

a—一层加载位置;b—单人慢走;c—单人快走;d—单人慢跑;e—单人快跑。图16 加载位置及激励时程曲线Fig.16 Time history curves of exciting forces and its acting positions

在各激励工况下，提取点的竖向加速度时程曲线及最大竖向加速度分别见图17和表4，从中可以看出，最大竖向加速度为0.145 m/s2，小于规范[10]限值0.15 m/s2。综上，舒适度满足正常使用要求。

表4 不同激励下楼盖竖向振动加速度Table 4 Vibration acceleration of the floor system under different excitation actions m/s2

4 拱、斜柱与桩基础连接

图2为结构与典型地质剖面关系，地勘单位对工程建造区域及周边一定范围进行了勘察，未发现滑坡、崩塌、泥石流、地面塌陷、地下洞室、断层破碎带，亦未见有断层，场地现状连续稳定，地表水不发育，无地下水。

本工程基础均采用嵌岩桩基础，采用中风化砂岩作为持力层，在各种荷载组合下，拱脚、柱脚均未出现拉力，因此，各桩基础均按抗压桩进行包络设计。由于多曲拱拱脚位于斜坡，为了能设置基础，同时抵抗较大的拱脚推力，多曲拱采用斜桩基础，桩直径为2.1 m。为了使斜桩基础能有效传递拱脚反力，斜桩基础设计时采取了两项加强措施[14-15]：1)保证斜柱外侧岩石厚度不小于3.0 m，岩石厚度应从完整中风化基岩起算。为此，利用点云技术获取现场地形数据，再利用Smart 3D软件将地形数据处理成三维地形模型，最后利用Rhino软件将三维地形模型与结构模型合并，从而可以根据三维模型调整斜桩开挖的角度以保证斜柱外侧岩层厚度；2)保证斜桩埋置深度不小于6.5 m，埋置深度从强风化泥岩起算。对于后排斜柱，采用直桩，桩直径为1.3 m。