基于点云数据的网架结构提升变形智能监测方法*
2022-03-24金钦明程国忠李东声陈莎莎王瑞荣毕静刚
金钦明 程国忠 李东声 王 聪 陈莎莎 王瑞荣 毕静刚
(1.中建铁路投资建设集团有限公司,北京 102601;2.重庆大学土木工程学院,重庆 400045;3.深圳大学土木与交通工程学院,广东深圳 518060)
0 引 言
网架结构是多根杆件按照一定规律的网格形式并通过螺栓球或焊接球连接形成的高次超静定空间结构,它可充分发挥空间三维捷径传力的优势,满足日益复杂化、美观化的建筑外观设计需求。网架结构具有刚度大、质量轻、受力合理、稳定性高、施工周期短以及工业化程度高等优势,被广泛用作体育场馆、机场航站楼、博览会展厅和高铁站房等大型民用基础设施的屋盖[1]。网架结构的常用施工方法包括:高空散装法、分块吊装法、整体吊装法以及整体提升法等[2]。其中,高空散装法、分块吊装法和整体吊装法存在高空作业多、施工效率低、施工安全性难以保障等限制[3],常用于小型网架结构的施工。对于大型网架结构而言,应用最广泛的施工方法是整体提升法。整体提升法是指在设计位置就地完成网架结构拼接后,采用液压同步提升技术对网架结构进行整体提升[4]。对于整体提升法而言,影响施工质量和安装精度的关键因素之一是网架结构提升的变形量。目前,网架结构提升变形监测手段主要包括全站仪、光电测距仪等,这些设备只能对局部点进行监测,无法对网架提升变形进行全覆盖的监测[5-6]。因此,目前亟需一种全面且高效的变形监测方法。
目前,三维激光扫描技术因测量精度高、扫描效率高、受外界影响小、可操作性强等优点而受到建筑业研究人员的青睐。三维激光扫描仪(图1)通过主动发射激光束的方式来完成对目标点的测量,可以快速获得扫描环境内的全景三维点云数据,具有数据精度高、受外界影响小、可操作性强等优点。三维激光扫描仪应用于施工变形检测的最大优势是可以全覆盖地获得结构变形,提供更加全面、充分的变形信息。为了改善建筑业的传统监测方法和提高监测智能化程度,学者们开展了基于三维激光扫描仪的施工进度智能监测,但研究对象主要集中于刚性的建筑构部件[7-8]。提升前与提升后的网架结构处于不同受力状态,存在不同程度的变形。基于三维激光扫描技术的结构变形智能监测需要将结构变形前后的点云数据进行配准[6]。目前点云数据的非刚性配准通常需要人为选择配准点,存在人为主观误差。因此,目前相关研究方法不适用于对网架结构提升变形进行智能监测。

图1 三维激光扫描技术Fig.1 3D laser scanning technology
为此,以泸州高铁站为工程背景,开展基于点云数据的网架结构提升变形智能监测研究,包括点云数据预处理、点云数据非刚性配准、提升变形可视化3个方面。针对提升前与提升后网架结构点云数据的非刚性配准,提出了集球心智能定位、球心粗匹配、球心非刚性配准于一体的综合算法。研究成果以期为网架结构提升变形监测提供理论和算法基础支撑。
1 工程概况
泸州高铁站(图2)位于四川省泸州市马潭区境内,总建筑面积3.999 8万m2,建筑高度40.2 m。泸州高铁站主要包括侧式站房和高架站房两部分,高铁站屋盖均采用大跨网架结构,侧式站房屋盖最大跨度为81 m,高架站房屋盖最大跨度为54 m。大跨网架结构中,圆杆均通过焊接球进行连接(图3),圆杆最大直径为450 mm,焊接球最大直径为800 mm。
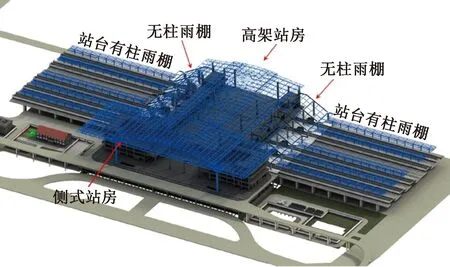
图2 泸州高铁站结构示意Fig.2 A schematic digram for the structure of Luzhou High-Speed Railway Station

图3 典型节点Fig.3 Typical joint
高架站房需进行3次提升:第1次是将网架结构从标高9.45 m提升到标高16.90 m,提升结构质量为967 t;第2次是将网架结构从标高16.90 m提升到标高22.45 m,提升结构质量为1 228 t;第3次是将网架结构从标高22.45 m提升到标高27.50 m,提升结构质量1 276 t。第3次提升时,网架结构共设置20个吊点,吊点的布置见图4。以高架站房屋盖的第3次提升变形监测为例,对基于点云数据的网架结构提升变形智能监测方法进行介绍(图5)。
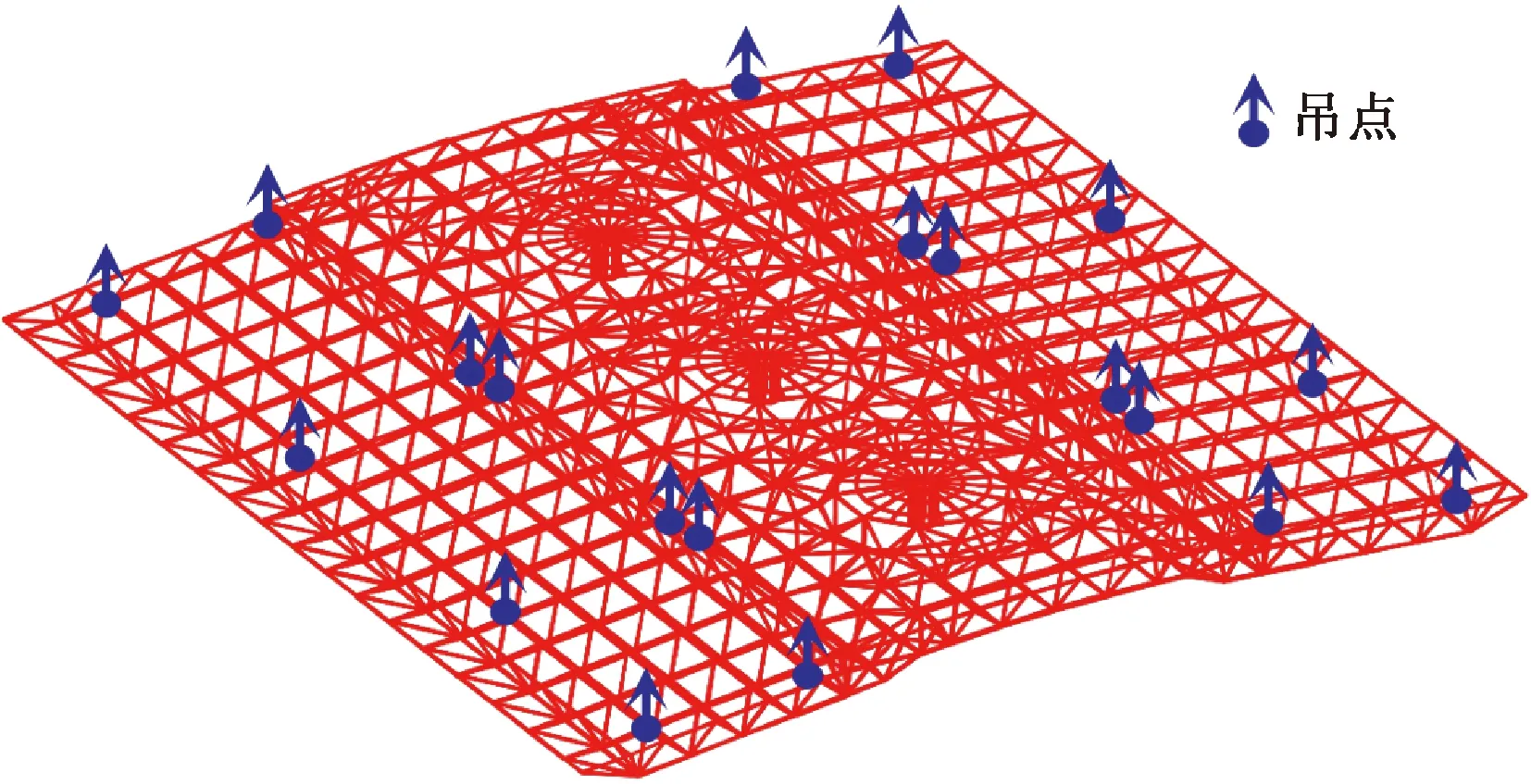
图4 吊点布置Fig.4 Arrangements of lifting points

图5 网架结构提升变形智能监测技术流程Fig.5 A technical flowchart of intelligent deformation monitoring for lifting space frames
2 点云数据预处理
为实现网架结构的全覆盖扫描,选用最大量程为150 m的Faro S150三维激光扫描仪对提升前与提升后的网架结构分别进行多站点扫描(图6)。基于重叠区域的焊接球球心,利用点云处理软件对扫描点云数据进行粗拼接,继而采用迭代最近邻算法对扫描点云数据进行精细化拼接。拼接后的点云数据中包含防护网、混凝土构部件等大量背景噪声数据,这会显著地增加点云数据处理的难度。为此,拼接后的点云数据须要进行人工去噪。采用基于图结构滤波算法[9]对去噪后的网架结构点云数据进行轻量化(图7),轻量化后的点云数据见图8。

图6 数据采集Fig.6 Data acquisition

a—原始点云数据;b—10%采样的点云数据。图7 点云数据轻量化Fig.7 Light-weight point cloud data
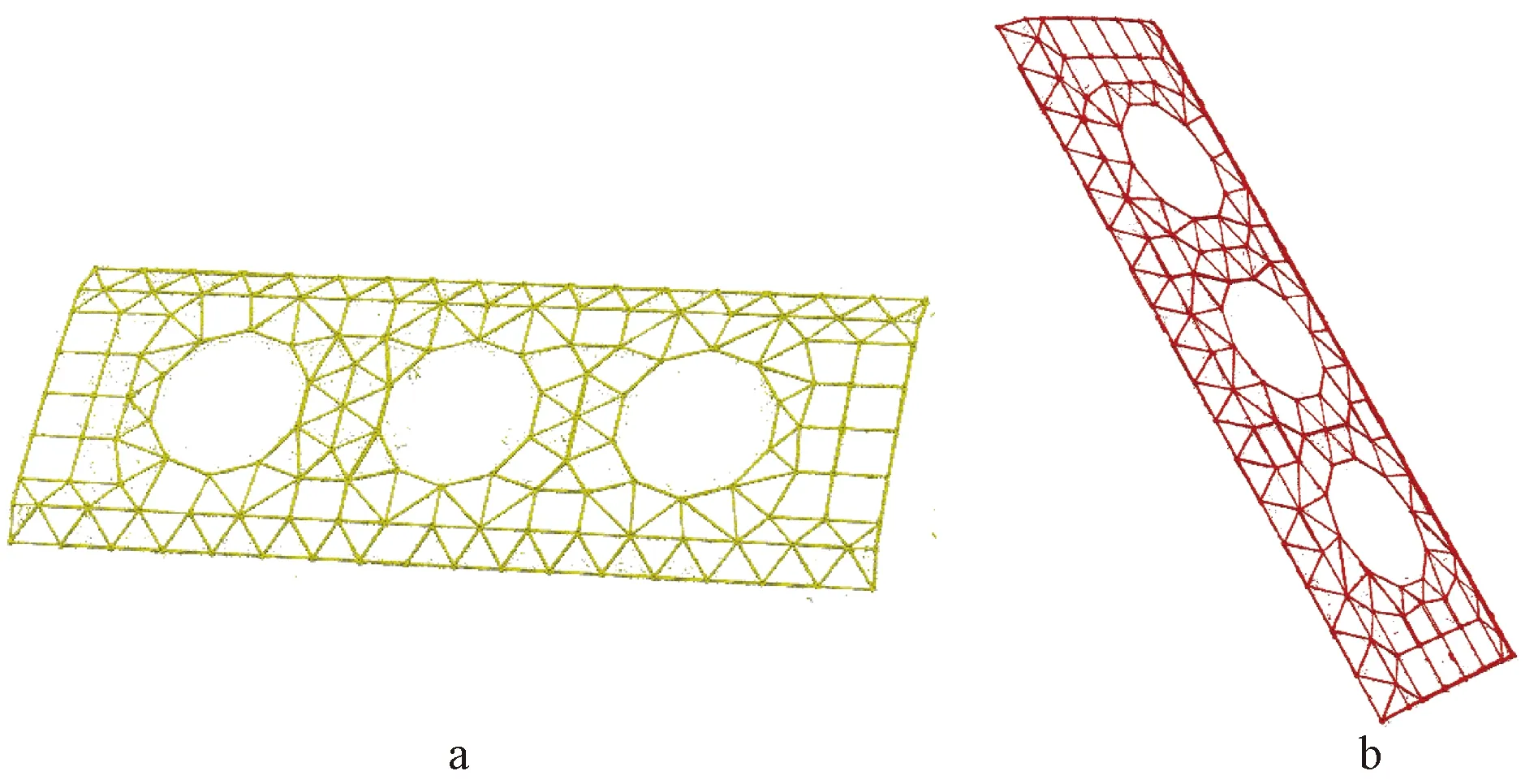
a—提升前;b—提升后。图8 网架结构的部分点云数据Fig.8 Partial point cloud data of space frames
3 点云数据非刚性配准
非刚性配准问题通常指具有一定差异的两个目标对象通过某个仿射变换实现最优匹配[10]。考虑到完整点云数据的非刚性配准难度大、效率低,提出采用焊接球球心代替完整点云数据进行网架结构变形监测的策略。网架结构点云数据的非刚性配准具体包括球心智能定位、球心粗匹配以及球心非刚性配准。
3.1 球心智能定位
焊接球球心智能定位包括球点云数据智能识别、球点云数据智能分割以及球拟合。
3.1.1球点云数据智能识别
去噪后的点云数据由杆件点云数据与焊接球点云数据组成。考虑到杆件和焊接球点云数据的曲率特征、线性特征、发散性特征等局部邻域特征存在明显差异,因此可以通过逐点计算局部邻域特征对球点云数据进行智能识别。
由于网架结构的点云数据量大且点云数据无拓扑关系,为提高球特征检测效率,需对点云数据建立多维二叉树(KD树)结构[11]。对于任意计算数据点pi,采用基于范围搜索的k最近邻算法[12]。可得到pi的局部邻域点集合Ωi={pj|‖pi-pj‖≤dt},其中dt表示预设的邻域距离阈值。Ωi可由矩阵Pi=[pi,1,pi,2,…,pi,n]进行表示,其中n为pi的局部邻域点数量,pi的协方差矩阵Σi通过下式进行计算:
(1)

对Σi采用特征值分解可得矩阵特征值(λ1≥λ2≥λ3>0)。线性特征Lλ与发散性特征Sλ可按下式进行计算[13]:
(2)
(3)
邻域距离阈值和特征筛选阈值是影响球点云数据智能识别的关键参数。经多次测试,计算Lλ和Sλ的邻域距离阈值分别取0.4,0.6 m,同时选取Lλ<0.6和Sλ>0.15作为球点云数据识别准则,可实现球点云数据智能识别。图9为球点云数据智能识别的结果,其中红色数据点为球点云数据,黄色数据点为非球点云数据。

图9 球点云数据智能识别Fig.9 Intelligent identification of point cloud for welded spherical joints
3.1.2球点云数据智能分割
采用聚类算法(DBSCAN)[14]对识别出的球点云数据进行智能分割,从而得到每个球对应的点云数据。球点云数据智能分割时,选取任意点为种子点,以固定搜索半径进行点云数据扩充,直到固定搜索半径无点云数据为止,从而得到一个球的点云数据。根据DBSCAN聚类算法原理可知,固定搜索半径是智能分割的关键参数,高架站房屋盖的杆件长度均超过1 m,故固定搜索半径可取0.6 m。球节点云数据智能分割效果见图10。

图10 球节点云数据智能分割Fig.10 Intelligent data segmentation of point cloud for welded spherical joints
3.1.3球拟合
采用算法(RANSAC)[15]对分割后的球点云数据进行球拟合。球拟合时,首先从分割后的球点云数据中随机选取ms个点;然后根据选取的ms个点计算球心坐标和球半径;接着对拟合的球进行评价,评价函数C按下式计算:
(4)

式中:ei为第i个点到球面的欧式距离;t为球面点的允许误差。
重复上述过程In次,最后输出评价函数最大对应的球心坐标和球半径。对于RANSAC算法而言,最关键的3个控制参数为In、ms以及t,In可根据蒙特卡洛法进行计算:
(5)
式中:ε为球面点的百分比,设置为50%;η0为球拟合正确的概率,设置为0.99。
ms设置为4,t设置为0.01 m。球拟合结果见图11。

图11 球节点数据拟合Fig.11 Numerical fitting of spherical joints
3.2 球心粗匹配
提升后的大跨度网架结构通常会发生较大的整体变形且网架结构存在大量的局部四点全等集,因此采用基于欧式距离的四点全等集(4PCS)算法[16]难以实现球心匹配。网架结构提升前后相邻焊接球之间的欧式距离存在较小的差异,故可采用图结构特征作为节点球心匹配的依据。
3.2.1图结构特征计算
首先,对球心集建立KD树结构;然后,采用k最近邻算法确定每个球心的邻近图[17]:
(6)
式中:vi和vj分别为第i个和第j个节点球心;aij和aji均为球心i与节点球心j的邻近关系系数,aij取0或1,0表示节点球心i与节点球心j不存在邻近关系,1表示球心i与球心j存在邻近关系;KNN(·)表示k最近邻筛选,k取4。
最后,通过邻近关系系数可得到任意球心i的集聚系数Ci[18-19]:
(7)
图12分别展示了提升前后的球心集聚系数。
3.2.2图结构特征匹配
对3.2.1节得到的球心集聚系数进行统计,可得到球心集聚系数的分布图(图13、14)。可以看出:提升前后球心集聚系数的分布基本一致,这为图结构特征匹配提供了良好的理论依据。首先,从提升前的球心集中选取低频球心集聚系数(Cd)对应的球心集P;然后,从提升后的节点球心集中选取集聚系数为Cd的球心集Q;接着,对球心集P和Q进行全排列,生成候选的球心匹配对(P-Q);最后,对候选的球心匹配对进行评价,选出最优的球心匹配对。

图13 提升前的球心集聚系数分布Fig.13 Distribution for clustering coefficients of spherical joint conters before lifting
候选的节点球心匹配进行评价时,对每一个候选的球心匹配对按下式求得旋转矩阵R与平动矩阵T:
(8)
式中:pi和qi分别是P-Q中提升前与提升后的球心坐标;μp和μq分别是P-Q中提升前与提升后球心坐标的均值;n为P-Q包含球心匹配对的数量;W为协方差矩阵;对角矩阵Σ、左奇异向量U以及右奇异向量V均由矩阵W奇异值分解得到。
W=UΣVT
(9)
R=UVT
(10)
T=μq-Rμp
(11)
最优变换矩阵Ropt与Topt通过下式确定:
(12)
式中:m为球的总数量;Xi和Yi分别为提升前和提升后的球心坐标,对应关系通过最近邻算法确定。
最优变换矩阵Ropt与Topt对应的球心匹配对即为最优的球心匹配对,基于图结构特征的球心最优匹配见图15。基于图结构特征的球心匹配确定了提升前后球心的对应关系,为球心非刚性配准提供了良好的初始解。

图14 提升后的球心集聚系数分布Fig.14 Distribution for clustering coefficients of spherical joint centers before lifting

图15 基于图结构特征的球心最优匹配Fig.15 Optimal matching for spherical joint centers based on graph features
3.3 球心非刚性配准
由于网架结构的提升变形通常为低阶模态,提升前后的网架结构存在大量相同局部特征。然而,现有的非刚性配准算法是建立在目标对象变形前后存在少量相同局部特征且重叠区域不规则的基础上。为此,亟须提出一种面向网架结构提升变形智能监测的非刚性配准算法。
低阶变形具有同号性质(图16)。因此,球心非刚性配准问题可以表述为:

图16 低阶变形的同号性Fig.16 Homogeneity in low-order deformation
(13)
s.t.[RXi+T-Yi]z≥0i∈[1,m]
(14)
式中:[·]z表示提升变形在Z轴上的分量。
为了高效、快速地求解式(13),基于贪心策略和局部正交普氏算法提出球心非刚性配准算法(表1)。算法具体步骤为:1)基于粗匹配后的球心坐标,计算负变形球心的占比θ;2)选出所有负变形球心对,组成集合{Xn-Yn};3)采用正交普氏算法对集合{Xn-Yn}进行匹配,从而获得变换矩阵R与T;4)基于变换矩阵R与T,对提升后的球心进行临时变换;5)基于临时变换后的球心,重新计算负变形球心占比θ;6)若θ值变小,基于变换矩阵R与T对提升后球心进行正式变换,并重复步骤3)~5);7)若θ值未变小,基于贪心策略从集合{Xn-Yn}提出负变形最大的球心对,并重复3)~5),直至集合{Xn-Yn}的元素小于3。

表1 球心非刚性配准算法Table 1 The non-rigid matching algorithm for spherical joint centers
从图17可以看出:负变形球心占比θ随着迭代次数迅速降低,表明提出的球心非刚性配准算法具有良好的收敛性。球心非刚性配准的结果见图18。

图17 球心非刚性配准算法收敛结果Fig.17 Convergence results of the non-rigid matching algorithm of spherical joint centers
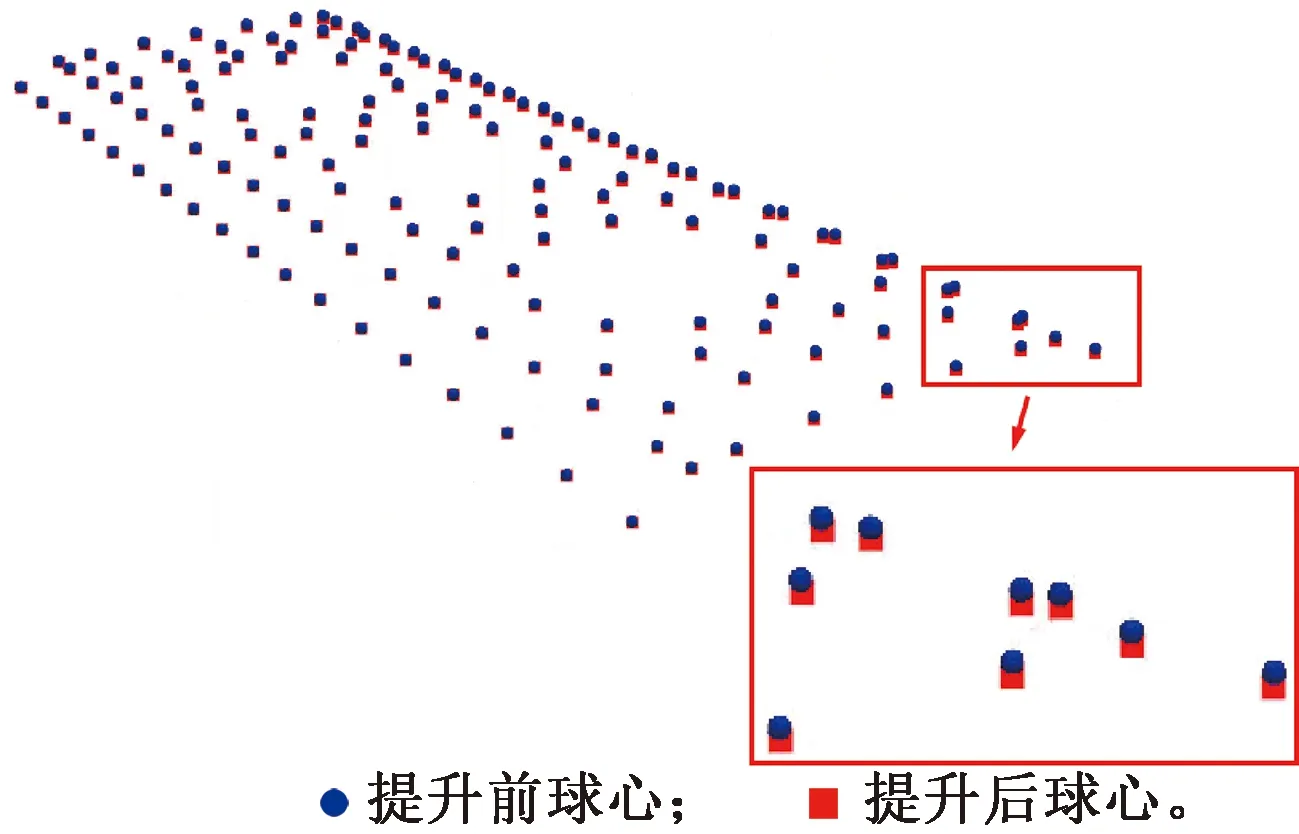
图18 球心非刚性配准结果Fig.18 Non-rigid matching results of spherical joint centers
4 提升变形可视化
点云数据非刚性配准后,采用最近邻算法计算每个焊接球球心的偏移距离,偏移距离的偏差以彩色编码差异图进行显示。图19为高架站房屋盖第三次提升变形的彩色编码差异图。从图中可以看出,高架站房屋盖最大提升变形位于网架结构的端部,变形量为0.396 m。
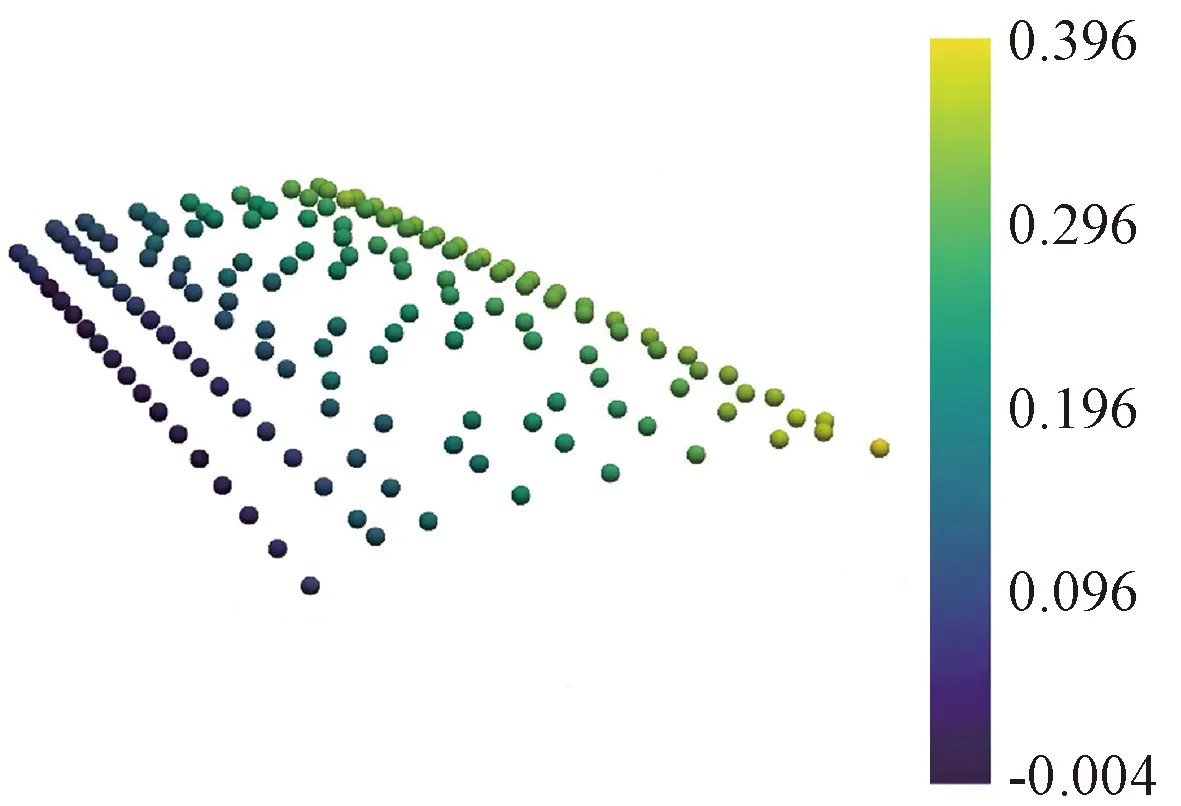
图19 网架提升变形监测结果 mFig.19 Deformation monitoring results of the space frame during lifting
5 结束语
以泸州高铁站为工程背景,开展了基于点云数据的网架结构变形智能监测研究,主要研究结论如下:
1)提出了基于点云数据的网架结构变形智能监测方法,集成应用了聚类算法、随机抽样一致性算法、图结构方法、球心非刚性配准算法,最终形成了网架结构变形智能监测综合算法。
2)提出采用焊接球球心代替完整点云数据进行网架结构变形监测的策略,大大降低了变形监测的难度,实现了高效、快速的点云数据非刚性配准。
3)提出了集球心智能定位、球心粗匹配、球心非刚性配准于一体的网架结构点云数据非刚性配准算法。
4)高架站房屋盖最大提升变形位于网架结构的端部,变形量为0.396 m。
