高三一轮复习检测题(必修1、必修2、选修3-5)B卷参考答案与提示

1.C 提示:对绳子进行分析可知,两队队员对绳子的拉力是一对平衡力,大小相等,方向相反,选项A 错误。对两队队员组成的整体进行分析可知,当整体突然向获胜一方移动时,获胜一方受到的静摩擦力大于另一方受到的静摩擦力,选项B 错误。双方相持时,对其中一个运动员进行受力分析,在竖直方向上有N=mg,即支持力N不变,因此运动员改变身体与地面之间的夹角时,运动员受到地面的弹力不会变,选项D 错误;在水平方向上有T=f,当绳子拉力T增大时,静摩擦力f增大,静摩擦力和支持力的合力增大,即地面对运动员的作用力增大,选项C正确。

2.C 提示:根据位移与速度的关系式得v0=2ax,其中v0=30 m/s,x=75 m,解得a=6 m/s2,选项A 错误。又有a=μg,解得μ=0.6,选项B 错误。根据速度公式v=v0-at可得,t=3 s时刻,汽车的速率v3=12 m/s,选项C 正确。汽车减速到零所用的时间,因此0～6 s内,汽车的位移等于75 m,选项D 错误。

3.D 提示:如图1所示,设每个爪与锅之间的弹力为N,其方向与竖直方向之间的夹角为θ,正对的两爪之间的距离为d,根据几何关系得根据平衡条件得4Ncosθ=mg,解得N=因此R越大,sin θ 越小,cosθ越大,N越小。

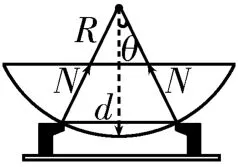
图1

4.A 提示:女运动员做圆锥摆运动,对女运动员进行受力分析,她受到重力mg和男运动员对她的拉力F,如图2所示。女运动员在竖直方向上受到的合力为零,即Fsin 45°=mg,解得F=,选项C 错误。女运动员在水平方向上受到的合力提供其做匀速圆周运动所需的向心力,即Fcos 45°=ma向,解得a向=10 m/s2,选项A 正确;根据a向=ω2r,r约为1 m 可知,女运动员的角速度约为3.14 rad/s,选项B 错误。对男运动员进行受力分析得N=Fcos 45°+Mg=450 N+Mg,选项D 错误。

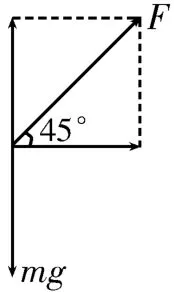
图2

5.B 提示:动车速度达到最大时,牵引力与阻力平衡,则行驶过程中动车受到的阻力大小,选项A 错误。当动车的速度为时,动车的牵引力,根据牛顿第二定律得F-f=ma,解得a=,选项B 正确。从启动到速度增大为vmax的过程中,动车牵引力所做的功等于动车动能增加量和克服阻力做功之和,故大于,选项C错误。因为动车不是做匀变速直线运动,所以在只知道最大瞬时速率的情况下,无法估算平均速率,也无法得出路程,选项D 错误。

6.B 提示:设星球表面的重力加速度为g,风帆与滑块的总质量为m。沿斜面方向,根据牛顿第二定律得mgsin θ-μmg cosθkv=ma,解得则a-v图像的斜率,即风帆与滑块的总质量,选项A 错误。设星球的第一宇宙速度为v,则当滑块的速度为零时有mgsin θ-μmg cosθ=ma0,解得g=v=,选项B正确。在星球表面,万有引力等于重力,即,星球体积,星球密度,解得ρ=,选项C 错误。根据,解得星球近地卫星的周期,选项D 错误。

7.BC 提示:水流垂直落在与水平面成30°角的水轮叶面上,水平分速度和竖直分速度满足,解得,选项A错误,B 正确。水流冲击水轮叶面瞬间的速率,根据v=ωR,解得,选项C正确,D 错误。

9.AB 提示:根据v-t图像可知,货物先向上做匀加速运动,再向上做匀速运动,因此传送带匀速转动的速度大小v=1 m/s,选项A 正确。0～0.4 s 货物的加速度a==2.5 m/s2,根据牛顿第二定律得μmgcos θ-mg sinθ=ma,解得选项B正确。根据v-t图像可知,A、B两点之间的距离对应图像与横坐标围成的面积,即s=×(16+15.6)×1 m=15.8 m,选项C错误。根据动能定理得Wf-mgssinθ=,解得Wf=795 J,选项D 错误。

10.AD 提示:轻绳被拉断瞬间,弹簧的弹力等于kx,对长木板应用牛顿第二定律得kx=Ma,解得a=,选项A 正确。轻绳被拉断之前对由长木板和滑块组成的系统有拉力作用,因此系统的动量不守恒,选项B 错误。弹簧恢复原长时长木板有动能,因此滑块的动能小于,选项C 错误。设轻绳被拉断时滑块的速度为v1,弹簧弹力做功,根据动能定理得,设轻绳被拉断后长木板和滑块最终以速度v2向左运动,根据动量守恒定律得mv1=(M+m)v2,根据功能关系得,解得μ=,选项D 正确。

11.(1)9.4 (2)滑轮的轴不光滑(或滑轮有质量,软绳有质量,物体在运动过程中受到空气阻力,手机在下落过程中发生摆动等)

提示:(1)根据a-t图像读出手机的加速度a=4.7 m/s2,根据牛顿第二定律得(mBmA)g1=(mA+mB)a,解得g1=9.4 m/s2。

提示:(1)游标卡尺的读数d=5 mm+2×0.1 mm=5.2 mm。(2)滑块通过光电门Ⅰ的瞬时速度v1==0.20 m/s。(3)滑块在沿光滑的斜面下滑的过程中机械能守恒,则,整理得h1-h2=

13.(1)物体恰好能通过D点,根据牛顿第二定律得mg=,解得vD=2 m/s。(2)物体经过B点时的受力情况如图3所示,根据动能定理可知,物体由B点运动到D点的过程中有,根据牛顿第二定律得,解得vB=m/s,N=60 N。(3)物体在水平面上做匀加速直线运动,根据牛顿第二定律得F-μmg=ma,根据位移与速度的关系式得2ax=v2B,解得x=2 m。

图3

14.(1)运动员从A点滑到O点,根据机械能守恒定律得mgh=,解得v=(2)运动员从离开O点到落在斜坡上,根据平抛运动规律得,解得(3)运动员从离开O点到落在斜坡上,根据动量定理得Δp=mgt,解得,方向竖直向下。

16.(1)t=0时刻,物体P和Q之间发生弹性碰撞,设碰撞后物体P的速度是v1,物体Q的速度是v2,根据动量守恒定律和能量守恒定律得,解得v1=6 m/s,v2=-3 m/s。物体P与Q发生碰撞后,物体P向右运动,设物体P的加速度大小为a1,根据牛顿第二定律得μ1Mg=Ma1,解得a1=1 m/s。①设经过时间t1,物体P向右运动通过B点,根据运动学规律得L=v1t1-,解得t1=(6-) s=0.7 s或t1==11.3 s(不符合实际,舍去)。因为t1＜2 s,所以物体P向右通过B点时,不会被探测到。②设经过时间t2,物体P与挡板碰撞后向左运动通过B点,根据运动学规律得,解得t2=(6-) s=2.54 s或t2=(6+) s=9.46 s(不符合实际,舍去)。因为2 s＜t2＜4 s,所以物体P向左运动通过B点时,会被探测到。(2)物体P与Q发生碰撞后,物体Q向左运动,设物体Q的加速度大小为a2,根据牛顿第二定律得μ2mg=ma2,解得a2=3 m/s2。物体Q向左运动的时间t==1 s,物体Q从A点开始向左运动的距离x==1.5 m,物体P从发生第一次碰撞到停止运动通过的路程s==18 m。因为s-4L＞x,所以物体P与Q能发生第二次碰撞。物体Q向左运动的时间t=1 s,在第一次碰撞结束后1 s 内,物体P通过的路程s1=v1t-=5.5 m,s1＜4L+x,因此物体P与Q的第二次碰撞发生在物体Q静止之后,即在第二次碰撞之前,物体P通过的路程为4L+x,物体Q通过的路程为x。从第一次碰撞到第二次碰撞的过程中,系统产生的内能E=μ1Mg(4L+x)+μ2mgx,解得E=39.5 J。