基于纯方位的无人机遂行编队飞行中的无源定位问题
2022-03-24周心雯
周心雯
(广西师范大学,广西 桂林 530000)
1 预备知识和问题描述
无人机技术发展迅猛,广泛应用于民用和军用领域,在军用的目标追踪方面,为了保证无人机的隐蔽性,尽可能避免外界干扰,无源定位跟踪系统逐渐成为研究热点。纯方位跟踪系统是对目标进行连续观测,积累测角信息,从而获得目标状态的精确估计[1],受成本和质量的限制,无源纯方位传感器被广泛应用于被动跟踪中的无源定位问题。根据测量方式的不同,无源定位的方式可以分为到达角度(Angle Of Arrival, AOA)技术、到达时间(Time Of Arrival, TOA)技术、到达频率差(Frequency Difference of Arrival, FDOA)技术以及到达时间差(Time Difference of Arrival, TDOA)技术[2-3]。不同无源定位的优、缺点见表1。

表1 不同无源定位方法的优、缺点
基于TDOA的无源定位具有便于观测、易获得信息以及易组网的优点,因此适用于无人机集群作战场景。利用TDOA对目标进行定位主要分为TDOA估计、TDOA结算以及目标定位3个步骤。因此,该文基于TDOA(到达时间差)定位法,利用目标到达接收站的时间差完成定位任务。
该文主要研究圆形阵列无人机队伍无源定位问题。首先,选择圆形阵列,以圆心为主发射器,其他作为辅助发射器,辅助发射器接收目标辐射的信号并转发至主发射器,主发射器同时接收辅助发射器和目标辐射的信号,测量信号从辅助发射器到达主发射器与信号从目标辐射到达主发射器的时间差[1],从测量与目标的物理关系出发,当发射信号的无人机位置无偏差且编号已知时,建立被动接收信号的无人机测角定位方程。其次,在已知目标接收到2个固定编号的无人机发射的信号的基础上,通过上述测角定位模型比较不同数量无人机在保持最优定位几何结构情况下的定位精度。根据接收的方向信息选择加权最小二乘迭代对观测方程进行求解,构建定位精度高、结构形式简单的协同定位模型,调整无人机的位置,给出协同定位目标的约束条件并介绍设计方案。最后,根据时差无源定位系统的误差几何稀释度,考虑纯方位无源定位情形,重点分析几何因子对目标定位的影响,得出无人机调整编队的队形方案[4]。
2 模型假设
模型假设如下:1) 假设无人机能正常发射和接收信号。2) 无人机信号传播速度恒定。3) 忽略多个无人机在群队之间的斥力和引力。4) 假设无人机不受内部噪声、传感器更新延迟、数据处理时延、通信局域性以及一般环境噪声等情况的影响[5]。
3 算法设计
该文只需要考虑当编队运动时均保持在空中的某一高度上,假设在圆形阵列中,发射信号的无人机对被动接收信号的无人机目标定位和跟踪问题。假定编队中各无人机保持恒定高度飞行,圆心的无人机与编队中任意2架无人机位置无偏差,将其余任意1架无人机作为目标被动接收信号,此定位为无源定位,接收信号的无人机与发射信号的无人机位置不同,在无卡曼尔滤波的影响下,考虑距离差,发射信号的无人机信号到达目标无人机的时间不同,根据TDOA定位方法,目标无人机只需要测量与信号到达的时间差就可以计算目标在空间中的位置。
选定一被动接收信号的无人机为目标,位于圆心的无人机(FYOO)为主发射信号器,编队中另外2架无人机(用符号表示)辅助发射信号,则信号到达被动接收信号的目标无人机的时间差如公式(1)所示。
式中:c为光速;r0为主发射器到目标无人机的距离;ri为辅助发射器到目标的距离;di为主发射器到辅助发射器的连线长度,di是已知常数。
假设ΔRi为各目标无人机到达主发射器与到达辅助发射信号无人机距离差,根据其物理关系可以得到公式(2)。
将公式(2)代入公式(1)并简化,如公式(3)所示。
简化后的方程仅包括均匀分布的圆形无人机编队的距离关系,因此,该问题可以根据TDOA定位法的内涵,利用研究距离差代替研究时间差,以此简化研究参数,忽略信号接收不稳定和数据处理时间等误差。当无人机编队在某一高度时,在X-Y的二维平面设目标相对于发射信号的无人机在x方向上的速度为vi,距离为ri,Y方向为li,则多发射器单目标时差定位系统的运动方程如公式(4)所示。
在该二维平面内,时差定位系统由3个发射信号的无人机以及1个被动接收信号的无人机构成,其中O为主发射器,C为辅助发射器,A、B为被动接收信号的无人机。如图 1所示。

图1 TDOA时差定位系统示意图
根据公式(4)所示的时差无源定位原理[5]可知,运动方程公式(3)可以代入公式(4),如公式(5)所示。
式中:(xi,yi)为X-Y的二维平面上初始位置有偏差的无人机位置坐标。
在时差定位系统中,2个辅助发射器以及被动接收信号的目标无人机与圆心主发射器的无人机的坐标关系如公式(6)所示。
式中:(xn,y0)为圆心主发射器无人机的坐标;(x,y)为被动接收信号的目标无人机的坐标。
将公式(6)代入公式(5),整理得到简化的定位系统位置关系,如公式(7)所示。
求解上述二元一次方程组就可以得定位系统各无人机坐标以及角度之间的关系,如公式(8)~公式(10)所示。
式中:μ(u,v)为任意坐标(u,v)的相角,μ∈[-π,π)。
联立公式(8)和公式(9)得到公式(11)~公式(13)。
综上所述,在模型假设的基础上,根据无人机选取的任意性,可确定单目标定位系统在圆形无人机编队中的通用运动模型。
在圆形矩阵的无人机编队中,以圆心的FY00无人机为主发射器,从其余9架无人机选择任意2架为辅助发射信号无人机,已知TDOA定位模型中的时间差是利用圆心无人机发射信号与其余辅助无人机发射信号到达目标无人机的时间差,除了以圆心的FY00无人机为主发射器、选取FY01的无人机为辅助发射信号之一外,在圆形矩阵中,现将X=[xtyt]T设为被动接收信号的目标无人机的位置,坐标圆心无人机的二维坐标是F0=[x0y0],其余2个辅助发射器的二维坐标为F1=[x1y1]和F2=[x2y2]。设主发射器无人机到接收信号的目标无人机的距离为r0,其余2个辅助发射器到接收信号的目标无人机的距离分别表示为ri,i=1,2。
发射信号的无人机与接收信号的目标无人机距离的数学关系如公式(14)~公式(16)所示。
发射信号的无人机i与主无人机发射信号的实际时间差如公式(17)所示。
将公式(14)、公式(15)代入公式(16),可以得到各坐标关系等式,如公式(18)所示。
公式(18)可以列出2个,将其写成矩阵形式,如公式(19)所示。
式中:A、X和B为矩阵。
问题转化为求关于X的非其次线性方程组的解,求接收信号无人机的位置可以转化为求矩阵X的解,在二维平面中矩阵X包括xT和yT的解,要想获得xT和yT的唯一解,就需要在矩阵A中A的秩为满秩(rank(A)=2),而A的秩为满秩的充要条件是A的行列式不为0,但是在圆形阵列中,i的任意性会导致(x0-xi)和(y0-yi)成比例,即A的行列式中某2行会成比例导致行列式的值为0,因此在已知以圆心的FY00无人机为主发射器、FY01的无人机为辅助发射信号之一的情况下,至少需要再添加1架辅助发射信号的无人机才可求解出xT、yT,又由公式(8)可知,当X1cosθ+Y1cosθ+ΔR1=0或=X2cosθ+Y2cosθ+ΔR2=0时,目标不可被观测[4]。如图 1所示,当θ=0的时候,如公式(20)所示。
因此,当θ角度满足以上公式时,有X1cosθ+Y1cosθ+ΔR1=0,那么这时目标难以接收信号产生信号差。
在已知以圆心的FY00无人机为主发射器、FY01的无人机为辅助发射信号之一的情况下,至少需要再添加1架辅助发射信号的无人机,且任意2发射信号的无人机连线及其延长线不含有接收信号的目标无人机,这样才可以对接收信号的目标无人机进行有效定位。
根据题目中无人机编队要求,需要把初始位置略有偏差的9架无人机经过多次调整到以FY00为圆心半径为100米的圆周上。对建立的单目标信号接收定位模型来说,通过2步加权最小二乘法求解被动接收信号的目标无人机位置的非线性方程组,即Chan算法,以此确定每一次调整时任意单目标的位置,对结果进行拟合就可以得出整体的调整方案。
首先,由题目附件所给的9架无人机的初始位置和坐标分别求出每架无人机与处于圆心无人机的距离差和角度差,将距离差和角度差放于直角二维坐标系中,得到点(xi,yi),如图2所示。
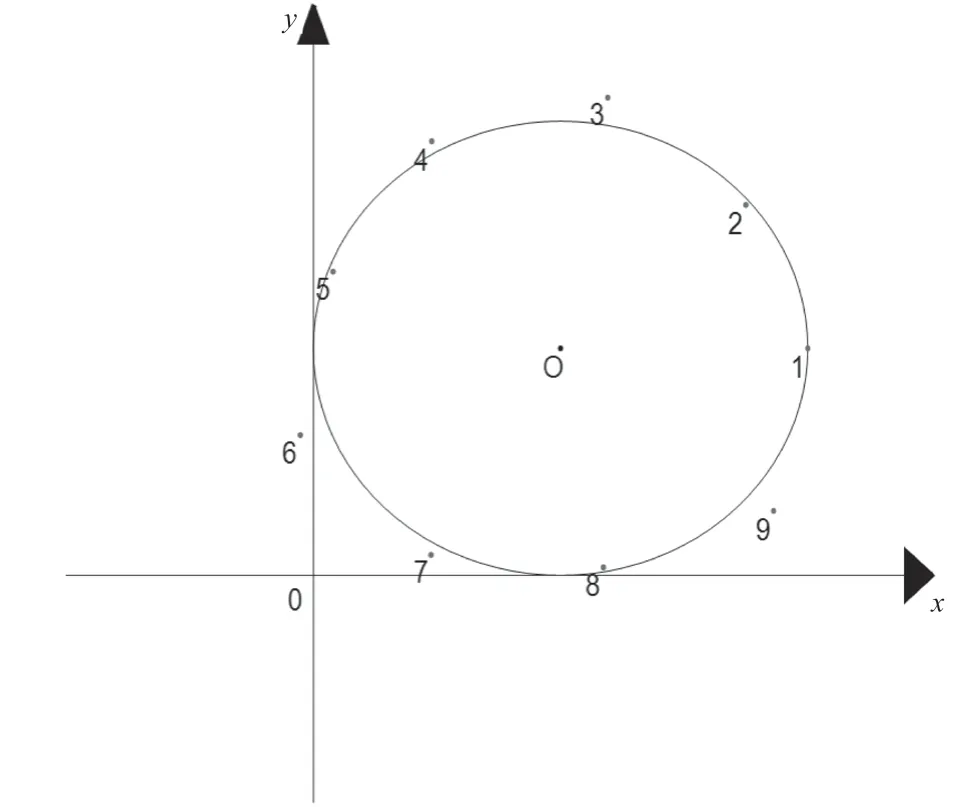
图2 无人机位置拟合直线图
这些点大致分布在一条直线附近,如图3所示。

图3 无人机的初始位置图
可用1个直线方程反应x与y之间的对应关系,现要确定该条直线方程,使这9个点的偏差平方和最小(最小二乘方),假设所求直线如公式(21)所示。
所测得到的9架无人机的偏差点为(Δxi,Δyi)。现要确定直线中未知参数a、b,以满足公式(22)。
使f(ab)为最小函数值,因此有公式(23)。
对这组关于a、b的线性方程进行整理,得到公式(24)。
求解公式(24),即得到f(a,b)的稳定点,如公式(25)、公式(26)所示。
为了进一步确定该点是极小值点,经过计算得公式(27)~公式(30)。
式中:faa为f对a的二阶导;fbb为f对a再对b的导;fbb为f对b的二阶导。
f(a,b)在取得最小值,那么就有公式(31)。
公式(31)为拟合后的圆周表达式。
调整初始位置有偏差的无人机,使其均匀分布在拟合圆周上,用(xj',yj')来表示需要移动到的均匀分布在圆周上的位置,同时考虑距离和角度偏移调整方案(如图 4所示),文字说明如下。
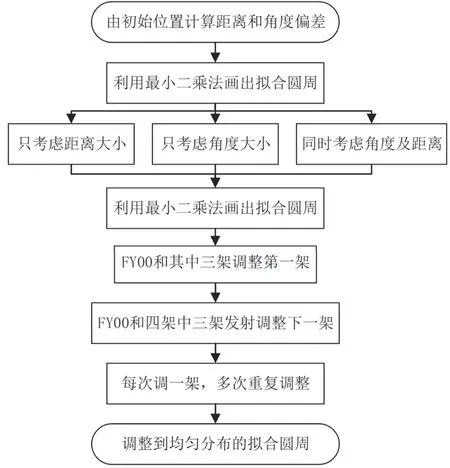
图4 调整方案
由单目标信号接收定位模型可知,在已知以圆心的FY00无人机为主发射器的情况下,至少需要再添加1架辅助发射信号的无人机,且任意2发射信号的无人机连线及其延长线不含有接收信号的目标无人机才可以对接收信号的目标无人机进行有效定位。在该结论的基础上,对结算过程进行推导,选择圆心无人机及任意3架圆周上的无人机为发射器,同时考虑目标在调整中的角度和距离,目标无人机沿着角度θ移动的距离如公式(32)所示。
根据上述单目标调整以及圆形阵的无人机定位模型的条件约束,每次取圆心无人机以及任意3架辅助发射信号无人机,对其余的无人机中任一目标进行调整,使其调整至圆周上,位置坐标位于拟合圆周表达式(公式(31)),再逐一对位置有偏差的无人机进行调整,在条件约束下的调整顺序具有任意性。
4 结语
针对无人机集群在遂行编队飞行时保持编队队形的问题,首先,该文采用TDOA定位法建立被动接收信号无人机的定位模型,对同一高度飞行的无人机进行有效定位。对同一高度飞行但初始位置略有偏差的无人机进行调整,使用MATLAB把初始位置存在偏差的无人机可视化,采用最小二乘法来拟合圆周,把位置偏差的无人机调整问题转化为点集调整到拟合圆周直线上的问题,再从题目限制条件出发来选择调整方案,根据定位模型来调整无人机的位置,使其均匀分布在圆周上。其次,给出锥形编队队形在题目限制条件下纯方位无源定位情形的无人机位置调整方案。为无人机有效定位和跟踪提供了一定的思路和方案,但是在实际飞行中仍然有很多影响因素,例如飞行速度、信号接收延迟、控制器的影响以及不同队形的调整等,拟合和计算误差也会影响定位的准确性,仍须进一步研究计算复杂度更小和模型更简单的方法,并将思路和方案应用到无人机跟踪领域。
