UbD理论下开展数学建模活动课程

宁德师范学院数理学院 蔡泉来 张 灏 卓梦彤 陈省江

随着时代的不断发展，数学应用更加受到重视，数学建模在基础教育阶段也越发受到重视。新课标将数学建模作为四大主线之一，并规定数学建模与数学探究活动课程不少于10 课时，希望通过数学建模课程培养学生用数学的眼光观察世界，提高学生数学思维能力和应用数学解决问题的能力。因此，开展数学建模活动课程是当前高中数学教学的一个热点。

本文以追求理解的教学设计理论（Understand by Desigen，以下简称“UbD理论”）为例，就如何开展数学建模活动课程进行研究与探索。在UbD理论中，以逆向教学设计为指导、削菠萝为例，构建数学建模活动课程的教学设计，为一线教师开展数学建模活动课程提供参考。

一、教学目标的界定

数学建模核心素养大概念与核心任务可以抽象概括为数学模型，在削菠萝数学建模活动课程中，学生如何从削菠萝实际情境中抽象出数学问题，并构建出数学模型就是本节课核心任务。

明确课程核心与大概念，下面从课程标准、学情分析和课程内容这三方面进一步明确削菠萝的课程目标。

从课标对高中数学建模主题模块要求上分析，新课标要求学生完成一次数学建模活动课程，在实际情境中经历数学建模活动的全过程，即发现问题、提出问题、分析问题、构建模型，确定参数、计算求解，检验结果、改进模型，最终解决实际问题，并在探究过程中用语言交流，汇报探究结果。所以在削菠萝课程目标设定时要凸显课标要求，让学生经历从提出数学问题到解决问题的过程，以及明确语言描述的目标要求。

从学情分析上，通过已有数学建模的相关研究与实际调查，学生对数学建模了解情况整体偏低，数学建模所需的相关能力普遍不足。基于上述学情，教师要培养学生从削菠萝中抽象出数学问题，并应用数学知识解决问题的能力。教师要合理对能力目标进行划分，避免目标过于集中学生无法应对，以增强学生自我效能感，从中体会数学与实际的联系，增强数学应用和创新意识。

综合上述，拟定本次削菠萝数学建模活动课程的教学目标如下：（1）学生能用数学的眼光观察削菠萝问题，能抽象出数学问题，会用数学语言表达。（2）经历数学建模活动的基本过程，正确构建数学模型解决问题，并积累数学建模活动经验。（3）通过数学建模活动课程，感悟数学与现实的关联，增强数学应用和创新意识。

二、教学评价设计

界定好削菠萝的课程目标之后，下一步要做的是依据理解的六侧面构建课程教学评价，包括评价内容设计与评价方式。依据UbD理论下理解六侧面对本课程目标进行分析得出，学生要做到如下几点：（1）能用口头语言解释数学建模内涵、数学参数的实际意义，明确削菠萝本质问题。（2）能用文字语言阐明削菠萝情境下的数学问题、数学情境的假设、函数模型的构建过程和数学建模步骤过程。（3）能应用相关的几何或其他数学知识解决问题，完整呈现削菠萝问题解决过程的方案，提交研究报告。（4）洞察削菠萝问题的其他解决思路，反思模型构建的其他方法，在已构建模型的基础上优化模型。（5）深入他人思考的立场，构建模型的出发点。（6）对数学建模课程进行自知，包括对建模过程进行自我评价、反思以及对探究结论的表述。

三、教学设计

明确了预期结果，讨论了如何设置、收集达到目标证据的评估工具，现阶段要全面考虑适合的教学活动。威金斯和麦克泰格在UbD理论中提出：WHERETO这7个元素是教学活动的核心，同时强调这7个元素仅作为分析工具，用于检查设计，不为如何构建设计提供过程。因此，本次教学活动设计在WHERETO原则上进行梳理整合，得出数学建模教学活动设计遵循以下几个原则。

（一）问题情境

为有效开展数学建模活动课程，实际情境的选择要根据学生已有的数学建模素养水平，尽可能拉近学生与实际之间的距离，激发学生的兴趣，体现H。

（二）探究性学习

跟随情境回答问题推进教学，这就是一种探究性学习，探究基本满足“探究—猜想—论证”的过程，体现W，E-1，E-2，T，O。教学中的探究往往伴随着问题串，问题串中的首要问题也就是基本问题，具有较大迁移性，问题串设计要层层递进，从原有或学生能接受旧知识出发。数学建模活动课程要在数学建模活动环节分设基本问题，不断引导学生进行思维迁移，推动环节小活动的完成进而完成完整的数学建模活动。

（三）自我总结与反思

学生经历课堂学习，回头总结和反思是一种居高临下对本节课的总结思考，体现W，E-1，R，T，O。这不仅体现在数学建模活动结题这个环节，在各个小环节中都可以进行适当总结，以便更好地进行下一步教学活动。在总结过程中，教师可以引导学生对数学建模探究过程进行总结，不仅对知识应用进行总结回顾，更是回忆当时的心理活动，对学习时所涉及的数学思想方法进行总结，以便下次有更好的认识与运用。

综上所述，设定关于削菠萝数学建模活动的教学活动内容如下：①观察资料，观看短视频与菠萝实物，诉说收获的信息。②从数学角度进行解释店员削菠萝的原因，让学生明确削菠萝选题的意义。③从削菠萝情境中提出待解决的数学问题，分小组思考和讨论解决问题的根本是什么。④小组讨论如何控制变量，创设数学情境。⑤小组讨论解决问题的方法，阐述解决问题的方法的同时对开题做一次小结。⑥以小组为单位构建出削菠萝的数学模型，并请小组上台展示自己建模的过程与结果。⑦在已构建模型基础上引导学生进一步优化模型，使其具有一般化，思考如果切入角度不同对模型是否有影响。⑧不同学生对各小组完成过程进行评价，交换意见，并总结解题环节。⑨回顾与思考，总结对削菠萝探究的体会、感受，诉说对数学建模的认识，提交研究报告。

四、总结与启示

依据UbD理论构建数学建模活动课程的教学策略，整理如表1所示，提出开展高中数学建模活动课程的教学设计框架，为开展高中数学建模活动课程提供新思路。

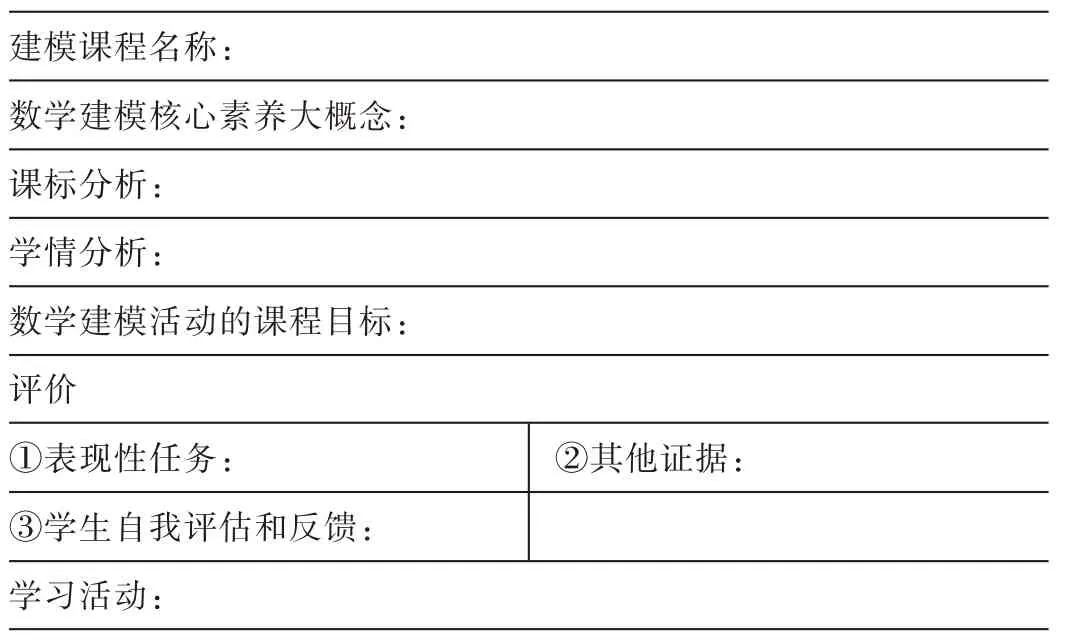
表1 数学建模活动教学设计框架

数学建模在UbD理论的基础上加以创新，以体现出数学建模的魅力。UbD理论以追求理解为宗旨，从课程目标出发进行逆向教学设计，教学过程逐步深入，符合学生身心发展特点，也满足将建模过程主动权交给学生，让学生体验建模过程，保证学生的主体地位，但最后还是提以下几点注意事项：（1）课题选择不仅要照顾学生现有的数学建模水平，还要与相应知识单元相结合，进行实现融会贯通，将数学建模与高中数学知识相联系以巩固学生对数学知识的理解应用。（2）评价方式的多样化，改变了过去教师单一评价，可以设计学生互评，自评等形式。（3）改变教学方式，以学生为主体，教师起引导作用，用大问题启发学生思考，讨论开展探究形式的数学建模活动课程。