基于排队论的智能快递柜格口定价策略
2022-03-24张力菠葛禄璐王赫鑫
张力菠,葛禄璐,王赫鑫
(1.南京航空航天大学 经济与管理学院, 江苏 南京 211106;2.北京航空航天大学 经济管理学院, 北京 100191)
2019年,我国快递业务总量达635.2亿件,同比增长25.3%,业务总收入7 497.8亿元,同比增长24.2%,连续六年位居世界第一[1]。巨大的快递包裹量和消费者对快递服务质量、时效性和个性化的高需求极大加剧了末端物流配送的压力,在此背景下,一种基于智能快递柜的新的配送模式应运而生。凭借24 h全天候自助服务、收取件方便、非直接接触等优势,智能快递柜可有效解决快递员与客户时间和空间的不一致问题,从而提高投递效率、降低配送成本,更可避免类似新冠疫情下的接触传染风险,因而日益受到物流、快递公司及客户的认可和青睐,势必迎来更广阔的发展空间。但是,其发展依赖于大量快递柜的投入和使用,基于快递柜供应商的角度,目前快递柜盈利模式相对单一,其收益主要来源于投递和广告业务,面临高投入低回报的压力[2]。为此,供应商往往会抬高快递柜服务定价或收取其他相关费用。相反,使用快递柜的小区物业及客户则认为供应商快递柜服务业务利润率并不低,如不延长免费使用时长等将停止使用快递柜[3]。快递柜供应商与小区/客户之所以发生上述冲突,除投递前是否征得客户同意等服务因素外,快递柜供应商的服务收益情况是主要根源之一。当前,我国快递柜服务业务总体上还处于起步阶段,研究快递柜供应商的收益及其影响因素,厘清服务定价机制,对快递柜业务的可持续发展具有重要意义。
智能快递柜业务的已有相关研究主要集中于以下方面。
1) 智能快递柜的优势分析。智能快递柜可以减少配送时间、降低投递失败率,是解决物流配送“最后一公里”问题的有效方法之一[4]。共享快递柜等接收箱有助于提升配送效率,适合人口密集和快递量较多的地方[5]。Kiousis等[6]、Ron Van Duin等[7]分别以雅典和阿姆斯特丹为例,研究表明快递柜有助于减少货运车辆的使用时间和里程,可作为一种新的替代配送模式,减轻对交通网络和环境的负担。
2) 盈利模式。Quak等[8]分析智能快递柜的商业模式及其财务可行性,表明正确的运营管理是快递柜供应商面临的主要挑战之一。王嘉琪等[9]认为智能快递柜业务的盈利模式不清晰,影响了大范围推广。
3) 服务质量及客户满意度。尚玉冰等[10]研究发现快递柜的收费、格口尺寸和数量、故障处理速度等是影响顾客满意度的主要因素。陈碎雷[11]采用因子分析方法研究智能快递柜服务质量的影响因素,并提出提升其服务质量的对策。Vakulenko等[12]研究快递柜带来的客户价值,给出快递柜供应商改善客户使用体验的依据。
4) 设计与选址等。Deutsch等[13]研究给定区域的地形和消费者需求情况下,如何设置快递柜的数量、尺寸大小及选址以使供应商收益最大。Pan等[14]采用人机工程方法,对大学智能快递柜的尺寸与布局进行优化设计,使其接收能力提高了89%。Faugère等[15]提出一种全渠道B2C物流环境下模块化智能储物柜的优化设计方法,以提升固定式快递柜的灵活性。
从已有研究看,智能快递柜格口定价及供应商收益问题的相关研究还相对不足,尤其快递柜格口服务价格应该如何设定?不同格口数量和定价对供应商收益有何影响?如果延长免费使用时长或不向客户收取超时费用,而仅向快递员或快递公司收取费用,供应商收益会如何变化?快递员使用快递柜后的成本-收益情况如何?这些问题还有待深入研究。鉴于智能快递柜主要提供“最后一公里”的末端配送服务,其与快递包裹构成一种排队服务系统,因此,本文采用排队论方法,刻画快递柜与快递包裹之间的服务运作流程,构建快递柜供应商的收益模型,探寻不同情景下快递柜格口的定价策略。
1 智能快递柜服务业务分析及假设条件
目前市面上不同应商提供的智能快递柜的格口尺寸各不相同,一般可分为小、中、大3种规格。表1列出当前主流品牌的一组智能快递柜中不同类型格口的数量,可以看出,大格口占比非常低,为研究方便,将大格口和中格口归为一类,统称为大格口。

表1 不同品牌智能快递柜的格口数量Table 1 The numbers of the lockers of intelligent express cabinets of different brands
对于快递员来说,一般可自由选择是否使用快递柜。快递员愿意使用快递柜主要是因为客户不在目的地,以及为了避免找寻目的地、上楼耗时、无效等待,从而减少配送距离和时间,增加自己单位时间内完成的配送快递数量;也有一部分快递员因害怕客户投诉服务不到位或不愿支付快递柜格口使用费而选择配送到客户目的位置。因此,在客户同意将包裹投递到快递柜的情况下,快递员使用快递柜的意愿在很大程度上取决于格口费用,如果使用快递柜带来的配送效率提升及机会成本减少高于使用成本,则会加强他们的使用愿意。
基于以上分析,特提出以下假设。
1) 某处场所只放置一组由一个主柜和多个副柜组成的快递柜,且快递柜只有大格口和小格口。
2) 只考虑送货上门和使用快递柜这两种配送方式,快递员不使用快递柜时,只能自己配送。
3) 大件快递和小件快递的配送成本相同。
4) 若使用快递柜格口的费用小于快递员自己送货上门的成本,快递员就一定会选择使用,且不考虑格口尺寸的限制。
5) 快递柜供应商的收益来源于快递员寄存收费和广告收入,不考虑寄件收益、超时收费和其他业务收益;不考虑供应商前期的投入成本,只考虑运营期间的费用。
2 智能快递柜供应商的收益模型
2.1 问题描述
除双十一、传统节日及其他特殊时期外,商场、学校、办公楼、小区等的固定位置的快递柜,每日平均到达的快递数量和到达的时间间隔变化并不大,其到达过程可视作泊松过程。因此,将每一个格口看成服务台,快递视作 “顾客”,一个快递从被快递员放入格口到被客户取出的时间就是服务时间。对于某一固定位置的快递柜,除特殊情况外,其每天平均收入的快递数量和每个快递的平均服务时间变化也不大,故格口对快递的服务时间可视为服从指数分布。
此外,到达快递柜的大件快递只能存入大格口中,而小件快递会优先选择小格口,当小格口已满时,快递员可以选择使用大格口。大件快递和小件快递的数量是相互独立且平均到达率一定,大格口和小格口的服务时间也相同,则智能快递柜的大格口和小格口可分成两个排队系统。当大格口或小格口被全部占用时,快递就无法进入,快递员会选择自己送货上门,这对排队系统来说是一种损失。因此,智能快递柜的大格口和小格口都可以看作是一个M/M/n/n损失制的排队系统。
设某处的一组快递柜有nb个大格口,ns个小格口,基于前面论述,将快递柜大格口记作M/M/nb/nb排队系统,小格口记作M/M/ns/ns排队系统。快递员自己配送一个快递的费用为Cm元,因为配送的距离、等待的时间等不同,每一个快递所需的费用是不同的。假设Cm是随机变量,概率密度函数f(Cm),概率分布函数为F(Cm)。智能快递柜的大格口价格为cb元,小格口价格为cs元,且cs≤cb。当格口收费小于自己配送的费用时,快递员使用快递柜配送。而且大件快递只能放入大格口中,小件快递优先选择小格口,如果小格口满了,则选择大格口。当cb≤Cm时,快递员愿意使用大格口;当cs≤Cm时,快递员愿意使用小格口。快递员的配送流程如图1所示。

图1 快递员的送货流程Figure 1 The delivery process of a courier
以1 d为单位时间,大件快递和小件快递的到达服从泊松过程,平均到达数量分别 δb、 δs。每个格口每天服务的快递数量,即服务强度为µ。快递柜供应商从屏幕和柜体上的广告获得的收益按照曝光次数来计算,即顾客每取一次快递,意味着能看到一次广告,供应商就能获得ca元的收益。快递柜的运维成本主要是电费、网络费和维护管理费用等,设快递柜的每个格口1 d的运营成本是c0元。
2.2 模型建立


供应商的日常利润来源于大、小格口系统的收益并扣除运营成本。大小格口的收益都取决于广告收费、各自的使用费用和服务的快递数量。所以供应商的利润为

3 数值实验及分析
3.1 供应商利润最大化时的格口价格
以我国某二线城市的一个约800户居民的小区为例,每天快递数为200个,其中大件和小件快递各100个;目前小区只有一组智能快递柜,其中大格口和小格口各为50个,快递柜的周转率为150%,即每个格口每天服务的快递数目为1.5个;快递员自己配送一个快递的费用服从均匀分布,且最小值为0,最大值为2;每个快递给供应商带来的广告收益为1元,每个格口1 d的运营成本为0.2元。相关参数的初始值如表2所示。

表2 相关参数的初值Table 2 Initial values of related parameters
最终计算得到该小区快递柜供应商的最大利润Vmax=195.63元,此时其他变量的结果值如表3所示,其中大、小格口的最优服务价格分别为0.79、0.63元/次;快递员使用快递柜可节约成本为每天36.81元。由此可以看出,在供应商利润达到最大值的时候,快递员使用快递柜也能够减少自身的机会成本。到达大格口排队系统的快递数量为64.14个,则实际进入到大格口的快递数量为64.14× (1-0.036)=61.83个;到达小格口排队系统的快递数量为68.50个,则实际进入小格口的快递数量为68.50× (1-0.060)=64.39个。

表3 供应商利润最大时相关变量的结果值Table 3 Some variable’s value under supplier's maximum profit
3.2 相关参数的影响
模型中相关参数在实际中是不确定的,不同参数值势必对计算结果产生影响。因此,为了厘清格口数量、快递平均到达数量、快递柜的服务强度、广告收益等参数与供应商最大利润、快递员可节约成本以及此时的最优格口价格的关系,继续基于3.1中的案例数据进行数值实验。
3.2.1 格口数量的影响
1) 大、小格口数量相等,总和变化。
从图2、图3的实验结果可以看出,随着格口数量的增多,供应商的最大利润呈现先快速增长然后缓慢回落的趋势。当大、小格口数量均为60个时,其最大利润达到最大值,但与大、小格口数量均为50个的情景相比并未提升很多。之后,随着格口数量的持续增多,最大利润开始缓慢下降。快递员的节约成本是先下降后升高至最高值保持不变,而且当大、小格口数量高于35个时,快递员获得的成本节约才变为正值。这就意味着,快递柜数量低于一定值时,快递员使用快递柜是亏本的。值得注意的是,当供应商最大利润保持在较高水平时,快递员的节约成本也比较理想。另外,由于随着格口数量的增加,供应商收益不断增长,因此,格口数量递增有助于带动格口最优价格的递减,小格口价格先于大格口价格降至最低水平,此后保持不变,为0.5元。

图2 大小格口数量相等,总和变化情景下,供应商最大利润及快递员节约成本Figure 2 The supplier's maximum profit and the courier's saved cost when the numbers of large locker and small locker are equal and the sum changes

图3 大小格口数量相等,总和变化情景下,大、小格口的最优价格Figure 3 The optimal prices of large lockers and small lockers when the numbers of large lockers and small lockers are equal and the sum changes
总体来看,当大、小格口数量达到50个后,再增加格口数量对供应商利润的提高并不明显,但依旧能在很大程度上影响格口的价格降低,从而减少快递员使用快递柜的费用。从供应商利益的角度来说,可以不必设置最优格口数量,但是考虑到快递员是价格敏感群体,即使增加格口数量不能够带来更多的收益,为了提高服务满意度,培养客户忠诚度,适当增加格口数量还是有一定的积极意义。
2) 大小格口数量比例变化,总和为120个从上面分析可知,大、小格口数量均为60个的时候,供应商最大利润达到最大。对比图2和图4可以看出,当大格口数量增加时,供应商最大利润、快递员节约成本的变化曲线与大、小格口数量相等时的变化曲线类似。不同之处在于前者的供应商最大利润和快递员节约成本的起始点都较高,且供应商最大利润到达最高点后保持不变。此外,从图5可以看出,大小格口数量比例变化对大格口最优价格的影响较大,而对小格口最优价格的影响很小,这跟情景1中大、小格口数量相等,总和变化的影响(见图3)有明显区别。

图4 大小格口数量变化,总和为120个情景下,供应商最大利润及快递员节约成本Figure 4 The supplier's maximum profit and the courier's saved cost when the proportion of large lockers and small lockers varies and the sum is 120

图5 大小格口数量比例变化,总和为120个情景下,大、小格口的最优价格Figure 5 The optimal prices of large lockers and small lockers when the proportion of large lockers and small lockers varies and the sum is 120
可以发现,较大的大格口数量有助于维持较高水平的供应商最大利润和快递员节约成本,同时格口的使用价格最低。但是,过多的大格口数量也会造成空间的浪费,所以供应商在投放快递柜之前应充分了解区域每日到达的快递的类型,以配置合理的不同规格大小格口的数量,不仅可以提高快递柜的服务水平,还能保持较高的业务收入。
3.2.2 快递数量的影响
1) 大件和小件快递数量相等,总和变化。从图6和图7的实验结果来看,快递数量达到一定水平后,数量越多,供应商的最大利润越高,但快递员的节约成本是先增加后减少,这是因为每一个快递都有配送成本,当快递数量过多、快递柜格口被全部占用时,快递员就无法通过使用快递柜降低配送成本。格口的最优价格起初都比较低,当大、小件快递数量达到10个时,都增加至0.5元,当快递数量超过约70时,格口价格开始增长,但大格口的最优价格先于小格口开始增长。

图6 大件和小件快递数量相等,总和变化情景下的供应商最大利润及快递员节约成本Figure 6 The supplier's maximum profit and the courier's saved cost when the numbers of large parcel and small parcel are equal and the sum changes
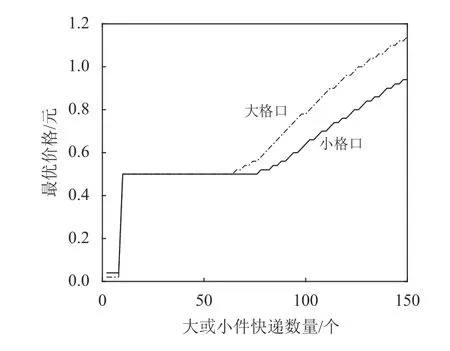
图7 大件和小件快递数量相等,总和变化情景下,大、小格口的最优价格Figure 7 The optimal prices of large lockers and small lockers when the numbers of large parcels and small parcels are equal and the sum changes
当快递到达数量超过快递柜服务能力时,供应商可能会提高格口价格,快递员为了尽可能多、更快地完成配送,依旧愿意支付费用,但如果使用费用超过配送效率提升带来的额外收益,快递员就会在效率和成本之间进行权衡,从而倾向于选择自己配送。因此,快递柜供应商有必要设置合适的格口数量,尽量实现快递柜的服务能力与需求的匹配。
2) 大件和小件快递数量变化,总和200个。
实验结果如图8和图9所示,随着快递件中大件快递数量的递增,供应商最大利润和快递员节约成本从最大值呈现缓慢减少的趋势,当大快递件超过100个之后,减势明显。大体来看,大、小格口的最优价格起初相差无几并保持不变,当大件数量超过60个后,大格口的最优价格不断增加,而小格口的最优价格下降到0.5元后保持不变。

图8 大件和小件快递数量变化,总和200个情景下的供应商最大利润及快递员节约成本Figure 8 The supplier's maximum profit and the courier's saved cost when the proportion of large parcels and small parcels varies and the sum is 200

图9 大件和小件快递数量变化,总和200个情景下大、小格口的最优价格Figure 9 The optimal prices of large lockers and small lockers when the proportion of large parcels and small parcels varies and the sum is 200
由于大格口的使用费高于小格口,所以当大件快递较少时,快递员可以获得较高的成本节约。大件快递的数量过多时会加剧大格口的需求缺口,从而使大格口最优价格升高,而小格口价格降低;当大件快递数量占比超过一定比例时,小格口因为无法存入大件快递,其最优价格并不受影响,这样既造成快递的流失又使得小格口出现闲置,供应商最大利润和快递员节约成本也因此而受到影响。
3.2.3 服务强度的影响
服务强度即快递柜的周转率,也就是每个格口每天服务的快递数量。从图10和图11可以看出,随着服务强度的增加,供应商最大利润呈现先大幅增长然后放缓的趋势,当服务强度超过2后,最大利润几乎不变。快递员节约成本的变化趋势相对复杂一点,在服务强度小于0.5时,节约成本逐渐减少;服务强度高于0.5后,节约成本才逐渐增加至最大值后保持不变,最终与供应商最大利润变化趋势基本保持一致。此外,大、小格口的最优价格随服务强度的增加而减小,当服务强度小于2时,小格口的最优价格比大格口提前进入稳定阶段,大格口的最优价格随后也稳定在最低水平。

图10 不同服务强度情景下的供应商最大利润及快递员节约成本Figure 10 The supplier's maximum profit and the courier's saved cost under different service intensities

图11 不同服务强度情景下大、小格口的最优价格Figure 11 The optimal prices of large lockers and small lockers under different service intensities
3.2.4 广告收益的影响
随着快递带来的广告收益增加,供应商的最大利润呈现近似线性的增加趋势,而且增速可观。相比之下,对应的快递员节约成本的增长缓慢得多(如图12)。此外,广告收益的增加使得大、小格口的最优价格总体上都呈下降趋势,而且小格口的最优价格对广告收益变化的反应要大于大格口的最优价格,下降幅度明显大于大格口(如图13)。

图12 不同广告收益情景下的供应商最大利润及快递员节约成本Figure 12 The supplier's maximum profit and the courier's saved cost under different advertising revenues

图13 不同广告收益情景下大、小格口的最优价格Figure 13 The optimal prices of large lockers and small lockers under different advertising revenues
当供应商的广告收入较高时,供应商就有可能降低格口的使用价格,但仍能维持较高的利润。由于大格口对小格口而言具有替代性,其使用价格变化相对稳定。所以快递柜供应商应积极进行广告招租,并不断探寻其他盈利模式,相关业务收益增加时就可以适当降低投递业务收入在总收入中所占的比重,从而提升快递员和用户使用快递柜的意愿。
4 结论
针对快递行业中快递柜格口服务价格及配置格口数量如何合理设定的现实问题,本文采用排队论方法,将快递柜大、小格口服务系统视为M/M/n/n损失制排队系统,结合快递员使用快递柜派件的流程,构建快递柜供应商的收益模型,探讨供应商利润最大时的格口价格以及相关参数对供应商和快递员收益及格口价格的影响。结果显示,大小格口数量及总数量、快递数量、快递柜服务强度、广告收益对快递柜供应商和快递员的收益及格口价格影响明显,但其影响并不是简单的线性关系。
1) 格口数量、服务强度、广告收益对供应商的收益总体上呈正向影响,而对格口价格主要呈负向影响,使其逐渐趋于0.4 ~ 0.68元/次,这跟目前市面上0.3 ~ 0.6元/次的价格相差不大。但这是未考虑快递柜硬件成本(主柜、副柜、监控及雨棚等)、线路改造及安装成本、进场费及租金等费用得到的实验结果。
2) 在不同的格口数量、快递柜服务强度和广告收益情景下,快递员的成本节约收益呈先降后升或缓慢增长态势,且大小和变化幅度也远小于供应商收益;而过少或过低的快递数量都会影响快递员使用快递柜获得更多成本节约收益。这从快递员角度说明,需要设置与服务区域内快递需求相匹配的快递柜格口数量,以免造成格口浪费或服务压力。
本文研究可为快递柜格口价格制定及快递柜业务发展提供参考。鉴于发展及环境条件的变化,后续研究可进一步考虑多品牌快递柜供应商竞争情况下快递柜的布局规划、定价及主体收益等问题。
(责任编辑: 郑穗华)
