需求可拆分的无人机与卡车协同路径优化问题

李妍峰，李 佳，向 婷

(西南交通大学 1.经济管理学院；2.服务科学与创新四川省重点实验室，四川 成都 610031)

随着科技的进步与发展，无人机不仅应用在军事方面，在民用物流服务方面也得到广泛应用。无人机灵活、快速的特点为提升物流效率带来很大空间。许多电商及物流企业相继展开了无人机项目，如顺丰、亚马逊、谷歌、DHL等[1]。但同时无人机也具有载重能力小、续航时间短等缺点，在实际配送中往往需要与卡车协同配送，发挥二者的优势。

近几年来，无人机与卡车协同配送路径优化问题引起国内外学者的广泛研究。不同于经典车辆路径问题(vehicle routing problem，VRP)，引入无人机后，两种访问方式结合的复杂路径关系使问题建模与求解的难度增大[2]。Murray等[1]最早提出无人机协助包裹递送的旅行商问题(the flying sidekick traveling salesman problem，FSTSP)，引起学者们的关注。随后研究从载有无人机的旅行商问题(traveling salesman problem with drone，TSPD)[1-7]进一步拓展到载有无人机的车辆路径问题(vehicle routing problem with drone，VRPD)[8-14]。目前文献对于VRPD问题研究主要从以下几个方面考虑。在问题优化目标的设置上，大多数研究以最小化完成配送的时间为目标[1,3-4,6,9-10,12,14]。Chang等[7]则将目标函数设置为最小化总配送时间。Wang等[8]、Schermer等[11]和Pugliese等[13]提出最小化卡车与无人机运输成本。Ha等[2]提出以最小化运输成本和等待成本为目标。在无人机单次可访问顾客的数量设置方面，由于无人机载重量较小，大多数文献考虑无人机一次只能访问一个顾客点，只有Wang等[8]和Ham[14]考虑在不超过载重的情形下，无人机单次可访问多个顾客点。在可供使用的卡车与无人机数目方面，针对TSPD问题，Murray等[1]、Ha等[2]、Yurek等[3]及Ponza[4]提出一辆卡车只能携载一架无人机；Carlsson等[5]、Boysen等[6]与Chang等[7]考虑一辆卡车可携载多架无人机的情形。针对VRPD问题，可同时使用多辆卡车用于配送，卡车的承载力又分为每辆车只携载一架无人机[9,12-13]及每辆卡车可载多架无人机[8,10-11,14]的情形。在求解算法方面，除Wang等[8]设计精确算法求解外，其余文献均设计启发式算法，在生成初始解后采取一些优化策略进一步提升解的质量。

目前在VRPD的研究中，未从顾客点的分布特征考虑。例如在一些边远地区，顾客点分布相对稀疏，交通不便和卡车较大的平均运输成本为卡车配送服务带来困难。京东曾指出无人机快递服务可用于解决农村地区的快递配送问题[15]。基于此背景，本文根据顾客点的分布特征将顾客点分为仅由无人机配送和由卡车与无人机协同配送两类。另外，已有研究均仅考虑每个顾客由一架无人机访问的情形[1-14]，而在实际中，由于无人机的载重量较小，单架无人机的载重量很难完全满足顾客需要，因此本文考虑顾客需求可拆分属性，当需求量大于无人机载重时，允许包裹拆分，且每个顾客可被无人机访问多次。在上述问题特性的基础上，以最小化运输成本和使用卡车的人力成本为目标，考虑卡车载重量、无人机载重量和续航时间、需求拆分比例和路径可行性等约束，建立混合整数规划模型，并根据问题属性设计一种改进变邻域搜索算法，对不同算例规模下的问题进行数值实验验证算法的求解性能。

1 问题描述及模型建立

1.1 问题描述

本文考虑基于顾客点的分布特征的无人机与卡车分区域协同配送问题。根据客户需求的分布，将配送区域分为需求稀疏区域和需求密集区域。需求稀疏区域的客户由于距离配送中心较远且运输成本较大，安排无人机进行服务。而在需求密集地区，无人机与卡车两种配送方式均可采用。对应的顾客点也可分为两类：卡车与无人机二者均可访问的顾客点(第1类顾客点)；只能由无人机访问的顾客点(第2类顾客点)。

卡车携载无人机从配送中心出发去服务两类顾客点，配送任务结束后回到中心，且在途中承担发送和接收无人机的服务。由于无人机载重量较小，当需求超出无人机载重时，允许拆分包裹，多次访问该顾客。其中，对于第1类顾客点：当需求重量不超过无人机载重量时，采用两种配送方式中的任意一种；当需求重量超过无人机载重量时，或不拆分采用卡车配送，或拆分后采用无人机多次配送。对于第2类顾客点，只采用无人机配送方式，当需求量超出无人机载重，则拆分后配送。本文提出的需求可拆分的无人机与车辆协同路径问题(split delivery vehicle routing problem with drone, SDVRPD)还具有如下特点。

1) 要求所有顾客点均被访问；

2) 每辆车最多承载一架无人机；

3) 无人机一次只能访问一个顾客，但每架无人机可以多次访问顾客；

4) 在运输过程中，随车无人机只能从其搭载车辆出发并回到该车辆；

5) 无人机的起飞点与着陆点不同；

6) 在无人机访问顾客时，允许拆分包裹，多次服务，无人机每次携带的包裹重量不能超过其载重；

7) 每个顾客的需求只能由卡车与无人机其中一种配送方式服务。

图1是本文卡车与无人机协同配送问题的示例，共有3辆卡车提供服务。0点表示配送中心，1 ～6，9 ～ 12，15 ～ 17点表示第1类点，其中1 ～ 5，9 ～12，15 ～ 17点由卡车访问，6、13点由无人机访问；7 ～ 8、14、18点表示第2类点，7、14点无人机单次配送即可满足，8、18点需求拆分，无人机两次访问满足。

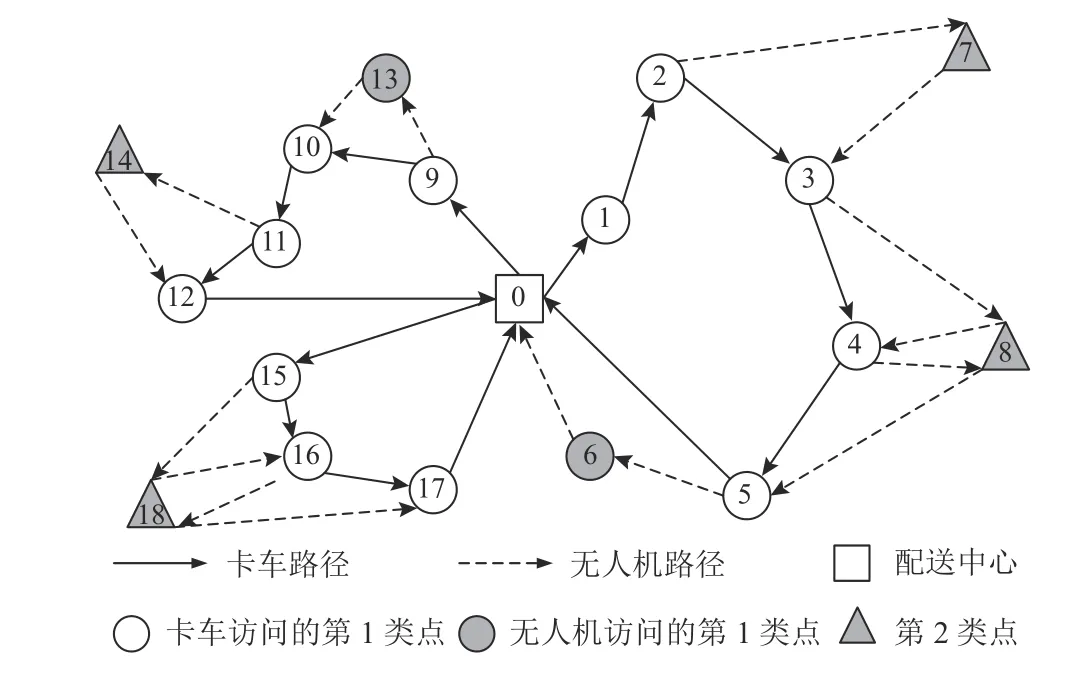
图1 问题示例Figure 1 Example of problem

1.2 符号说明

1.3 模型建立

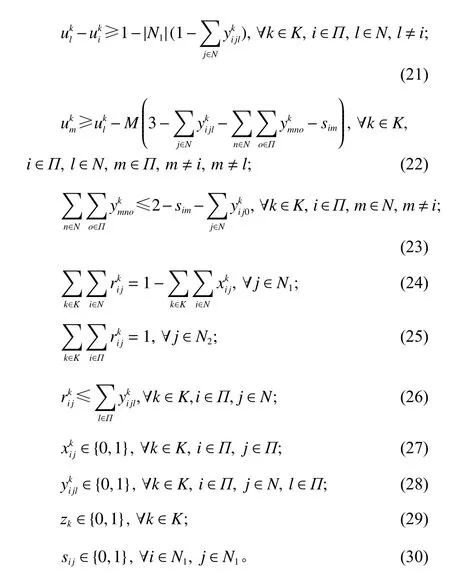
目标函数(1)是最小化总成本，包括使用卡车的人力成本以及卡车与无人机的行驶成本；约束(2)表示对于车辆不可达的客户点，只能由无人机进行配送；约束(3)表示对配送方式无要求的顾客，车辆与无人机送货均可；约束(4)表示每辆卡车访问顾客的需求量与其承载无人机的访问顾客需求量之和不能超过卡车最大载重量；约束(5)表示无人机每次服务顾客携带的包裹重量不超过无人机的载重量；约束(6)表示无人机飞行时长不能超过其最大续航时间；约束(7)表示对第1类顾客点而言，若卡车访问该点，则必须从该点离开到达其他点；约束(8)和(9)表示卡车从配送中心出发，服务后返回配送中心；约束(10)和(11)表示无人机离开与返回卡车的点必须有卡车访问以发送和接收无人机；约束(12)表示若第1类点由卡车访问，则无需无人机访问；约束(13)表示只有使用卡车，对应搭载的无人机才可能有访问路线；约束(14)表示若携载无人机则必有航行路径，无携载无人机则没有；约束(15) ～ (18)为卡车路径的避免子环约束，由于配送中心既作为出发点又作为终止点，本文没有设置两个集合分别表示出发与到达[1-11]，而将0点单独考虑；约束(19)和(20)为两变量的转换关系；约束(21)保证在卡车访问顺序中访问无人机起飞点要先于着陆点；约束(22)和(23)表示无人机访问的先后顺序，不可交叉进行：针对同一架无人机的两次访问，若一次访问的起飞点访问次序后于另一次访问的起飞点，则其访问次序也后于另一次访问的着陆点；约束(24) ～ (26)表示无人机携带重量比例的关系：针对所有由无人机访问的顾客点，分配比例之和为1；约束(27) ～ (30)表示变量为0-1决策变量。

2 算法设计

Murray等[1]指出FSTSP是NP-hard问题，本文所提出的SDVRPD是该问题的扩展，因此也是NP-hard问题。精确算法只能求解小规模问题，对于大规模问题求解非常困难。因此，本文设计一种改进的变邻域搜索算法(improved variable neighborhood search,IVNS)来求解本问题。在已有文献中，变邻域搜索对于求解路径优化问题表现出很好的性能[16-19]。结合问题特性，在初始解产生上，首先针对无人机载重量超出顾客需求的第2类顾客点进行拆分，构造虚拟顾客点，然后安排所有顾客点由卡车访问，采用贪心策略将第2类顾客点改为由无人机访问，从而得到变邻域搜索的初始解；根据模型特征，本文设计6种适用于问题的邻域算子用于邻域搜索和扰动；最后，设计两种改进算子进一步提升解的质量。本文所设计算法的框架如表1所示。

表1 改进变邻域搜索算法的整体框架Table 1 The overall framework of IVNS

2.1 预处理

在本问题中，由于第2类顾客只能采用无人机方式进行配送且无人机载重量较小，因此允许拆分配送。针对这一特性，编码前首先进行预处理。将第2类顾客点中超出无人机载重量的顾客拆分为n个顾客(n是采用无人机访问方式下客户需求的最小拆分数)，即虚拟n-1个顾客点，虚拟顾客点的坐标与原坐标相同。在需求的分配上，根据模型中的随机化设置，将总需求量随机分配给这n个顾客，各自的需求都不超过最大载重量。具体步骤如表2所示。

表2 预处理的操作步骤Table 2 Operation steps of encoding preprocessing

2.2 初始解的构造

在Kitjacharoenchai等[9]的研究中，所有顾客均可采用卡车和无人机两种方式访问，初始解通过安排所有顾客由卡车访问来产生，由于本问题要求第2类点必须由无人机进行访问，这种方式并不完全适用。结合问题特征，设计新的初始解产生方式，具体流程如下。

Step 1 所有顾客均由车辆访问，随机生成路径序列，若卡车载重量无法满足则使用下一辆车，设使用车数为K，每辆车的路径为Rk(k=1-K)。

Step 2 初始化：k=1。

Step 3 将Rk中第2类顾客点从中剔除，放入集合Fk中，剩余包括第1类点的序列Rk′。

Step 4 将集合Fk中的顾客点依次插入序列Rk′中，插入方法采用贪心策略：每点优先被插入到运输成本最低的位置，同时需考虑该种插入方式是否超出无人机续航时间，若超出则选择成本次低位置，重新考虑续航约束，直至Fk中的所有点被插入完成，k=k+1。

Step 5 若k≤K，转向Step 3；否则结束，从而得到初始解。

2.3 邻域算子及算法框架

变邻域搜索利用不同的邻域结构进行交替搜索，在集中性和疏散性之间达到很好的平衡。邻域算子用来从当前解中产生新解，本文设计多种满足问题特性的邻域结构用于变邻域搜索。在执行所有的邻域操作时，都要考虑执行操作后，更改访问路径的无人机访问的顾客点是否超出无人机续航时间，若超出则不执行该操作，从而避免不可行情况。在下降算法部分共采用6种邻域结构提升解的质量，包括4种线路内邻域算子(见图2)和2种线路间邻域算子(见图3)。扰动部分采用5种邻域结构，包括更换无人机起止点、子序列逆序、无人机两点交换以及将卡车两点交换拆分为相邻两点交换和不相邻交换。

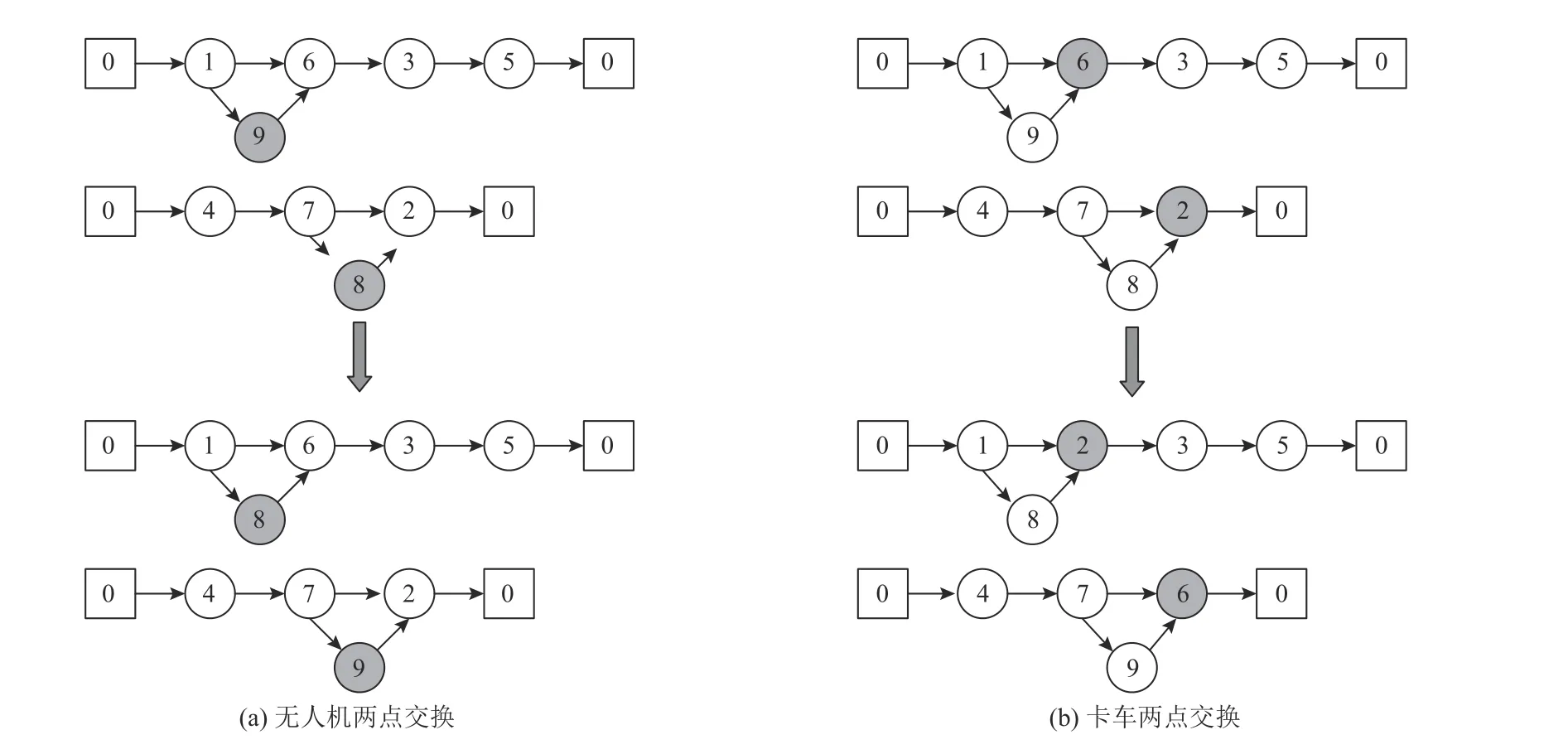
图3 线路间邻域算子Figure 3 Neighborhood operator between lines

2.3.1 邻域算子

线路内邻域算子如下所示。

1) 更换无人机起止点(如图2(a))：改变无人机的原插入位置到新的位置。

2) 子序列逆序(如图2(b))：在卡车路径中随机选择一条子路径，将该序列逆序，子序列两端相关联的由无人机访问的顾客点更改断开的单侧起飞点或着陆点，内侧无人机访问的顾客点更换起止点的前后关系。

3) 无人机两点交换（如图2(c))：随机选择两个无人机访问的顾客点，交换位置。

4) 卡车两点交换（如图2(d))：随机选择两卡车访问的顾客点交换位置，相关联的无人机访问的顾客点的起止点随之改变。

线路间邻域算子如下所示。

1) 无人机两点交换(如图3(a))：分别在两条不同卡车路径中选择一点，交换位置。

2) 卡车两点交换(如图3(b))：分别在两条搭载不同卡车的无人机路径中选择一点，交换位置，相关联的无人机访问的顾客点的起止点随之改变。

2.3.2 邻域搜索算法框架

邻域搜索算法框架如表3所示。

表3 邻域搜索算法框架Table 3 The flow of the neighborhood search algorithm

2.4 进一步改进

在初始解产生过程中，由无人机访问的顾客点安排在卡车访问路径中相邻的两点间插入，且在2.3节中设计的邻域算子中也保持这一特点。为了进一步优化路径，设计一个起止点延伸的算子，若无人机航行起点与终点不相邻时能使降低成本，则执行该操作。另外，在邻域搜索的过程中，因为第2类顾客点只能采用无人机进行访问，所以优先满足第2类顾客点使用无人机访问，第1类顾客点则全部由卡车访问。事实上，针对第1类顾客点，采用无人机访问方式很大程度能减少成本，因此设计卡车点改为无人机点这一算子。两种算子操作如下。

1)起止点延伸(如图4(a))：将无人机所访问顾客点的出发点或着陆点向外延伸，跨点访问。

2)卡车点改为无人机点(如图4(b))：将由卡车访问的顾客点改为由无人机访问，将该点从原卡车路径中删除，若需求量小于无人机载重，寻找成本最小位置插入；若需求量大于无人机载重，将该点拆分后分别寻找成本最小位置插入。

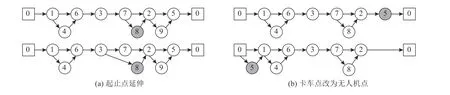
图4 改进邻域算子Figure 4 Improved neighborhood operator

3 数值实验

以下3.1节通过小规模算例对问题特性进行分析(采用ILOG Cplex12.9对模型进行求解)，3.2节对构造的不同规模算例进行数值实验，通过与Cplex的求解结果对比，对改进的变邻域算法的效率进行验证。算法采用C#语言进行编程实现，实验均在i5-5250CPU，主频1.6 GHz，内存4 G的PC上进行。

3.1 参数分析

本节构造包含7个第1类顾客点和3个第2类顾客点的算例。参考文献[12]的数据，参数设置如下。C=1 300 kg，C′= 5 kg，v= 50 km/h，T= 1，cT= 0.6 元/km，cD= 10%·cT= 0.06 元/km，cF= 50 元/辆。通过对卡车载重C、无人机载重C′和无人机运输成本cD的灵敏度分析对问题特性进行分析。顾客点的坐标及需求量如表4所示。

表4 顾客点信息Table 4 Customer information

3.1.1 卡车载重C分析

表5给出C=30，60，90时，传统的卡车单独送货(VRP)和无人机与卡车协同送货(SDVRPD)两种情况下求解的目标函数值、使用卡车数和访问路径，以及SDVRPD相比VRP目标函数值的节省比(%)。两种情况下的顾客点信息均采用表1数据，其中，VRP不区分顾客点类别，1 ～ 10点全部由卡车访问。

表5 不同C 下的求解结果Table 5 Solution results under different C

从表5中可以看出，在不同的卡车载重量下，SDVRPD和VRP所用车数相同，但访问路径不同，甚至每条路径的顾客分配也不同，这主要由于无人机与卡车单位运输成本差异较大，不同路径下无人机访问节省的成本更大，可以在抵消卡车更换路径增加的成本后仍使成本减少。另外，随着卡车载重量的增大，使用卡车数目逐渐减少，目标函数值随之减少，节省比例逐渐增加，从4.82%增加到9.5%。

3.1.2 无人机载重C′分析

表6给出了C′=3, 4, 5, 6, 7, 8时的目标函数值、第2类顾客点的拆分点数、访问路径以及相比VRP目标函数值的节省比(%)。图5给出了目标函数值随无人机载重C′的变化曲线。

由表6可知，在不同载重下，卡车访问路径的顺序变化不大，主要影响的是无人机的访问路径。随着C′的增大，无人机在单次访问过程中能够满足更大需求量，第2类顾客点中需拆分的顾客数随之减少，并且拆分点生成的虚拟顾客个数也会减少，从而减少访问第2类顾客的运输成本；另外，增大无人机载重量使原来无法由无人机访问的第1类顾客可被访问，减少卡车访问第1类顾客的运输成本。以上两方面导致目标函数值的减少，从而使相比VRP的节省比例逐渐增大，从C′=3对应的0.64%增长到C′=8情形下的11.42% (如图5所示)。结果表明，无人机的载重量越大，节省的运输成本越大，将无人机引入配送越有利。

图5 C′=3, 4, 5, 6, 7, 8的相关折线图Figure 5 Related line chart of differentC′

表6 不同C ′下的求解结果Table 6 Solution results under differentC′

3.1.3 无人机单位运输成本cD分析

表7给出了无人机单位运输成本cD取不同值时的目标函数值、第1类顾客点中由无人机访问的数目、访问路径以及相比VRP目标函数值的节省比(%)。图6给出了目标函数值和节省比随cD的变化曲线。

表7 不同c D下的求解结果Table 7 Solution results under differentcD

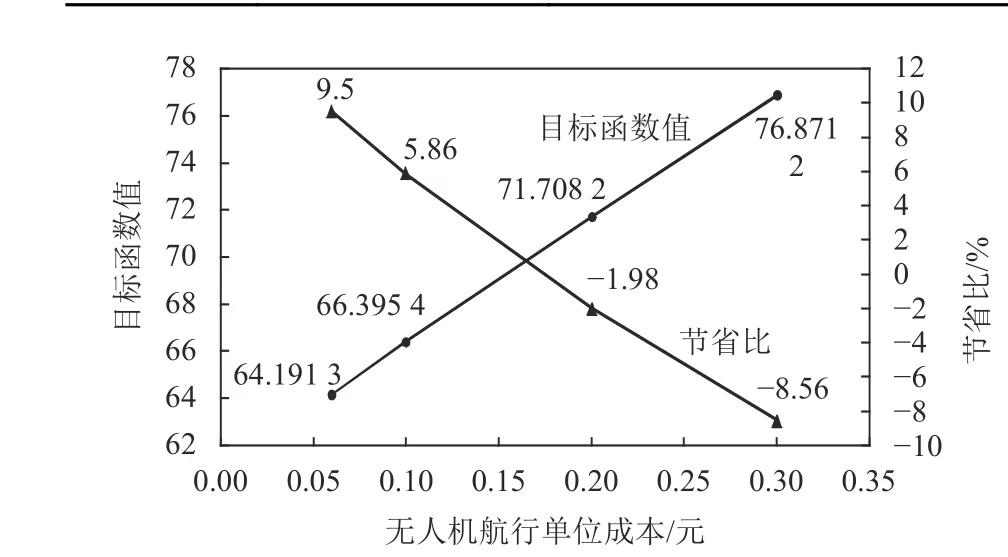
图6 cD=0.06, 0.1, 0.2, 0.3的相关折线图Figure 6 Related line chart of different cD

如表7所示，当cD=0.06，0.1时，访问路径完全相同，此时有2个第1类顾客点由无人机访问，目标函数的不同主要由无人机单位运输成本所致。随着cD逐渐增大，原本由无人机访问的第1类顾客点变为由卡车访问，因为无人机成本的增大导致采用无人机访问方式已经无法节省成本，并且目标函数值逐渐增大，相比VRP的节省比例为负值(如图6)，表明在较大无人机单位运输成本下，在VRP基础上引入无人机反而会增加总成本。相应地，在无人机技术中进一步减小无人机单位运输成本对降低物流成本有很大意义。

3.2 算法性能分析

3.2.1 算例产生及参数设置

由于尚无针对本问题的标准算例，本文采用随机方式生成顾客位置，算例规模表示为|N|(|N1|+|N2|)。基于问题特性，具体产生方式如下。在二维平面上构造两个中心相同的正方形，边长分别为20 km和10 km，两正方形的重叠部分为区域1，未重叠部分为区域2。在区域1内随机生成|N1|+1个点，第1个点作为配送中心，其余点作为第1类顾客点；在区域2随机生成 |N2|个点作为第2类顾客点。顾客需求同样采用随机生成方式，第1类顾客点设置为[0, 40]的1位小数，第2类点设置为[0, 15]的1位小数。参考文献[12]数据，问题参数设置为C= 1 300 kg，C′ = 5 kg，v= 50 km/h，T= 1，cT= 0.6 元/km，cD= 10%·cT=0.06 元/km，cF= 50 元/辆。

3.2.2 算例测试及结果

为测试本文所设计改进变邻域搜索算法的求解质量，本节将改进变邻域搜索算法结果与精确算法进行对比。令无人机载重量C′为5 kg，无人机的单位运输成本cD为0.06元。设置目标数目|N|(|N1|+|N2|)分别为10(7+3)、20(14+6)、30(20+10)、50(35+15)、100(70+30)、200(140+60)等几种规模进行求解，为表明一般性，同等规模下，选取5组算例。表5给出不同规模算例下使用的卡车数目以及Cplex的求解结果，包括下界(LB)、上界(UB)以及上下界间的偏差值(Gap%)。求解中设置最大求解时间为7 200 s。同时表8还给出改进变领域搜索算法的求解结果，包括计算20次的平均目标函数值(Avg.obj)、平均gap值(Avg.Gap%=(Avg.obj-LB)/LB×100%)、最好解的目标函数值(Best.obj)、最好解的gap值(Best.Gap%=(Best.obj-LB)/LB×100%)以及平均求解时间(Time)。另外，表8还给出改进变邻域搜索算法的相对偏差值(Related Gap%=(Avg.obj-Best.obj)/Best.obj×100%)，用来衡量改进变邻域搜索算法求解的稳定性。

从表8中可以看出，当|N|=10时，Cplex在3 s内即可求得最优解；当|N|=20时，在210 s内可以得到最优解。随着问题规模扩大，当|N|=30时，只有一组算例用时4 870 s求得最优解，其余4组在7 200 s内只能求得可行解，且Gap值较大(30%左右)。随着问题规模进一步扩大，当|N|=50乃至更大数值时，Cplex在7 200 s内无法获得可行解。以上结果表明，精确算法能够较快地求解到小规模算例的最优解，但求解较大规模问题时存在很大局限性。

表8 改进变邻域搜索算法性能比较Table 8 Performance comparison of improved variable neighborhood search algorithm

由表8还可知，本文设计的改进变邻域搜索算法在本节设置的所有算例规模下的求解时间均在1 s内，在时间上相比Cplex具有很大优势，当|N|=10, 20时，除第10组算例外，改进变邻域搜索算法求得的最好解的目标函数值(Best.obj)均与精确算法的求解结果相同。当|N|=30时，改进变邻域搜索算法在极短时间内求得解的Gap值在4%以内，说明改进变邻域搜索算法求解效果很好，在不到1 s的时间内求解结果优于Cplex在7 200 s内求解的结果。当|N|=50, 100,200时，Cplex在7 200 s内已无法求得可行解，而改进变邻域搜索算法在1 s内求得可行解。另一方面，改进变邻域搜索算法在不同算例规模下的最好解与平均解的相对误差值(related gap)都比较小，在|N|=10, 20, 30等算例规模下相对误差值小于2%，在更大规模下相对误差值也稳定在3%内，充分说明改进变邻域搜索算法求解的稳定性。

4 结论

本文研究了一类需求可拆分的无人机与卡车协同路径优化问题。考虑到需求稀疏地区交通不便和卡车较大的平均运输成本，结合需求客户点的分布特征将配送方式分为两部分：需求密集地区的客户由卡车和无人机两种方式协同配送；需求稀疏地区的客户只能由无人机进行配送。另外，由于无人机载重小，引入需求可拆分特性，允许顾客多次访问。结合上述问题特性，考虑卡车载重量、无人机载重量和续航时间、需求拆分比例和路径可行性等约束，以最小化运输成本和使用卡车的人力成本建立混合整数规划模型，并设计一种改进变邻域搜索算法进行求解。小规模算例下分析问题特性得出：提高无人机载重量可有效减少需要拆分包裹的顾客数以及单顾客点的拆分次数，从而很大程度减少运输成本；降低无人机单位运输成本可以进一步增大卡车与无人机的成本差异，提高无人机服务率，进而降低物流成本。在多个不同算例规模的数值实验中，测试了改进变邻域搜索算法的性能。结果表明，在极短的时间内改进变邻域搜索算法能够求解更大规模的问题，并且求解质量较好，算法稳定性很高。后续研究可考虑动态需求下的路径优化问题。